【高频易错题汇编】19.3 课题学习 选择方案 (含解析)
文档属性
| 名称 | 【高频易错题汇编】19.3 课题学习 选择方案 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 667.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 12:53:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
19.3 课题学习 选择方案 高频易错题集
一.选择题(共10小题)
1.某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q(升)与流出时间t(分钟)的函数关系式为( )
A.20﹣0.2t B.Q=20﹣0.2t(t≥0)
C.Q=20﹣0.2t D.Q=20﹣0.2t(0≤t≤100)
2.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
3.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
4.一条公路沿线有A,B,C三个站点,甲、乙两车分别从A,B站点同时出发,匀速驶达C站.设甲、乙两车行驶xh后,与B站的距离分别为y1km,y2km.y1,y2与x的函数关系如图,则两车相遇的时间是( )
A.20min B.30min C.60min D.80min
5.横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是公里/分;(2)乙在冲刺阶段的速度公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
A.1 B.2 C.3 D.4
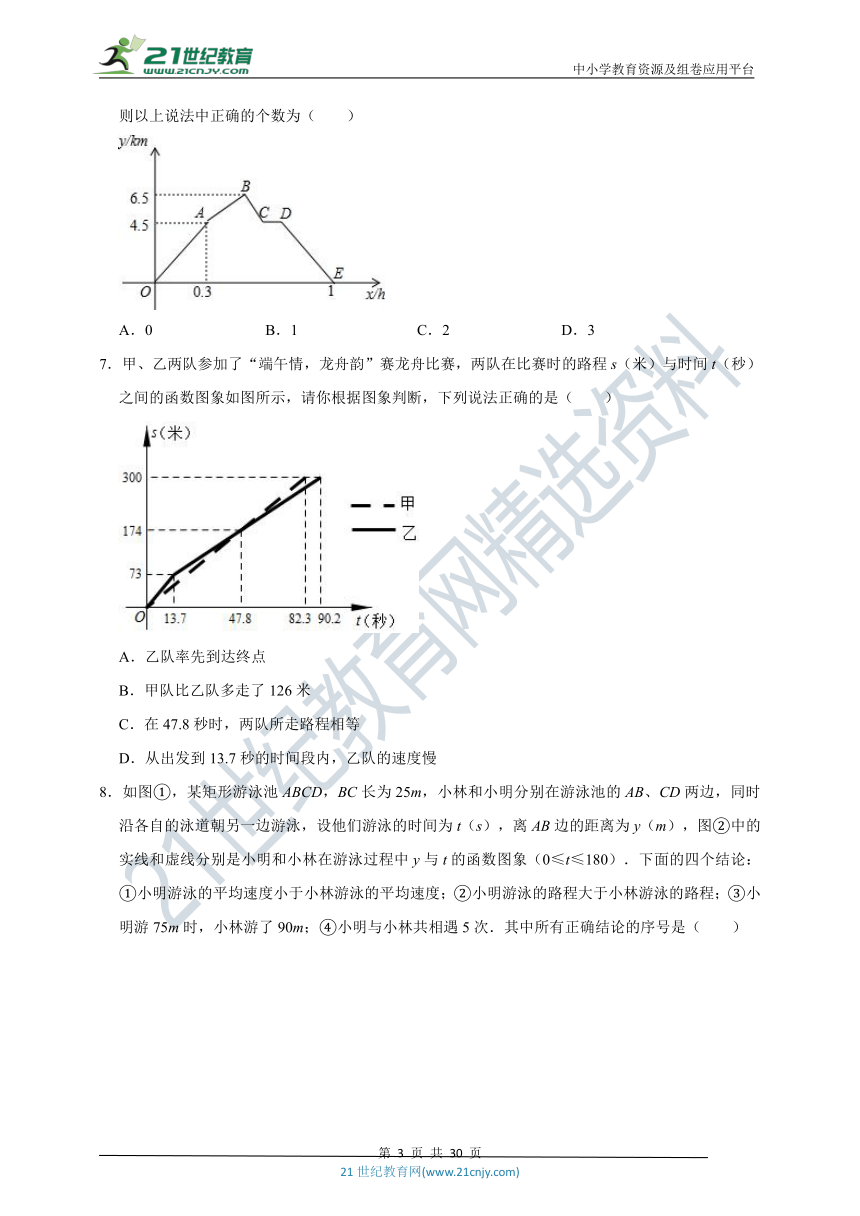
6.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
7.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
8.如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的路程大于小林游泳的路程;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中所有正确结论的序号是( )
A.①② B.①③ C.②④ D.③④
9.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=3;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共5小题)
11.若汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,则S与t的函数关系式为 .
12.两港相距640千米,轮船以15千米/时的速度航行,t小时后剩下的距离y与t的函数关系式为 .
13.“渝黔高速铁路”即将在2017年底通车,通车后,重庆到贵阳、广州等地的时间将大大缩短.9月初,铁路局组织甲、乙两种列车在该铁路上进行试验运行,现两种列车同时从重庆出发,以各自速度匀速向A地行驶,乙列车到达A地后停止,甲列车到达A地停留20分钟后,再按原路以另一速度匀速返回重庆,已知两种列车分别距A地的路程y(km)与时间x(h)之间的函数图象如图所示.当乙列车到达A地时,则甲列车距离重庆 km.
14.2018年10月24日,世界上最长的港珠澳大桥正式通车,香港口岸途径西人工岛到达澳门口岸.五一期间小辉与小亮两家人在港澳旅游,某日两家人从香港口岸前往澳门口岸,当小辉一家乘坐穿梭巴士出发4分钟后,小亮一家乘坐跨境出租车出发,两车在全程中均保持匀速行驶,跨境出租车比穿梭巴士早到6.5分钟,过海关时间不考虑在内,两车距西人工岛的路程之和y(千米)与小辉家出发的时间x(分钟)之间的关系如图所示,穿梭巴士出发 分钟到达澳门口岸.
15.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为 .
三.解答题(共5小题)
16.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
17.实验室里,水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2cm,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两个容器的底面积之比为 ;
(2)图②中a的值为 ,b的值为 ;
(3)注水多少分钟后,乙与甲的水位相差1cm?
18.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A 200
B x 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
19.对于给定的△ABC,我们给出如下定义:
若点M是边BC上的一个定点,且以M为圆心的半圆上的所有点都在△ABC的内部或边上,则称这样的半圆为BC边上的点M关于△ABC的内半圆,并将半径最大的内半圆称为点M关于△ABC的最大内半圆.
若点M是边BC上的一个动点(M不与B,C重合),则在所有的点M关于△ABC的最大内半圆中,将半径最大的内半圆称为BC关于△ABC的内半圆.
(1)在Rt△ABC中,∠BAC=90°,AB=AC=2,
①如图1,点D在边BC上,且CD=1,直接写出点D关于△ABC的最大内半圆的半径长 ;
②如图2,画出BC关于△ABC的内半圆,并直接写出它的半径长 ;
(2)在平面直角坐标系xOy中,点E的坐标为(3,0),点P在直线y=x上运动(P不与O重合),将OE关于△OEP的内半圆半径记为R,当≤R≤1时,求点P的横坐标t的取值范围.
20.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(I)OE= ,OF= (用含t的代数式表示)
(II)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.
试题解析
一.选择题(共10小题)
1.某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q(升)与流出时间t(分钟)的函数关系式为( )
A.20﹣0.2t B.Q=20﹣0.2t(t≥0)
C.Q=20﹣0.2t D.Q=20﹣0.2t(0≤t≤100)
解:依题意有Q=20﹣0.2t,时间应≥0,流出的油不能多于20,
∴0.2t≤20,解得t≤100.
故选:D.
2.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
解:∵CD∥x轴,
∴从第50天开始植物的高度不变,
故①的说法正确;
设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴,
解得,
所以,直线AC的解析式为y=x+6(0≤x≤50),
故②的结论正确;
当x=40时,y=×40+6=14,
即第40天,该植物的高度为14厘米;
故③的说法正确;
当x=50时,y=×50+6=16,
即第50天,该植物的高度为16厘米;
故④的说法错误.
综上所述,正确的是①②③.
故选:A.
3.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
解:由函数图象,得:甲的速度为12÷3=4米/秒,乙的速度为400÷80=5米/秒,故A错误;
设乙离开起点x秒后,甲、乙两人第一次相遇,根据题意得:
5x=12+4x,
解得:x=12,
∴离开起点后,甲、乙两人第一次相遇时,距离起点为:12×5=60(米),
故B错误;
甲从起点到终点共用时为:400÷4=100(秒),
故C错误;
∵乙到达终点时,所用时间为80秒,甲先出发3秒,
∴此时甲行走的时间为83秒,
∴甲走的路程为:83×4=332(米),
∴乙到达终点时,甲、乙两人相距:400﹣332=68(米),故D正确;
故选:D.
4.一条公路沿线有A,B,C三个站点,甲、乙两车分别从A,B站点同时出发,匀速驶达C站.设甲、乙两车行驶xh后,与B站的距离分别为y1km,y2km.y1,y2与x的函数关系如图,则两车相遇的时间是( )
A.20min B.30min C.60min D.80min
解:由甲车行驶xh,与B站的距离分别为y1km的图象可知:
A,B两个站点的距离为:AB=20 km,甲车的速度为:20÷0.5=40km/h;
由乙车行驶xh,与B站的距离分别为y2km的图象可知:
B,C两个站点的距离为:BC=100 km,乙车的速度为:100÷4=25km/h;
两车相遇的时间就是甲车追上乙车所用时间:20÷(40﹣25)=h=80min
故选:D.
5.横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是公里/分;(2)乙在冲刺阶段的速度公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
A.1 B.2 C.3 D.4
解:甲前半程的速度是:5÷30=(公里/分),故(1)正确;
乙在冲刺阶段的速度为:(10﹣9)÷(75﹣70)=(公里/分),故(2)正确;
根据函数图象可知,在前半程甲的函数图象在乙的函数图象上方,所以在前半程甲一直领先于乙,故(3)正确;
当0≤x≤30时,,
当x>30时,y甲=,
当0≤x≤70时,y乙=x,
当70<x≤75时,y乙=x﹣3,
甲与乙刚好相距0.1公里时,即,
,解得:x=,
,解得:x=,
,解得:x=,
=10﹣0.1,解得:,
∴甲与乙刚好相距0.1公里的次数是4次,
故(4)正确;
故选:D.
6.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
解:
①小明骑车在平路上的速度为:4.5÷0.3=15(km/h),故①正确;
②小明骑车在上坡路的速度为:15﹣5=10(km/h),
小明骑车在下坡路的速度为:15+5=20(km/h).
∴小明在AB段上坡的时间为:(6.5﹣4.5)÷10=0.2(h),
BC段下坡的时间为:(6.5﹣4.5)÷20=0.1(h),
DE段平路的时间和OA段平路的时间相等为0.3h,
∴小明途中休息的时间为:1﹣0.3﹣0.2﹣0.1﹣0.3=0.1(h),故②正确;
③小明第一次经过距离甲地5.5km的地方时是上坡,其距离乙地还需骑车:(6.5﹣5.5)÷10=0.1h,
小明第二次经过距离甲地5.5km的地方时是下坡:(6.5﹣5.5)÷20=0.05h,
则两次的时间间隔是:0.1+0.05=0.15h,故③正确;
综上所述:①②③都正确;
故选:D.
7.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
解:A、由函数图象可知,甲走完全程需要82.3秒,乙走完全程需要90.2秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了300米,路程相同,本选项错误;
C、由函数图象可知,在47.8秒时,两队所走路程相等,均为174米,本选项正确;
D、由函数图象可知,从出发到13.7秒的时间段内,甲队的速度慢,本选项错误;
故选:C.
8.如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的路程大于小林游泳的路程;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中所有正确结论的序号是( )
A.①② B.①③ C.②④ D.③④
解:①错误.小明游泳的平均速度大于小林游泳的平均速度;
②正确.小明游泳的距离大于小林游泳的距离;
③错误,小明游75米时小林游了50米;
④正确.小明与小林共相遇5次;
故选:C.
9.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=3;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
解:∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确;
把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得
,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确;
把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③正确;
点A关于y轴对称的点为A'(2,0),
设过点C,A'的直线为y=ax+n,则
,解得,
∴y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确.
故选:D.
10.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选:B.
二.填空题(共5小题)
11.若汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,则S与t的函数关系式为 S=840﹣70t .
解:∵汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,
∴S与t的函数关系式为:S=840﹣70t.
故答案为:S=840﹣70t.
12.两港相距640千米,轮船以15千米/时的速度航行,t小时后剩下的距离y与t的函数关系式为 y=640﹣15t .
解;t小时行驶的距离=15t,
故可得y=640﹣15t.
故答案为:y=640﹣15t.
13.“渝黔高速铁路”即将在2017年底通车,通车后,重庆到贵阳、广州等地的时间将大大缩短.9月初,铁路局组织甲、乙两种列车在该铁路上进行试验运行,现两种列车同时从重庆出发,以各自速度匀速向A地行驶,乙列车到达A地后停止,甲列车到达A地停留20分钟后,再按原路以另一速度匀速返回重庆,已知两种列车分别距A地的路程y(km)与时间x(h)之间的函数图象如图所示.当乙列车到达A地时,则甲列车距离重庆 300 km.
解:设乙列车的速度为xkm/h,甲列车以ykm/h的速度向A地行驶,到达A地停留20分钟后,以zkm/h的速度返回重庆,则
根据3小时后,乙列车距离A地的路程为240,而甲列车到达A地,可得3x+240=3y,①
根据甲列车到达A地停留20分钟后,再返回重庆并与乙列车相遇的时刻为4小时,可得x+(1﹣)z=240,②
根据甲列车往返两地的路程相等,可得(﹣3﹣)z=3y,③
由①②③,可得x=120,y=200,z=180,
∴重庆到A地的路程为3×200=600(km),
∴乙列车到达A地的时间为600÷120=5(h),
∴当乙列车到达A地时,甲列车距离重庆的路程为600﹣(5﹣3﹣)×180=300(km),
故答案为:300.
14.2018年10月24日,世界上最长的港珠澳大桥正式通车,香港口岸途径西人工岛到达澳门口岸.五一期间小辉与小亮两家人在港澳旅游,某日两家人从香港口岸前往澳门口岸,当小辉一家乘坐穿梭巴士出发4分钟后,小亮一家乘坐跨境出租车出发,两车在全程中均保持匀速行驶,跨境出租车比穿梭巴士早到6.5分钟,过海关时间不考虑在内,两车距西人工岛的路程之和y(千米)与小辉家出发的时间x(分钟)之间的关系如图所示,穿梭巴士出发 42 分钟到达澳门口岸.
解:如图1,
由题意得:2AC=32,
AC=16,
设穿梭巴士的速度为m千米/分,跨境出租车的速度为n千米/分,
当y=0时,两家同时到达西人工岛,则,解得:,
设BC=s千米,则s+s﹣6.5m=45.5,
s=,
∴,即=,
解得:,
∴=,
m2﹣m=0,
m(m﹣1)=0,
m1=0(舍),m2=1,
∴s==26,
∴穿梭巴士的时间=+=42,
答:穿梭巴士出发42分钟到达澳门口岸.
故答案为:42.
15.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为 (﹣8,0)(3,0)(2,0)(,0) .
解:当x=0时,y=4,
当y=0时,x=﹣3,
即A(﹣3,0),B(0,4),
OA=3,OB=4,
由勾股定理得:AB=5,
有三种情况:①以A为圆心,以AB为半径交x轴于两点,此时AC=AB=5,
C的坐标是(2,0)和(﹣8,0);
②以B为圆心,以AB为半径交x轴于一点(A除外),此时AB=BC,OA=OC=3,
C的坐标是(3,0);
③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),A(﹣3,0),B(0,4),
∵AC=BC,由勾股定理得:(a+3)2=a2+42,
解得:a=,
∴C的坐标是(,0),
故答案为:(﹣8,0)(3,0)(2,0)(,0).
三.解答题(共5小题)
16.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
解:(1)设种植A,B两种蔬菜,每亩各需分别投入x,y万元
根据题意得
解得
答:种植A,B两种蔬菜,每亩各需分别投入0.6,0.8万元
(2)由题意得
w=0.8m+1.2×=﹣0.1m+150(0≤m≤)
(3)由(2)
m≥2×
解得m≥100
∵w=﹣0.1m+150
k=﹣0.1<0
∴w随m的增大而减小
∴当m=100时,w最大=140
=50
∴当种A蔬菜100亩,B种蔬菜50亩时,获得最大利润为140万元.
17.实验室里,水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2cm,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两个容器的底面积之比为 3:1 ;
(2)图②中a的值为 4 ,b的值为 8 ;
(3)注水多少分钟后,乙与甲的水位相差1cm?
解:(1)观察图象可知:注水2分钟时,丙容器水的高度是6cm,乙容器水的高度是2cm,
∵每分钟同时向乙、丙中注入的水量相同,即水的体积相等,
∴2S乙底面=6S丙底面,
∴S乙底面:S丙底面=6:2=3:1,
∴乙、丙两容器的底面积之比为3:1.
故答案为3:1.
(2)∵乙、丙两容器的底面积之比为3:1,丙容器注入2分钟到达6cm,
∴乙容器的水位达到6cm所需时间为:2+2=4(min),
b=(10﹣2+10×3+10)÷6=8(min),
故答案为:4;8;
(3)①设t分钟后,甲容器水位为1cm,根据题意得,
,
解得,t=1;
②当2≤x≤4时,设乙容器水位高度h与时间t的函数关系式为h=kt+b(k≠0),
∵图象经过(2,2)、(4,6)两点,
∴,
解得,
∴h=2t﹣2(2≤x≤4).
当h=3时,则2t﹣2=3,解得t=2.5;
③设t分钟后,甲容器水位为5cm,根据题意得,
2+6(t﹣4)=5,
解得t=4.5.
答:注水1分钟或2.5分钟或4.5分钟后,乙与甲的水位相差1cm.
18.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
解:(1)填表如下:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
依题意得:20(240﹣x)+25(x﹣40)=15x+18(300﹣x)
解得:x=200
两个蔬菜基地调运蔬菜的运费相等时x的值为200.
(2)w与x之间的函数关系为:w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200
由题意得:
∴40≤x≤240
∵在w=2x+9200中,2>0
∴w随x的增大而增大
∴当x=40时,总运费最小
此时调运方案为:
(3)由题意得w=(2﹣m)x+9200
∴0<m<2,(2)中调运方案总费用最小;
m=2时,在40≤x≤240的前提下调运方案的总费用不变;
2<m<15时,x=240总费用最小,其调运方案如下:
19.对于给定的△ABC,我们给出如下定义:
若点M是边BC上的一个定点,且以M为圆心的半圆上的所有点都在△ABC的内部或边上,则称这样的半圆为BC边上的点M关于△ABC的内半圆,并将半径最大的内半圆称为点M关于△ABC的最大内半圆.
若点M是边BC上的一个动点(M不与B,C重合),则在所有的点M关于△ABC的最大内半圆中,将半径最大的内半圆称为BC关于△ABC的内半圆.
(1)在Rt△ABC中,∠BAC=90°,AB=AC=2,
①如图1,点D在边BC上,且CD=1,直接写出点D关于△ABC的最大内半圆的半径长 ;
②如图2,画出BC关于△ABC的内半圆,并直接写出它的半径长 1 ;
(2)在平面直角坐标系xOy中,点E的坐标为(3,0),点P在直线y=x上运动(P不与O重合),将OE关于△OEP的内半圆半径记为R,当≤R≤1时,求点P的横坐标t的取值范围.
解:(1)①如图1,过D作DE⊥AC于E,
∵Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠C=∠B=45°,
∵CD=1,
∴BD=2﹣1>CD,
∴D到AC的距离小于到AB的距离,
∵△DEC是等腰直角三角形,
∴DE=,
即点D关于△ABC的最大内半圆的半径长是;
②当D为BC的中点时,BC关于△ABC的内半圆为⊙D,如图2,
∴BD=BC=,
同理可得:BC关于△ABC的内半圆半径DE=1.
(2)过点E作EF⊥OE,与直线y=x交于点F,设点M是OE上的动点,
i)当点P在线段OF上运动时(P不与O重合),OE关于△OEP的内半圆是以M为圆心,分别与OP,PE相切的半圆,如图3,连接PM,
∵直线OF:y=x
∴∠FOE=30°
由(1)可知:当M为线段中点时,存在OE关于△OEP的内半圆,
∴当R=时,如图3,DM=,此时PM⊥x轴,P的横坐标t=OM=;
如图4,当P与F重合时,M在∠EFO的角平分线上,⊙M分别与OF,FE相切,
此时R=1,P的横坐标t=OE=3;
∴当≤R≤1时,t的取值范围是≤t≤3.
ii)当点P在OF的延长线上运动时,OE关于△OEP的内半圆是以M为圆心,经过点E且与OP相切的半圆,如图5.
∴当 R=1 时,t的取值范围是t≥3.
iii)当点P 在OF的反向延长上运动时(P不与O重合),OE关于△OEP的内半圆是以M为圆心,经过点O且与EP相切的半圆,如图6.
∵∠FOE=∠OPE+∠OEP=30°,
∴∠OEP<30°,
∴OM<1,
当R=时,如图6,过P作PA⊥x轴于A,N是切点,连接MN,MN⊥PE,此时OM=MN=,ME=3﹣=,
∴EN===,
Rt△OPA中,∠POA=30°,OA=﹣t,
∴PA=﹣t,
∵∠ENM=∠EAP=90°,∠MEN=∠AEP,
∴△EMN∽△EPA,
∴,即=
解得:t=﹣,
∴当≤R<1时,t的取值范围是t≤﹣.
综上,点P在直线y=x上运动时(P不与O重合),当≤R≤1时,t的取值范围是t≤﹣或t≥.
20.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(I)OE= 6﹣t ,OF= t+ (用含t的代数式表示)
(II)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.
解:(I)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相等的速度沿AO向终点O运动.
∴当点E的运动时间为t(秒)时,
AE=t,OF=+t,
则OE=OA﹣AE=6﹣t;
故答案为:6﹣t,+t;
(II)①当t=1时,OF=1+=,OE=6﹣1=5,则CF=OC﹣OF=3﹣=,
由折叠可知:△OEF≌△DEF,
∴OF=DF=,
由勾股定理,得:CD=1,
∴D(1,3);
∵E(5,0),
∴设直线DE的解析式为:y=mx+n(k≠0),
把D(1,3)和E(5,0)代入得:,解得:,
∴直线DE的解析式为:y=﹣x+;
②∵MN∥DE,
∴MN的解析式为:y=﹣x+b,
当y=3时,﹣x+b=3,x=(b﹣3)=b﹣4,
∴CM=b﹣4,
分三种情况:
i)当M在边CB上时,如图2,
∴BM=6﹣CM=6﹣(b﹣4)=10﹣b,
DM=CM﹣1=b﹣5,
∵0≤DM<5,即0≤b﹣5<5,
∴≤b<,
∴S===15﹣2b=﹣2b+15(≤b<);
ii)当M与点B重合时,b=,S=0;
iii)当M在DB的延长线上时,如图3,
∴BM=CM﹣6=b﹣10,
DM=CM﹣1=b﹣5,
∵DM>5,即b﹣5>5,
∴b>,
∴S===2b﹣15(b>);
综上,S=.
_21?????????è?????(www.21cnjy.com)_
19.3 课题学习 选择方案 高频易错题集
一.选择题(共10小题)
1.某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q(升)与流出时间t(分钟)的函数关系式为( )
A.20﹣0.2t B.Q=20﹣0.2t(t≥0)
C.Q=20﹣0.2t D.Q=20﹣0.2t(0≤t≤100)
2.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
3.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
4.一条公路沿线有A,B,C三个站点,甲、乙两车分别从A,B站点同时出发,匀速驶达C站.设甲、乙两车行驶xh后,与B站的距离分别为y1km,y2km.y1,y2与x的函数关系如图,则两车相遇的时间是( )
A.20min B.30min C.60min D.80min
5.横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是公里/分;(2)乙在冲刺阶段的速度公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
A.1 B.2 C.3 D.4
6.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
7.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
8.如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的路程大于小林游泳的路程;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中所有正确结论的序号是( )
A.①② B.①③ C.②④ D.③④
9.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=3;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
10.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
二.填空题(共5小题)
11.若汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,则S与t的函数关系式为 .
12.两港相距640千米,轮船以15千米/时的速度航行,t小时后剩下的距离y与t的函数关系式为 .
13.“渝黔高速铁路”即将在2017年底通车,通车后,重庆到贵阳、广州等地的时间将大大缩短.9月初,铁路局组织甲、乙两种列车在该铁路上进行试验运行,现两种列车同时从重庆出发,以各自速度匀速向A地行驶,乙列车到达A地后停止,甲列车到达A地停留20分钟后,再按原路以另一速度匀速返回重庆,已知两种列车分别距A地的路程y(km)与时间x(h)之间的函数图象如图所示.当乙列车到达A地时,则甲列车距离重庆 km.
14.2018年10月24日,世界上最长的港珠澳大桥正式通车,香港口岸途径西人工岛到达澳门口岸.五一期间小辉与小亮两家人在港澳旅游,某日两家人从香港口岸前往澳门口岸,当小辉一家乘坐穿梭巴士出发4分钟后,小亮一家乘坐跨境出租车出发,两车在全程中均保持匀速行驶,跨境出租车比穿梭巴士早到6.5分钟,过海关时间不考虑在内,两车距西人工岛的路程之和y(千米)与小辉家出发的时间x(分钟)之间的关系如图所示,穿梭巴士出发 分钟到达澳门口岸.
15.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为 .
三.解答题(共5小题)
16.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
17.实验室里,水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2cm,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两个容器的底面积之比为 ;
(2)图②中a的值为 ,b的值为 ;
(3)注水多少分钟后,乙与甲的水位相差1cm?
18.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A 200
B x 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
19.对于给定的△ABC,我们给出如下定义:
若点M是边BC上的一个定点,且以M为圆心的半圆上的所有点都在△ABC的内部或边上,则称这样的半圆为BC边上的点M关于△ABC的内半圆,并将半径最大的内半圆称为点M关于△ABC的最大内半圆.
若点M是边BC上的一个动点(M不与B,C重合),则在所有的点M关于△ABC的最大内半圆中,将半径最大的内半圆称为BC关于△ABC的内半圆.
(1)在Rt△ABC中,∠BAC=90°,AB=AC=2,
①如图1,点D在边BC上,且CD=1,直接写出点D关于△ABC的最大内半圆的半径长 ;
②如图2,画出BC关于△ABC的内半圆,并直接写出它的半径长 ;
(2)在平面直角坐标系xOy中,点E的坐标为(3,0),点P在直线y=x上运动(P不与O重合),将OE关于△OEP的内半圆半径记为R,当≤R≤1时,求点P的横坐标t的取值范围.
20.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(I)OE= ,OF= (用含t的代数式表示)
(II)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.
试题解析
一.选择题(共10小题)
1.某油箱中存油20升,油从管道中匀速流出,流速为0.2升/分钟,则油箱中剩油量Q(升)与流出时间t(分钟)的函数关系式为( )
A.20﹣0.2t B.Q=20﹣0.2t(t≥0)
C.Q=20﹣0.2t D.Q=20﹣0.2t(0≤t≤100)
解:依题意有Q=20﹣0.2t,时间应≥0,流出的油不能多于20,
∴0.2t≤20,解得t≤100.
故选:D.
2.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间x(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下列说法正确的是( )
①从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
解:∵CD∥x轴,
∴从第50天开始植物的高度不变,
故①的说法正确;
设直线AC的解析式为y=kx+b(k≠0),
∵经过点A(0,6),B(30,12),
∴,
解得,
所以,直线AC的解析式为y=x+6(0≤x≤50),
故②的结论正确;
当x=40时,y=×40+6=14,
即第40天,该植物的高度为14厘米;
故③的说法正确;
当x=50时,y=×50+6=16,
即第50天,该植物的高度为16厘米;
故④的说法错误.
综上所述,正确的是①②③.
故选:A.
3.甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的是( )
A.乙的速度是4米/秒
B.离开起点后,甲、乙两人第一次相遇时,距离起点12米
C.甲从起点到终点共用时83秒
D.乙到达终点时,甲、乙两人相距68米
解:由函数图象,得:甲的速度为12÷3=4米/秒,乙的速度为400÷80=5米/秒,故A错误;
设乙离开起点x秒后,甲、乙两人第一次相遇,根据题意得:
5x=12+4x,
解得:x=12,
∴离开起点后,甲、乙两人第一次相遇时,距离起点为:12×5=60(米),
故B错误;
甲从起点到终点共用时为:400÷4=100(秒),
故C错误;
∵乙到达终点时,所用时间为80秒,甲先出发3秒,
∴此时甲行走的时间为83秒,
∴甲走的路程为:83×4=332(米),
∴乙到达终点时,甲、乙两人相距:400﹣332=68(米),故D正确;
故选:D.
4.一条公路沿线有A,B,C三个站点,甲、乙两车分别从A,B站点同时出发,匀速驶达C站.设甲、乙两车行驶xh后,与B站的距离分别为y1km,y2km.y1,y2与x的函数关系如图,则两车相遇的时间是( )
A.20min B.30min C.60min D.80min
解:由甲车行驶xh,与B站的距离分别为y1km的图象可知:
A,B两个站点的距离为:AB=20 km,甲车的速度为:20÷0.5=40km/h;
由乙车行驶xh,与B站的距离分别为y2km的图象可知:
B,C两个站点的距离为:BC=100 km,乙车的速度为:100÷4=25km/h;
两车相遇的时间就是甲车追上乙车所用时间:20÷(40﹣25)=h=80min
故选:D.
5.横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是公里/分;(2)乙在冲刺阶段的速度公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
A.1 B.2 C.3 D.4
解:甲前半程的速度是:5÷30=(公里/分),故(1)正确;
乙在冲刺阶段的速度为:(10﹣9)÷(75﹣70)=(公里/分),故(2)正确;
根据函数图象可知,在前半程甲的函数图象在乙的函数图象上方,所以在前半程甲一直领先于乙,故(3)正确;
当0≤x≤30时,,
当x>30时,y甲=,
当0≤x≤70时,y乙=x,
当70<x≤75时,y乙=x﹣3,
甲与乙刚好相距0.1公里时,即,
,解得:x=,
,解得:x=,
,解得:x=,
=10﹣0.1,解得:,
∴甲与乙刚好相距0.1公里的次数是4次,
故(4)正确;
故选:D.
6.从甲地到乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即返回甲地,途中休息了一段时间,假设小明骑车在平路、上坡、下坡时分别保持匀速前进,已知小明骑车上坡的速度比在平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km.设小明出发xh后,到达离甲地ykm的地方,图中的折线OABCDE表示y与x之间的函数关系.
①小明骑车在平路上的速度为15km/h
②小明途中休息了0.1h;
③小明从甲地去乙地来回过程中,两次经过距离甲地5.5km的地方的时间间隔为0.15h
则以上说法中正确的个数为( )
A.0 B.1 C.2 D.3
解:
①小明骑车在平路上的速度为:4.5÷0.3=15(km/h),故①正确;
②小明骑车在上坡路的速度为:15﹣5=10(km/h),
小明骑车在下坡路的速度为:15+5=20(km/h).
∴小明在AB段上坡的时间为:(6.5﹣4.5)÷10=0.2(h),
BC段下坡的时间为:(6.5﹣4.5)÷20=0.1(h),
DE段平路的时间和OA段平路的时间相等为0.3h,
∴小明途中休息的时间为:1﹣0.3﹣0.2﹣0.1﹣0.3=0.1(h),故②正确;
③小明第一次经过距离甲地5.5km的地方时是上坡,其距离乙地还需骑车:(6.5﹣5.5)÷10=0.1h,
小明第二次经过距离甲地5.5km的地方时是下坡:(6.5﹣5.5)÷20=0.05h,
则两次的时间间隔是:0.1+0.05=0.15h,故③正确;
综上所述:①②③都正确;
故选:D.
7.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
解:A、由函数图象可知,甲走完全程需要82.3秒,乙走完全程需要90.2秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了300米,路程相同,本选项错误;
C、由函数图象可知,在47.8秒时,两队所走路程相等,均为174米,本选项正确;
D、由函数图象可知,从出发到13.7秒的时间段内,甲队的速度慢,本选项错误;
故选:C.
8.如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的路程大于小林游泳的路程;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中所有正确结论的序号是( )
A.①② B.①③ C.②④ D.③④
解:①错误.小明游泳的平均速度大于小林游泳的平均速度;
②正确.小明游泳的距离大于小林游泳的距离;
③错误,小明游75米时小林游了50米;
④正确.小明与小林共相遇5次;
故选:C.
9.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组的解为;②△BCD为直角三角形;③S△ABD=3;④当PA+PC的值最小时,点P的坐标为(0,1).其中正确的说法个数有( )
A.1个 B.2个 C.3个 D.4个
解:∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确;
把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得
,解得,
∴直线l1:y=2x+4,
又∵直线l2:y=﹣x+m,
∴直线l1与直线l2互相垂直,即∠BCD=90°,
∴△BCD为直角三角形,
故②正确;
把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③正确;
点A关于y轴对称的点为A'(2,0),
设过点C,A'的直线为y=ax+n,则
,解得,
∴y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确.
故选:D.
10.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选:B.
二.填空题(共5小题)
11.若汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,则S与t的函数关系式为 S=840﹣70t .
解:∵汽车以70千米/时的平均速度由A地驶往相距840千米的B地,t小时后,汽车距B地S千米,
∴S与t的函数关系式为:S=840﹣70t.
故答案为:S=840﹣70t.
12.两港相距640千米,轮船以15千米/时的速度航行,t小时后剩下的距离y与t的函数关系式为 y=640﹣15t .
解;t小时行驶的距离=15t,
故可得y=640﹣15t.
故答案为:y=640﹣15t.
13.“渝黔高速铁路”即将在2017年底通车,通车后,重庆到贵阳、广州等地的时间将大大缩短.9月初,铁路局组织甲、乙两种列车在该铁路上进行试验运行,现两种列车同时从重庆出发,以各自速度匀速向A地行驶,乙列车到达A地后停止,甲列车到达A地停留20分钟后,再按原路以另一速度匀速返回重庆,已知两种列车分别距A地的路程y(km)与时间x(h)之间的函数图象如图所示.当乙列车到达A地时,则甲列车距离重庆 300 km.
解:设乙列车的速度为xkm/h,甲列车以ykm/h的速度向A地行驶,到达A地停留20分钟后,以zkm/h的速度返回重庆,则
根据3小时后,乙列车距离A地的路程为240,而甲列车到达A地,可得3x+240=3y,①
根据甲列车到达A地停留20分钟后,再返回重庆并与乙列车相遇的时刻为4小时,可得x+(1﹣)z=240,②
根据甲列车往返两地的路程相等,可得(﹣3﹣)z=3y,③
由①②③,可得x=120,y=200,z=180,
∴重庆到A地的路程为3×200=600(km),
∴乙列车到达A地的时间为600÷120=5(h),
∴当乙列车到达A地时,甲列车距离重庆的路程为600﹣(5﹣3﹣)×180=300(km),
故答案为:300.
14.2018年10月24日,世界上最长的港珠澳大桥正式通车,香港口岸途径西人工岛到达澳门口岸.五一期间小辉与小亮两家人在港澳旅游,某日两家人从香港口岸前往澳门口岸,当小辉一家乘坐穿梭巴士出发4分钟后,小亮一家乘坐跨境出租车出发,两车在全程中均保持匀速行驶,跨境出租车比穿梭巴士早到6.5分钟,过海关时间不考虑在内,两车距西人工岛的路程之和y(千米)与小辉家出发的时间x(分钟)之间的关系如图所示,穿梭巴士出发 42 分钟到达澳门口岸.
解:如图1,
由题意得:2AC=32,
AC=16,
设穿梭巴士的速度为m千米/分,跨境出租车的速度为n千米/分,
当y=0时,两家同时到达西人工岛,则,解得:,
设BC=s千米,则s+s﹣6.5m=45.5,
s=,
∴,即=,
解得:,
∴=,
m2﹣m=0,
m(m﹣1)=0,
m1=0(舍),m2=1,
∴s==26,
∴穿梭巴士的时间=+=42,
答:穿梭巴士出发42分钟到达澳门口岸.
故答案为:42.
15.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为 (﹣8,0)(3,0)(2,0)(,0) .
解:当x=0时,y=4,
当y=0时,x=﹣3,
即A(﹣3,0),B(0,4),
OA=3,OB=4,
由勾股定理得:AB=5,
有三种情况:①以A为圆心,以AB为半径交x轴于两点,此时AC=AB=5,
C的坐标是(2,0)和(﹣8,0);
②以B为圆心,以AB为半径交x轴于一点(A除外),此时AB=BC,OA=OC=3,
C的坐标是(3,0);
③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),A(﹣3,0),B(0,4),
∵AC=BC,由勾股定理得:(a+3)2=a2+42,
解得:a=,
∴C的坐标是(,0),
故答案为:(﹣8,0)(3,0)(2,0)(,0).
三.解答题(共5小题)
16.为落实“精准扶贫”,某村在政府的扶持下建起了蔬菜大棚基地,准备种植A,B两种蔬菜,若种植20亩A种蔬菜和30亩B种蔬菜,共需投入36万元;若种植30亩A种蔬菜和20亩B种蔬菜,共需投入34万元.
(1)种植A,B两种蔬菜,每亩各需投入多少万元?
(2)经测算,种植A种蔬菜每亩可获利0.8万元,种植B种蔬菜每亩可获利1.2万元,村里把100万元扶贫款全部用来种植这两种蔬菜,总获利w万元.设种植A种蔬菜m亩,求w关于m的函数关系式;
(3)在(2)的条件下,若要求A种蔬菜的种植面积不能少于B种蔬菜种植面积的2倍,请你设计出总获利最大的种植方案,并求出最大总获利.
解:(1)设种植A,B两种蔬菜,每亩各需分别投入x,y万元
根据题意得
解得
答:种植A,B两种蔬菜,每亩各需分别投入0.6,0.8万元
(2)由题意得
w=0.8m+1.2×=﹣0.1m+150(0≤m≤)
(3)由(2)
m≥2×
解得m≥100
∵w=﹣0.1m+150
k=﹣0.1<0
∴w随m的增大而减小
∴当m=100时,w最大=140
=50
∴当种A蔬菜100亩,B种蔬菜50亩时,获得最大利润为140万元.
17.实验室里,水平桌面上有甲、乙、丙三个高都是10cm的圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计),、现在三个容器中,只有甲中有水,水位高2cm,如图①所示,若每分钟同时向乙、丙中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.
(1)乙、丙两个容器的底面积之比为 3:1 ;
(2)图②中a的值为 4 ,b的值为 8 ;
(3)注水多少分钟后,乙与甲的水位相差1cm?
解:(1)观察图象可知:注水2分钟时,丙容器水的高度是6cm,乙容器水的高度是2cm,
∵每分钟同时向乙、丙中注入的水量相同,即水的体积相等,
∴2S乙底面=6S丙底面,
∴S乙底面:S丙底面=6:2=3:1,
∴乙、丙两容器的底面积之比为3:1.
故答案为3:1.
(2)∵乙、丙两容器的底面积之比为3:1,丙容器注入2分钟到达6cm,
∴乙容器的水位达到6cm所需时间为:2+2=4(min),
b=(10﹣2+10×3+10)÷6=8(min),
故答案为:4;8;
(3)①设t分钟后,甲容器水位为1cm,根据题意得,
,
解得,t=1;
②当2≤x≤4时,设乙容器水位高度h与时间t的函数关系式为h=kt+b(k≠0),
∵图象经过(2,2)、(4,6)两点,
∴,
解得,
∴h=2t﹣2(2≤x≤4).
当h=3时,则2t﹣2=3,解得t=2.5;
③设t分钟后,甲容器水位为5cm,根据题意得,
2+6(t﹣4)=5,
解得t=4.5.
答:注水1分钟或2.5分钟或4.5分钟后,乙与甲的水位相差1cm.
18.某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
解:(1)填表如下:
C D 总计/t
A (240﹣x) (x﹣40) 200
B x (300﹣x) 300
总计/t 240 260 500
依题意得:20(240﹣x)+25(x﹣40)=15x+18(300﹣x)
解得:x=200
两个蔬菜基地调运蔬菜的运费相等时x的值为200.
(2)w与x之间的函数关系为:w=20(240﹣x)+25(x﹣40)+15x+18(300﹣x)=2x+9200
由题意得:
∴40≤x≤240
∵在w=2x+9200中,2>0
∴w随x的增大而增大
∴当x=40时,总运费最小
此时调运方案为:
(3)由题意得w=(2﹣m)x+9200
∴0<m<2,(2)中调运方案总费用最小;
m=2时,在40≤x≤240的前提下调运方案的总费用不变;
2<m<15时,x=240总费用最小,其调运方案如下:
19.对于给定的△ABC,我们给出如下定义:
若点M是边BC上的一个定点,且以M为圆心的半圆上的所有点都在△ABC的内部或边上,则称这样的半圆为BC边上的点M关于△ABC的内半圆,并将半径最大的内半圆称为点M关于△ABC的最大内半圆.
若点M是边BC上的一个动点(M不与B,C重合),则在所有的点M关于△ABC的最大内半圆中,将半径最大的内半圆称为BC关于△ABC的内半圆.
(1)在Rt△ABC中,∠BAC=90°,AB=AC=2,
①如图1,点D在边BC上,且CD=1,直接写出点D关于△ABC的最大内半圆的半径长 ;
②如图2,画出BC关于△ABC的内半圆,并直接写出它的半径长 1 ;
(2)在平面直角坐标系xOy中,点E的坐标为(3,0),点P在直线y=x上运动(P不与O重合),将OE关于△OEP的内半圆半径记为R,当≤R≤1时,求点P的横坐标t的取值范围.
解:(1)①如图1,过D作DE⊥AC于E,
∵Rt△ABC中,∠BAC=90°,AB=AC=2,
∴∠C=∠B=45°,
∵CD=1,
∴BD=2﹣1>CD,
∴D到AC的距离小于到AB的距离,
∵△DEC是等腰直角三角形,
∴DE=,
即点D关于△ABC的最大内半圆的半径长是;
②当D为BC的中点时,BC关于△ABC的内半圆为⊙D,如图2,
∴BD=BC=,
同理可得:BC关于△ABC的内半圆半径DE=1.
(2)过点E作EF⊥OE,与直线y=x交于点F,设点M是OE上的动点,
i)当点P在线段OF上运动时(P不与O重合),OE关于△OEP的内半圆是以M为圆心,分别与OP,PE相切的半圆,如图3,连接PM,
∵直线OF:y=x
∴∠FOE=30°
由(1)可知:当M为线段中点时,存在OE关于△OEP的内半圆,
∴当R=时,如图3,DM=,此时PM⊥x轴,P的横坐标t=OM=;
如图4,当P与F重合时,M在∠EFO的角平分线上,⊙M分别与OF,FE相切,
此时R=1,P的横坐标t=OE=3;
∴当≤R≤1时,t的取值范围是≤t≤3.
ii)当点P在OF的延长线上运动时,OE关于△OEP的内半圆是以M为圆心,经过点E且与OP相切的半圆,如图5.
∴当 R=1 时,t的取值范围是t≥3.
iii)当点P 在OF的反向延长上运动时(P不与O重合),OE关于△OEP的内半圆是以M为圆心,经过点O且与EP相切的半圆,如图6.
∵∠FOE=∠OPE+∠OEP=30°,
∴∠OEP<30°,
∴OM<1,
当R=时,如图6,过P作PA⊥x轴于A,N是切点,连接MN,MN⊥PE,此时OM=MN=,ME=3﹣=,
∴EN===,
Rt△OPA中,∠POA=30°,OA=﹣t,
∴PA=﹣t,
∵∠ENM=∠EAP=90°,∠MEN=∠AEP,
∴△EMN∽△EPA,
∴,即=
解得:t=﹣,
∴当≤R<1时,t的取值范围是t≤﹣.
综上,点P在直线y=x上运动时(P不与O重合),当≤R≤1时,t的取值范围是t≤﹣或t≥.
20.如图,将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3),动点F从点O出发以每秒1个单位长度的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相同的速度沿AO向终点O运动,当点E、F其中一点到达终点时,另一点也停止运动设点E的运动时间为t:(秒)
(I)OE= 6﹣t ,OF= t+ (用含t的代数式表示)
(II)当t=1时,将△OEF沿EF翻折,点O恰好落在CB边上的点D处
①求点D的坐标及直线DE的解析式;
②点M是射线DB上的任意一点,过点M作直线DE的平行线,与x轴交于N点,设直线MN的解析式为y=kx+b,当点M与点B不重合时,S为△MBN的面积,当点M与点B重合时,S=0.求S与b之间的函数关系式,并求出自变量b的取值范围.
解:(I)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动秒时,动点E从点A出发以相等的速度沿AO向终点O运动.
∴当点E的运动时间为t(秒)时,
AE=t,OF=+t,
则OE=OA﹣AE=6﹣t;
故答案为:6﹣t,+t;
(II)①当t=1时,OF=1+=,OE=6﹣1=5,则CF=OC﹣OF=3﹣=,
由折叠可知:△OEF≌△DEF,
∴OF=DF=,
由勾股定理,得:CD=1,
∴D(1,3);
∵E(5,0),
∴设直线DE的解析式为:y=mx+n(k≠0),
把D(1,3)和E(5,0)代入得:,解得:,
∴直线DE的解析式为:y=﹣x+;
②∵MN∥DE,
∴MN的解析式为:y=﹣x+b,
当y=3时,﹣x+b=3,x=(b﹣3)=b﹣4,
∴CM=b﹣4,
分三种情况:
i)当M在边CB上时,如图2,
∴BM=6﹣CM=6﹣(b﹣4)=10﹣b,
DM=CM﹣1=b﹣5,
∵0≤DM<5,即0≤b﹣5<5,
∴≤b<,
∴S===15﹣2b=﹣2b+15(≤b<);
ii)当M与点B重合时,b=,S=0;
iii)当M在DB的延长线上时,如图3,
∴BM=CM﹣6=b﹣10,
DM=CM﹣1=b﹣5,
∵DM>5,即b﹣5>5,
∴b>,
∴S===2b﹣15(b>);
综上,S=.
_21?????????è?????(www.21cnjy.com)_
