高中物理选修3-5人教版17.4概率波(共23张ppt)
文档属性
| 名称 | 高中物理选修3-5人教版17.4概率波(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
第
4
节:概
率
波
经典的粒子经典的波(经典物理学关于粒子和波的概念)
经典的粒子:
具有空间大小、质量、电量等,遵从牛顿第二定律,任意
时刻有确定的位置和速度,以及确定的运动轨迹。
经典的波:
某种物理量呈时空周期性的分布
(
确定的点处具时间周期
性,确定的方向上具有空间周期性),特征是具有频率和波长。
显然,在经典的传统观念中,一个客体要么是粒子,要么是波,非此即彼!
为什么光子、电子和质子等微观粒子又能集这两种互不相容的属性于一身呢?
一、概率波
明纹处到达的光子数多,暗纹到达的光子少
这是否可以认为,是光子之间的相互作用使它表现出了波动行,而不是光子本身就具有波动性呢?
一个光子通过狭缝后到底落在屏上的哪一点呢?
1926年德国物理学家波恩指出:光子落在明处的概率大,落在暗处的概率小。
光子在空间出现的概率可以通过波动的规律确定,所以从光子的概念上看,光波是刻画光子在空间的概率分布的一种概率波。
电子双缝衍射
1.
用足够强的电子束进行双缝衍射
——
出现了明暗相间的衍射条纹,体现电子的波动性
——
衍射条纹掩饰了电子的粒子性
未能体现电子在空间分布的概率性质
——
得到的结果与光的双缝衍射结果一样
2.
用非常弱的电子束进行双缝衍射
单个电子的运动方向是完全不确定的
—
具有概率分布
一定条件下,电子运动方向的概率具有确定的规律
开始电子打在屏幕上的位置是任意的
随着时间推移,电子具有稳定的分布
出现清晰衍射条纹
—
和强电子束在短时间形成的一样
——
经典的波是介质中质元共同振动形成的
双缝衍射中体现为无论电子强度多么弱,屏幕上
出现的是强弱连续分布的衍射条纹
——
实际上在电子强度弱的情形中,电子在屏幕上
的分布是随机的,完全不确定的
物质波不是经典波
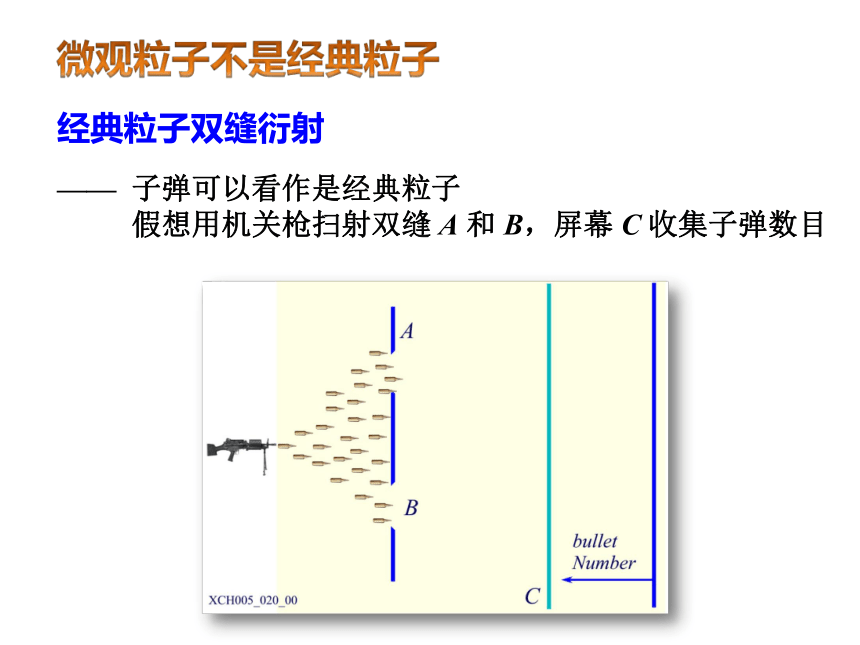
经典粒子双缝衍射
——
子弹可以看作是经典粒子
假想用机关枪扫射双缝
A
和
B,屏幕
C
收集子弹数目
微观粒子不是经典粒子
1.
将狭缝
B
挡住
——
子弹通过
A
在屏幕
C
上有一定的分布
——
类似于单缝衍射的中央主极大
P1
—
子弹落在中央主极大范围的概率分布
2.
将狭缝
A
挡住
——
子弹通过狭缝
B
在屏幕
C
上有一定的分布
——
类似于单缝衍射的中央主极大
P2
—
子弹落在中央主极大范围的概率分布
3.
A
和
B
狭缝同时打开
——
子弹是经典粒子
原来通过
A
狭缝的子弹
——
还是通过
A
原来通过
B
狭缝的子弹
——
还是通过
B
屏幕
C
上子弹的概率分布:
不因两个狭缝同时打开每颗子弹会有新的选择!
——
电子双缝衍射
——
电子枪发射出的电子,在屏幕
P
上观察电子数目
1.
将狭缝
B
挡住
——
电子通过狭缝
A
在屏幕
C
有一定分布
——
类似于单缝衍射的中
央主极大
2.
将狭缝
A
挡住
——
电子通过狭缝
B
在屏幕
C
上有一定的分布
类似于单缝衍射的中央主极大
3.
A
和
B
狭缝同时打开
——
如果电子是经典粒子
原来通过
A
狭缝的电子
——
还是通过
A
原来通过
B
狭缝的电子
——
还是通过
B
屏幕上电子的概率分布:
屏幕
C
——
实际观察到类似光的双缝衍射条纹
屏幕
C
上电子的概率分布
——
只开一个狭缝和同时开两个狭缝
电子运动的方向具有随机性
A
和
B
狭缝同时开时电子似乎“知道”
两个狭缝都打开!
双缝和屏幕之间到底发生了什么?
屏幕上电子的分布
——
有了新的概率分布
电子不是经典粒子
光子在某处出现的概率由光在该处的强度决定
I
大,光子出现概率大
I
小,光子出现概率小
统一于概率波理论
单缝衍射
光子在某处出现的概率和该处光振幅的平方成正比
二、电子干涉条纹对概率波的验证
与电子等微观粒子相联系的物质波也是刻画粒子在空间分布的概率波
单个粒子
位置不确定
大量粒子
确定的宏观结果
如干涉条纹
1.
概率波
光子在空间出现的概率可以通过波动的规律确定,光波是刻画光子在空间的概率分布的一种概率波。
2.
电子干涉条纹对概率波的验证
单个粒子
位置不确定
大量粒子
确定的宏观结果
如干涉条纹
B
1.
光电效应的四条规律中,波动说仅能解释的一条规
律是
(
)
A.
入射光的频率必须大于或等于被照金属的极限频率
才能产生光电效应
B.
发生光电效应时,光电流的强度与入射光的强度成
正比
C.
光电子的最大初动能随入射光频率的增大而增大
D.
光电效应发生的时间极短,一般不超过
10??
s
C
2.
下列关于光的波粒二象性的说法中,正确的是
(
)
A.
有的光是波,有的光是粒子
B.
光子与电子是同样的一种粒子
C.
光的波长越长,其波动性越显著;波长越短,其粒子
性越显著
D.
大量光子产生的效果往往显示粒子性
3.下列说法不正确的是
(
)
A.
光是一种电磁波
B.
光是一种概率波
C.
光子相当于高速运动的质点
D.
光的直线传播只是宏观近似规律
C
第
4
节:概
率
波
经典的粒子经典的波(经典物理学关于粒子和波的概念)
经典的粒子:
具有空间大小、质量、电量等,遵从牛顿第二定律,任意
时刻有确定的位置和速度,以及确定的运动轨迹。
经典的波:
某种物理量呈时空周期性的分布
(
确定的点处具时间周期
性,确定的方向上具有空间周期性),特征是具有频率和波长。
显然,在经典的传统观念中,一个客体要么是粒子,要么是波,非此即彼!
为什么光子、电子和质子等微观粒子又能集这两种互不相容的属性于一身呢?
一、概率波
明纹处到达的光子数多,暗纹到达的光子少
这是否可以认为,是光子之间的相互作用使它表现出了波动行,而不是光子本身就具有波动性呢?
一个光子通过狭缝后到底落在屏上的哪一点呢?
1926年德国物理学家波恩指出:光子落在明处的概率大,落在暗处的概率小。
光子在空间出现的概率可以通过波动的规律确定,所以从光子的概念上看,光波是刻画光子在空间的概率分布的一种概率波。
电子双缝衍射
1.
用足够强的电子束进行双缝衍射
——
出现了明暗相间的衍射条纹,体现电子的波动性
——
衍射条纹掩饰了电子的粒子性
未能体现电子在空间分布的概率性质
——
得到的结果与光的双缝衍射结果一样
2.
用非常弱的电子束进行双缝衍射
单个电子的运动方向是完全不确定的
—
具有概率分布
一定条件下,电子运动方向的概率具有确定的规律
开始电子打在屏幕上的位置是任意的
随着时间推移,电子具有稳定的分布
出现清晰衍射条纹
—
和强电子束在短时间形成的一样
——
经典的波是介质中质元共同振动形成的
双缝衍射中体现为无论电子强度多么弱,屏幕上
出现的是强弱连续分布的衍射条纹
——
实际上在电子强度弱的情形中,电子在屏幕上
的分布是随机的,完全不确定的
物质波不是经典波
经典粒子双缝衍射
——
子弹可以看作是经典粒子
假想用机关枪扫射双缝
A
和
B,屏幕
C
收集子弹数目
微观粒子不是经典粒子
1.
将狭缝
B
挡住
——
子弹通过
A
在屏幕
C
上有一定的分布
——
类似于单缝衍射的中央主极大
P1
—
子弹落在中央主极大范围的概率分布
2.
将狭缝
A
挡住
——
子弹通过狭缝
B
在屏幕
C
上有一定的分布
——
类似于单缝衍射的中央主极大
P2
—
子弹落在中央主极大范围的概率分布
3.
A
和
B
狭缝同时打开
——
子弹是经典粒子
原来通过
A
狭缝的子弹
——
还是通过
A
原来通过
B
狭缝的子弹
——
还是通过
B
屏幕
C
上子弹的概率分布:
不因两个狭缝同时打开每颗子弹会有新的选择!
——
电子双缝衍射
——
电子枪发射出的电子,在屏幕
P
上观察电子数目
1.
将狭缝
B
挡住
——
电子通过狭缝
A
在屏幕
C
有一定分布
——
类似于单缝衍射的中
央主极大
2.
将狭缝
A
挡住
——
电子通过狭缝
B
在屏幕
C
上有一定的分布
类似于单缝衍射的中央主极大
3.
A
和
B
狭缝同时打开
——
如果电子是经典粒子
原来通过
A
狭缝的电子
——
还是通过
A
原来通过
B
狭缝的电子
——
还是通过
B
屏幕上电子的概率分布:
屏幕
C
——
实际观察到类似光的双缝衍射条纹
屏幕
C
上电子的概率分布
——
只开一个狭缝和同时开两个狭缝
电子运动的方向具有随机性
A
和
B
狭缝同时开时电子似乎“知道”
两个狭缝都打开!
双缝和屏幕之间到底发生了什么?
屏幕上电子的分布
——
有了新的概率分布
电子不是经典粒子
光子在某处出现的概率由光在该处的强度决定
I
大,光子出现概率大
I
小,光子出现概率小
统一于概率波理论
单缝衍射
光子在某处出现的概率和该处光振幅的平方成正比
二、电子干涉条纹对概率波的验证
与电子等微观粒子相联系的物质波也是刻画粒子在空间分布的概率波
单个粒子
位置不确定
大量粒子
确定的宏观结果
如干涉条纹
1.
概率波
光子在空间出现的概率可以通过波动的规律确定,光波是刻画光子在空间的概率分布的一种概率波。
2.
电子干涉条纹对概率波的验证
单个粒子
位置不确定
大量粒子
确定的宏观结果
如干涉条纹
B
1.
光电效应的四条规律中,波动说仅能解释的一条规
律是
(
)
A.
入射光的频率必须大于或等于被照金属的极限频率
才能产生光电效应
B.
发生光电效应时,光电流的强度与入射光的强度成
正比
C.
光电子的最大初动能随入射光频率的增大而增大
D.
光电效应发生的时间极短,一般不超过
10??
s
C
2.
下列关于光的波粒二象性的说法中,正确的是
(
)
A.
有的光是波,有的光是粒子
B.
光子与电子是同样的一种粒子
C.
光的波长越长,其波动性越显著;波长越短,其粒子
性越显著
D.
大量光子产生的效果往往显示粒子性
3.下列说法不正确的是
(
)
A.
光是一种电磁波
B.
光是一种概率波
C.
光子相当于高速运动的质点
D.
光的直线传播只是宏观近似规律
C
