【高频易错题汇编】9.2 一元一次不等式 (含解析)
文档属性
| 名称 | 【高频易错题汇编】9.2 一元一次不等式 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 308.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 13:17:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
9.2 一元一次不等式 高频易错题集
一.选择题(共10小题)
1.不等式x+1<﹣1的解集是( )
A.x<0 B.x<﹣2 C.x>0 D.x<2
2.已知a、b为常数,若ax+b>0的解集是,则bx﹣a<0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
3.满足不等式的x的取值范围是( )
A.x>3 B.x< C.x>3或x< D.无法确定
4.不等式4(x﹣2)>2(3x﹣7)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
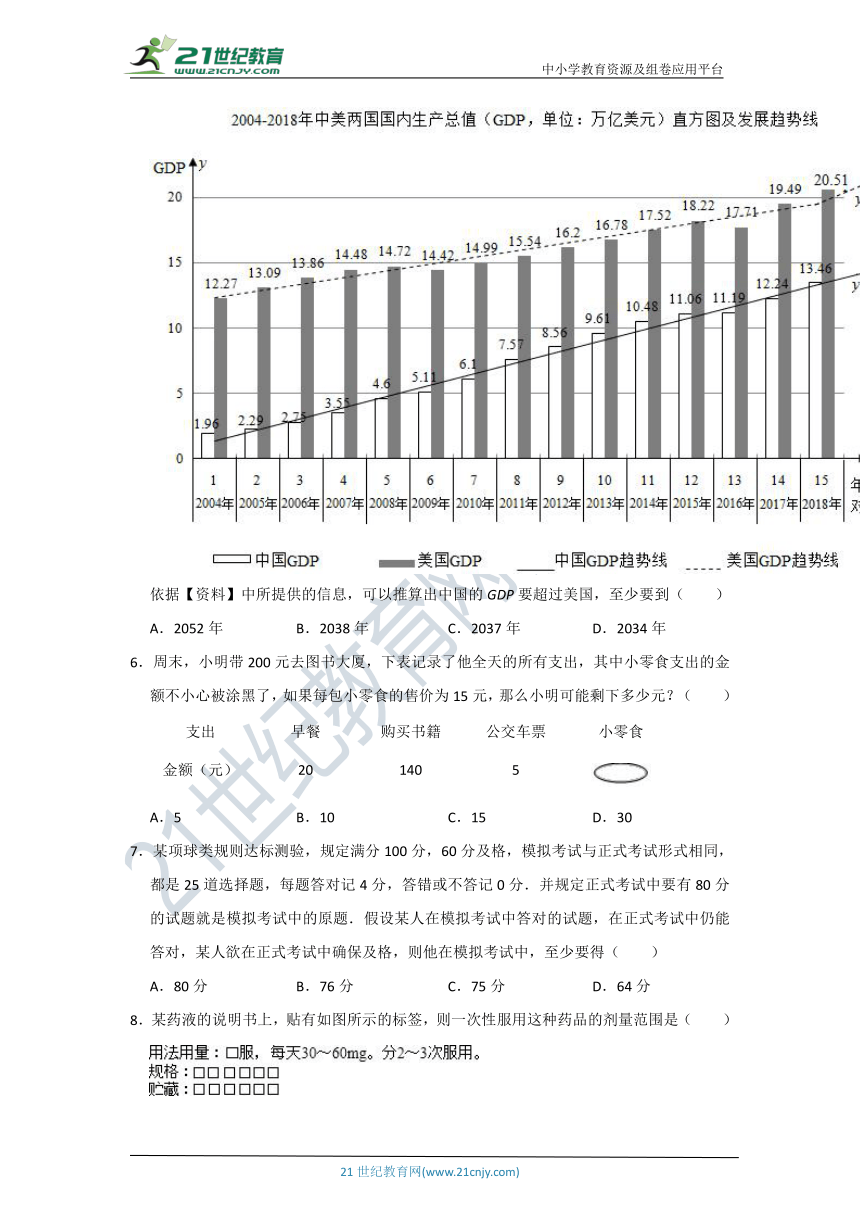
5.阅读【资料】,完成第8、9题.
【资料】:如图,这是根据_??????è???????????_绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)21世纪教育网版权所有
2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线
依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到( )
A.2052年 B.2038年 C.2037年 D.2034年
6.周末,小明带200元_??????????¤§??????_下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下多少元?( )
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
A.5 B.10 C.15 D.30
7.某项球类规则达标测_é?????è§??????????_100分,60分及格,模拟考试与正式考试形式相同,都是25道选择题,每题答对记4分,答错或不答记0分.并规定正式考试中要有80分的试题就是模拟考试中的原题.假设某人在模拟考试中答对的试题,在正式考试中仍能答对,某人欲在正式考试中确保及格,则他在模拟考试中,至少要得( )
A.80分 B.76分 C.75分 D.64分
8.某药液的说明书上,贴有如图所示的标签,则一次性服用这种药品的剂量范围是( )
A.10mg~20mg B.15mg~30mg C.15mg~20mg D.10mg~30mg
9.百货商场有一种商品的合格率为97%,已知该商品有400件,请问该商场至少还需准备( )件商品供消费者更换.21教育网
A.9个 B.15个 C.12个 D.13个
10.奥运会十米跳台跳水_???è?????è§???????_:每个跳水运动员有十次跳水机会,每次的最高得分是100分,按最终得分决定名次.某运动员前7次跳水共得580分,如果他要打破850分的奥运会纪录,第8次跳水至少要高于( )21cnjy.com
A.60分 B.70分 C.80分 D.100分
二.填空题(共5小题)
11.不等式x+2>3x﹣4的解集是 .
12.如果关于x的不等式(a﹣1)x>a+5和2x>4的解集相同,则a的值为 .
13.若不等式3x﹣m≤0的正整数解是1,2,3,则m的取值范围是 .
14.若关于x的不等式2x﹣3a+2≥0的最小整数解为5,则实数a的取值为
15.用不等式表示语句“a与b的差不大于﹣2”为 .
三.解答题(共5小题)
16.已知不等式x﹣2>x与ax﹣3>2x的解集相同,求a的值.
17.阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.21·cn·jy·com
求绝对值不等式|x|>3的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:www.21-cn-jy.com
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式|x|>3的解集为:x<﹣3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 ;
②|x|<2.5的解集是 .
(2)求绝对值不等式|x﹣3|+5>9的解集.
(3)直接写出不等式x2>4的解集是 .
18.如果不等式3x﹣m≤0的正整数解是1,2,3,那么m的范围是什么?
19.已知不等式3x﹣a≤0的正整数解恰是1,2,3,求a的取值范围.
20.某水果店以每千克_6????????·???è??_进一批水果,由于销售状况良好,该店又购进一些同一种水果,第二次进货价格比第一次每千克便宜了1元,已知两次一共进货600千克.
(1)若该水果店两次进货的总价格不超过3200元,求第一次至多购进水果多少千克?
(2)在(1_??????????????????_以第一次购进最大重量时的数量进货,在销售过程中,第一次购进的水果有3%的损耗,其售价比其进价多2a元,第二次购进的水果有5%的损耗,其售价比其进价多a元,该水果店希望售完两批水果后获利31.75%,求a的值.
9.2 一元一次不等式 高频易错题集
试题解析
一.选择题(共10小题)
1.不等式x+1<﹣1的解集是( )
A.x<0 B.x<﹣2 C.x>0 D.x<2
解:x+1<﹣1,
x<﹣2,
故选:B.
2.已知a、b为常数,若ax+b>0的解集是,则bx﹣a<0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
解:∵ax+b>0的解集是,
由于不等号的方向发生了变化,
∴a<0,又﹣=,即a=﹣3b,
∴b>0,
不等式bx﹣a<0即bx+3b<0,
解得x<﹣3.
故选:B.
3.满足不等式的x的取值范围是( )
A.x>3 B.x< C.x>3或x< D.无法确定
解:①当x≥0且x≠3时,,∴
若x>3,则(1)式成立;
若0≤x<3,则5<3﹣x,解得x<﹣2与0≤x<3矛盾.
故x>3;
②当x<0时,,解得x<(2);
由以上知x的取值范围是x>3或x<.
故选:C.
4.不等式4(x﹣2)>2(3x﹣7)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
解:去括号得:4x﹣8>6x﹣14,
移项得:﹣2x>﹣6,
解得:x<3,
则不等式的非负整数解为0,1,2,共3个.
故选:D.
5.阅读【资料】,完成第8、9题.
【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)
2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线
依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到( )
A.2052年 B.2038年 C.2037年 D.2034年
解:由图表中美GDP趋势线,要使得中国的GDP要超过美国,则有
0.86x+0.468>0.53x+11.778
解得x>
∵x为正整数
∴x≥35
∴中国的GDP要超过美国,至少要到2038年.
故选:B.
6.周末,小明带200元去图书大厦,下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下多少元?( )
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
A.5 B.10 C.15 D.30
解:设小明买了x包小零食,依题意得:
小明剩下的人民币可以表示:200﹣20﹣140﹣5﹣15x,
整理得:(35﹣15x)元﹣﹣﹣﹣﹣﹣①
0<20+140+5+15x<200,
解得:0<x<,
又∵x是取正整数,
∴x的取值为1或2,
(Ⅰ)当x=1时代入①得:35﹣15x=35﹣15×1=20元,
(Ⅱ)当x=2时代入①得:35﹣15x=35﹣15×2=5元.
从A、B、C、D四个选项中,符合题意只有A答案.
故选:A.
7.某项球类规则达标测验,规定满分100分,60分及格,模拟考试与正式考试形式相同,都是25道选择题,每题答对记4分,答错或不答记0分.并规定正式考试中要有80分的试题就是模拟考试中的原题.假设某人在模拟考试中答对的试题,在正式考试中仍能答对,某人欲在正式考试中确保及格,则他在模拟考试中,至少要得( )
A.80分 B.76分 C.75分 D.64分
解:设在模拟考试中至少要得x分
由题意列式
解得x≥80.即某人欲在正式考试中确保及格,则他在模拟考试中至少要得80分.
故选:A.
8.某药液的说明书上,贴有如图所示的标签,则一次性服用这种药品的剂量范围是( )
A.10mg~20mg B.15mg~30mg C.15mg~20mg D.10mg~30mg
解:依题意得:一次用药剂量的最大值===30mg
一次用药剂量的最小者===10mg
故:一次性服用这种药品的剂量范围是10mg~30mg
故选:D.
9.百货商场有一种商品的合格率为97%,已知该商品有400件,请问该商场至少还需准备( )件商品供消费者更换.
A.9个 B.15个 C.12个 D.13个
解:设至少还准备x件商品供消费者更换,
依题意可得(400+x)×97%≥400
解得:x≥12,又因为x取整数,则x最小是13.
故选:D.
10.奥运会十米跳台跳水比赛的规则是:每个跳水运动员有十次跳水机会,每次的最高得分是100分,按最终得分决定名次.某运动员前7次跳水共得580分,如果他要打破850分的奥运会纪录,第8次跳水至少要高于( )
A.60分 B.70分 C.80分 D.100分
解:设不能少于x分,
由题意得,580+x+100+100>850,
解得:x>70,
即第8次跳水不能少于70分.
故选:B.
二.填空题(共5小题)
11.不等式x+2>3x﹣4的解集是 x<3 .
解:移项,得x﹣3x>﹣4﹣2,
合并同类项,得﹣2x>﹣6,
化系数为1,得 x<3,
故答案为x<3.
12.如果关于x的不等式(a﹣1)x>a+5和2x>4的解集相同,则a的值为 7 .
解:由2x>4得x>2,
∵两个不等式的解集相同,
∴由(a﹣1)x>a+5可得x>,
∴=2,
解得a=7.
故答案为:7.
13.若不等式3x﹣m≤0的正整数解是1,2,3,则m的取值范围是 9≤m<12 .
解:不等式3x﹣m≤0的解集是x≤,
∵正整数解是1,2,3,
∴m的取值范围是3≤<4即9≤m<12.
故答案为:9≤m<12.
14.若关于x的不等式2x﹣3a+2≥0的最小整数解为5,则实数a的取值为 <a≤4
解:解不等式2x﹣3a+2≥0得x≥,
∵不等式的最小整数解为5,
∴4≤5,
∴<a≤4,
故答案为:<a≤4.
15.用不等式表示语句“a与b的差不大于﹣2”为 a﹣b≤﹣2 .
解:“a与b的差不大于﹣2”用不等式表示为:a﹣b≤﹣2.
故答案为:a﹣b≤﹣2.
三.解答题(共5小题)
16.已知不等式x﹣2>x与ax﹣3>2x的解集相同,求a的值.
解:解不等式x﹣2>x得,x<﹣;
由不等式ax﹣3>2x得,(a﹣2)x>3,
∵两不等式的解集相同,
∴a﹣2<0,
∴x<,
∴=﹣,解得a=.
17.阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式|x|>3的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式|x|>3的解集为:x<﹣3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 x<﹣1或x>1 ;
②|x|<2.5的解集是 ﹣2.5<x<2.5 .
(2)求绝对值不等式|x﹣3|+5>9的解集.
(3)直接写出不等式x2>4的解集是 x<﹣2或x>2. .
解:(1)根据阅读材料可知:
①|x|>1的解集是x<﹣1或x>1;
②|x|<2.5的解集是﹣2.5<x<2.5.
故答案为:x<﹣1或x>1;﹣2.5<x<2.5.
(2)|x﹣3|+5>9
|x﹣3|>4
∴x﹣3<﹣4或x﹣3>4
解得x<﹣1或x>7;
(3)x2>4
解得x<﹣2或x>2.
故答案为:x<﹣2或x>2.
18.如果不等式3x﹣m≤0的正整数解是1,2,3,那么m的范围是什么?
解:先求出不等式的解集为x≤,
又它的正整数解只有1,2,3,
如图:
说明3≤<4,
求得9≤m<12.
19.已知不等式3x﹣a≤0的正整数解恰是1,2,3,求a的取值范围.
解:3x﹣a≤0,
移项得,3x≤a,
系数化为1得,x≤.
∵不等式3x﹣a≤0的正整数解恰是1,2,3,
∴3≤x<4,
∴3≤<4时,即9≤a<12时,不等式3x﹣a≤0的正整数解恰是1,2,3.
故a的取值范围是9≤a<12.
20.某水果店以每千克6元的价格购进一批水果,由于销售状况良好,该店又购进一些同一种水果,第二次进货价格比第一次每千克便宜了1元,已知两次一共进货600千克.
(1)若该水果店两次进货的总价格不超过3200元,求第一次至多购进水果多少千克?
(2)在(1)的条件下,以第一次购进最大重量时的数量进货,在销售过程中,第一次购进的水果有3%的损耗,其售价比其进价多2a元,第二次购进的水果有5%的损耗,其售价比其进价多a元,该水果店希望售完两批水果后获利31.75%,求a的值.
解:(1)设第一次购进水果x千克,
根据题意,得:6x+5(600﹣x)≤3200,
解得:x≤200,
答:第一次至多购进水果200千克;
(2)第一次至多购进水果200千克,则第二次购进400千克,根据题意,得:
(6+2a)×200(1﹣3%)﹣200×6+(5+a)×400(1﹣5%)﹣400×5=3200×31.75%,
解得:a=1.5
故a的值为1.5.
_21?????????è?????(www.21cnjy.com)_
9.2 一元一次不等式 高频易错题集
一.选择题(共10小题)
1.不等式x+1<﹣1的解集是( )
A.x<0 B.x<﹣2 C.x>0 D.x<2
2.已知a、b为常数,若ax+b>0的解集是,则bx﹣a<0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
3.满足不等式的x的取值范围是( )
A.x>3 B.x< C.x>3或x< D.无法确定
4.不等式4(x﹣2)>2(3x﹣7)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
5.阅读【资料】,完成第8、9题.
【资料】:如图,这是根据_??????è???????????_绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)21世纪教育网版权所有
2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线
依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到( )
A.2052年 B.2038年 C.2037年 D.2034年
6.周末,小明带200元_??????????¤§??????_下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下多少元?( )
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
A.5 B.10 C.15 D.30
7.某项球类规则达标测_é?????è§??????????_100分,60分及格,模拟考试与正式考试形式相同,都是25道选择题,每题答对记4分,答错或不答记0分.并规定正式考试中要有80分的试题就是模拟考试中的原题.假设某人在模拟考试中答对的试题,在正式考试中仍能答对,某人欲在正式考试中确保及格,则他在模拟考试中,至少要得( )
A.80分 B.76分 C.75分 D.64分
8.某药液的说明书上,贴有如图所示的标签,则一次性服用这种药品的剂量范围是( )
A.10mg~20mg B.15mg~30mg C.15mg~20mg D.10mg~30mg
9.百货商场有一种商品的合格率为97%,已知该商品有400件,请问该商场至少还需准备( )件商品供消费者更换.21教育网
A.9个 B.15个 C.12个 D.13个
10.奥运会十米跳台跳水_???è?????è§???????_:每个跳水运动员有十次跳水机会,每次的最高得分是100分,按最终得分决定名次.某运动员前7次跳水共得580分,如果他要打破850分的奥运会纪录,第8次跳水至少要高于( )21cnjy.com
A.60分 B.70分 C.80分 D.100分
二.填空题(共5小题)
11.不等式x+2>3x﹣4的解集是 .
12.如果关于x的不等式(a﹣1)x>a+5和2x>4的解集相同,则a的值为 .
13.若不等式3x﹣m≤0的正整数解是1,2,3,则m的取值范围是 .
14.若关于x的不等式2x﹣3a+2≥0的最小整数解为5,则实数a的取值为
15.用不等式表示语句“a与b的差不大于﹣2”为 .
三.解答题(共5小题)
16.已知不等式x﹣2>x与ax﹣3>2x的解集相同,求a的值.
17.阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.21·cn·jy·com
求绝对值不等式|x|>3的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:www.21-cn-jy.com
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式|x|>3的解集为:x<﹣3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 ;
②|x|<2.5的解集是 .
(2)求绝对值不等式|x﹣3|+5>9的解集.
(3)直接写出不等式x2>4的解集是 .
18.如果不等式3x﹣m≤0的正整数解是1,2,3,那么m的范围是什么?
19.已知不等式3x﹣a≤0的正整数解恰是1,2,3,求a的取值范围.
20.某水果店以每千克_6????????·???è??_进一批水果,由于销售状况良好,该店又购进一些同一种水果,第二次进货价格比第一次每千克便宜了1元,已知两次一共进货600千克.
(1)若该水果店两次进货的总价格不超过3200元,求第一次至多购进水果多少千克?
(2)在(1_??????????????????_以第一次购进最大重量时的数量进货,在销售过程中,第一次购进的水果有3%的损耗,其售价比其进价多2a元,第二次购进的水果有5%的损耗,其售价比其进价多a元,该水果店希望售完两批水果后获利31.75%,求a的值.
9.2 一元一次不等式 高频易错题集
试题解析
一.选择题(共10小题)
1.不等式x+1<﹣1的解集是( )
A.x<0 B.x<﹣2 C.x>0 D.x<2
解:x+1<﹣1,
x<﹣2,
故选:B.
2.已知a、b为常数,若ax+b>0的解集是,则bx﹣a<0的解集是( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
解:∵ax+b>0的解集是,
由于不等号的方向发生了变化,
∴a<0,又﹣=,即a=﹣3b,
∴b>0,
不等式bx﹣a<0即bx+3b<0,
解得x<﹣3.
故选:B.
3.满足不等式的x的取值范围是( )
A.x>3 B.x< C.x>3或x< D.无法确定
解:①当x≥0且x≠3时,,∴
若x>3,则(1)式成立;
若0≤x<3,则5<3﹣x,解得x<﹣2与0≤x<3矛盾.
故x>3;
②当x<0时,,解得x<(2);
由以上知x的取值范围是x>3或x<.
故选:C.
4.不等式4(x﹣2)>2(3x﹣7)的非负整数解的个数为( )
A.0个 B.1个 C.2个 D.3个
解:去括号得:4x﹣8>6x﹣14,
移项得:﹣2x>﹣6,
解得:x<3,
则不等式的非负整数解为0,1,2,共3个.
故选:D.
5.阅读【资料】,完成第8、9题.
【资料】:如图,这是根据公开资料整理绘制而成的2004﹣2018年中美两国国内生产总值(GDP)的直方图及发展趋势线.(注:趋势线由Excel系统根据数据自动生成,趋势线中的y表示GDP,x表示年数)
2004﹣2018年中美两国国内生产总值(GDP,单位:万亿美元)直方图及发展趋势线
依据【资料】中所提供的信息,可以推算出中国的GDP要超过美国,至少要到( )
A.2052年 B.2038年 C.2037年 D.2034年
解:由图表中美GDP趋势线,要使得中国的GDP要超过美国,则有
0.86x+0.468>0.53x+11.778
解得x>
∵x为正整数
∴x≥35
∴中国的GDP要超过美国,至少要到2038年.
故选:B.
6.周末,小明带200元去图书大厦,下表记录了他全天的所有支出,其中小零食支出的金额不小心被涂黑了,如果每包小零食的售价为15元,那么小明可能剩下多少元?( )
支出 早餐 购买书籍 公交车票 小零食
金额(元) 20 140 5
A.5 B.10 C.15 D.30
解:设小明买了x包小零食,依题意得:
小明剩下的人民币可以表示:200﹣20﹣140﹣5﹣15x,
整理得:(35﹣15x)元﹣﹣﹣﹣﹣﹣①
0<20+140+5+15x<200,
解得:0<x<,
又∵x是取正整数,
∴x的取值为1或2,
(Ⅰ)当x=1时代入①得:35﹣15x=35﹣15×1=20元,
(Ⅱ)当x=2时代入①得:35﹣15x=35﹣15×2=5元.
从A、B、C、D四个选项中,符合题意只有A答案.
故选:A.
7.某项球类规则达标测验,规定满分100分,60分及格,模拟考试与正式考试形式相同,都是25道选择题,每题答对记4分,答错或不答记0分.并规定正式考试中要有80分的试题就是模拟考试中的原题.假设某人在模拟考试中答对的试题,在正式考试中仍能答对,某人欲在正式考试中确保及格,则他在模拟考试中,至少要得( )
A.80分 B.76分 C.75分 D.64分
解:设在模拟考试中至少要得x分
由题意列式
解得x≥80.即某人欲在正式考试中确保及格,则他在模拟考试中至少要得80分.
故选:A.
8.某药液的说明书上,贴有如图所示的标签,则一次性服用这种药品的剂量范围是( )
A.10mg~20mg B.15mg~30mg C.15mg~20mg D.10mg~30mg
解:依题意得:一次用药剂量的最大值===30mg
一次用药剂量的最小者===10mg
故:一次性服用这种药品的剂量范围是10mg~30mg
故选:D.
9.百货商场有一种商品的合格率为97%,已知该商品有400件,请问该商场至少还需准备( )件商品供消费者更换.
A.9个 B.15个 C.12个 D.13个
解:设至少还准备x件商品供消费者更换,
依题意可得(400+x)×97%≥400
解得:x≥12,又因为x取整数,则x最小是13.
故选:D.
10.奥运会十米跳台跳水比赛的规则是:每个跳水运动员有十次跳水机会,每次的最高得分是100分,按最终得分决定名次.某运动员前7次跳水共得580分,如果他要打破850分的奥运会纪录,第8次跳水至少要高于( )
A.60分 B.70分 C.80分 D.100分
解:设不能少于x分,
由题意得,580+x+100+100>850,
解得:x>70,
即第8次跳水不能少于70分.
故选:B.
二.填空题(共5小题)
11.不等式x+2>3x﹣4的解集是 x<3 .
解:移项,得x﹣3x>﹣4﹣2,
合并同类项,得﹣2x>﹣6,
化系数为1,得 x<3,
故答案为x<3.
12.如果关于x的不等式(a﹣1)x>a+5和2x>4的解集相同,则a的值为 7 .
解:由2x>4得x>2,
∵两个不等式的解集相同,
∴由(a﹣1)x>a+5可得x>,
∴=2,
解得a=7.
故答案为:7.
13.若不等式3x﹣m≤0的正整数解是1,2,3,则m的取值范围是 9≤m<12 .
解:不等式3x﹣m≤0的解集是x≤,
∵正整数解是1,2,3,
∴m的取值范围是3≤<4即9≤m<12.
故答案为:9≤m<12.
14.若关于x的不等式2x﹣3a+2≥0的最小整数解为5,则实数a的取值为 <a≤4
解:解不等式2x﹣3a+2≥0得x≥,
∵不等式的最小整数解为5,
∴4≤5,
∴<a≤4,
故答案为:<a≤4.
15.用不等式表示语句“a与b的差不大于﹣2”为 a﹣b≤﹣2 .
解:“a与b的差不大于﹣2”用不等式表示为:a﹣b≤﹣2.
故答案为:a﹣b≤﹣2.
三.解答题(共5小题)
16.已知不等式x﹣2>x与ax﹣3>2x的解集相同,求a的值.
解:解不等式x﹣2>x得,x<﹣;
由不等式ax﹣3>2x得,(a﹣2)x>3,
∵两不等式的解集相同,
∴a﹣2<0,
∴x<,
∴=﹣,解得a=.
17.阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
如果一个不等式(含有不等号的式子)中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式.
求绝对值不等式|x|>3的解集(满足不等式的所有解).
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论,绝对值不等式|x|>3的解集为:x<﹣3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 x<﹣1或x>1 ;
②|x|<2.5的解集是 ﹣2.5<x<2.5 .
(2)求绝对值不等式|x﹣3|+5>9的解集.
(3)直接写出不等式x2>4的解集是 x<﹣2或x>2. .
解:(1)根据阅读材料可知:
①|x|>1的解集是x<﹣1或x>1;
②|x|<2.5的解集是﹣2.5<x<2.5.
故答案为:x<﹣1或x>1;﹣2.5<x<2.5.
(2)|x﹣3|+5>9
|x﹣3|>4
∴x﹣3<﹣4或x﹣3>4
解得x<﹣1或x>7;
(3)x2>4
解得x<﹣2或x>2.
故答案为:x<﹣2或x>2.
18.如果不等式3x﹣m≤0的正整数解是1,2,3,那么m的范围是什么?
解:先求出不等式的解集为x≤,
又它的正整数解只有1,2,3,
如图:
说明3≤<4,
求得9≤m<12.
19.已知不等式3x﹣a≤0的正整数解恰是1,2,3,求a的取值范围.
解:3x﹣a≤0,
移项得,3x≤a,
系数化为1得,x≤.
∵不等式3x﹣a≤0的正整数解恰是1,2,3,
∴3≤x<4,
∴3≤<4时,即9≤a<12时,不等式3x﹣a≤0的正整数解恰是1,2,3.
故a的取值范围是9≤a<12.
20.某水果店以每千克6元的价格购进一批水果,由于销售状况良好,该店又购进一些同一种水果,第二次进货价格比第一次每千克便宜了1元,已知两次一共进货600千克.
(1)若该水果店两次进货的总价格不超过3200元,求第一次至多购进水果多少千克?
(2)在(1)的条件下,以第一次购进最大重量时的数量进货,在销售过程中,第一次购进的水果有3%的损耗,其售价比其进价多2a元,第二次购进的水果有5%的损耗,其售价比其进价多a元,该水果店希望售完两批水果后获利31.75%,求a的值.
解:(1)设第一次购进水果x千克,
根据题意,得:6x+5(600﹣x)≤3200,
解得:x≤200,
答:第一次至多购进水果200千克;
(2)第一次至多购进水果200千克,则第二次购进400千克,根据题意,得:
(6+2a)×200(1﹣3%)﹣200×6+(5+a)×400(1﹣5%)﹣400×5=3200×31.75%,
解得:a=1.5
故a的值为1.5.
_21?????????è?????(www.21cnjy.com)_
