7.6立方根(第2课时) 课件(共16张PPT)
文档属性
| 名称 | 7.6立方根(第2课时) 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 17:38:24 | ||
图片预览



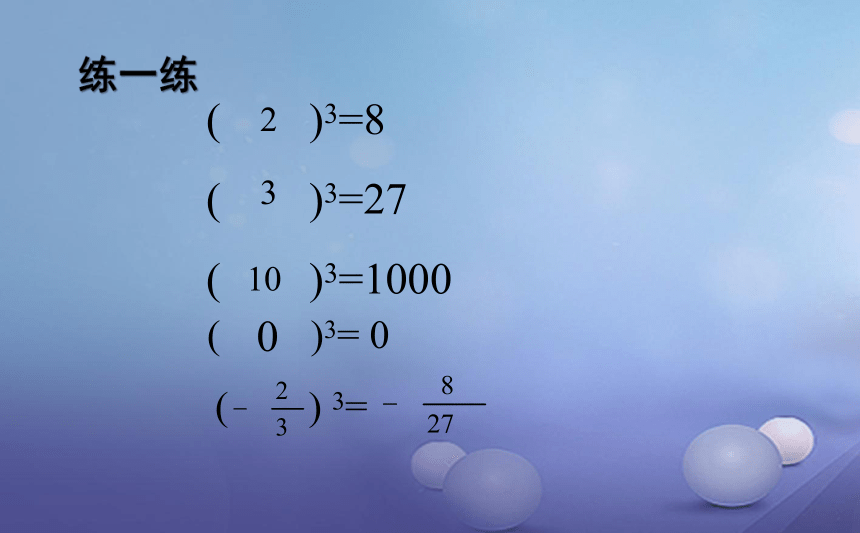



文档简介
(共16张PPT)
八年级下册
7.6
立方根
【学习目标】
1.了解立方根的概念,能够用根号表示一个数的立方根;
2.能用类比平方根的方法学习立方根及开立方运算,并区分立方根与平方根的不同.
【重
点】立方根的概念和求法.
【难
点】立方根与平方根的区别.
64的算术平方根是
(
)
的平方根是(
)
3.
若a的平方根只有一个,那么a=(
)
若数b
的一个平方根是1.2,那么b
的另一个平方根是
(
)
5.
的算术平方根(
)
8
0
-1.2
3
练一练
(
)3=8
(
)3=27
(
)3=1000
2
3
10
0
(
)3=
0
(
)
3=
练一练
情境引入
探究活动任务一:
了解立方根的概念
阅读课本第64页,解决下列问题.
1.什么叫做a的立方根?用式子如何描述a的立方根?
如果一个数的立方等于a,这个数就叫做a的____.(或___
).换句话说,如果
,那么x叫做a的立方根或三次方根.
记作:
.读作“
”,其中a是
,3是____,且根指数3
省略(填能或不能),否则与平方根混淆.
2.什么叫开立方?它与立方有何关系?
学习与探究
任务二:根据立方根的意义填空,看看正数、0、负数的立方根各有什么特点?
因为
,所以8的立方根是(
);
因为
=0.125,所以0.125的立方根是(
);
因为
=0,所以0的立方根是(
);
因为
=-8,所以-8的立方根是(
).
思考:(1)正数的立方根是_____数,负数的立方根是_____数,0的立方根是_______.
1、求出下列各数的立方根:
⑴
⑵
0.216
⑶
0
⑷
2、求下列各式的值:
(1)
(2)
(3)
任务三:
读课本65页的例题解法,完成1、2题,自主完成,组内交流。
1.因为
所以
_____
因为
,所以
_____
.
思考:
针对上面题目的特点,你能用一个式子来表示其中的规律吗?小组讨论交流.
任务四:知识延伸
三、问题交流:
⑴交换导学案看一看,欣赏他人作业之美,同时发现自己和他人之不足。
⑵组长组织组内各位同学说一说自己出现的困惑,然后总结小组内不能解决的问题和一些发现,
展示提升(展示不能解决的问题,接受任务,小组作好准备哦!)
你能说出数的平方根与数的立方根有什么不同吗?
1.
判断正误:
(1)25的立方根是5;(
)
(2)互为相反数的两个数,它们的立方根也互为相反数;(
)
(3)任何数的立方根只有一个;(
)
(4)如果一个数的平方根与其立方根相同,则这个数是1;(
)
(5)如果一个数的立方根是这个数的本身,那么这个数一定
是零;(
)
(6)一个数的立方根不是正数就是负数.(
)
(7)–64没有立方根.(
)
2.填空题:
(1)64的平方根是________立方根是________.
(2)
的立方根是________;
是_______的立方根.
当堂达标
1.
的平方根与-8的立方根之和是(
)
A.0
B.-4
C.0或-4
D.4
2.若
(
)
A.-
B.
C.
D.-
3.如果
,那么a是(
)
A.±1
B.1,0
C.±1,0
D.以上都不对
4.
的立方根是
,平方根是_______。
5、若
,则x=______.
随堂练习
6、求下列各数的立方根
⑴
⑵
⑶
7、求下列各式中的的值
⑴
⑵
⑶
8、将一个体积为216
的正方体分成等大的8个小正方体,求每个小正方体的表面积。
9、下列各题错在何处?
(1)
的立方根是3;
(2)
的立方根是±3。
①立方根的概念、性质.
方法归纳:根据乘方与开方的互逆关系求一个数的立方根。
②立方根与平方根有什么异同?(从定义,根的个数,表示方法及被开方数的取值范围方面来考虑。)
课堂小结
祝同学们学习进步!
八年级下册
7.6
立方根
【学习目标】
1.了解立方根的概念,能够用根号表示一个数的立方根;
2.能用类比平方根的方法学习立方根及开立方运算,并区分立方根与平方根的不同.
【重
点】立方根的概念和求法.
【难
点】立方根与平方根的区别.
64的算术平方根是
(
)
的平方根是(
)
3.
若a的平方根只有一个,那么a=(
)
若数b
的一个平方根是1.2,那么b
的另一个平方根是
(
)
5.
的算术平方根(
)
8
0
-1.2
3
练一练
(
)3=8
(
)3=27
(
)3=1000
2
3
10
0
(
)3=
0
(
)
3=
练一练
情境引入
探究活动任务一:
了解立方根的概念
阅读课本第64页,解决下列问题.
1.什么叫做a的立方根?用式子如何描述a的立方根?
如果一个数的立方等于a,这个数就叫做a的____.(或___
).换句话说,如果
,那么x叫做a的立方根或三次方根.
记作:
.读作“
”,其中a是
,3是____,且根指数3
省略(填能或不能),否则与平方根混淆.
2.什么叫开立方?它与立方有何关系?
学习与探究
任务二:根据立方根的意义填空,看看正数、0、负数的立方根各有什么特点?
因为
,所以8的立方根是(
);
因为
=0.125,所以0.125的立方根是(
);
因为
=0,所以0的立方根是(
);
因为
=-8,所以-8的立方根是(
).
思考:(1)正数的立方根是_____数,负数的立方根是_____数,0的立方根是_______.
1、求出下列各数的立方根:
⑴
⑵
0.216
⑶
0
⑷
2、求下列各式的值:
(1)
(2)
(3)
任务三:
读课本65页的例题解法,完成1、2题,自主完成,组内交流。
1.因为
所以
_____
因为
,所以
_____
.
思考:
针对上面题目的特点,你能用一个式子来表示其中的规律吗?小组讨论交流.
任务四:知识延伸
三、问题交流:
⑴交换导学案看一看,欣赏他人作业之美,同时发现自己和他人之不足。
⑵组长组织组内各位同学说一说自己出现的困惑,然后总结小组内不能解决的问题和一些发现,
展示提升(展示不能解决的问题,接受任务,小组作好准备哦!)
你能说出数的平方根与数的立方根有什么不同吗?
1.
判断正误:
(1)25的立方根是5;(
)
(2)互为相反数的两个数,它们的立方根也互为相反数;(
)
(3)任何数的立方根只有一个;(
)
(4)如果一个数的平方根与其立方根相同,则这个数是1;(
)
(5)如果一个数的立方根是这个数的本身,那么这个数一定
是零;(
)
(6)一个数的立方根不是正数就是负数.(
)
(7)–64没有立方根.(
)
2.填空题:
(1)64的平方根是________立方根是________.
(2)
的立方根是________;
是_______的立方根.
当堂达标
1.
的平方根与-8的立方根之和是(
)
A.0
B.-4
C.0或-4
D.4
2.若
(
)
A.-
B.
C.
D.-
3.如果
,那么a是(
)
A.±1
B.1,0
C.±1,0
D.以上都不对
4.
的立方根是
,平方根是_______。
5、若
,则x=______.
随堂练习
6、求下列各数的立方根
⑴
⑵
⑶
7、求下列各式中的的值
⑴
⑵
⑶
8、将一个体积为216
的正方体分成等大的8个小正方体,求每个小正方体的表面积。
9、下列各题错在何处?
(1)
的立方根是3;
(2)
的立方根是±3。
①立方根的概念、性质.
方法归纳:根据乘方与开方的互逆关系求一个数的立方根。
②立方根与平方根有什么异同?(从定义,根的个数,表示方法及被开方数的取值范围方面来考虑。)
课堂小结
祝同学们学习进步!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
