7.8实数 课件（共20张PPT）

(共20张PPT)
八年级下册
7.8.1
实数
知识回顾
1.什么是有理数？有理数怎样分类？
整数
分数
有理数
正有理数
负有理数
有理数
0
2.什么是无理数？带根号的数都是无理数吗？
无理数是无限不循环小数.
带根号的数不一定是无理数.
判断下列数哪些是有理数？哪些是无理数？
有理数是：
无理数是：
,
,
,
回顾：无理数一般有哪些形式?
（1）开不尽方的数是无理数。
（2）
及含有
的数是无理数
（3）有一定的规律，但不循环的无限小数是无理数。
把下列各数分别填入相应的集合内：
（相邻两个3之间的7的个数逐次加1）
有理数集合
无理数集合
试一试
定
义：
有理数和无理数统称为实数
即实数可以分为有理数和无理数
有理数
无理数
实数
实数
有理数
无理数
正有理数
负有理数
零
正无理数
负无理数
无限不循环小数
根据有理数分类，你会不会对实数进行分类?
有限小数或无限循环小数
按性质分类
正有理数
正无理数
负有理数
负无理数
实数
实数
正实数
负实数
按大小分类
练习
判断下列说法是否正确：
4）实数可以分为正实数和负实数两类
5）无理数包括正无理数、零、负无理数.
6）有理数都是有限小数。
…
（　　　）
…（　　　）
……………………（　　　）
1）无限小数都是无理数；
2）无理数都是无限小数；
3）正实数包括正有理数和正无理数；
……………………（　　　）
…………………（　　　）
………（　　　）
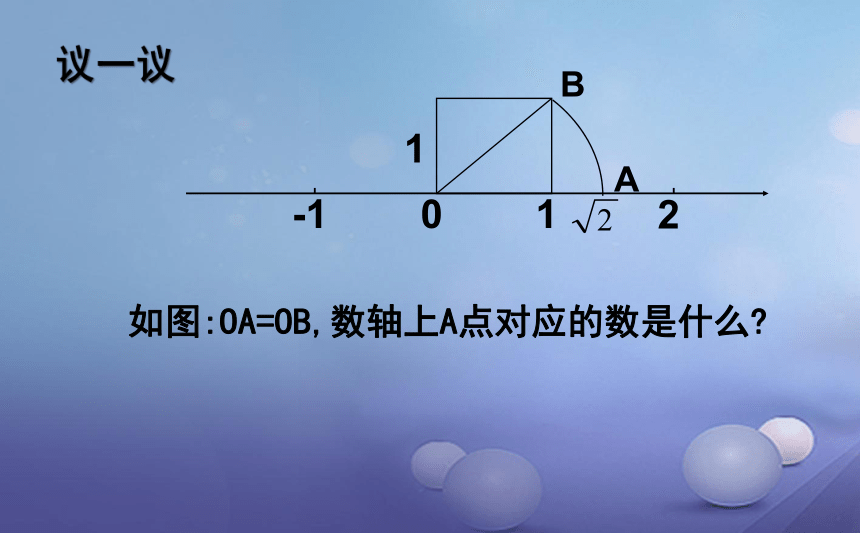
议一议
1
A
B
如图:OA=OB,数轴上A点对应的数是什么?
2
1
0
-1
在数轴上作出
的对应点.
0
1
2
3
-1
1
2
0
1
2
-1
-2
A
一个实数a
-1
-1
0
-1
1
0
-1
1
0
-1
3
1
0
-1
3
1
0
-1
3
3
1
3
0
1
3
-1
0
1
3
如果将所有有理数都标到数轴上,那么数轴被填满了吗?
实数与数轴上的点的对应关系：
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。
Ａ
-2
-1
0
1
2
实数
a
数=>点
数<=点
同样的，在数轴上,右边的点表示的数比左边的点表示的数大.
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例1：
例题精讲
2.a是一个实数,它的相反数是
　　
绝对值是
　　
当a≠0时，它的倒数是
1.
的绝对值是
练一练
例2
比较下列各组数中两个数的大小：
（1）3.14与π；
（2）
与
.
解：（1）∵π≈3.141，
∴3.14<π.
（2）∵
≈-1.732，
≈-1.442
∴
<
例题精讲
1、求下列各数的相反数、倒数和绝对值：
2
2
-7
7
随堂练习
2、a、b互为相反数，c与d互为倒数则a+1+b+cd=
。
3、实数a,b,c,d在数轴上的对应点如图所示，则
它们从小到大的顺序是
。
c
d
0
b
a
其中：
2
ca+b
-d-c
b-c
a-d
这节课你有什么收获？
你对本节课的内容还有哪些疑问？
课堂小结
到目前为止，你认识了哪些数？
自然数
分数
负数
有理数
小数
负整数
正整数
零
有限小数
无限不循环小数-无理数
负有理数
祝同学们学习进步！