【高频易错题汇编】7.3 图形的平移 (含解析)
文档属性
| 名称 | 【高频易错题汇编】7.3 图形的平移 (含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 527.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
7.3 图形的平移 高频易错题集
一.选择题(共10小题)
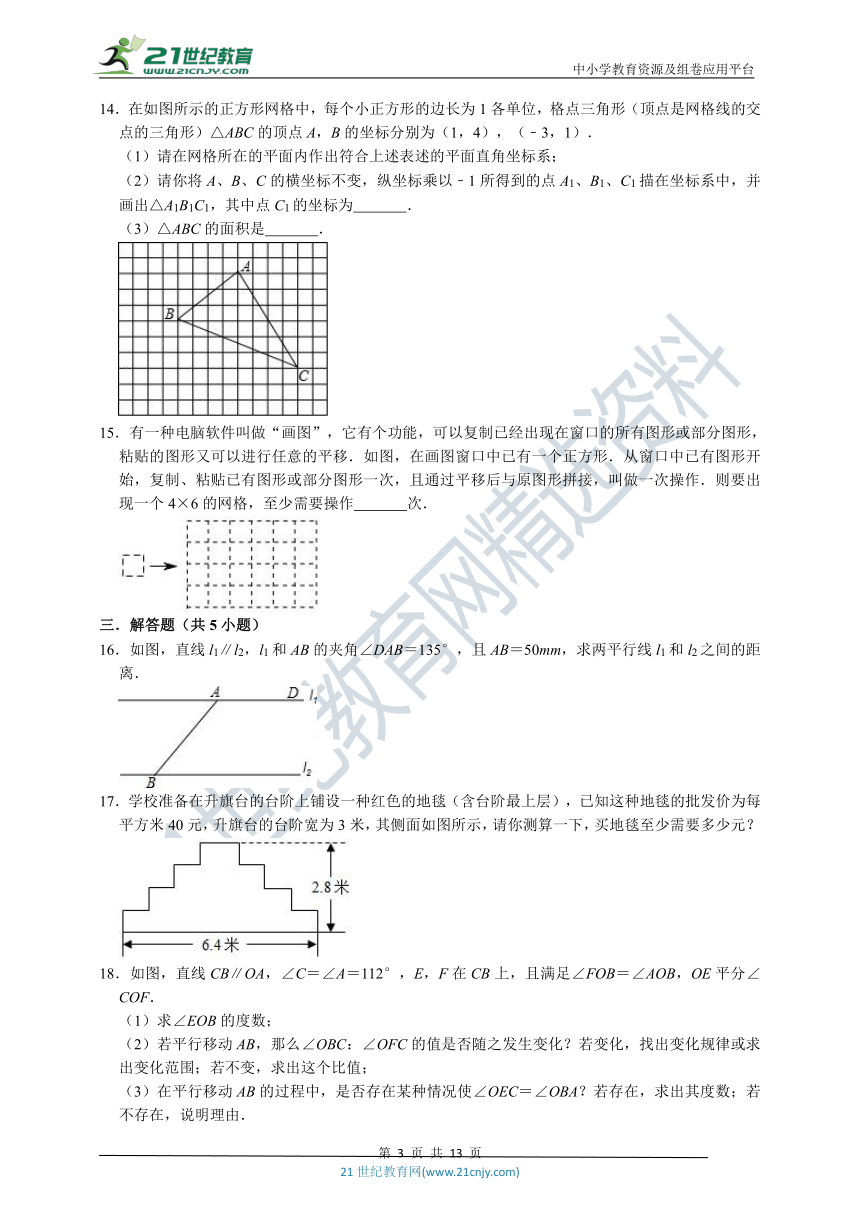
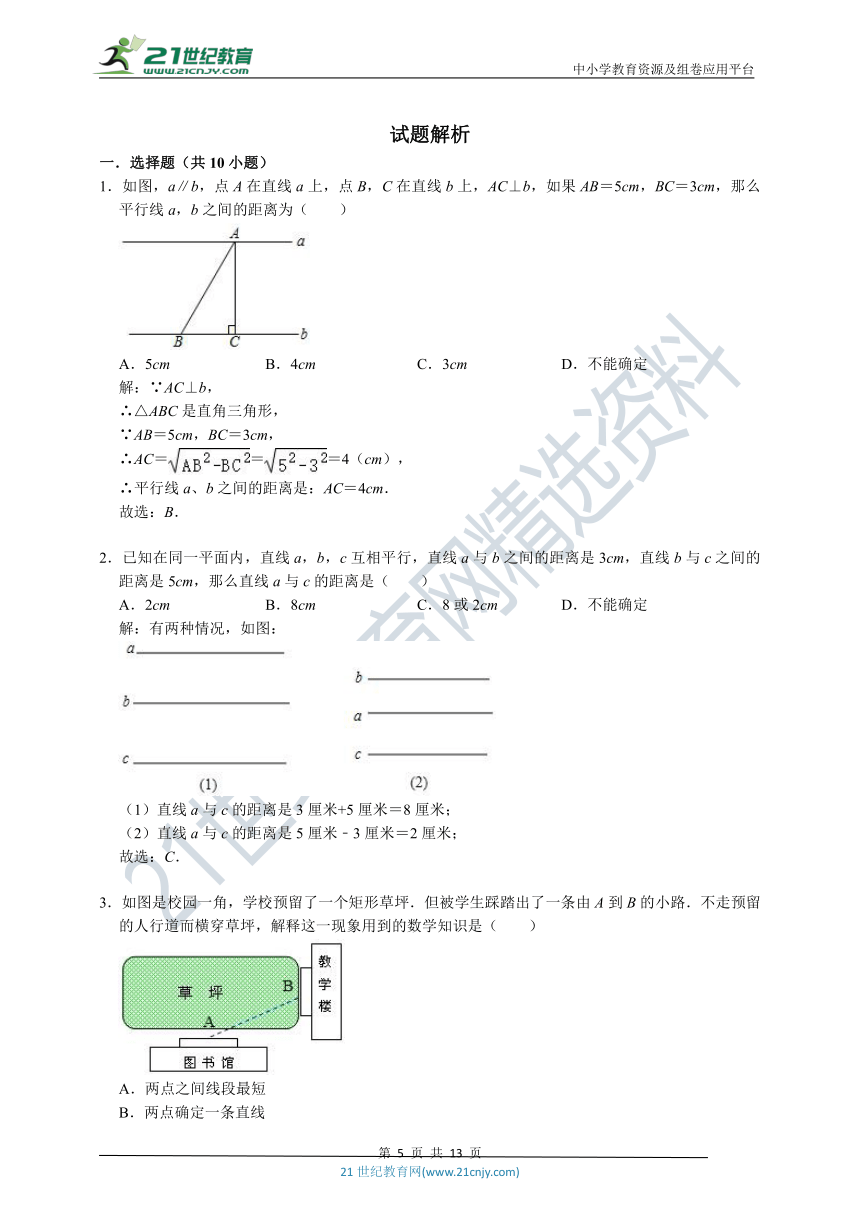
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
3.如图是校园一角,学校预留了一个矩形草坪.但被学生踩踏出了一条由A到B的小路.不走预留的人行道而横穿草坪,解释这一现象用到的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.两平行线间的距离处处相等
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.在下列图案中,不能用平移得到的图案是( )
A. B. C. D.
6.通过平移图中的吉祥物“海宝”得到的图形是( )
A. B. C. D.
7.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
8.下列生活中的各个现象,属于平移变换现象的是( )
A.冷水加热过程中小气泡上升称为大气泡
B.拉开抽屉
C.时钟上分针的运动
D.随风飘动的树叶在空中的运动
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=4,则△ABC移动的距离是( )
A.2 B.2 C.1 D.4﹣2
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
A.75° B.105° C.130° D.155°
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
12.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 m2.
13.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为 .
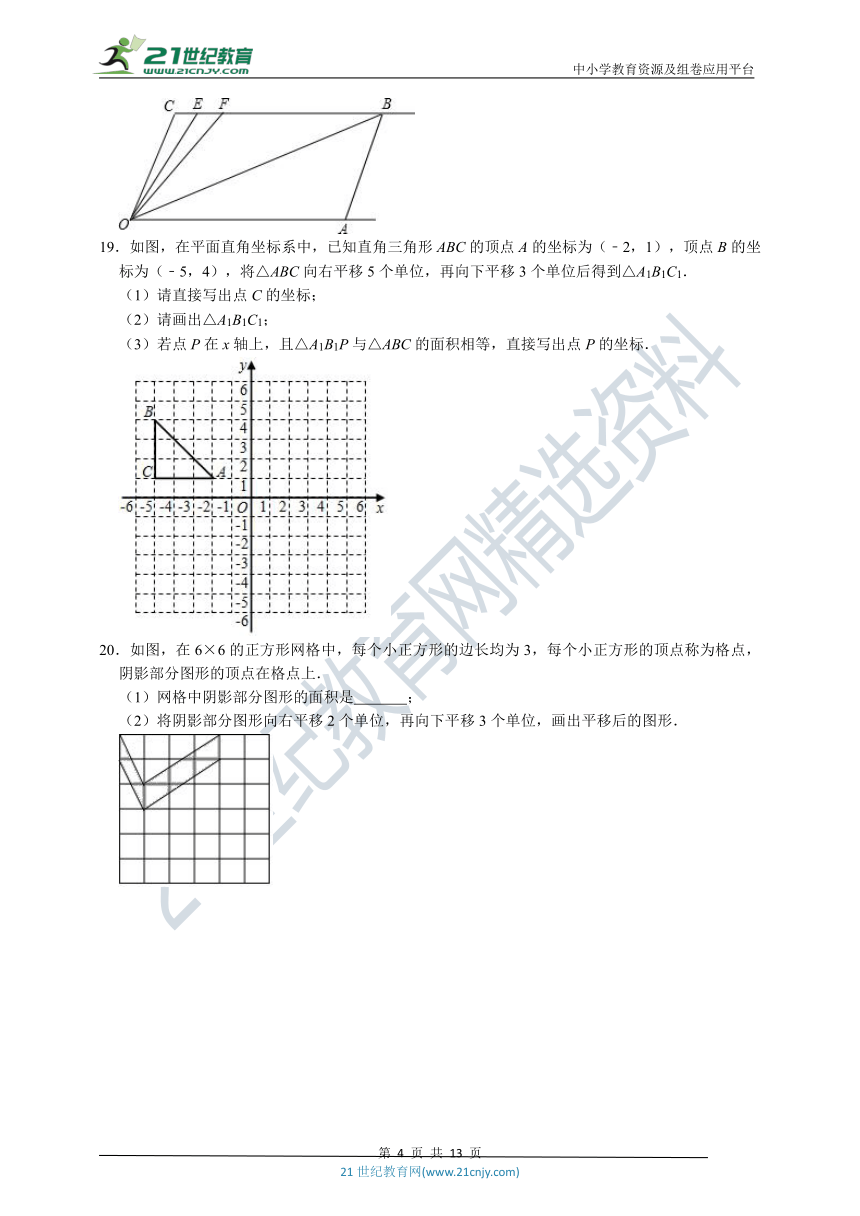
14.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
15.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作 次.
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
17.学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示,请你测算一下,买地毯至少需要多少元?
18.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
19.如图,在平面直角坐标系中,已知直角三角形ABC的顶点A的坐标为(﹣2,1),顶点B的坐标为(﹣5,4),将△ABC向右平移5个单位,再向下平移3个单位后得到△A1B1C1.
(1)请直接写出点C的坐标;
(2)请画出△A1B1C1;
(3)若点P在x轴上,且△A1B1P与△ABC的面积相等,直接写出点P的坐标.
20.如图,在6×6的正方形网格中,每个小正方形的边长均为3,每个小正方形的顶点称为格点,阴影部分图形的顶点在格点上.
(1)网格中阴影部分图形的面积是 ;
(2)将阴影部分图形向右平移2个单位,再向下平移3个单位,画出平移后的图形.
试题解析
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
解:∵AC⊥b,
∴△ABC是直角三角形,
∵AB=5cm,BC=3cm,
∴AC===4(cm),
∴平行线a、b之间的距离是:AC=4cm.
故选:B.
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
3.如图是校园一角,学校预留了一个矩形草坪.但被学生踩踏出了一条由A到B的小路.不走预留的人行道而横穿草坪,解释这一现象用到的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.两平行线间的距离处处相等
解:从A地到B地有几条路可走,为了尽快到达,人们通常选择其中的直路,理由是两点之间线段最短,
故选:A.
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.在下列图案中,不能用平移得到的图案是( )
A. B. C. D.
解:A、两个图形的阴影部分不同,不能用平移得到,符合题意;
B、可由一个或2个简单图形平移得到,不符合题意;
C、可由一个或2个简单图形平移得到,不符合题意;
D、可由上下两个图形向右平移得到,不符合题意;
故选:A.
6.通过平移图中的吉祥物“海宝”得到的图形是( )
A. B. C. D.
解:A、B、C吉祥物“海宝”是原图形通过旋转得到的,因此不是平移,只有D符合要求,是平移.
故选:D.
7.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
解:身高1.65米的小明乘电梯从1楼上升到5楼,则此时小明的身高为1.65米,
故选:B.
8.下列生活中的各个现象,属于平移变换现象的是( )
A.冷水加热过程中小气泡上升称为大气泡
B.拉开抽屉
C.时钟上分针的运动
D.随风飘动的树叶在空中的运动
解:A.冷水加热过程中小气泡上升称为大气泡,不属于平移现象;
B.拉开抽屉,属于平移现象;
C.时钟上分针的运动,属于旋转现象;
D.随风飘动的树叶在空中的运动,不属于平移现象;
故选:B.
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=4,则△ABC移动的距离是( )
A.2 B.2 C.1 D.4﹣2
解:∵△ABC沿BC边平移到△DEF的位置,
∴AB∥DE,
∴△ABC∽△HEC,
∴=()2=,
∴EC:BC=1:,
∵BC=4,
∴EC=2,
∴BE=BC﹣EC=4﹣2.
故选:D.
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
A.75° B.105° C.130° D.155°
解:∵∠AOB沿着MN的方向平移一定距离后得∠CPD,
∴BO∥DP,
∴∠BON=∠DPN=50°,
∵∠AOM+∠AOB+∠BON=180°,
∴∠AOB=180°﹣25°﹣50°=105°.
故选:B.
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 7或17 cm.
解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
12.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 880 m2.
解:S=44×24﹣2×24×2﹣2×44+2×2×2=880(m2).
故答案为:880.
13.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为 30 .
解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的,
故内部五个小直角三角形的周长为AC+BC+AB=30.
故答案为:30.
14.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 (5,2) .
(3)△ABC的面积是 18 .
解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
故答案为:(5,2);
(3)△ABC的面积是×6×(3+3)=18.
故答案为:18.
15.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作 5 次.
解:如图,方法如下:
答:要出现一个4×6的网格,至少需要操作5次.
故答案为:5.
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
解:如图,过点A作AC⊥l2于点C,
∵直线l1∥l2,AC⊥l2,
∴∠DAC=90°,
∵∠DAB=135°,
∴∠BAC=∠DAB﹣∠DAC=45°,
∴∠ABC=45°,
∴∠BAC=∠ABC,
∴AC=BC,
在Rt△ABC中,AC2+BC2=AB2,
2AC2=502,
∴
∴两平行线l1和l2之间的距离为25.
17.学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示,请你测算一下,买地毯至少需要多少元?
解:如图:
利用平移线段,把台阶的横竖向上向左平移,构成一个矩形,长宽分别为6.4米,2.8米,
∴地毯的长度为6.4+2.8+2.8=12米,地毯的面积为12×3=36(平方米),
∴买地毯至少需要36×40=1440(元).
答:买地毯需要1440元.
18.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×68°=17°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣112°﹣17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
19.如图,在平面直角坐标系中,已知直角三角形ABC的顶点A的坐标为(﹣2,1),顶点B的坐标为(﹣5,4),将△ABC向右平移5个单位,再向下平移3个单位后得到△A1B1C1.
(1)请直接写出点C的坐标;
(2)请画出△A1B1C1;
(3)若点P在x轴上,且△A1B1P与△ABC的面积相等,直接写出点P的坐标.
解:(1)观察网格可得:
点C的坐标(﹣5,1);
(2)如图△A1B1C1为所画图形;
(3)∵点P在x轴上,且△A1B1P与△ABC的面积相等,
∴P(﹣2,0)或P(4,0).
20.如图,在6×6的正方形网格中,每个小正方形的边长均为3,每个小正方形的顶点称为格点,阴影部分图形的顶点在格点上.
(1)网格中阴影部分图形的面积是 36 ;
(2)将阴影部分图形向右平移2个单位,再向下平移3个单位,画出平移后的图形.
解:(1)阴影部分图形的面积是3×3+3×9=36,
故答案为:36;
(2)平移后的图形如图所示:
_21?????????è?????(www.21cnjy.com)_
7.3 图形的平移 高频易错题集
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
3.如图是校园一角,学校预留了一个矩形草坪.但被学生踩踏出了一条由A到B的小路.不走预留的人行道而横穿草坪,解释这一现象用到的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.两平行线间的距离处处相等
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
5.在下列图案中,不能用平移得到的图案是( )
A. B. C. D.
6.通过平移图中的吉祥物“海宝”得到的图形是( )
A. B. C. D.
7.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
8.下列生活中的各个现象,属于平移变换现象的是( )
A.冷水加热过程中小气泡上升称为大气泡
B.拉开抽屉
C.时钟上分针的运动
D.随风飘动的树叶在空中的运动
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=4,则△ABC移动的距离是( )
A.2 B.2 C.1 D.4﹣2
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
A.75° B.105° C.130° D.155°
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 cm.
12.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 m2.
13.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为 .
14.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
15.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作 次.
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
17.学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示,请你测算一下,买地毯至少需要多少元?
18.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
19.如图,在平面直角坐标系中,已知直角三角形ABC的顶点A的坐标为(﹣2,1),顶点B的坐标为(﹣5,4),将△ABC向右平移5个单位,再向下平移3个单位后得到△A1B1C1.
(1)请直接写出点C的坐标;
(2)请画出△A1B1C1;
(3)若点P在x轴上,且△A1B1P与△ABC的面积相等,直接写出点P的坐标.
20.如图,在6×6的正方形网格中,每个小正方形的边长均为3,每个小正方形的顶点称为格点,阴影部分图形的顶点在格点上.
(1)网格中阴影部分图形的面积是 ;
(2)将阴影部分图形向右平移2个单位,再向下平移3个单位,画出平移后的图形.
试题解析
一.选择题(共10小题)
1.如图,a∥b,点A在直线a上,点B,C在直线b上,AC⊥b,如果AB=5cm,BC=3cm,那么平行线a,b之间的距离为( )
A.5cm B.4cm C.3cm D.不能确定
解:∵AC⊥b,
∴△ABC是直角三角形,
∵AB=5cm,BC=3cm,
∴AC===4(cm),
∴平行线a、b之间的距离是:AC=4cm.
故选:B.
2.已知在同一平面内,直线a,b,c互相平行,直线a与b之间的距离是3cm,直线b与c之间的距离是5cm,那么直线a与c的距离是( )
A.2cm B.8cm C.8或2cm D.不能确定
解:有两种情况,如图:
(1)直线a与c的距离是3厘米+5厘米=8厘米;
(2)直线a与c的距离是5厘米﹣3厘米=2厘米;
故选:C.
3.如图是校园一角,学校预留了一个矩形草坪.但被学生踩踏出了一条由A到B的小路.不走预留的人行道而横穿草坪,解释这一现象用到的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.两平行线间的距离处处相等
解:从A地到B地有几条路可走,为了尽快到达,人们通常选择其中的直路,理由是两点之间线段最短,
故选:A.
4.如图所示,a∥b,直线a与直线b之间的距离是( )
A.线段PA的长度 B.线段PB的长度
C.线段PC的长度 D.线段CD的长度
解:由图可得,a∥b,AP⊥a,
∴直线a与直线b之间的距离是线段PA的长度,
故选:A.
5.在下列图案中,不能用平移得到的图案是( )
A. B. C. D.
解:A、两个图形的阴影部分不同,不能用平移得到,符合题意;
B、可由一个或2个简单图形平移得到,不符合题意;
C、可由一个或2个简单图形平移得到,不符合题意;
D、可由上下两个图形向右平移得到,不符合题意;
故选:A.
6.通过平移图中的吉祥物“海宝”得到的图形是( )
A. B. C. D.
解:A、B、C吉祥物“海宝”是原图形通过旋转得到的,因此不是平移,只有D符合要求,是平移.
故选:D.
7.小明身高1.65米,他乘坐电梯从1楼到5楼,此时他的身高为( )米.
A.1.55 B.1.65 C.1.78 D.1.85
解:身高1.65米的小明乘电梯从1楼上升到5楼,则此时小明的身高为1.65米,
故选:B.
8.下列生活中的各个现象,属于平移变换现象的是( )
A.冷水加热过程中小气泡上升称为大气泡
B.拉开抽屉
C.时钟上分针的运动
D.随风飘动的树叶在空中的运动
解:A.冷水加热过程中小气泡上升称为大气泡,不属于平移现象;
B.拉开抽屉,属于平移现象;
C.时钟上分针的运动,属于旋转现象;
D.随风飘动的树叶在空中的运动,不属于平移现象;
故选:B.
9.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=4,则△ABC移动的距离是( )
A.2 B.2 C.1 D.4﹣2
解:∵△ABC沿BC边平移到△DEF的位置,
∴AB∥DE,
∴△ABC∽△HEC,
∴=()2=,
∴EC:BC=1:,
∵BC=4,
∴EC=2,
∴BE=BC﹣EC=4﹣2.
故选:D.
10.如图,点O在MN上,把∠AOB沿着MN的方向平移一定距离后得∠CPD.已知∠AOM=25°,∠DPN=50°,则∠AOB的大小是( )
A.75° B.105° C.130° D.155°
解:∵∠AOB沿着MN的方向平移一定距离后得∠CPD,
∴BO∥DP,
∴∠BON=∠DPN=50°,
∵∠AOM+∠AOB+∠BON=180°,
∴∠AOB=180°﹣25°﹣50°=105°.
故选:B.
二.填空题(共5小题)
11.设AB,CD,EF是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD的距离是5cm,则AB与EF的距离等于 7或17 cm.
解:分两种情况:
①当EF在AB,CD之间时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12﹣5=7(cm).
②当AB,CD在EF同侧时,如图:
∵AB与CD的距离是12cm,EF与CD的距离是5cm,
∴EF与AB的距离为12+5=17(cm).
综上所述,EF与AB的距离为7cm或17cm.
故答案为:7或17.
12.如图,有一块长为44m、宽为24m的长方形草坪,其中有三条直道将草坪分为六块,则分成的六块草坪的总面积是 880 m2.
解:S=44×24﹣2×24×2﹣2×44+2×2×2=880(m2).
故答案为:880.
13.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为 30 .
解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的,
故内部五个小直角三角形的周长为AC+BC+AB=30.
故答案为:30.
14.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(﹣3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以﹣1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 (5,2) .
(3)△ABC的面积是 18 .
解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
故答案为:(5,2);
(3)△ABC的面积是×6×(3+3)=18.
故答案为:18.
15.有一种电脑软件叫做“画图”,它有个功能,可以复制已经出现在窗口的所有图形或部分图形,粘贴的图形又可以进行任意的平移.如图,在画图窗口中已有一个正方形.从窗口中已有图形开始,复制、粘贴已有图形或部分图形一次,且通过平移后与原图形拼接,叫做一次操作.则要出现一个4×6的网格,至少需要操作 5 次.
解:如图,方法如下:
答:要出现一个4×6的网格,至少需要操作5次.
故答案为:5.
三.解答题(共5小题)
16.如图,直线l1∥l2,l1和AB的夹角∠DAB=135°,且AB=50mm,求两平行线l1和l2之间的距离.
解:如图,过点A作AC⊥l2于点C,
∵直线l1∥l2,AC⊥l2,
∴∠DAC=90°,
∵∠DAB=135°,
∴∠BAC=∠DAB﹣∠DAC=45°,
∴∠ABC=45°,
∴∠BAC=∠ABC,
∴AC=BC,
在Rt△ABC中,AC2+BC2=AB2,
2AC2=502,
∴
∴两平行线l1和l2之间的距离为25.
17.学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示,请你测算一下,买地毯至少需要多少元?
解:如图:
利用平移线段,把台阶的横竖向上向左平移,构成一个矩形,长宽分别为6.4米,2.8米,
∴地毯的长度为6.4+2.8+2.8=12米,地毯的面积为12×3=36(平方米),
∴买地毯至少需要36×40=1440(元).
答:买地毯需要1440元.
18.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
解:(1)∵CB∥OA,
∴∠AOC=180°﹣∠C=180°﹣112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×68°=17°,
∴∠OEC=180°﹣∠C﹣∠COE=180°﹣112°﹣17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
19.如图,在平面直角坐标系中,已知直角三角形ABC的顶点A的坐标为(﹣2,1),顶点B的坐标为(﹣5,4),将△ABC向右平移5个单位,再向下平移3个单位后得到△A1B1C1.
(1)请直接写出点C的坐标;
(2)请画出△A1B1C1;
(3)若点P在x轴上,且△A1B1P与△ABC的面积相等,直接写出点P的坐标.
解:(1)观察网格可得:
点C的坐标(﹣5,1);
(2)如图△A1B1C1为所画图形;
(3)∵点P在x轴上,且△A1B1P与△ABC的面积相等,
∴P(﹣2,0)或P(4,0).
20.如图,在6×6的正方形网格中,每个小正方形的边长均为3,每个小正方形的顶点称为格点,阴影部分图形的顶点在格点上.
(1)网格中阴影部分图形的面积是 36 ;
(2)将阴影部分图形向右平移2个单位,再向下平移3个单位,画出平移后的图形.
解:(1)阴影部分图形的面积是3×3+3×9=36,
故答案为:36;
(2)平移后的图形如图所示:
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
