【高频易错题汇编】12.2 证明(含解析)
文档属性
| 名称 | 【高频易错题汇编】12.2 证明(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 370.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
12.2 证明 高频易错题集
一.选择题(共10小题)
1.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
2.在一次1500米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,
我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )
A.甲 B.乙 C.丙 D.丁
3.某校七年级、八年级的学生人数相同,九年级的学生人数是八年级学生人数的,已知七年级的男生人数与八年级的女生人数相同,九年级男生人数占三个年级男生人数的,那么三个年级的男生与女生的比为( )
A. B. C. D.
4.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初二(8)班举办了“乐知杯古诗词”大赛.现有小璟、小桦、小花三位同学进入了最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.如表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,下列说法正确的是( )
第一轮 第二轮 第三轮 第四轮 第五轮 第六轮 最后得分
小璟 a a 26
小桦 a b c 11
小花 b b 11
A.小璟可能有一轮比赛获得第二名
B.小桦有三轮比赛获得第三名
C.小花可能有一轮比赛获得第一名
D.每轮比赛第一名得分a为5
5.有一种“扫雷”游戏如图,方格内的数字表示与它相邻的方格内总共有的地雷数,例如:右下角的数字1表示A、B、C中只有一个地雷;通过推理,请判断?处应填的数字是.( )
2 3
3 A B
1 ? C 1
A.5 B.4 C.3 D.2
6.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
7.如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
A.50秒 B.45秒 C.40秒 D.35秒
8.广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表:若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短线路距离是( )
A.20.6 B.21 C.22 D.23
9.用:0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只使用一次),然后把所得的数相加,它们的和不可能是( )
A.36 B.117 C.115 D.153
10.甲,乙,丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲,乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
二.填空题(共5小题)
11.某班对思想品德、历史、地理三门课程的选考情况进行调研,数据如下:
科目 思想品德 历史 地理
选考人数(人) 20 13 18
其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有 人;该班至少有学生 人.
12.学校广播室要从八年级(2)班选一名广播员,小明、小华和小英普通话都不相上下,并且都争着要去.老师决定用抽签的办法确定,结果三个人都争着先抽,以为第一个抽签的人抽中的可能性大一些; 这时,小华从兜里拿出两枚一元的硬币,并说将两枚硬币同时向上抛出,如果两个都是正面朝上,小明去;如果两个都是反面朝上,小英去;如果两个一正一反,小华自己去.那么,你认为 (填“老师”或“小华”)的办法公平合理,理由是 .
13.绕湖的一周是24千米,小张和小王从湖边某一地点同时出发,反向而行,小王以每小时4千米速度每走60分钟后休息5分钟;小张以每小时6千米速度每走50分钟后休息10分钟,则两人出发后 分钟后第一次相遇.
14.重庆一中秉持“尊重自由、激发自觉”的教育理念,开展了丰富多彩的第二课堂及各种有趣有益的竞赛活动.其中“小棋王”争霸赛得到同学们的踊跃参与,经过初选、复试最后十位同学进入决赛这十位同学进行单循环比赛(每两人均赛一局),胜一局得2分、平局得1分、负一局得0分,最后按照每人的累计得分的多少进行排名,得分最高者就是第一名,以此类推.赛完后发现每人最后得分均不相同,第一名和第二名的同学均没负一局,他们两人的得分之和比第三名同学多20分,第四名同学的得分刚好是最后四名同学得分的总和,则第五名的同学得分为 分.
15.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块已确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)
三.解答题(共4小题)
16.某次数学竞赛中有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个是正确的.如表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 第二题 第三题 第四题 第五题 得分
甲 C C A B B 4
乙 C C B B C 3
丙 B C C B B 2
丁 B C C B A
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可)
17.甲、乙、丙三人中一个是教师,一个是护士.一个是工人.现在只知道丙比工人年龄大,甲和护士不同岁,护士比乙年龄小.请你猜猜他们当中谁是教师,并说明理由.
18.阅读以下材料,并解答以下问题.
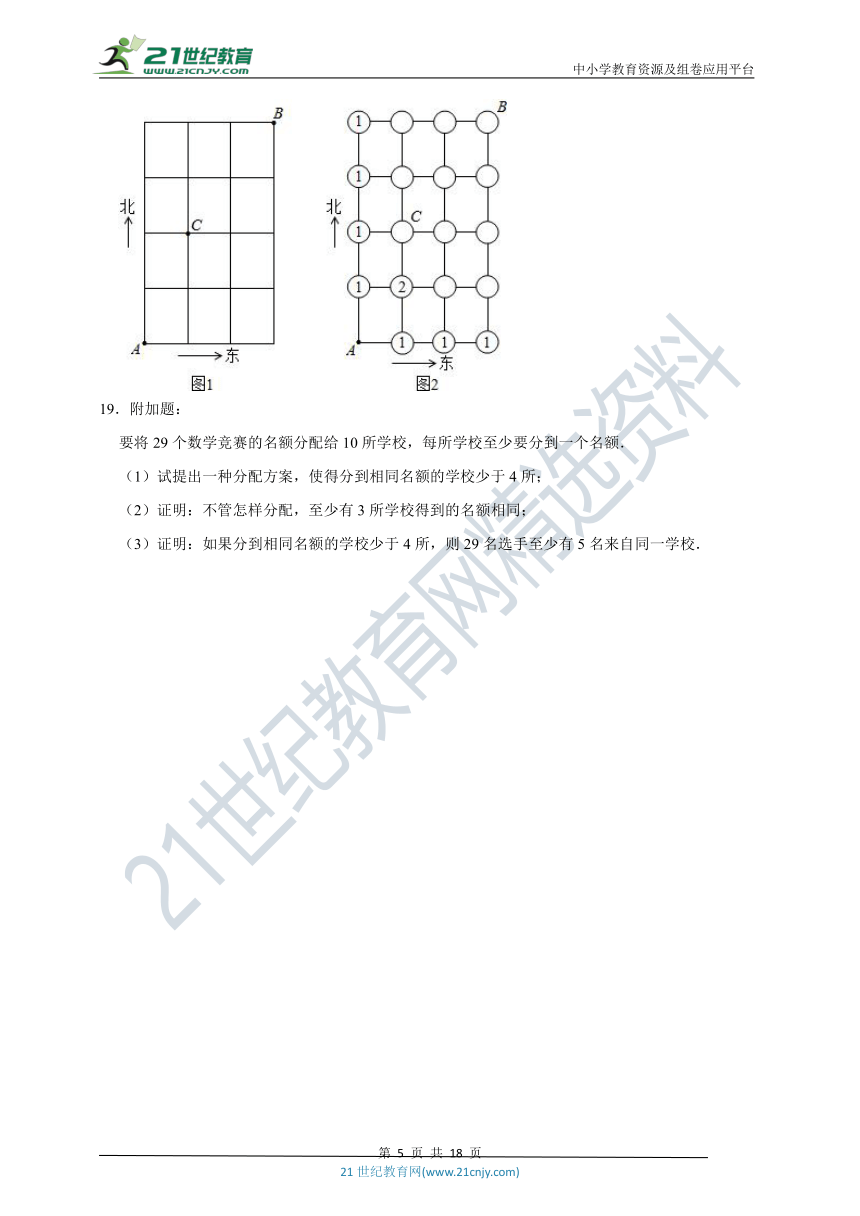
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?
19.附加题:
要将29个数学竞赛的名额分配给10所学校,每所学校至少要分到一个名额.
(1)试提出一种分配方案,使得分到相同名额的学校少于4所;
(2)证明:不管怎样分配,至少有3所学校得到的名额相同;
(3)证明:如果分到相同名额的学校少于4所,则29名选手至少有5名来自同一学校.
试题解析
一.选择题(共10小题)
1.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
解:设容易题有x道,中档题有y道,难题有z道,
由题意得,,
①×2﹣②得,z﹣x=20,
所以,难题比容易题多20道.
故选:B.
2.在一次1500米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,
我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )
A.甲 B.乙 C.丙 D.丁
解:根据分析,知
第一名应是乙.
故选:B.
3.某校七年级、八年级的学生人数相同,九年级的学生人数是八年级学生人数的,已知七年级的男生人数与八年级的女生人数相同,九年级男生人数占三个年级男生人数的,那么三个年级的男生与女生的比为( )
A. B. C. D.
解:设七年级总人数为x,则八年级总人数为x,九年级总人数为x;
设七年级男生人数为a,则女生人数为x﹣a;八年级女生人数为a,男生人数为x﹣a;
设九年级男生人数为b,则女生人数为x﹣b,
∵九年级男生人数占三个年级男生人数的,
∴三个年级男生人数为5b;=,
∴x=4b,
∵三个年级女生总人数为x﹣a+a+x﹣b=×4b﹣b=,
∴三个年级的男生与女生的比为5b:=,
故选:D.
4.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初二(8)班举办了“乐知杯古诗词”大赛.现有小璟、小桦、小花三位同学进入了最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.如表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,下列说法正确的是( )
第一轮 第二轮 第三轮 第四轮 第五轮 第六轮 最后得分
小璟 a a 26
小桦 a b c 11
小花 b b 11
A.小璟可能有一轮比赛获得第二名
B.小桦有三轮比赛获得第三名
C.小花可能有一轮比赛获得第一名
D.每轮比赛第一名得分a为5
解:由题可知:(a+b+c)×6=26+11+11=48,其中a>b>c且a,b,c均为正整数.
∴a+b+c也是正整数,
∴a+b+c=8.
∵若每轮比赛第一名得分a为4,则最后得分最高为:4×6=24<26,
∴a>4,
∵又a>b>c,b+c最小取3,
∴4<a<6.
∴a=5,b=2,c=1,
∴每轮比赛第一名得分a为5,小璟5轮得第一,1轮得第三;小桦4轮得第三,1轮得第一,1轮得第二;小花5轮得第二,1轮得第三.
故选:D.
5.有一种“扫雷”游戏如图,方格内的数字表示与它相邻的方格内总共有的地雷数,例如:右下角的数字1表示A、B、C中只有一个地雷;通过推理,请判断?处应填的数字是.( )
2 3
3 A B
1 ? C 1
A.5 B.4 C.3 D.2
解:根据题意用是表示有地雷,用不表示没有地雷填表得:
是 是 2 3 是
3 不 是 不 是
1 是 ? 不 1
?的周围有两颗地雷,所以?处应填的数字是2.
故选:D.
6.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
解:若甲对,即只参加一项的人数大于14人,不妨假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.
故选:B.
7.如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
A.50秒 B.45秒 C.40秒 D.35秒
解:∵甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,
∴两车的速度为:=(m/s),
∵AB之间的距离为800米,BC为1000米,CD为1400米,
∴分别通过AB,BC,CD所用的时间为:=96(s),=120(s),=168(s),
∵这两辆汽车通过四个路口时都没有遇到红灯,
∴当每次绿灯亮的时间为50s时,∵=1,∴甲车到达B路口时遇到红灯,故A错误;
∴当每次绿灯亮的时间为45s时,∵=3,∴乙车到达C路口时遇到红灯,故B错误;
∴当每次绿灯亮的时间为40s时,∵=5,∴甲车到达C路口时遇到红灯,故C错误;
∴当每次绿灯亮的时间为35s时,∵=2,=6,=10,=4,=8,
∴这两辆汽车通过四个路口时都没有遇到红灯,故D正确;
则每次绿灯亮的时间可能设置为:35秒.
故选:D.
8.广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表:若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短线路距离是( )
A.20.6 B.21 C.22 D.23
解:按路线ACBDE传递的距离为:4+7+6+5=22.
按路线ACDBE传递的距离为:4+9+6+2=21.
按路线ABCDE传递的距离为:5+7+9+5=26.
按路线ABDCE传递的距离为:5+6+9+8.6=28.6.
按路线ADCBE传递的距离为:5+9+7+2=23.
按路线ADBCE传递的距离为:5+6+7+8.6=26.6.
所以按路线ACDBE传递的距离最短,最短线路是21.
故选:B.
9.用:0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只使用一次),然后把所得的数相加,它们的和不可能是( )
A.36 B.117 C.115 D.153
解:0+1+2+3+4+5+6+7+8=36,
2+3+4+5+6+17+80=117,
0+1+2+3+4+56+87=153,
故不能组成115.
故选:C.
10.甲,乙,丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲,乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
解:由题意,知:三场比赛的对阵情况为:
第一场:甲VS乙,丙当裁判;
第二场:乙VS丙,甲当裁判;
第三场:甲VS乙,丙当裁判;
第四场:甲VS丙,乙当裁判;
第五场:乙VS甲,丙当裁判;
或第一场:甲VS乙,丙当裁判;
第二场:甲VS丙,乙当裁判;
第三场:甲VS乙,丙当裁判;
第四场:乙VS丙,甲当裁判;
第五场:乙VS甲,丙当裁判;
由于输球的人下局当裁判,因此第二场输的人是丙.
故选:C.
二.填空题(共5小题)
11.某班对思想品德、历史、地理三门课程的选考情况进行调研,数据如下:
科目 思想品德 历史 地理
选考人数(人) 20 13 18
其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有 17 人;该班至少有学生 30 人.
解:思想品德共有20人选择,其中选历史的有3人,所以选思想品德而没有选历史的有17人;
根据题意可以列表为:
所以该班选了思想品德而没有选历史的有17人;该班至少有学生30人.
故答案为:17,30.
12.学校广播室要从八年级(2)班选一名广播员,小明、小华和小英普通话都不相上下,并且都争着要去.老师决定用抽签的办法确定,结果三个人都争着先抽,以为第一个抽签的人抽中的可能性大一些; 这时,小华从兜里拿出两枚一元的硬币,并说将两枚硬币同时向上抛出,如果两个都是正面朝上,小明去;如果两个都是反面朝上,小英去;如果两个一正一反,小华自己去.那么,你认为 老师 (填“老师”或“小华”)的办法公平合理,理由是 老师的办法中,三人的机会相等,而小华的办法中,三人机会不等 .
解:老师,
因为老师的办法,不管谁先抽均有的机会;
而小华的办法中,有正反,正正,反正,反反4种情况,
小明和小英的机会各占,而小华的机会占=,
即老师的办法中,三人的机会相等,而小华的办法中,三人机会不等,
故答案为:老师;老师的办法中,三人的机会相等,而小华的办法中,三人机会不等.
13.绕湖的一周是24千米,小张和小王从湖边某一地点同时出发,反向而行,小王以每小时4千米速度每走60分钟后休息5分钟;小张以每小时6千米速度每走50分钟后休息10分钟,则两人出发后 160 分钟后第一次相遇.
解:∵小王65分行4千米,小张60分行6×=5千米,
∴小王130分行8千米,小张120分行10千米,
∴小张130分行10+×10=11千米;
∴在130分时间里,俩人一共行19千米,余下5千米还用5÷(+)=30分.所以出发160分第一次相遇.
故答案为160.
14.重庆一中秉持“尊重自由、激发自觉”的教育理念,开展了丰富多彩的第二课堂及各种有趣有益的竞赛活动.其中“小棋王”争霸赛得到同学们的踊跃参与,经过初选、复试最后十位同学进入决赛这十位同学进行单循环比赛(每两人均赛一局),胜一局得2分、平局得1分、负一局得0分,最后按照每人的累计得分的多少进行排名,得分最高者就是第一名,以此类推.赛完后发现每人最后得分均不相同,第一名和第二名的同学均没负一局,他们两人的得分之和比第三名同学多20分,第四名同学的得分刚好是最后四名同学得分的总和,则第五名的同学得分为 11 分.
解:因为每场比赛产生的最大分值是2分,这次比赛一共进行了45场比赛,因此产生的分值的最大值是90分.因为个人的最高得分是18分,又因为第一名选手与第二名选手均没有负一局,可以得出第一名选手与第二名选手是平一局,这个说明第一名选手最多17分,第二名选手最多16分,因此第一、二名选手的得分的和的最多33分.
情形1:当他们的总分是33分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分13分,.假设第四名选手得分12分,最后四名选手的得分总和为12分,由90﹣33﹣12﹣12=20可知,第5名为11分,第6名为9分.
情形2:当他们的总分是33分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分13分,假设第四名选手得分11分,最后四名选手的得分总和为11分,可知第5名与第6名的分数和为22分,两人中必有高于11分,与假设矛盾;
情形3:假设第一、二名选手的得分的和是32分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分12分,.假设第四名选手得分11分,最后四名选手的得分总和为11分,可知第5名与第6名的分数和为24分,结果推出矛盾,
故第1名17分,第2名16分,第3名13分,第4名12分,第5名11分,第6名9分;
故答案为11
15.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块已确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 B、D、F、G .(请填入方块上的字母)
解:图乙中最左边的“1”和最右边的“1”,可得如下推断
由第三行最左边的“1”,可得它的上方必定是雷.
结合B下方的“2”,可得最左边的A、B对应的方格中有一个雷;
同理可得最右边的“4”周围4个方格中有3个雷,中间D、E对应方格中有一个雷;
由于B下方的“2”和第二行最右边的“2”,它们周围的雷已经够数,
所以C对应的方格肯定不是雷,如下图所示:
进行下一步推理:
因为C对应的方格不是雷,所以C下方“2”的左上、右上的方格,即B、D都是雷;
而B下方的“2”的周围的雷也已经够数,所以A对应的方格也不是雷.
因为D下方的“2”,它的周围的雷已经够数,可得E对应的方格不是雷,
根据F下方的“4”周围应该有4个雷,结合E不是雷,可得F、G对应的方格都是雷.
综上所述,A、C、E对应的方格不是雷,且B、D、F、G对应的方格是雷.
故答案为:B、D、F、G.
三.解答题(共4小题)
16.某次数学竞赛中有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个是正确的.如表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 第二题 第三题 第四题 第五题 得分
甲 C C A B B 4
乙 C C B B C 3
丙 B C C B B 2
丁 B C C B A
(1)则甲同学错的是第 五 题;
(2)丁同学的得分是 3 ;
(3)如果有一个同学得了1分,他的答案可能是 CACCC (写出一种即可)
解:(1)∵有5道选择题,每题1分,
甲、乙、丙各得4,3,2分,
观察表格可知:第二题选C和第四题选B,甲、乙、丙、丁四位同学都正确,
所以丙同学答对第二题和第四题,得2分;
第一题选C,甲和乙同学都正确,
所以乙同学答对了第一、第二、第四题,得3分;
通过第三题可知:
乙,丙同学选B,C都答错了,
所以选项A正确,
所以第三题选A;
通过第五题,乙、丙两位同学选C和B都错误,
所以选A正确,
所以甲同学错的是第五题;
故答案为:五;
(2)因为五个题的正确答案是:C、C、A、B、A,
所以丁同学答对了第二、四、五题,
所以丁同学得分是3分.
故答案为:3;
(3)如果有一个同学得了1分,他的答案可能是:C、A、C、C、C(答案不唯一).
故答案为:C、A、C、C、C.
17.甲、乙、丙三人中一个是教师,一个是护士.一个是工人.现在只知道丙比工人年龄大,甲和护士不同岁,护士比乙年龄小.请你猜猜他们当中谁是教师,并说明理由.
解:乙是教师,
理由如下:∵甲和护士不同岁,护士比乙年龄小,
∴甲、乙都不是护士,
∴丙是护士,
∵护士比工人年龄大,护士比乙年龄小,
∴乙不是工人,
∴乙是教师.
18.阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?
解:(1)∵完成从A点到B点必须向北走,或向东走,
∴到达A点以外的任意交叉点的走法数只能是与其相邻的南边交叉点和西边交叉点的数字之和,
故使用分类加法计数原理,由此算出从A点到达其余各交叉点的走法数,填表如图1.
答:从A点到B点的走法共有35种.
(2)方法一:可先求从A点到B点,并经过交叉点C的走法数,再用从A点到B点总走法数减去它,即得从A点到B点,但不经过交叉点C的走法数.
完成从A点出发经C点到B点这件事可分两步,先从A点到C点,再从C点到B点,
使用分类加法计数原理,算出从A点到C点的走法是3种,见图2;算出从C点到B点的走法为6种,见图3,再运用分步乘法计数原理,得到从A点经C点到B点的走法有3×6=18种.
∴从A点到B点但不经过C点的走法数为35﹣18=17种.
方法二:由于交叉点C道路施工,禁止通行,故视为相邻道路不通,可删除与C点紧相连的线段,运用分类加法计数原理,算出从A点到B点并禁止通过交叉点C的走法有17种.从A点到各交叉点的走法数见图4,
∴从A点到B点并禁止经过C点的走法数为35﹣18=17种.
(3)P(顺利开车到达B点)=.
答:任选一种走法,顺利开车到达B点的概率是.
19.附加题:
要将29个数学竞赛的名额分配给10所学校,每所学校至少要分到一个名额.
(1)试提出一种分配方案,使得分到相同名额的学校少于4所;
(2)证明:不管怎样分配,至少有3所学校得到的名额相同;
(3)证明:如果分到相同名额的学校少于4所,则29名选手至少有5名来自同一学校.
解:(1)满足要求的分配方案有很多,如:学校对应的名额可以分别是:1,1,1,2,2,2,3,3,7,7;
(2)假设没有3所学校得到相同的名额,而每校至少要有1名,则人数最少的分配方案是:每两所学校一组依次各得1,2,3,4,5个名额,总人数为2(1+2+3+4+5)=30,但现在只有29个名额,故不管如何分配,都至少有3所学校分得的名额相同;
(3)假设每所学校分得的名额都不超过4,并且每校的名额不少于1,则在分到相同名额的学校少于4所的条件下,10所学校派出的选手数最多不会超过3×4+3×3+3×2+1×1=28,这与选手总数是29矛盾,从而至少有一所学校派出的选手数不小于5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
12.2 证明 高频易错题集
一.选择题(共10小题)
1.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
2.在一次1500米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,
我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )
A.甲 B.乙 C.丙 D.丁
3.某校七年级、八年级的学生人数相同,九年级的学生人数是八年级学生人数的,已知七年级的男生人数与八年级的女生人数相同,九年级男生人数占三个年级男生人数的,那么三个年级的男生与女生的比为( )
A. B. C. D.
4.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初二(8)班举办了“乐知杯古诗词”大赛.现有小璟、小桦、小花三位同学进入了最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.如表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,下列说法正确的是( )
第一轮 第二轮 第三轮 第四轮 第五轮 第六轮 最后得分
小璟 a a 26
小桦 a b c 11
小花 b b 11
A.小璟可能有一轮比赛获得第二名
B.小桦有三轮比赛获得第三名
C.小花可能有一轮比赛获得第一名
D.每轮比赛第一名得分a为5
5.有一种“扫雷”游戏如图,方格内的数字表示与它相邻的方格内总共有的地雷数,例如:右下角的数字1表示A、B、C中只有一个地雷;通过推理,请判断?处应填的数字是.( )
2 3
3 A B
1 ? C 1
A.5 B.4 C.3 D.2
6.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
7.如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
A.50秒 B.45秒 C.40秒 D.35秒
8.广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表:若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短线路距离是( )
A.20.6 B.21 C.22 D.23
9.用:0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只使用一次),然后把所得的数相加,它们的和不可能是( )
A.36 B.117 C.115 D.153
10.甲,乙,丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲,乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
二.填空题(共5小题)
11.某班对思想品德、历史、地理三门课程的选考情况进行调研,数据如下:
科目 思想品德 历史 地理
选考人数(人) 20 13 18
其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有 人;该班至少有学生 人.
12.学校广播室要从八年级(2)班选一名广播员,小明、小华和小英普通话都不相上下,并且都争着要去.老师决定用抽签的办法确定,结果三个人都争着先抽,以为第一个抽签的人抽中的可能性大一些; 这时,小华从兜里拿出两枚一元的硬币,并说将两枚硬币同时向上抛出,如果两个都是正面朝上,小明去;如果两个都是反面朝上,小英去;如果两个一正一反,小华自己去.那么,你认为 (填“老师”或“小华”)的办法公平合理,理由是 .
13.绕湖的一周是24千米,小张和小王从湖边某一地点同时出发,反向而行,小王以每小时4千米速度每走60分钟后休息5分钟;小张以每小时6千米速度每走50分钟后休息10分钟,则两人出发后 分钟后第一次相遇.
14.重庆一中秉持“尊重自由、激发自觉”的教育理念,开展了丰富多彩的第二课堂及各种有趣有益的竞赛活动.其中“小棋王”争霸赛得到同学们的踊跃参与,经过初选、复试最后十位同学进入决赛这十位同学进行单循环比赛(每两人均赛一局),胜一局得2分、平局得1分、负一局得0分,最后按照每人的累计得分的多少进行排名,得分最高者就是第一名,以此类推.赛完后发现每人最后得分均不相同,第一名和第二名的同学均没负一局,他们两人的得分之和比第三名同学多20分,第四名同学的得分刚好是最后四名同学得分的总和,则第五名的同学得分为 分.
15.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块已确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 .(请填入方块上的字母)
三.解答题(共4小题)
16.某次数学竞赛中有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个是正确的.如表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 第二题 第三题 第四题 第五题 得分
甲 C C A B B 4
乙 C C B B C 3
丙 B C C B B 2
丁 B C C B A
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可)
17.甲、乙、丙三人中一个是教师,一个是护士.一个是工人.现在只知道丙比工人年龄大,甲和护士不同岁,护士比乙年龄小.请你猜猜他们当中谁是教师,并说明理由.
18.阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?
19.附加题:
要将29个数学竞赛的名额分配给10所学校,每所学校至少要分到一个名额.
(1)试提出一种分配方案,使得分到相同名额的学校少于4所;
(2)证明:不管怎样分配,至少有3所学校得到的名额相同;
(3)证明:如果分到相同名额的学校少于4所,则29名选手至少有5名来自同一学校.
试题解析
一.选择题(共10小题)
1.小明、小林和小颖共解出100道数学题,每人都解出了其中的60道,如果将其中只有1人解出的题叫做难题,2人解出的题叫做中档题,3人都解出的题叫做容易题,那么难题比容易题多多少道( )
A.15 B.20 C.25 D.30
解:设容易题有x道,中档题有y道,难题有z道,
由题意得,,
①×2﹣②得,z﹣x=20,
所以,难题比容易题多20道.
故选:B.
2.在一次1500米比赛中,有如下的判断:甲说:丙第一,我第三;乙说:我第一,丁第四;丙说:丁第二,
我第三.结果是每人的两句话中都只说对了一句,则可判断第一名是( )
A.甲 B.乙 C.丙 D.丁
解:根据分析,知
第一名应是乙.
故选:B.
3.某校七年级、八年级的学生人数相同,九年级的学生人数是八年级学生人数的,已知七年级的男生人数与八年级的女生人数相同,九年级男生人数占三个年级男生人数的,那么三个年级的男生与女生的比为( )
A. B. C. D.
解:设七年级总人数为x,则八年级总人数为x,九年级总人数为x;
设七年级男生人数为a,则女生人数为x﹣a;八年级女生人数为a,男生人数为x﹣a;
设九年级男生人数为b,则女生人数为x﹣b,
∵九年级男生人数占三个年级男生人数的,
∴三个年级男生人数为5b;=,
∴x=4b,
∵三个年级女生总人数为x﹣a+a+x﹣b=×4b﹣b=,
∴三个年级的男生与女生的比为5b:=,
故选:D.
4.为了传承中华文化,激发学生的爱国情怀,提高学生的文学素养,某学校初二(8)班举办了“乐知杯古诗词”大赛.现有小璟、小桦、小花三位同学进入了最后冠军的角逐.决赛共分为六轮,规定:每轮分别决出第1,2,3名(不并列),对应名次的得分都分别为a,b,c(a>b>c且a,b,c均为正整数);选手最后得分为各轮得分之和,得分最高者为冠军.如表是三位选手在每轮比赛中的部分得分情况,根据题中所给信息,下列说法正确的是( )
第一轮 第二轮 第三轮 第四轮 第五轮 第六轮 最后得分
小璟 a a 26
小桦 a b c 11
小花 b b 11
A.小璟可能有一轮比赛获得第二名
B.小桦有三轮比赛获得第三名
C.小花可能有一轮比赛获得第一名
D.每轮比赛第一名得分a为5
解:由题可知:(a+b+c)×6=26+11+11=48,其中a>b>c且a,b,c均为正整数.
∴a+b+c也是正整数,
∴a+b+c=8.
∵若每轮比赛第一名得分a为4,则最后得分最高为:4×6=24<26,
∴a>4,
∵又a>b>c,b+c最小取3,
∴4<a<6.
∴a=5,b=2,c=1,
∴每轮比赛第一名得分a为5,小璟5轮得第一,1轮得第三;小桦4轮得第三,1轮得第一,1轮得第二;小花5轮得第二,1轮得第三.
故选:D.
5.有一种“扫雷”游戏如图,方格内的数字表示与它相邻的方格内总共有的地雷数,例如:右下角的数字1表示A、B、C中只有一个地雷;通过推理,请判断?处应填的数字是.( )
2 3
3 A B
1 ? C 1
A.5 B.4 C.3 D.2
解:根据题意用是表示有地雷,用不表示没有地雷填表得:
是 是 2 3 是
3 不 是 不 是
1 是 ? 不 1
?的周围有两颗地雷,所以?处应填的数字是2.
故选:D.
6.某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
解:若甲对,即只参加一项的人数大于14人,不妨假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.
故选:B.
7.如图,汽车在东西向的公路l上行驶,途中A,B,C,D四个十字路口都有红绿灯.AB之间的距离为800米,BC为1000米,CD为1400米,且l上各路口的红绿灯设置为:同时亮红灯或同时亮绿灯,每次红(绿)灯亮的时间相同,红灯亮的时间与绿灯亮的时间也相同.若绿灯刚亮时,甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,这两辆汽车通过四个路口时都没有遇到红灯,则每次绿灯亮的时间可能设置为( )
A.50秒 B.45秒 C.40秒 D.35秒
解:∵甲汽车从A路口以每小时30千米的速度沿l向东行驶,同时乙汽车从D路口以相同的速度沿l向西行驶,
∴两车的速度为:=(m/s),
∵AB之间的距离为800米,BC为1000米,CD为1400米,
∴分别通过AB,BC,CD所用的时间为:=96(s),=120(s),=168(s),
∵这两辆汽车通过四个路口时都没有遇到红灯,
∴当每次绿灯亮的时间为50s时,∵=1,∴甲车到达B路口时遇到红灯,故A错误;
∴当每次绿灯亮的时间为45s时,∵=3,∴乙车到达C路口时遇到红灯,故B错误;
∴当每次绿灯亮的时间为40s时,∵=5,∴甲车到达C路口时遇到红灯,故C错误;
∴当每次绿灯亮的时间为35s时,∵=2,=6,=10,=4,=8,
∴这两辆汽车通过四个路口时都没有遇到红灯,故D正确;
则每次绿灯亮的时间可能设置为:35秒.
故选:D.
8.广州2010年亚运会火炬传递在A、B、C、D、E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表:若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短线路距离是( )
A.20.6 B.21 C.22 D.23
解:按路线ACBDE传递的距离为:4+7+6+5=22.
按路线ACDBE传递的距离为:4+9+6+2=21.
按路线ABCDE传递的距离为:5+7+9+5=26.
按路线ABDCE传递的距离为:5+6+9+8.6=28.6.
按路线ADCBE传递的距离为:5+9+7+2=23.
按路线ADBCE传递的距离为:5+6+7+8.6=26.6.
所以按路线ACDBE传递的距离最短,最短线路是21.
故选:B.
9.用:0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数(每个数字都只使用一次),然后把所得的数相加,它们的和不可能是( )
A.36 B.117 C.115 D.153
解:0+1+2+3+4+5+6+7+8=36,
2+3+4+5+6+17+80=117,
0+1+2+3+4+56+87=153,
故不能组成115.
故选:C.
10.甲,乙,丙三人进行乒乓球比赛,规则是:两人比赛,另一人当裁判,输者将在下一局中担任裁判,每一局比赛没有平局.已知甲,乙各比赛了4局,丙当了3次裁判.问第2局的输者是( )
A.甲 B.乙 C.丙 D.不能确定
解:由题意,知:三场比赛的对阵情况为:
第一场:甲VS乙,丙当裁判;
第二场:乙VS丙,甲当裁判;
第三场:甲VS乙,丙当裁判;
第四场:甲VS丙,乙当裁判;
第五场:乙VS甲,丙当裁判;
或第一场:甲VS乙,丙当裁判;
第二场:甲VS丙,乙当裁判;
第三场:甲VS乙,丙当裁判;
第四场:乙VS丙,甲当裁判;
第五场:乙VS甲,丙当裁判;
由于输球的人下局当裁判,因此第二场输的人是丙.
故选:C.
二.填空题(共5小题)
11.某班对思想品德、历史、地理三门课程的选考情况进行调研,数据如下:
科目 思想品德 历史 地理
选考人数(人) 20 13 18
其中思想品德、历史两门课程都选了的有3人,历史、地理两门课程都选了的有4人,则该班选了思想品德而没有选历史的有 17 人;该班至少有学生 30 人.
解:思想品德共有20人选择,其中选历史的有3人,所以选思想品德而没有选历史的有17人;
根据题意可以列表为:
所以该班选了思想品德而没有选历史的有17人;该班至少有学生30人.
故答案为:17,30.
12.学校广播室要从八年级(2)班选一名广播员,小明、小华和小英普通话都不相上下,并且都争着要去.老师决定用抽签的办法确定,结果三个人都争着先抽,以为第一个抽签的人抽中的可能性大一些; 这时,小华从兜里拿出两枚一元的硬币,并说将两枚硬币同时向上抛出,如果两个都是正面朝上,小明去;如果两个都是反面朝上,小英去;如果两个一正一反,小华自己去.那么,你认为 老师 (填“老师”或“小华”)的办法公平合理,理由是 老师的办法中,三人的机会相等,而小华的办法中,三人机会不等 .
解:老师,
因为老师的办法,不管谁先抽均有的机会;
而小华的办法中,有正反,正正,反正,反反4种情况,
小明和小英的机会各占,而小华的机会占=,
即老师的办法中,三人的机会相等,而小华的办法中,三人机会不等,
故答案为:老师;老师的办法中,三人的机会相等,而小华的办法中,三人机会不等.
13.绕湖的一周是24千米,小张和小王从湖边某一地点同时出发,反向而行,小王以每小时4千米速度每走60分钟后休息5分钟;小张以每小时6千米速度每走50分钟后休息10分钟,则两人出发后 160 分钟后第一次相遇.
解:∵小王65分行4千米,小张60分行6×=5千米,
∴小王130分行8千米,小张120分行10千米,
∴小张130分行10+×10=11千米;
∴在130分时间里,俩人一共行19千米,余下5千米还用5÷(+)=30分.所以出发160分第一次相遇.
故答案为160.
14.重庆一中秉持“尊重自由、激发自觉”的教育理念,开展了丰富多彩的第二课堂及各种有趣有益的竞赛活动.其中“小棋王”争霸赛得到同学们的踊跃参与,经过初选、复试最后十位同学进入决赛这十位同学进行单循环比赛(每两人均赛一局),胜一局得2分、平局得1分、负一局得0分,最后按照每人的累计得分的多少进行排名,得分最高者就是第一名,以此类推.赛完后发现每人最后得分均不相同,第一名和第二名的同学均没负一局,他们两人的得分之和比第三名同学多20分,第四名同学的得分刚好是最后四名同学得分的总和,则第五名的同学得分为 11 分.
解:因为每场比赛产生的最大分值是2分,这次比赛一共进行了45场比赛,因此产生的分值的最大值是90分.因为个人的最高得分是18分,又因为第一名选手与第二名选手均没有负一局,可以得出第一名选手与第二名选手是平一局,这个说明第一名选手最多17分,第二名选手最多16分,因此第一、二名选手的得分的和的最多33分.
情形1:当他们的总分是33分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分13分,.假设第四名选手得分12分,最后四名选手的得分总和为12分,由90﹣33﹣12﹣12=20可知,第5名为11分,第6名为9分.
情形2:当他们的总分是33分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分13分,假设第四名选手得分11分,最后四名选手的得分总和为11分,可知第5名与第6名的分数和为22分,两人中必有高于11分,与假设矛盾;
情形3:假设第一、二名选手的得分的和是32分时,因为第一、二名选手的得分的和比第三名选手的得分多20分,所以第三名选手的得分12分,.假设第四名选手得分11分,最后四名选手的得分总和为11分,可知第5名与第6名的分数和为24分,结果推出矛盾,
故第1名17分,第2名16分,第3名13分,第4名12分,第5名11分,第6名9分;
故答案为11
15.电脑系统中有个“扫雷”游戏,要求游戏者标出所有的雷,游戏规则:一个方块下面最多埋一个雷,如果无雷,掀开方块下面就标有数字,提醒游戏者此数字周围的方块(最多八个)中雷的个数(实际游戏中,0通常省略不标,为方便大家识别与印刷,我把图乙中的0都标出来了,以示与未掀开者的区别),如图甲中的“3”表示它的周围八个方块中仅有3个埋有雷.图乙是张三玩游戏中的局部,图中有4个方块已确定是雷(方块上标有旗子),则图乙第一行从左数起的七个方块中(方块上标有字母),能够确定一定是雷的有 B、D、F、G .(请填入方块上的字母)
解:图乙中最左边的“1”和最右边的“1”,可得如下推断
由第三行最左边的“1”,可得它的上方必定是雷.
结合B下方的“2”,可得最左边的A、B对应的方格中有一个雷;
同理可得最右边的“4”周围4个方格中有3个雷,中间D、E对应方格中有一个雷;
由于B下方的“2”和第二行最右边的“2”,它们周围的雷已经够数,
所以C对应的方格肯定不是雷,如下图所示:
进行下一步推理:
因为C对应的方格不是雷,所以C下方“2”的左上、右上的方格,即B、D都是雷;
而B下方的“2”的周围的雷也已经够数,所以A对应的方格也不是雷.
因为D下方的“2”,它的周围的雷已经够数,可得E对应的方格不是雷,
根据F下方的“4”周围应该有4个雷,结合E不是雷,可得F、G对应的方格都是雷.
综上所述,A、C、E对应的方格不是雷,且B、D、F、G对应的方格是雷.
故答案为:B、D、F、G.
三.解答题(共4小题)
16.某次数学竞赛中有5道选择题,每题1分,每道题在A、B、C三个选项中,只有一个是正确的.如表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 第二题 第三题 第四题 第五题 得分
甲 C C A B B 4
乙 C C B B C 3
丙 B C C B B 2
丁 B C C B A
(1)则甲同学错的是第 五 题;
(2)丁同学的得分是 3 ;
(3)如果有一个同学得了1分,他的答案可能是 CACCC (写出一种即可)
解:(1)∵有5道选择题,每题1分,
甲、乙、丙各得4,3,2分,
观察表格可知:第二题选C和第四题选B,甲、乙、丙、丁四位同学都正确,
所以丙同学答对第二题和第四题,得2分;
第一题选C,甲和乙同学都正确,
所以乙同学答对了第一、第二、第四题,得3分;
通过第三题可知:
乙,丙同学选B,C都答错了,
所以选项A正确,
所以第三题选A;
通过第五题,乙、丙两位同学选C和B都错误,
所以选A正确,
所以甲同学错的是第五题;
故答案为:五;
(2)因为五个题的正确答案是:C、C、A、B、A,
所以丁同学答对了第二、四、五题,
所以丁同学得分是3分.
故答案为:3;
(3)如果有一个同学得了1分,他的答案可能是:C、A、C、C、C(答案不唯一).
故答案为:C、A、C、C、C.
17.甲、乙、丙三人中一个是教师,一个是护士.一个是工人.现在只知道丙比工人年龄大,甲和护士不同岁,护士比乙年龄小.请你猜猜他们当中谁是教师,并说明理由.
解:乙是教师,
理由如下:∵甲和护士不同岁,护士比乙年龄小,
∴甲、乙都不是护士,
∴丙是护士,
∵护士比工人年龄大,护士比乙年龄小,
∴乙不是工人,
∴乙是教师.
18.阅读以下材料,并解答以下问题.
“完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.”如完成沿图1所示的街道从A点出发向B点行进这件事(规定必须向北走,或向东走),会有多种不同的走法,其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,将数字填入图2的空圆中,并回答从A点出发到B点的走法共有多少种?
(2)运用适当的原理和方法算出从A点出发到达B点,并禁止通过交叉点C的走法有多少种?
(3)现由于交叉点C道路施工,禁止通行.求如任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是多少?
解:(1)∵完成从A点到B点必须向北走,或向东走,
∴到达A点以外的任意交叉点的走法数只能是与其相邻的南边交叉点和西边交叉点的数字之和,
故使用分类加法计数原理,由此算出从A点到达其余各交叉点的走法数,填表如图1.
答:从A点到B点的走法共有35种.
(2)方法一:可先求从A点到B点,并经过交叉点C的走法数,再用从A点到B点总走法数减去它,即得从A点到B点,但不经过交叉点C的走法数.
完成从A点出发经C点到B点这件事可分两步,先从A点到C点,再从C点到B点,
使用分类加法计数原理,算出从A点到C点的走法是3种,见图2;算出从C点到B点的走法为6种,见图3,再运用分步乘法计数原理,得到从A点经C点到B点的走法有3×6=18种.
∴从A点到B点但不经过C点的走法数为35﹣18=17种.
方法二:由于交叉点C道路施工,禁止通行,故视为相邻道路不通,可删除与C点紧相连的线段,运用分类加法计数原理,算出从A点到B点并禁止通过交叉点C的走法有17种.从A点到各交叉点的走法数见图4,
∴从A点到B点并禁止经过C点的走法数为35﹣18=17种.
(3)P(顺利开车到达B点)=.
答:任选一种走法,顺利开车到达B点的概率是.
19.附加题:
要将29个数学竞赛的名额分配给10所学校,每所学校至少要分到一个名额.
(1)试提出一种分配方案,使得分到相同名额的学校少于4所;
(2)证明:不管怎样分配,至少有3所学校得到的名额相同;
(3)证明:如果分到相同名额的学校少于4所,则29名选手至少有5名来自同一学校.
解:(1)满足要求的分配方案有很多,如:学校对应的名额可以分别是:1,1,1,2,2,2,3,3,7,7;
(2)假设没有3所学校得到相同的名额,而每校至少要有1名,则人数最少的分配方案是:每两所学校一组依次各得1,2,3,4,5个名额,总人数为2(1+2+3+4+5)=30,但现在只有29个名额,故不管如何分配,都至少有3所学校分得的名额相同;
(3)假设每所学校分得的名额都不超过4,并且每校的名额不少于1,则在分到相同名额的学校少于4所的条件下,10所学校派出的选手数最多不会超过3×4+3×3+3×2+1×1=28,这与选手总数是29矛盾,从而至少有一所学校派出的选手数不小于5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
