【高频易错题汇编】1.6 完全平方公式(含解析)
文档属性
| 名称 | 【高频易错题汇编】1.6 完全平方公式(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 17:01:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
1.6 完全平方公式 高频易错题集
一.选择题(共10小题)
1.下列计算正确的是( )
A.(x2)3=x9 B.(﹣x)2?x=x3
C.(﹣2ab2)2=﹣4a2b4 D.(x﹣y)2=x2﹣y2
2.下列运算一定正确的是( )
A.a2+a2=a4 B.a2?a4=a8
C.(a2)4=a8 D.(a+b)2=a2+b2
3.下列计算正确的是( )
A.(﹣2a2)4=8a8 B.a3+a=a4
C.a5÷a2=a3 D.(a+b)2=a2+b2
4.下列计算正确的是( )
A.a2+b2=(a+b)2 B.a2+a4=a6
C.a10÷a5=a2 D.a2?a3=a5
5.如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
6.已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )
A.a2+2a+1 B.a2﹣2a+1 C.a2+1 D.a+1
7.把长和宽分别为a和b的四个相同的小长方形拼成如图的正方形,图形中阴影部分面积正好可以验证下面等式的正确性的是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
8.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图1可以得到(a+b)2=a2+2ab+b2,那么利用图2所得到的数学等式是( )
A.(a+b+c)2=a2+b2+c2
B.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
C.(a+b+c)2=a2+b2+b2+ab+ac+bc
D.(a+b+c)2=2a+2b+2c
9.如果x2+2mx+9是一个完全平方式,则m的值是( )
A.3 B.±3 C.6 D.±6
10.若4x2﹣kxy+9y2是完全平方式,则k的值是( )
A.±6 B.±12 C.±36 D.±72
二.填空题(共5小题)
11.已知:a+b=3,则代数式a2+2ab+b2的值为 .
12.计算:(a+2b)2= .
13.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
14.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
15.若x2+6x+m(m为常数)是一个完全平方式,则m的值是 .
三.解答题(共5小题)
16.若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
17.计算
(1)(π﹣2)0﹣3﹣2;
(2)(a﹣1)2+a(3﹣a).
18.“若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值”
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值
(2)若x满足(2015﹣x)2+(2013﹣x)2=4032,求(2015﹣x)(2013﹣x)的值
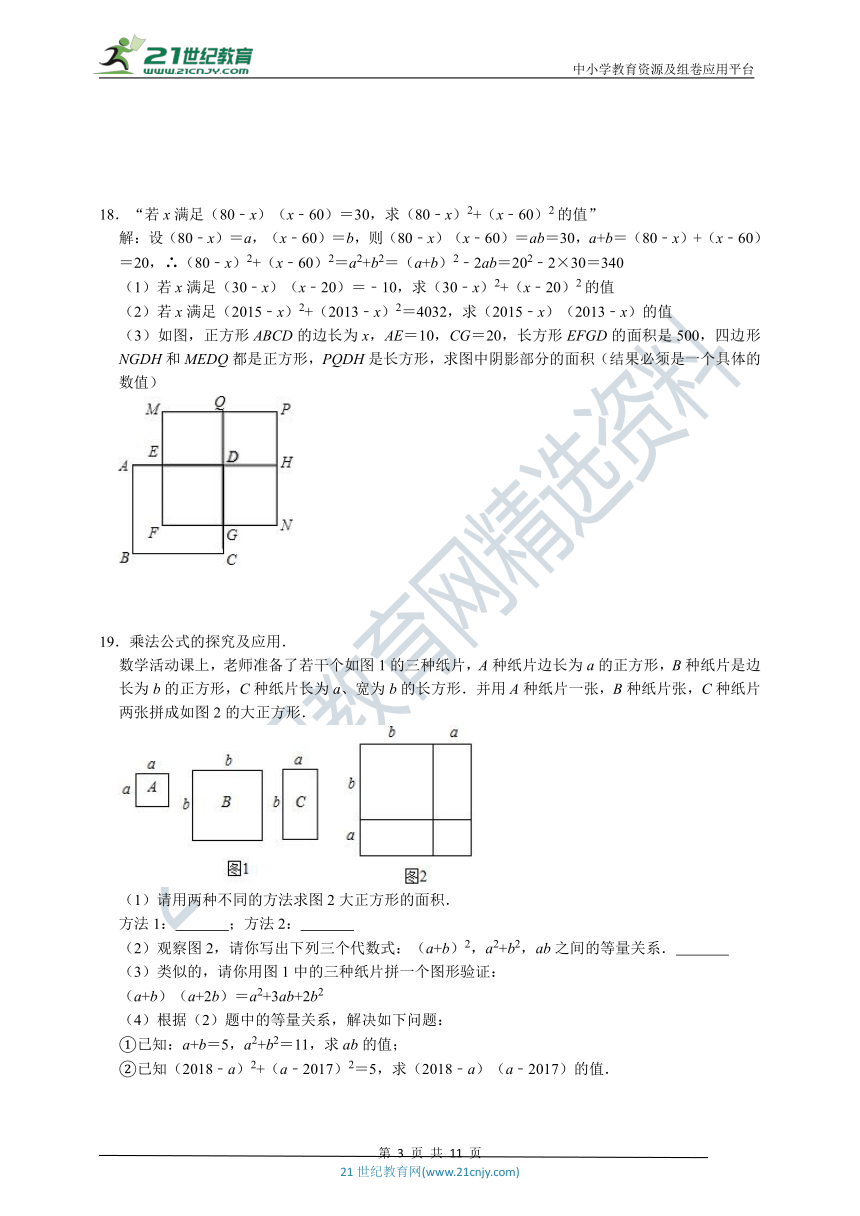
(3)如图,正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值)
19.乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
20.如果a2﹣2(k﹣1)ab+9b2是一个完全平方式,那么k= .
试题解析
一.选择题(共10小题)
1.下列计算正确的是( )
A.(x2)3=x9 B.(﹣x)2?x=x3
C.(﹣2ab2)2=﹣4a2b4 D.(x﹣y)2=x2﹣y2
解:A、(x2)3=x6,原计算错误,故此选项不符合题意;
B、(﹣x)2?x=x3,原计算正确,故此选项符合题意;
C、(﹣2ab2)2=4a2b4,原计算错误,故此选项不符合题意;
D、(x﹣y)2=x2﹣2xy+y2,原计算错误,故此选项不符合题意;
故选:B.
总结:此题主要考查了幂的乘方、同底数幂的乘法、积的乘方的运算法则,以及完全平方公式等知识,能够正确运用法则和公式是解题的关键.
2.下列运算一定正确的是( )
A.a2+a2=a4 B.a2?a4=a8
C.(a2)4=a8 D.(a+b)2=a2+b2
解:A、a2+a2=2a2,原计算错误,故此选项不合题意;
B、a2?a4=a6,原计算错误,故此选项不合题意;
C、(a2)4=a8,原计算正确,故此选项合题意;
D、(a+b)2=a2+2ab+b2,原计算错误,故此选项不合题意.
故选:C.
总结:本题主要考查了完全平方公式,同底数幂的乘法,幂的乘方以及合并同类项的法则,熟记公式和运算法则是解答本题的关键.
3.下列计算正确的是( )
A.(﹣2a2)4=8a8 B.a3+a=a4
C.a5÷a2=a3 D.(a+b)2=a2+b2
解:A.(﹣2a2)4=16a8,故本选项不合题意;
B.a3与a不是同类项,所以不能合并,故本选项不合题意;
C.a5÷a2=a3,正确;
D.(a+b)2=a2+2ab+b2,故本选项不合题意.
故选:C.
总结:本题主要考查了同底数幂的除法,完全平方公式,合并同类项以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.
4.下列计算正确的是( )
A.a2+b2=(a+b)2 B.a2+a4=a6
C.a10÷a5=a2 D.a2?a3=a5
解:A、a2+2ab+b2=(a+b)2,原计算错误,故此选项不符合题意;
B、a2与a4不是同类项不能合并,原计算错误,故此选项不符合题意;
C、a10÷a5=a5,原计算错误,故此选项不符合题意;
D、a2?a3=a5,原计算正确,故此选项符合题意;
故选:D.
总结:此题考查了整式的运算,熟练掌握运算法则是解本题的关键.
5.如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
解:∵大正方形的面积﹣小正方形的面积=4个矩形的面积,
∴(a+b)2﹣(a﹣b)2=4ab,即4ab=(a+b)2﹣(a﹣b)2.
故选:C.
总结:考查了完全平方公式的几何背景,能够正确找到大正方形和小正方形的边长是难点.解决问题的关键是读懂题意,找到所求的量的等量关系.
6.已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )
A.a2+2a+1 B.a2﹣2a+1 C.a2+1 D.a+1
解:新正方形的边长为a+1,
∴新正方形的面积为(a+1)2=a2+2a+1,
故选:A.
总结:本题主要考查了完全平方公式的运用,解决问题的关键是掌握完全平方公式.
7.把长和宽分别为a和b的四个相同的小长方形拼成如图的正方形,图形中阴影部分面积正好可以验证下面等式的正确性的是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
解:阴影部分的面积是:(a+b)2﹣(a﹣b)2;
4个长方形的面积是:4ab,
∴验证的等式是:(a+b)2﹣(a﹣b)2=4ab.
故选:D.
总结:本题考查对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.
8.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图1可以得到(a+b)2=a2+2ab+b2,那么利用图2所得到的数学等式是( )
A.(a+b+c)2=a2+b2+c2
B.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
C.(a+b+c)2=a2+b2+b2+ab+ac+bc
D.(a+b+c)2=2a+2b+2c
解:∵正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故选:B.
总结:本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.
9.如果x2+2mx+9是一个完全平方式,则m的值是( )
A.3 B.±3 C.6 D.±6
解:∵x2+2mx+9是一个完全平方式,
∴2m=±6,
∴m=±3,
故选:B.
总结:本题考查了完全平方公式,完全平方公式是两数的平方和加减积的2倍,注意符合条件的m值有两个.
10.若4x2﹣kxy+9y2是完全平方式,则k的值是( )
A.±6 B.±12 C.±36 D.±72
解:∵4x2﹣kxy+9y2是完全平方式,
∴﹣kxy=±2×2x?3y,
解得k=±12.
故选:B.
总结:本题主要考查完全平方式,解决问题的关键是根据两平方项确定出这两个数,再根据乘积二倍项求解.
二.填空题(共5小题)
11.已知:a+b=3,则代数式a2+2ab+b2的值为 9 .
解:因为a+b=3,
所以a2+2ab+b2=(a+b)2=32=9.
故答案为:9.
总结:本题考查了完全平分公式,解决本题的关键是熟记完全平分公式.
12.计算:(a+2b)2= a2+4ab+4b2 .
解:原式=a2+4ab+4b2
=a2+4ab+4b2,
故答案为:a2+4ab+4b2.
总结:本题考查了完全平方公式的运用,熟练运用公式是解题的关键,注意:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2.
13.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 20 .
解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)
=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)
=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
总结:此题考查整式的混合运算,关键是利用面积的和差关系求出四边形的面积,但在计算时要把未知的代数式转化成已知,代入求值.
14.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 18 .
解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
总结:本题综合考查了完全平方公式几何背景的应用,正方形的面积公式,列二元二次方程组等知识,重点掌握完全平方公式几何背景应用,难点是巧用二元二次方程求解两个正方形的面积和.
15.若x2+6x+m(m为常数)是一个完全平方式,则m的值是 9 .
解:∵x2+6x+m(m为常数)是一个完全平方式,
∴m=32=9,
故答案为:9.
总结:此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
三.解答题(共5小题)
16.若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
解:(1)∵(x+3)(y+3)=12,
∴xy+3x+3y+9=12,
则xy+3(x+y)=3,
将x+y=2代入得xy+6=3,
则xy=﹣3;
(2)当xy=﹣3、x+y=2时,
原式=(x+y)2+xy
=22+(﹣3)
=4﹣3
=1.
总结:本题主要考查多项式乘多项式,解题的关键是掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.
17.计算
(1)(π﹣2)0﹣3﹣2;
(2)(a﹣1)2+a(3﹣a).
解:(1)(π﹣2)0﹣3﹣2
=1﹣
=;
(2)(a﹣1)2+a(3﹣a)
=a2﹣2a+1+3a﹣a2
=a+1.
总结:本题考查了实数的运算和整式的运算.解题的关键是掌握实数的运算的法则和整式的运算的法则.
18.“若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值”
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值
(2)若x满足(2015﹣x)2+(2013﹣x)2=4032,求(2015﹣x)(2013﹣x)的值
(3)如图,正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值)
解:(1)设(30﹣x)=m,(x﹣20)=n,
则(30﹣x)(x﹣20)=mn=﹣10,m+n=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=m2+n2=(m+n)2﹣2mn=(﹣10)2﹣2×(﹣10)=120;
(2)设(2015﹣x)=c,(2013﹣x)=d,
则(2015﹣x)2+(2013﹣x)2=c2+d2=4032,c﹣d=(2015﹣x)﹣(2013﹣x)=2,
2cd=(c2+d2)﹣(c﹣d)2=4032﹣22=4028,
cd=2014,
∴(2015﹣x)(2013﹣x)=cd=2014.
(3)∵正方形ABCD的边长为x,AE=10,CG=20,
∴DE=(x﹣10),DG=x﹣20,
∴(x﹣10)(x﹣20)=500,
设(x﹣10)=a,(x﹣20)=b,
∴ab=500,a﹣b=(x﹣10)﹣(x﹣20)=10,
∴a2+b2=(a﹣b)2+2ab=102+2×500=1100,
∴阴影部分的面积为:a2+b2+2ab=1100+2×500=2100.
总结:本题考查了完全平分公式,解决本题的关键是熟记完全平分公式,进行转化运用.
19.乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1: (a+b)2 ;方法2: a2+b2+2ab
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系. (a+b)2=a2+2ab+b2
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
解:(1)图2大正方形的面积=(a+b)2
图2大正方形的面积=a2+b2+2ab
故答案为:(a+b)2,a2+b2+2ab;
(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2
故答案为:(a+b)2=a2+2ab+b2;
(3)如图所示,
(4)①∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7;
②设2018﹣a=x,a﹣2017=y,则x+y=1,
∵(2018﹣a)2+(a﹣2017)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy==﹣2,
即(2018﹣a)(a﹣2017)=﹣2.
20.如果a2﹣2(k﹣1)ab+9b2是一个完全平方式,那么k= 4或﹣2 .
解:∵a2﹣2(k﹣1)ab+9b2=a2﹣2(k﹣1)ab+(3b)2,
∴﹣2(k﹣1)ab=±2×a×3b,
∴k﹣1=3或k﹣1=﹣3,
解得k=4或k=﹣2.
即k=4或﹣2.
故答案为:4或﹣2.
_21?????????è?????(www.21cnjy.com)_
1.6 完全平方公式 高频易错题集
一.选择题(共10小题)
1.下列计算正确的是( )
A.(x2)3=x9 B.(﹣x)2?x=x3
C.(﹣2ab2)2=﹣4a2b4 D.(x﹣y)2=x2﹣y2
2.下列运算一定正确的是( )
A.a2+a2=a4 B.a2?a4=a8
C.(a2)4=a8 D.(a+b)2=a2+b2
3.下列计算正确的是( )
A.(﹣2a2)4=8a8 B.a3+a=a4
C.a5÷a2=a3 D.(a+b)2=a2+b2
4.下列计算正确的是( )
A.a2+b2=(a+b)2 B.a2+a4=a6
C.a10÷a5=a2 D.a2?a3=a5
5.如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
6.已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )
A.a2+2a+1 B.a2﹣2a+1 C.a2+1 D.a+1
7.把长和宽分别为a和b的四个相同的小长方形拼成如图的正方形,图形中阴影部分面积正好可以验证下面等式的正确性的是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
8.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图1可以得到(a+b)2=a2+2ab+b2,那么利用图2所得到的数学等式是( )
A.(a+b+c)2=a2+b2+c2
B.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
C.(a+b+c)2=a2+b2+b2+ab+ac+bc
D.(a+b+c)2=2a+2b+2c
9.如果x2+2mx+9是一个完全平方式,则m的值是( )
A.3 B.±3 C.6 D.±6
10.若4x2﹣kxy+9y2是完全平方式,则k的值是( )
A.±6 B.±12 C.±36 D.±72
二.填空题(共5小题)
11.已知:a+b=3,则代数式a2+2ab+b2的值为 .
12.计算:(a+2b)2= .
13.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 .
14.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
15.若x2+6x+m(m为常数)是一个完全平方式,则m的值是 .
三.解答题(共5小题)
16.若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
17.计算
(1)(π﹣2)0﹣3﹣2;
(2)(a﹣1)2+a(3﹣a).
18.“若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值”
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值
(2)若x满足(2015﹣x)2+(2013﹣x)2=4032,求(2015﹣x)(2013﹣x)的值
(3)如图,正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值)
19.乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
20.如果a2﹣2(k﹣1)ab+9b2是一个完全平方式,那么k= .
试题解析
一.选择题(共10小题)
1.下列计算正确的是( )
A.(x2)3=x9 B.(﹣x)2?x=x3
C.(﹣2ab2)2=﹣4a2b4 D.(x﹣y)2=x2﹣y2
解:A、(x2)3=x6,原计算错误,故此选项不符合题意;
B、(﹣x)2?x=x3,原计算正确,故此选项符合题意;
C、(﹣2ab2)2=4a2b4,原计算错误,故此选项不符合题意;
D、(x﹣y)2=x2﹣2xy+y2,原计算错误,故此选项不符合题意;
故选:B.
总结:此题主要考查了幂的乘方、同底数幂的乘法、积的乘方的运算法则,以及完全平方公式等知识,能够正确运用法则和公式是解题的关键.
2.下列运算一定正确的是( )
A.a2+a2=a4 B.a2?a4=a8
C.(a2)4=a8 D.(a+b)2=a2+b2
解:A、a2+a2=2a2,原计算错误,故此选项不合题意;
B、a2?a4=a6,原计算错误,故此选项不合题意;
C、(a2)4=a8,原计算正确,故此选项合题意;
D、(a+b)2=a2+2ab+b2,原计算错误,故此选项不合题意.
故选:C.
总结:本题主要考查了完全平方公式,同底数幂的乘法,幂的乘方以及合并同类项的法则,熟记公式和运算法则是解答本题的关键.
3.下列计算正确的是( )
A.(﹣2a2)4=8a8 B.a3+a=a4
C.a5÷a2=a3 D.(a+b)2=a2+b2
解:A.(﹣2a2)4=16a8,故本选项不合题意;
B.a3与a不是同类项,所以不能合并,故本选项不合题意;
C.a5÷a2=a3,正确;
D.(a+b)2=a2+2ab+b2,故本选项不合题意.
故选:C.
总结:本题主要考查了同底数幂的除法,完全平方公式,合并同类项以及幂的乘方与积的乘方,熟记幂的运算法则是解答本题的关键.
4.下列计算正确的是( )
A.a2+b2=(a+b)2 B.a2+a4=a6
C.a10÷a5=a2 D.a2?a3=a5
解:A、a2+2ab+b2=(a+b)2,原计算错误,故此选项不符合题意;
B、a2与a4不是同类项不能合并,原计算错误,故此选项不符合题意;
C、a10÷a5=a5,原计算错误,故此选项不符合题意;
D、a2?a3=a5,原计算正确,故此选项符合题意;
故选:D.
总结:此题考查了整式的运算,熟练掌握运算法则是解本题的关键.
5.如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写出一个代数恒等式是( )
A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
解:∵大正方形的面积﹣小正方形的面积=4个矩形的面积,
∴(a+b)2﹣(a﹣b)2=4ab,即4ab=(a+b)2﹣(a﹣b)2.
故选:C.
总结:考查了完全平方公式的几何背景,能够正确找到大正方形和小正方形的边长是难点.解决问题的关键是读懂题意,找到所求的量的等量关系.
6.已知一个正方形的边长为a,将该正方形的边长增加1,则得到的新正方形的面积为( )
A.a2+2a+1 B.a2﹣2a+1 C.a2+1 D.a+1
解:新正方形的边长为a+1,
∴新正方形的面积为(a+1)2=a2+2a+1,
故选:A.
总结:本题主要考查了完全平方公式的运用,解决问题的关键是掌握完全平方公式.
7.把长和宽分别为a和b的四个相同的小长方形拼成如图的正方形,图形中阴影部分面积正好可以验证下面等式的正确性的是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
解:阴影部分的面积是:(a+b)2﹣(a﹣b)2;
4个长方形的面积是:4ab,
∴验证的等式是:(a+b)2﹣(a﹣b)2=4ab.
故选:D.
总结:本题考查对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形面积展开分析.
8.对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如利用图1可以得到(a+b)2=a2+2ab+b2,那么利用图2所得到的数学等式是( )
A.(a+b+c)2=a2+b2+c2
B.(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
C.(a+b+c)2=a2+b2+b2+ab+ac+bc
D.(a+b+c)2=2a+2b+2c
解:∵正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故选:B.
总结:本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.
9.如果x2+2mx+9是一个完全平方式,则m的值是( )
A.3 B.±3 C.6 D.±6
解:∵x2+2mx+9是一个完全平方式,
∴2m=±6,
∴m=±3,
故选:B.
总结:本题考查了完全平方公式,完全平方公式是两数的平方和加减积的2倍,注意符合条件的m值有两个.
10.若4x2﹣kxy+9y2是完全平方式,则k的值是( )
A.±6 B.±12 C.±36 D.±72
解:∵4x2﹣kxy+9y2是完全平方式,
∴﹣kxy=±2×2x?3y,
解得k=±12.
故选:B.
总结:本题主要考查完全平方式,解决问题的关键是根据两平方项确定出这两个数,再根据乘积二倍项求解.
二.填空题(共5小题)
11.已知:a+b=3,则代数式a2+2ab+b2的值为 9 .
解:因为a+b=3,
所以a2+2ab+b2=(a+b)2=32=9.
故答案为:9.
总结:本题考查了完全平分公式,解决本题的关键是熟记完全平分公式.
12.计算:(a+2b)2= a2+4ab+4b2 .
解:原式=a2+4ab+4b2
=a2+4ab+4b2,
故答案为:a2+4ab+4b2.
总结:本题考查了完全平方公式的运用,熟练运用公式是解题的关键,注意:(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2.
13.如图,两个正方形的边长分别为a,b,若a+b=10,ab=20,则四边形ABCD的面积为 20 .
解:根据题意可得,四边形ABCD的面积
=(a2+b2)﹣﹣b(a+b)
=(a2+b2﹣ab)
=(a2+b2+2ab﹣3ab)
=[(a+b)2﹣3ab];
代入a+b=10,ab=20,可得:
四边形ABCD的面积=(10×10﹣20×3)÷2=20.
故答案为:20.
总结:此题考查整式的混合运算,关键是利用面积的和差关系求出四边形的面积,但在计算时要把未知的代数式转化成已知,代入求值.
14.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 18 .
解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
总结:本题综合考查了完全平方公式几何背景的应用,正方形的面积公式,列二元二次方程组等知识,重点掌握完全平方公式几何背景应用,难点是巧用二元二次方程求解两个正方形的面积和.
15.若x2+6x+m(m为常数)是一个完全平方式,则m的值是 9 .
解:∵x2+6x+m(m为常数)是一个完全平方式,
∴m=32=9,
故答案为:9.
总结:此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.
三.解答题(共5小题)
16.若x+y=2,且(x+3)(y+3)=12.
(1)求xy的值;
(2)求x2+3xy+y2的值.
解:(1)∵(x+3)(y+3)=12,
∴xy+3x+3y+9=12,
则xy+3(x+y)=3,
将x+y=2代入得xy+6=3,
则xy=﹣3;
(2)当xy=﹣3、x+y=2时,
原式=(x+y)2+xy
=22+(﹣3)
=4﹣3
=1.
总结:本题主要考查多项式乘多项式,解题的关键是掌握多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.
17.计算
(1)(π﹣2)0﹣3﹣2;
(2)(a﹣1)2+a(3﹣a).
解:(1)(π﹣2)0﹣3﹣2
=1﹣
=;
(2)(a﹣1)2+a(3﹣a)
=a2﹣2a+1+3a﹣a2
=a+1.
总结:本题考查了实数的运算和整式的运算.解题的关键是掌握实数的运算的法则和整式的运算的法则.
18.“若x满足(80﹣x)(x﹣60)=30,求(80﹣x)2+(x﹣60)2的值”
解:设(80﹣x)=a,(x﹣60)=b,则(80﹣x)(x﹣60)=ab=30,a+b=(80﹣x)+(x﹣60)=20,∴(80﹣x)2+(x﹣60)2=a2+b2=(a+b)2﹣2ab=202﹣2×30=340
(1)若x满足(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值
(2)若x满足(2015﹣x)2+(2013﹣x)2=4032,求(2015﹣x)(2013﹣x)的值
(3)如图,正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积是500,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体的数值)
解:(1)设(30﹣x)=m,(x﹣20)=n,
则(30﹣x)(x﹣20)=mn=﹣10,m+n=(30﹣x)+(x﹣20)=10,
∴(30﹣x)2+(x﹣20)2=m2+n2=(m+n)2﹣2mn=(﹣10)2﹣2×(﹣10)=120;
(2)设(2015﹣x)=c,(2013﹣x)=d,
则(2015﹣x)2+(2013﹣x)2=c2+d2=4032,c﹣d=(2015﹣x)﹣(2013﹣x)=2,
2cd=(c2+d2)﹣(c﹣d)2=4032﹣22=4028,
cd=2014,
∴(2015﹣x)(2013﹣x)=cd=2014.
(3)∵正方形ABCD的边长为x,AE=10,CG=20,
∴DE=(x﹣10),DG=x﹣20,
∴(x﹣10)(x﹣20)=500,
设(x﹣10)=a,(x﹣20)=b,
∴ab=500,a﹣b=(x﹣10)﹣(x﹣20)=10,
∴a2+b2=(a﹣b)2+2ab=102+2×500=1100,
∴阴影部分的面积为:a2+b2+2ab=1100+2×500=2100.
总结:本题考查了完全平分公式,解决本题的关键是熟记完全平分公式,进行转化运用.
19.乘法公式的探究及应用.
数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积.
方法1: (a+b)2 ;方法2: a2+b2+2ab
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系. (a+b)2=a2+2ab+b2
(3)类似的,请你用图1中的三种纸片拼一个图形验证:
(a+b)(a+2b)=a2+3ab+2b2
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
解:(1)图2大正方形的面积=(a+b)2
图2大正方形的面积=a2+b2+2ab
故答案为:(a+b)2,a2+b2+2ab;
(2)由题可得(a+b)2,a2+b2,ab之间的等量关系为:(a+b)2=a2+2ab+b2
故答案为:(a+b)2=a2+2ab+b2;
(3)如图所示,
(4)①∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7;
②设2018﹣a=x,a﹣2017=y,则x+y=1,
∵(2018﹣a)2+(a﹣2017)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy==﹣2,
即(2018﹣a)(a﹣2017)=﹣2.
20.如果a2﹣2(k﹣1)ab+9b2是一个完全平方式,那么k= 4或﹣2 .
解:∵a2﹣2(k﹣1)ab+9b2=a2﹣2(k﹣1)ab+(3b)2,
∴﹣2(k﹣1)ab=±2×a×3b,
∴k﹣1=3或k﹣1=﹣3,
解得k=4或k=﹣2.
即k=4或﹣2.
故答案为:4或﹣2.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
