第五章 第四节圆周运动 课件(共41张PPT)
文档属性
| 名称 | 第五章 第四节圆周运动 课件(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 767.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-06 17:21:07 | ||
图片预览







文档简介
(共41张PPT)
第四节
圆周运动
判断以下说法是否正确
做圆周运动的物体受到的合外力等于向心力.
向心力总是在圆周平面内并指向圆心,是恒力.
光滑桌面上手拉小球做匀速圆周运动,小球受到重力,支持力,拉力和向心力四个作用.
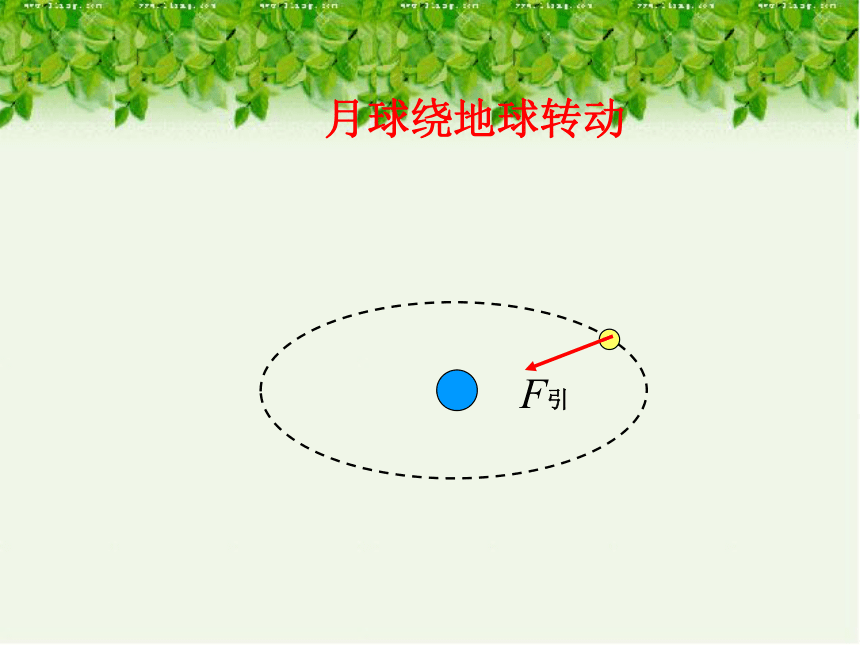
月球绕地球转动
F引
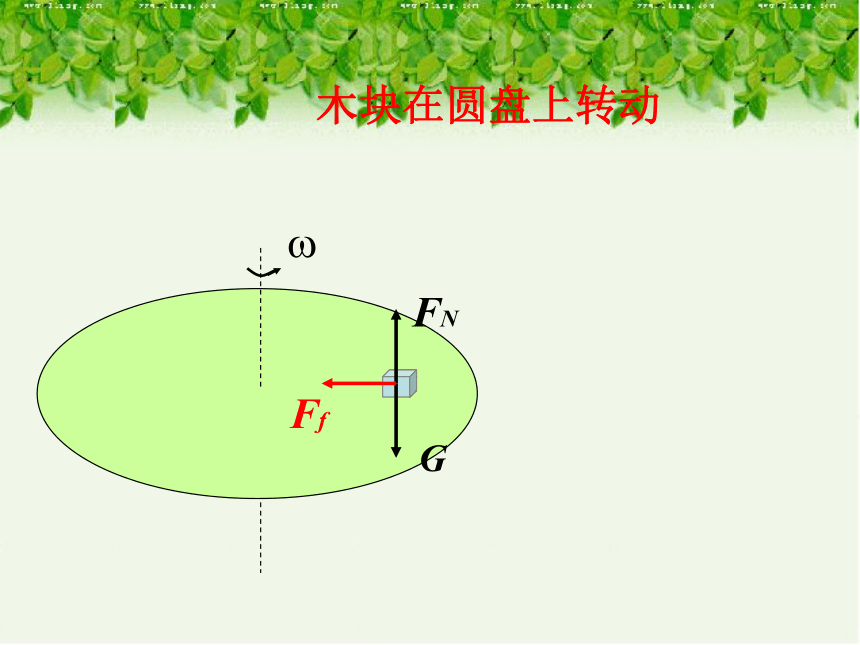
木块在圆盘上转动
G
FN
Ff
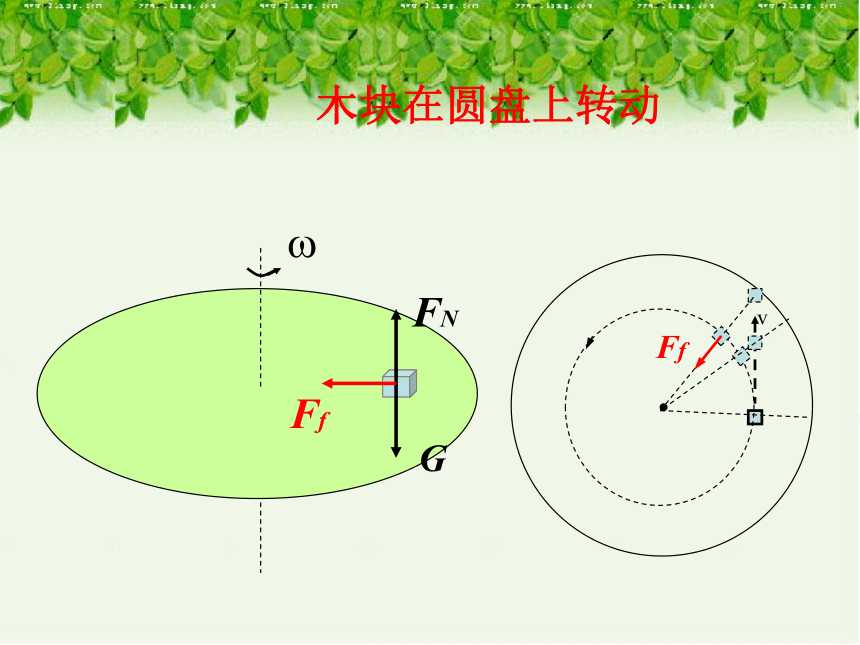
木块在圆盘上转动
G
FN
Ff
v
Ff
(一)水平面内的圆周运动
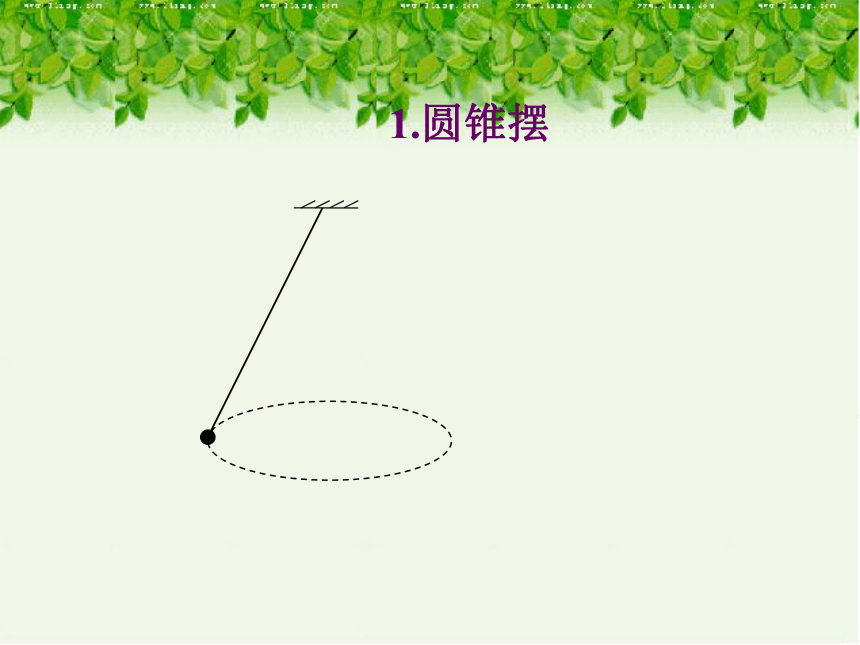
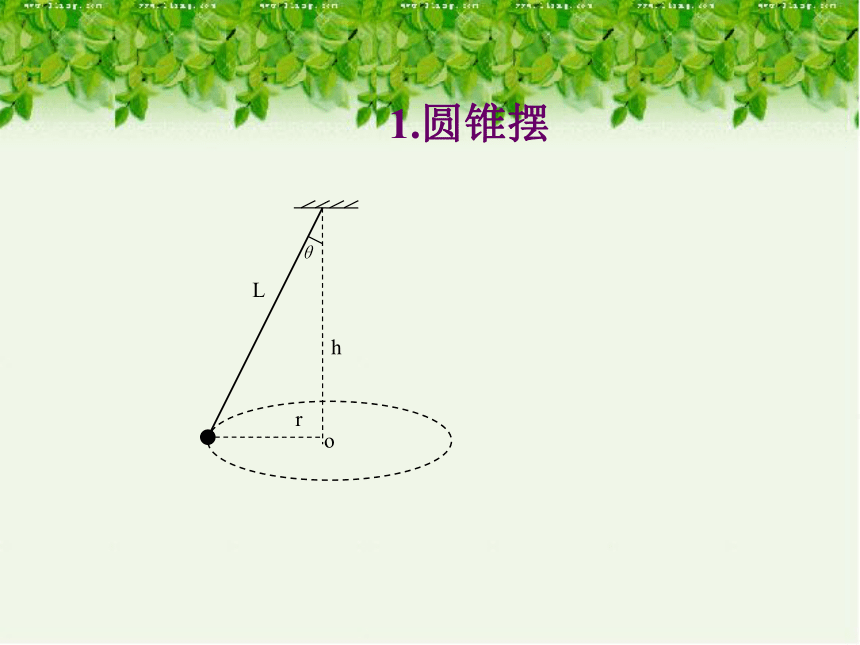
1.圆锥摆
1.圆锥摆
L
r
h
θ
o
1.圆锥摆
L
r
h
θ
G
FT
F向
θ
o
1.圆锥摆
L
r
h
θ
G
FT
F向
θ
o
ω越大,cosθ
越小,则θ越大。
θ≠0,若θ=0,则不为圆锥摆;
θ≠90°,若θ=90°则ω=∞,不可能。
1.圆锥摆
FT与小球质量m,摆长l以及角速度ω有关。FT >mg,小球处于超重状态。
L
r
h
θ
FT
F向
θ
o
处理圆周运动的
一般步骤
1、确定做圆周运动的物体为研究对象。(必要时将某一物从转动系统中隔离出来)
2、确定物体运动轨道的平面和圆心位置,以便确定向心力的方向;
3、分析物体的受力,明确向心力的来源。
4、圆周运动的动力学方程列方程求解。
2.火车转弯
2.火车转弯
2.火车转弯(水平轨道右转弯)
θ
2.火车转弯(倾斜轨道右转弯)
G
2FN
F合
θ
FN
FN
1.选择合适的θ,使向心力仅由FN和mg的合力F合提供,轮缘与轨道无挤压:
F向=F合
θ
2.当v〉v0
,F向〉F合
外轨道对外侧车轮轮缘有弹力
F外
G
2FN
F合
θ
FN
FN
1.选择合适的θ,使向心力仅由FN和mg的合力F合提供,轮缘与轨道无挤压:
F向=F合
θ
2.当v〉v0
,F向〉F合
外轨道对外侧车轮轮缘有弹力
3.当v〈v0
,F向〈F合
内轨道对内侧车轮轮缘有弹力
F内
铁路转弯处的圆弧半径是600m,轨距是1435mm,规定火车通过这里的速度是54km/h,内外轨的高度差应该是多大,才能使外轨刚好不受轮缘的挤压?
例题:
2.火车转弯
当θ很小时
G
2FN
F合
θ
θ
2.火车转弯(水平轨道右转弯)
h
L
轨道半径/
m
内外轨高度差/mm
50
330
100
200
150
165
200
132
250
110
300
火车弯道参数
火车转弯
拓 展:
1.解释高速公路的超车道比主车道更加倾斜。
2.自行车赛道比高速公路弯道更加倾斜
高速公路弯道行驶五注意
自行车赛道
高速公路弯道行驶五注意
???
1.转动方向盘不要过急。
???
2.尽可能不要踩刹车,这样会产生侧滑。
???
3.尽可能不要超车。
???
4.合理装载货物,不能超高,不能装偏,货物要摆放平稳,捆扎牢固。
???
5.转弯处如设有限速交通标志,绝不能超过规定的时速,否则会发生侧滑和翻车。
自行车赛道
处理圆周运动的
一般步骤
1、确定做圆周运动的物体为研究对象。(必要时将某一物从转动系统中隔离出来.)
2、确定物体运动轨道的平面和圆心位置,以便确定向心力的方向;
3、分析物体的受力明确向心力的来源。
4、圆周运动的动力学方程列方程求解。
思考题:
1.自行车转弯,稍一倾斜
就过去了,摩托车转弯倾斜度要大一些。摩托赛车时转弯,倾斜度更大,几乎倒在地上。
提问:谁提供向心力?倾斜度与向心力有关吗?有何关系?
思考题:
在圆圆的大厅里,杨利伟和战友们要坐在一只8米多长的铁臂夹着的圆筒里,在时速100公里高速旋转中,杨利伟和战友们要承受大约多大的压力?
(二)竖直面内的圆周运动
1.汽车过桥
G
FN
v
拱桥最高点
重力mg全部用以提供向心力,汽车恰好可以做圆周运动,汽车与桥的相互用力恰好等于0。
G
v
1.汽车过桥
拱桥最高点
1.汽车过桥
G
FN
v
拱桥最高点
汽车与桥之间有压力
此时,速度越小,支持力FN
越大;当v=0时,FN=0,汽车刚好不能过桥。
1.汽车过桥
G
v
拱桥最高点
重力不足以提供向心力,汽车做平抛运动。
1.汽车过桥
凹形桥最低点
FN
v
G
F向=F合
当v=0时,FN=mg汽车刚好不能过桥,当v>0且速度增大时,桥对车的支持力增大,
2.杂技节目“水流星”
FN
v
G
(V减小
,N
减小)
受力分析:
(V减小
,N
减小)
1.
重力恰好满足向心力的需求,水刚好能通过最高点。
2.
重力不能满足向心力的需求,由弹力来弥补,水也能通过最高点。
3.
水不能通过最高点,实际上小桶还没有到达最高点时已经离开圆周轨道做抛体运动了.。
第四节
圆周运动
判断以下说法是否正确
做圆周运动的物体受到的合外力等于向心力.
向心力总是在圆周平面内并指向圆心,是恒力.
光滑桌面上手拉小球做匀速圆周运动,小球受到重力,支持力,拉力和向心力四个作用.
月球绕地球转动
F引
木块在圆盘上转动
G
FN
Ff
木块在圆盘上转动
G
FN
Ff
v
Ff
(一)水平面内的圆周运动
1.圆锥摆
1.圆锥摆
L
r
h
θ
o
1.圆锥摆
L
r
h
θ
G
FT
F向
θ
o
1.圆锥摆
L
r
h
θ
G
FT
F向
θ
o
ω越大,cosθ
越小,则θ越大。
θ≠0,若θ=0,则不为圆锥摆;
θ≠90°,若θ=90°则ω=∞,不可能。
1.圆锥摆
FT与小球质量m,摆长l以及角速度ω有关。FT >mg,小球处于超重状态。
L
r
h
θ
FT
F向
θ
o
处理圆周运动的
一般步骤
1、确定做圆周运动的物体为研究对象。(必要时将某一物从转动系统中隔离出来)
2、确定物体运动轨道的平面和圆心位置,以便确定向心力的方向;
3、分析物体的受力,明确向心力的来源。
4、圆周运动的动力学方程列方程求解。
2.火车转弯
2.火车转弯
2.火车转弯(水平轨道右转弯)
θ
2.火车转弯(倾斜轨道右转弯)
G
2FN
F合
θ
FN
FN
1.选择合适的θ,使向心力仅由FN和mg的合力F合提供,轮缘与轨道无挤压:
F向=F合
θ
2.当v〉v0
,F向〉F合
外轨道对外侧车轮轮缘有弹力
F外
G
2FN
F合
θ
FN
FN
1.选择合适的θ,使向心力仅由FN和mg的合力F合提供,轮缘与轨道无挤压:
F向=F合
θ
2.当v〉v0
,F向〉F合
外轨道对外侧车轮轮缘有弹力
3.当v〈v0
,F向〈F合
内轨道对内侧车轮轮缘有弹力
F内
铁路转弯处的圆弧半径是600m,轨距是1435mm,规定火车通过这里的速度是54km/h,内外轨的高度差应该是多大,才能使外轨刚好不受轮缘的挤压?
例题:
2.火车转弯
当θ很小时
G
2FN
F合
θ
θ
2.火车转弯(水平轨道右转弯)
h
L
轨道半径/
m
内外轨高度差/mm
50
330
100
200
150
165
200
132
250
110
300
火车弯道参数
火车转弯
拓 展:
1.解释高速公路的超车道比主车道更加倾斜。
2.自行车赛道比高速公路弯道更加倾斜
高速公路弯道行驶五注意
自行车赛道
高速公路弯道行驶五注意
???
1.转动方向盘不要过急。
???
2.尽可能不要踩刹车,这样会产生侧滑。
???
3.尽可能不要超车。
???
4.合理装载货物,不能超高,不能装偏,货物要摆放平稳,捆扎牢固。
???
5.转弯处如设有限速交通标志,绝不能超过规定的时速,否则会发生侧滑和翻车。
自行车赛道
处理圆周运动的
一般步骤
1、确定做圆周运动的物体为研究对象。(必要时将某一物从转动系统中隔离出来.)
2、确定物体运动轨道的平面和圆心位置,以便确定向心力的方向;
3、分析物体的受力明确向心力的来源。
4、圆周运动的动力学方程列方程求解。
思考题:
1.自行车转弯,稍一倾斜
就过去了,摩托车转弯倾斜度要大一些。摩托赛车时转弯,倾斜度更大,几乎倒在地上。
提问:谁提供向心力?倾斜度与向心力有关吗?有何关系?
思考题:
在圆圆的大厅里,杨利伟和战友们要坐在一只8米多长的铁臂夹着的圆筒里,在时速100公里高速旋转中,杨利伟和战友们要承受大约多大的压力?
(二)竖直面内的圆周运动
1.汽车过桥
G
FN
v
拱桥最高点
重力mg全部用以提供向心力,汽车恰好可以做圆周运动,汽车与桥的相互用力恰好等于0。
G
v
1.汽车过桥
拱桥最高点
1.汽车过桥
G
FN
v
拱桥最高点
汽车与桥之间有压力
此时,速度越小,支持力FN
越大;当v=0时,FN=0,汽车刚好不能过桥。
1.汽车过桥
G
v
拱桥最高点
重力不足以提供向心力,汽车做平抛运动。
1.汽车过桥
凹形桥最低点
FN
v
G
F向=F合
当v=0时,FN=mg汽车刚好不能过桥,当v>0且速度增大时,桥对车的支持力增大,
2.杂技节目“水流星”
FN
v
G
(V减小
,N
减小)
受力分析:
(V减小
,N
减小)
1.
重力恰好满足向心力的需求,水刚好能通过最高点。
2.
重力不能满足向心力的需求,由弹力来弥补,水也能通过最高点。
3.
水不能通过最高点,实际上小桶还没有到达最高点时已经离开圆周轨道做抛体运动了.。
