2.3.1 平行线的性质(共24张PPT)
文档属性
| 名称 | 2.3.1 平行线的性质(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览





文档简介
2.3.1平行线的性质
第二章
相交线与平行线
2020-2021北师大版七年级数学下册
1.掌握平行线的性质,会运用两条直线是平行判断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理及计算. (难点)
学习目标
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新课导入
一,平行线的性质
如图,直线a与直线b平行
1.测量同位角∠1 和∠5 的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
探究新知
a
b
d
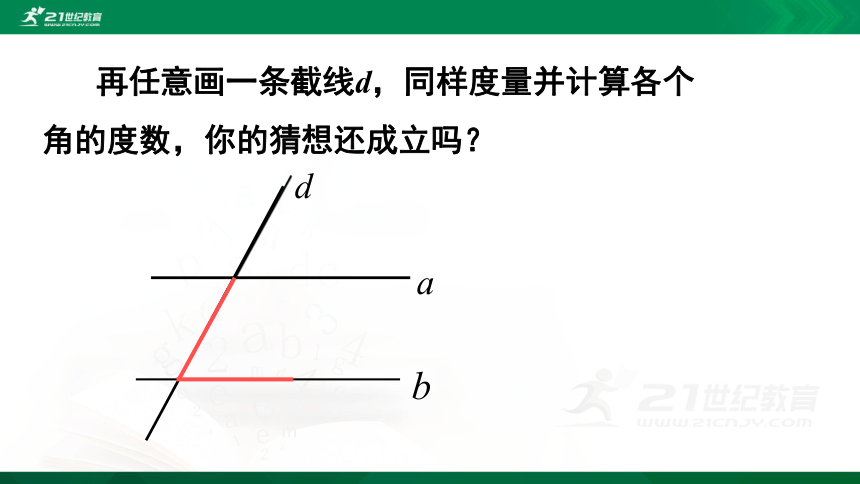
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
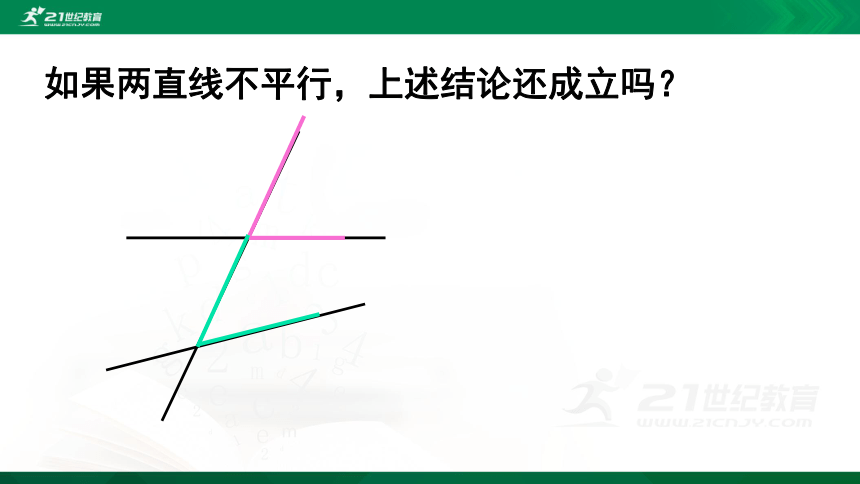
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
总结归纳
应用格式:
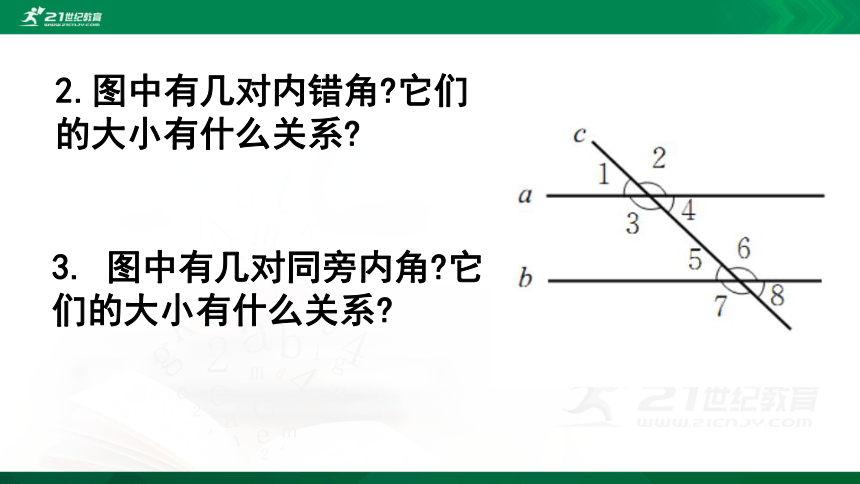
2.图中有几对内错角?它们的大小有什么关系?
3. 图中有几对同旁内角?它们的大小有什么关系?
观察 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想 两条平行线被第三条直线所截,同位角___,
内错角_____,同旁内角_____.
相等
相等
互补
已知:如图,两条直线a,b被第三条直线所截,a//b
求证:?2=?3
证明:∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
论证猜想
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
已知:如图,两条直线a,b被第三条直线所截,a//b
求证:?2+?4=180°
论证猜想
b
1
2
a
c
4
证明: ∵a//b(已知),
∴?1= ?2
(两直线平行,同位角相等).
∵?1+? 4=180°(补角定义),
∴? 2+ ? 4=180°(等量代换).
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∵a∥b(已知)
∴∠2+∠4=180 °
(两直线平行,内错角相等)
应用格式:
总结归纳
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
如图,一束平行光线AB 与DE 射向一个水平镜面后被反射,此时 ∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
做一做
解:(1)相等:∠1=∠3;
∠2 =∠4.
因为AB∥DE 所以∠1=∠3.
又 因为∠1=∠2 ,∠3=∠4,
所以 ∠2=∠4.
因为∠2=∠4
所以 BC∥EF.
(2)平行;
1.如果有两条直线被第三条直线所截,那么必定有( )
(A)内错角相等 (B)同位角相等
(C)同旁内角互补 (D)以上都不对
D
2.∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须 ( )
A. ∠1= ∠2 B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o D .∠1是钝角, ∠2是锐角
C
课堂练习
3.如图,已知AB∥CD,∠A=70°,则∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
C
4.如图,已知a∥b,∠1=65°,则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
C
5.如图,已知AB∥CD,∠1=70°,
则∠2=______,∠3=______,
∠4=______.
70°
70°
110°
6.已知AB∥CD, BE 平分 ∠ABC,
∠CDE=150°,则∠C=______.
120°
7. 已知∠3=45 °,∠1与∠2互余,试说明:AB//CD?
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
8.已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,
求证:AE⊥CE.
证明:因为AB∥CD,
所以∠BAC+∠ACD=180°(两直线平行,同旁内角互补),
又因为AE平分∠BAC,CE平分∠ACD,
所以∠EAC= ∠BAC,∠ECA= ∠ACD,
所以∠EAC+∠ECA= (∠BAC+∠ACD)=90°,
所以∠AEC=180°-90°=90°,
所以AE⊥CE.
9. 如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:因为梯形上.下底互相平行,
所以∠A与∠D互补,∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A
=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
谢谢聆听
第二章
相交线与平行线
2020-2021北师大版七年级数学下册
1.掌握平行线的性质,会运用两条直线是平行判断角相等或互补;(重点)
2.能够根据平行线的性质进行简单的推理及计算. (难点)
学习目标
两直线平行
1.同位角相等
2.内错角相等
3.同旁内角互补
问题 平行线的判定方法是什么?
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新课导入
一,平行线的性质
如图,直线a与直线b平行
1.测量同位角∠1 和∠5 的大小,它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
探究新知
a
b
d
再任意画一条截线d,同样度量并计算各个角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
总结归纳
应用格式:
2.图中有几对内错角?它们的大小有什么关系?
3. 图中有几对同旁内角?它们的大小有什么关系?
观察 各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想 两条平行线被第三条直线所截,同位角___,
内错角_____,同旁内角_____.
相等
相等
互补
已知:如图,两条直线a,b被第三条直线所截,a//b
求证:?2=?3
证明:∵a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
论证猜想
性质2:两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
已知:如图,两条直线a,b被第三条直线所截,a//b
求证:?2+?4=180°
论证猜想
b
1
2
a
c
4
证明: ∵a//b(已知),
∴?1= ?2
(两直线平行,同位角相等).
∵?1+? 4=180°(补角定义),
∴? 2+ ? 4=180°(等量代换).
性质3:两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∵a∥b(已知)
∴∠2+∠4=180 °
(两直线平行,内错角相等)
应用格式:
总结归纳
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
如图,一束平行光线AB 与DE 射向一个水平镜面后被反射,此时 ∠1 =∠2,∠3 =∠4.
(1)∠1 与∠3的大小有什么关系?∠2与∠4 呢?
(2)反射光线BC与EF也平行吗?
做一做
解:(1)相等:∠1=∠3;
∠2 =∠4.
因为AB∥DE 所以∠1=∠3.
又 因为∠1=∠2 ,∠3=∠4,
所以 ∠2=∠4.
因为∠2=∠4
所以 BC∥EF.
(2)平行;
1.如果有两条直线被第三条直线所截,那么必定有( )
(A)内错角相等 (B)同位角相等
(C)同旁内角互补 (D)以上都不对
D
2.∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须 ( )
A. ∠1= ∠2 B. ∠1+∠2=90o
C. 2(∠1+∠2)=360o D .∠1是钝角, ∠2是锐角
C
课堂练习
3.如图,已知AB∥CD,∠A=70°,则∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
C
4.如图,已知a∥b,∠1=65°,则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
C
5.如图,已知AB∥CD,∠1=70°,
则∠2=______,∠3=______,
∠4=______.
70°
70°
110°
6.已知AB∥CD, BE 平分 ∠ABC,
∠CDE=150°,则∠C=______.
120°
7. 已知∠3=45 °,∠1与∠2互余,试说明:AB//CD?
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
8.已知:AB∥CD,AE平分∠BAC,CE平分∠ACD,
求证:AE⊥CE.
证明:因为AB∥CD,
所以∠BAC+∠ACD=180°(两直线平行,同旁内角互补),
又因为AE平分∠BAC,CE平分∠ACD,
所以∠EAC= ∠BAC,∠ECA= ∠ACD,
所以∠EAC+∠ECA= (∠BAC+∠ACD)=90°,
所以∠AEC=180°-90°=90°,
所以AE⊥CE.
9. 如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:因为梯形上.下底互相平行,
所以∠A与∠D互补,∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A
=180°-100°=80°,
∠C= 180 °-∠B=180°-115°=65°.
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
