5.3.1 平行线的性质同步练习(含解析)
文档属性
| 名称 | 5.3.1 平行线的性质同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 00:00:00 | ||
图片预览



文档简介
人教版数学七年级下册 第五章 相交线与平行线
5.3.1 平行线的性质 同步练习
一、单选题
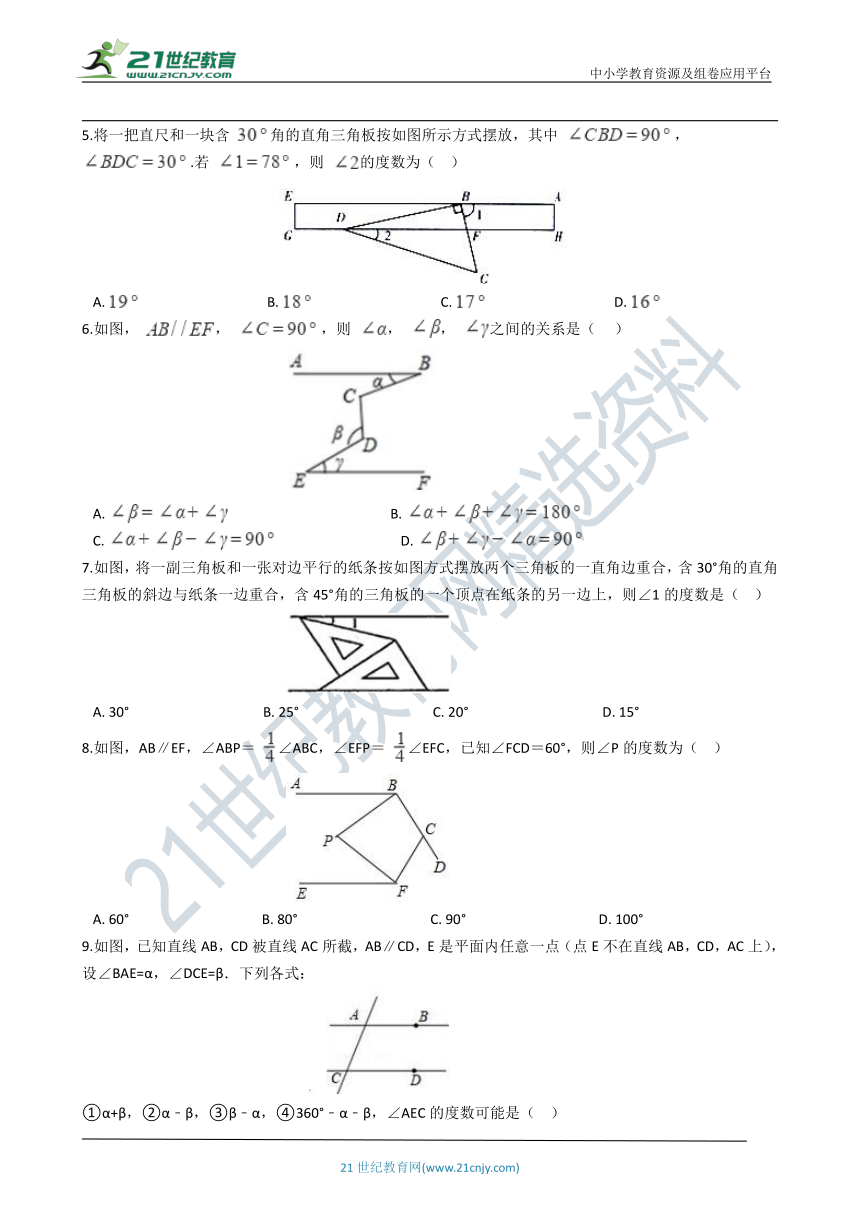
1.如图,直线a,b被直线c所截,且a//b,若∠1=55°,则∠2等于(?? )
A.?35°??????????????????????????????????????B.?45°??????????????????????????????????????C.?55°??????????????????????????????????????D.?125°
2.如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向,则∠BAC的度数是(?? )
A.?85°???????????????????????????????????????B.?80°???????????????????????????????????????C.?90°???????????????????????????????????????D.?95°
3.如图,直线 ,且 于点 ,若 ,则 的度数为(?? )
A.?65°???????????????????????????????????????B.?55°???????????????????????????????????????C.?45°???????????????????????????????????????D.?35°
4.如图,将一副三角板按如图所示的方式摆放,其中两条斜边 , 角的顶点与含 角的直角三角板的直角顶点重合,点E,D,C在同一条直线上,则 的为(??? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
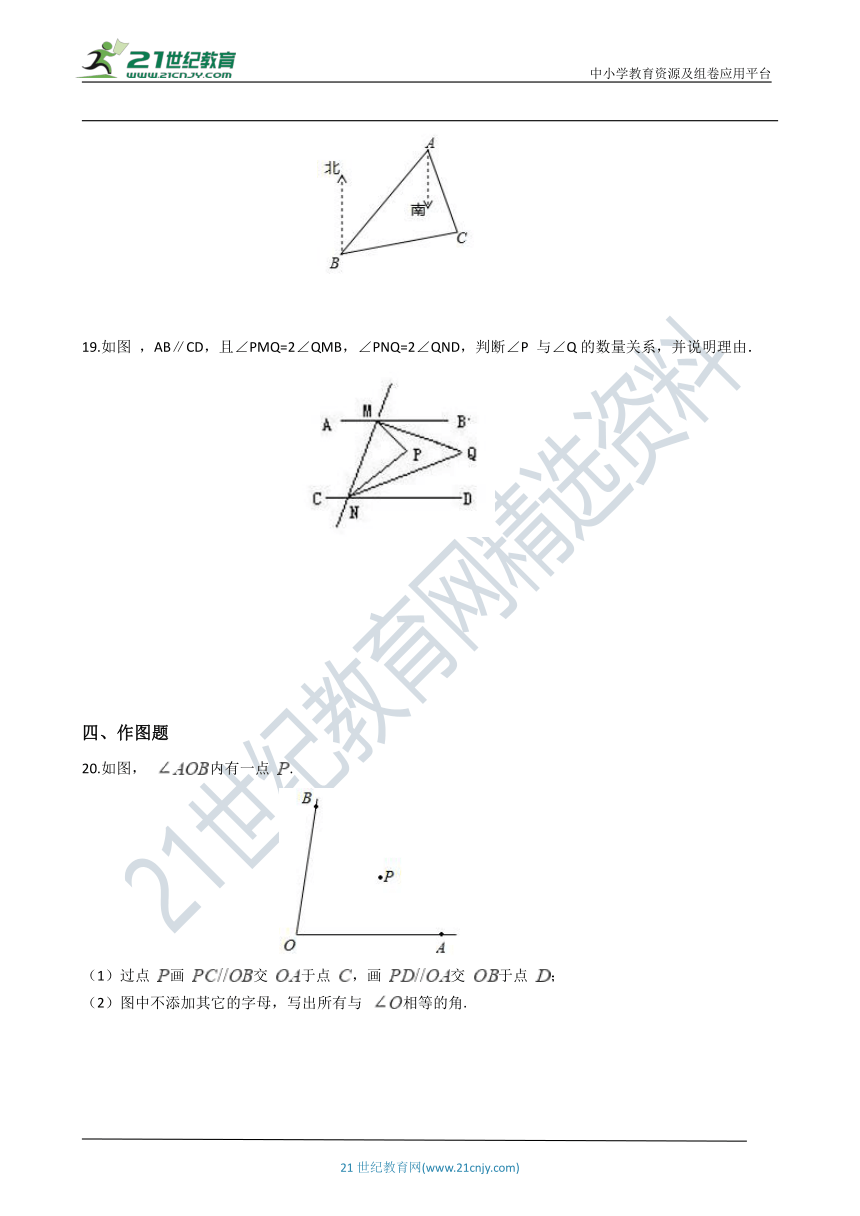
5.将一把直尺和一块含 角的直角三角板按如图所示方式摆放,其中 , .若 ,则 的度数为( ??)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
6.如图, , ,则 , , 之间的关系是(??? )
A.????????????????????????????????????????????????B.?
C.????????????????????????????????????D.?
7.如图,将一副三角板和一张对边平行的纸条按如图方式摆放两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是(?? )
A.?30°???????????????????????????????????????B.?25°???????????????????????????????????????C.?20°???????????????????????????????????????D.?15°
8.如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为(?? )
A.?60°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
9.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是(?? )
A.?①②③??????????????????????????B.?①②④??????????????????????????C.?①③④??????????????????????????D.?①②③④??????? 图4
二、填空题
10.如图,AB∥CD,∠1=50°,∠2=110°,则∠3=________度.
11.如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=________.
12.如图,AB∥CD.EF⊥AB于E,EF交CD于F,已知∠1=58°,则∠2=________.
13.如图,将一副三角板和一张对边平行的纸条按如图方式摆放,则∠α的度数是________.
14.已知∠A与∠B( , )的两边-边平行,另一边互相垂直,且 ,则∠A的度数为________°.
15.问题情境:如图1,已知 , .求 的度数.
(1)经过思考,小敏的思路是:如图2,过P作 ,根据平行线有关性质,可得 ________.???
(2)问题迁移:如图3, ,点P在射线OM上运动, , .
①当点P在A,B两点之间运动时, 、 、 之间有何数量关系?请说明理由.
②如果点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请你直接写出 、 、 之间的数量关系,
(3)问题拓展:如图4, , 是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为________.???
三、解答题
16.如图,有三个论断① ;② ;③ ,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
17.如图所示,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.
18.如图,B处在A处南偏西50°方向,C处在A处的南偏东20°方向,C处在B处的北偏东80°方向,求∠ACB的度数.
19.如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
四、作图题
20.如图, 内有一点 .
(1)过点 画 交 于点 ,画 交 于点 ;
(2)图中不添加其它的字母,写出所有与 相等的角.
五、综合题
21.如图
(1)如图1,要使 , 、 、 应满足的数量关系是________.
(2),直线MN分别与AB、CD交于点M、N,平面内一点P满足 ,
①如图2,若 于点P,判断 与 的数量关系,并说明理由;
②若 , ,求 用含 的式子表示 .
答案解析部分
一、单选题
1.【答案】 C
【解析】根据图示可得:∠1和∠2是同位角,根据两直线平行,同位角相等可得:∠2=∠1=55°.
2.【答案】 C
【解析】∵∠DBA=40°,∠DBC=75°,
∴∠ABC=∠DBC?∠DBA=75°?40°=35°,
∵DB∥EC,
∴∠DBC+∠ECB=180°,
∴∠ECB=180°?∠DBC=180°?75°=105°,
∴∠ACB=∠ECB?∠ACE=105°?50°=55°,
∴∠BAC=180°?∠ACB?∠ABC=180°?55°?35°=90°.
3.【答案】 B
【解析】解:∵ , ,
∴ ,
∵ ,
∴ ,
故答案为:B.
4.【答案】 A
【解析】解:由题意得:∠ADE=45°,∠BAC=30°,
∵AB∥DE,
∴∠BAD=∠ADE=45°,
∴∠CAD=∠BAD-∠BAC=45°-30°=15°;
故答案为:A.
5.【答案】 B
【解析】解:∵EA∥GH ,
∴ .
∴ .
∴ .
故答案为:B.
6.【答案】 C
【解析】解:如图,分别过C、D作AB的平行线CM和DN,
∵ ,
∴ ,
∴ , , ,
∴ ,
又∵ ,
∴ ,
∴ ,
即 ,
故答案为:C.
7.【答案】 D
【解析】如图,过点E作
由题意得:
又
解得
故答案为:D.
8.【答案】 A
【解析】解:过C作CQ∥AB,
∵AB∥EF,
∴AB∥EF∥CQ,
∴∠ABC+∠BCQ=180°,∠EFC+∠FCQ=180°,
∴∠ABC+∠BCF+∠EFC=360°,
∵∠FCD=60°,
∴∠BCF=120°,
∴∠ABC+∠EFC=360°﹣120°=240°,
∵∠ABP= ∠ABC,∠EFP= ∠EFC,
∴∠ABP+∠PFE=60°,
∴∠P=60°.
故答案为:A.
9.【答案】 D
【解析】解:如下图,当E点在直线AB,CD之间并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠AEF+∠FEC=α+β
故①正确
如下图,当E点在直线AB上面并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠FEC-∠AEF=β-α
故③正确
如下图,当E点在直线CD下面并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠AEF-∠FEC=α-β
故②正确
如下图,当E点在直线AB,CD之间并且在AC左边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE+∠AEF=180°?、∠DCE+∠FEC=180°
∴ ∠AEC=∠AEF+∠FEC=180°?-α+180°-β= 360°﹣α﹣β
故④正确
∴①②③④正确
故答案为:D
二、填空题
10.【答案】 60
【解析】解:如图所示:
∵∠2=110°,
∴∠4=70°,
∵AB∥CD,
∴∠5=∠1=50°,
∴∠3=180°?∠4?∠5=60°,
11.【答案】 15°
【解析】∵AB∥CD,∴∠A=∠AFE=30°,∴∠CFE=∠AFE﹣∠AFC=15°,∵CD∥EF,∴∠C=∠CFE=15°,故答案为15°.
12.【答案】 32°
【解析】解:如图,
∵AB∥CD
∴∠1=∠AEH=58°,
∵EF⊥AB,
∴∠2=90°-∠AEH=90°-58°=32°.
故答案为:32°.
13.【答案】 15°
【解析】解:过点O作 ,
由题意得
?
?
故答案为:15°.
14.【答案】 36或96
【解析】解:①如下图:
∵AC//BD,∠E=90°
∴∠A+∠B=90°
∵
∴3∠A=108°
∴∠A=36°
②如下图
∵AC//BD,∠E=90°
∴∠A+∠B=360°-90°=270°
∵
∴3∠A=288°
∴∠A=96°
故答案为:36或96
15.【答案】 (1)252°
(2)解:① = +
理由:如图
如图3,过P作PE//AD交CD于E,
∵AD//BC ,
∴AD//PE//BC ,
∴∠α=∠DPE,∠β=∠CPE ,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
②∠CPD=∠β-∠α
(3)∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn
【解析】解:(1)解:问题情境:如图,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=108°,
∴∠PAB+∠PCD=360°-108°=252°;
故答案为:252°;(2)②解:当P在BA延长线时,∠CPD=∠β-∠α;理由:
如图,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE=∠β-∠α;
当P在BO之间时,∠CPD=∠α-∠β.理由:
如图,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE-∠CPE=∠α-∠β.(3)问题拓展:分别过A2? , A3…,An-1作直线∥A1M,过B1? , B2? , …,Bn-1作直线∥A1M,
由平行线的性质和角的和差关系得∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn.
故答案为:∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn.
三、解答题
16.【答案】 解:答案不唯一,如:选②③作为条件,①作为结论.
已知 .所以 .
已知:∠B=∠D,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C,
∴AB∥CD.
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D.
∴DE∥BF.
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
【解析】根据平行线的性质与判定作答即可。
17.【答案】 解:∵∠1+∠2=90°,CE,DE分别平分∠BCD,∠ADC,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC,∴∠A+∠B=180°,
∵∠B=75°,
∴∠A=180°﹣75°=105°.
【解析】根据已知条件∠1+∠2=90°,CE,DE分别为角平分线,可得一对同旁内角互补,证得AD∥BC;根据两直线平行,同旁内角互补由已知∠B的度数,即可求出∠A的度数.
18.【答案】 解:如图:
由题意得,∠EAB=50°,∠EAC=20°,
则∠BAC=70°,
∵BD∥AE,
∴∠DBA=∠EAB=50°,
又∵∠DBC=80°,
∴∠ABC=30°,
∴∠ACB=180° 70° 30°=80°.
【解析】根据题意和图形,正确画出方向角,根据平行线的性质和三角形内角和定理计算即可.
19.【答案】 解:作QR∥AB,PL∥AB,∴RQ∥CD∥AB,PL∥AB∥CD
∴∠RQM=∠BMQ,∠RQN=∠QND,∠MPL=∠BMP,∠NPL=∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND?,
∴∠PMB=3∠QMB?,∠PND=3∠QND?,
∵∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,
∠MPN=∠MPL+∠NPL=∠BMP+∠PND,
∴∠MPN=3∠MQN,即∠P=3∠Q.
【解析】作QR∥AB,PL∥AB,可得RQ∥CD∥AB,PL∥AB∥CD,根据平行线的性质可得∠RQM=∠BMQ,从而可得∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,同理可得∠MPN=∠MPL+∠NPL=∠BMP+∠PND,结合已知即可求出结论.
四、作图题
20.【答案】 (1)解:如图所示;
(2)解:由题意知: , ,
∴四边形OCPD是平行四边形
∴∠O=∠PCA=∠BDP=∠CPD.
即与 相等的角有∠PCA,∠BDP,∠CPD
【解析】(2)解:∵PC∥OB,∴ ∠O=∠PCA ,
∵PD∥OA,∴ ∠O=∠BDP, ∠PCA=∠CPD,
∴ ∠O=∠PCA=∠BDP=∠CPD ,
即与 相等的角有∠PCA,∠BDP,∠CPD
(1)由题中的几何语言即可画出对应的几何图形;
(2)由题意可知四边形OCPD是平行四边形,结合平行线的性质即可写出与∠O相等的角.
五、综合题
21.【答案】 (1)
(2)解:①作 ,如图:
又 ,
,
又 ,
,
又 ,
,
又 ,
,
又 ,
,
又 ,
,
,
,
即 ;
② 过点P作 ,
又 ,
,
,
,
,
,
又 ,
,
即 ,
又 ,
,
,
即 ;
同理
,
??? ,
,
?综上所述,
【解析】解:(1) ,如图1,过P点作 ,
,
假如 ,
,
,
,
,
要使 ,
.
故答案为: ;
5.3.1 平行线的性质 同步练习
一、单选题
1.如图,直线a,b被直线c所截,且a//b,若∠1=55°,则∠2等于(?? )
A.?35°??????????????????????????????????????B.?45°??????????????????????????????????????C.?55°??????????????????????????????????????D.?125°
2.如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向,则∠BAC的度数是(?? )
A.?85°???????????????????????????????????????B.?80°???????????????????????????????????????C.?90°???????????????????????????????????????D.?95°
3.如图,直线 ,且 于点 ,若 ,则 的度数为(?? )
A.?65°???????????????????????????????????????B.?55°???????????????????????????????????????C.?45°???????????????????????????????????????D.?35°
4.如图,将一副三角板按如图所示的方式摆放,其中两条斜边 , 角的顶点与含 角的直角三角板的直角顶点重合,点E,D,C在同一条直线上,则 的为(??? )
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
5.将一把直尺和一块含 角的直角三角板按如图所示方式摆放,其中 , .若 ,则 的度数为( ??)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
6.如图, , ,则 , , 之间的关系是(??? )
A.????????????????????????????????????????????????B.?
C.????????????????????????????????????D.?
7.如图,将一副三角板和一张对边平行的纸条按如图方式摆放两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是(?? )
A.?30°???????????????????????????????????????B.?25°???????????????????????????????????????C.?20°???????????????????????????????????????D.?15°
8.如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为(?? )
A.?60°??????????????????????????????????????B.?80°??????????????????????????????????????C.?90°??????????????????????????????????????D.?100°
9.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是(?? )
A.?①②③??????????????????????????B.?①②④??????????????????????????C.?①③④??????????????????????????D.?①②③④??????? 图4
二、填空题
10.如图,AB∥CD,∠1=50°,∠2=110°,则∠3=________度.
11.如图,AB∥CD∥EF,若∠A=30°,∠AFC=15°,则∠C=________.
12.如图,AB∥CD.EF⊥AB于E,EF交CD于F,已知∠1=58°,则∠2=________.
13.如图,将一副三角板和一张对边平行的纸条按如图方式摆放,则∠α的度数是________.
14.已知∠A与∠B( , )的两边-边平行,另一边互相垂直,且 ,则∠A的度数为________°.
15.问题情境:如图1,已知 , .求 的度数.
(1)经过思考,小敏的思路是:如图2,过P作 ,根据平行线有关性质,可得 ________.???
(2)问题迁移:如图3, ,点P在射线OM上运动, , .
①当点P在A,B两点之间运动时, 、 、 之间有何数量关系?请说明理由.
②如果点P在A,B两点外侧运动时(点P与点A,B,O三点不重合),请你直接写出 、 、 之间的数量关系,
(3)问题拓展:如图4, , 是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为________.???
三、解答题
16.如图,有三个论断① ;② ;③ ,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
17.如图所示,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.
18.如图,B处在A处南偏西50°方向,C处在A处的南偏东20°方向,C处在B处的北偏东80°方向,求∠ACB的度数.
19.如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
四、作图题
20.如图, 内有一点 .
(1)过点 画 交 于点 ,画 交 于点 ;
(2)图中不添加其它的字母,写出所有与 相等的角.
五、综合题
21.如图
(1)如图1,要使 , 、 、 应满足的数量关系是________.
(2),直线MN分别与AB、CD交于点M、N,平面内一点P满足 ,
①如图2,若 于点P,判断 与 的数量关系,并说明理由;
②若 , ,求 用含 的式子表示 .
答案解析部分
一、单选题
1.【答案】 C
【解析】根据图示可得:∠1和∠2是同位角,根据两直线平行,同位角相等可得:∠2=∠1=55°.
2.【答案】 C
【解析】∵∠DBA=40°,∠DBC=75°,
∴∠ABC=∠DBC?∠DBA=75°?40°=35°,
∵DB∥EC,
∴∠DBC+∠ECB=180°,
∴∠ECB=180°?∠DBC=180°?75°=105°,
∴∠ACB=∠ECB?∠ACE=105°?50°=55°,
∴∠BAC=180°?∠ACB?∠ABC=180°?55°?35°=90°.
3.【答案】 B
【解析】解:∵ , ,
∴ ,
∵ ,
∴ ,
故答案为:B.
4.【答案】 A
【解析】解:由题意得:∠ADE=45°,∠BAC=30°,
∵AB∥DE,
∴∠BAD=∠ADE=45°,
∴∠CAD=∠BAD-∠BAC=45°-30°=15°;
故答案为:A.
5.【答案】 B
【解析】解:∵EA∥GH ,
∴ .
∴ .
∴ .
故答案为:B.
6.【答案】 C
【解析】解:如图,分别过C、D作AB的平行线CM和DN,
∵ ,
∴ ,
∴ , , ,
∴ ,
又∵ ,
∴ ,
∴ ,
即 ,
故答案为:C.
7.【答案】 D
【解析】如图,过点E作
由题意得:
又
解得
故答案为:D.
8.【答案】 A
【解析】解:过C作CQ∥AB,
∵AB∥EF,
∴AB∥EF∥CQ,
∴∠ABC+∠BCQ=180°,∠EFC+∠FCQ=180°,
∴∠ABC+∠BCF+∠EFC=360°,
∵∠FCD=60°,
∴∠BCF=120°,
∴∠ABC+∠EFC=360°﹣120°=240°,
∵∠ABP= ∠ABC,∠EFP= ∠EFC,
∴∠ABP+∠PFE=60°,
∴∠P=60°.
故答案为:A.
9.【答案】 D
【解析】解:如下图,当E点在直线AB,CD之间并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠AEF+∠FEC=α+β
故①正确
如下图,当E点在直线AB上面并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠FEC-∠AEF=β-α
故③正确
如下图,当E点在直线CD下面并且在AC右边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE= ∠AEF?、∠DCE= ∠FEC
∴ ∠AEC=∠AEF-∠FEC=α-β
故②正确
如下图,当E点在直线AB,CD之间并且在AC左边时,作EF//AB
∵ AB∥CD、EF//AB
∴AB∥CD∥EF
∴ ∠BAE+∠AEF=180°?、∠DCE+∠FEC=180°
∴ ∠AEC=∠AEF+∠FEC=180°?-α+180°-β= 360°﹣α﹣β
故④正确
∴①②③④正确
故答案为:D
二、填空题
10.【答案】 60
【解析】解:如图所示:
∵∠2=110°,
∴∠4=70°,
∵AB∥CD,
∴∠5=∠1=50°,
∴∠3=180°?∠4?∠5=60°,
11.【答案】 15°
【解析】∵AB∥CD,∴∠A=∠AFE=30°,∴∠CFE=∠AFE﹣∠AFC=15°,∵CD∥EF,∴∠C=∠CFE=15°,故答案为15°.
12.【答案】 32°
【解析】解:如图,
∵AB∥CD
∴∠1=∠AEH=58°,
∵EF⊥AB,
∴∠2=90°-∠AEH=90°-58°=32°.
故答案为:32°.
13.【答案】 15°
【解析】解:过点O作 ,
由题意得
?
?
故答案为:15°.
14.【答案】 36或96
【解析】解:①如下图:
∵AC//BD,∠E=90°
∴∠A+∠B=90°
∵
∴3∠A=108°
∴∠A=36°
②如下图
∵AC//BD,∠E=90°
∴∠A+∠B=360°-90°=270°
∵
∴3∠A=288°
∴∠A=96°
故答案为:36或96
15.【答案】 (1)252°
(2)解:① = +
理由:如图
如图3,过P作PE//AD交CD于E,
∵AD//BC ,
∴AD//PE//BC ,
∴∠α=∠DPE,∠β=∠CPE ,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;
②∠CPD=∠β-∠α
(3)∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn
【解析】解:(1)解:问题情境:如图,过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠PAB+∠APE=180°,∠PCD+∠CPE=180°,
∵∠APC=108°,
∴∠PAB+∠PCD=360°-108°=252°;
故答案为:252°;(2)②解:当P在BA延长线时,∠CPD=∠β-∠α;理由:
如图,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE=∠β-∠α;
当P在BO之间时,∠CPD=∠α-∠β.理由:
如图,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE-∠CPE=∠α-∠β.(3)问题拓展:分别过A2? , A3…,An-1作直线∥A1M,过B1? , B2? , …,Bn-1作直线∥A1M,
由平行线的性质和角的和差关系得∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn.
故答案为:∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠Bn.
三、解答题
16.【答案】 解:答案不唯一,如:选②③作为条件,①作为结论.
已知 .所以 .
已知:∠B=∠D,∠A=∠C.
求证:∠1=∠2.
证明:∵∠A=∠C,
∴AB∥CD.
∴∠B=∠BFC.
∵∠B=∠D,
∴∠BFC=∠D.
∴DE∥BF.
∴∠DMN=∠BNM.
∵∠1=∠DMN,∠2=∠BNM,
∴∠1=∠2.
【解析】根据平行线的性质与判定作答即可。
17.【答案】 解:∵∠1+∠2=90°,CE,DE分别平分∠BCD,∠ADC,
∴∠ADC+∠BCD=2(∠1+∠2)=180°,
∴AD∥BC,∴∠A+∠B=180°,
∵∠B=75°,
∴∠A=180°﹣75°=105°.
【解析】根据已知条件∠1+∠2=90°,CE,DE分别为角平分线,可得一对同旁内角互补,证得AD∥BC;根据两直线平行,同旁内角互补由已知∠B的度数,即可求出∠A的度数.
18.【答案】 解:如图:
由题意得,∠EAB=50°,∠EAC=20°,
则∠BAC=70°,
∵BD∥AE,
∴∠DBA=∠EAB=50°,
又∵∠DBC=80°,
∴∠ABC=30°,
∴∠ACB=180° 70° 30°=80°.
【解析】根据题意和图形,正确画出方向角,根据平行线的性质和三角形内角和定理计算即可.
19.【答案】 解:作QR∥AB,PL∥AB,∴RQ∥CD∥AB,PL∥AB∥CD
∴∠RQM=∠BMQ,∠RQN=∠QND,∠MPL=∠BMP,∠NPL=∠PND,
∵∠PMQ=2∠QMB,∠PNQ=2∠QND?,
∴∠PMB=3∠QMB?,∠PND=3∠QND?,
∵∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,
∠MPN=∠MPL+∠NPL=∠BMP+∠PND,
∴∠MPN=3∠MQN,即∠P=3∠Q.
【解析】作QR∥AB,PL∥AB,可得RQ∥CD∥AB,PL∥AB∥CD,根据平行线的性质可得∠RQM=∠BMQ,从而可得∠MQN=∠∠RQM+∠RQN=∠BMQ+∠QND,同理可得∠MPN=∠MPL+∠NPL=∠BMP+∠PND,结合已知即可求出结论.
四、作图题
20.【答案】 (1)解:如图所示;
(2)解:由题意知: , ,
∴四边形OCPD是平行四边形
∴∠O=∠PCA=∠BDP=∠CPD.
即与 相等的角有∠PCA,∠BDP,∠CPD
【解析】(2)解:∵PC∥OB,∴ ∠O=∠PCA ,
∵PD∥OA,∴ ∠O=∠BDP, ∠PCA=∠CPD,
∴ ∠O=∠PCA=∠BDP=∠CPD ,
即与 相等的角有∠PCA,∠BDP,∠CPD
(1)由题中的几何语言即可画出对应的几何图形;
(2)由题意可知四边形OCPD是平行四边形,结合平行线的性质即可写出与∠O相等的角.
五、综合题
21.【答案】 (1)
(2)解:①作 ,如图:
又 ,
,
又 ,
,
又 ,
,
又 ,
,
又 ,
,
又 ,
,
,
,
即 ;
② 过点P作 ,
又 ,
,
,
,
,
,
又 ,
,
即 ,
又 ,
,
,
即 ;
同理
,
??? ,
,
?综上所述,
【解析】解:(1) ,如图1,过P点作 ,
,
假如 ,
,
,
,
,
要使 ,
.
故答案为: ;
