5.3.2 命题、定理、证明同步练习(含解析)
文档属性
| 名称 | 5.3.2 命题、定理、证明同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 21:10:31 | ||
图片预览



文档简介
人教版数学七年级下册 第五章 相交线与平行线
5.3.2 命题、定理、证明 同步练习
一、单选题
1.下列语句中不是命题的有( ??)
⑴两点之间,线段最短; (2)连接A、B两点;(3)鸟是动物;(4)不相交的两条直线叫做平行线;(5)无论a为怎样的有理数,式子a2+1的值都是正数吗?
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.命题“等角的补角相等”中,“等角的补角”是命题的(?? )
A.?条件部分????????????????B.?是条件,也是结论????????????????C.?结论部分????????????????D.?不是条件,也不是结论
3.下列语句中,不是命题的是 ( ?????)
A.?若两角之和为90°,则这两个角互余。????????????????B.?同角的余角相等。
C.?画线段的中垂线。??????????????????????????????????????????????D.?相等的角是对顶角。
4.下列命题中,为真命题的是(?? )
A.?对顶角相等????????????B.?同位角相等????????????C.?若a2=b2 , 则a=b????????????D.?若a>b,则-2a>-2b
5.下列命题中是真命题的是(?? )
A.?相等的角是对顶角??????????????????????????????????????????????B.?数轴上的点与实数一一对应
C.?同旁内角互补?????????????????????????????????????????????????????D.?无理数就是开方开不尽得数
二、填空题
6.把命题“在同一平面内,垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式为________.
7.命题“对顶角相等”的逆命题是________ ,这是一个________(填真或假)命题.
8.命题“内错角相等”是________命题(填“真”、“假”).
9.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出________个正确的命题.
三、解答题
10.下列各命题的条件是什么?结论是什么?
(1)两直线平行,同位角相等;
(2)过一点有且只有一条直线与已知直线平行.
11.下列语句哪些是命题?对于命题,请先将它改写为“如果……那么……”的形式,再找出命题的条件和结论,并指出是真命题还是假命题,并说明为什么是假命题.
(1)小亮今年上八年级,明年一定上九年级;
(2)作一条线段的垂直平分线;
(3)互为倒数的两个数的积为1;
(4)内错角相等;
(5)不等式的两边同时乘以一个数,不等号的方向改变.
12.下列命题中,哪些是真命题?哪些是假命题?
①内错角相等;
②两直线平行,同旁内角互补;
③若x=2,则x+1>1;
④不等式两边同时乘以或除以一个负数,不等号应改变方向;
⑤三角形两边之和大于第三边.
13.如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
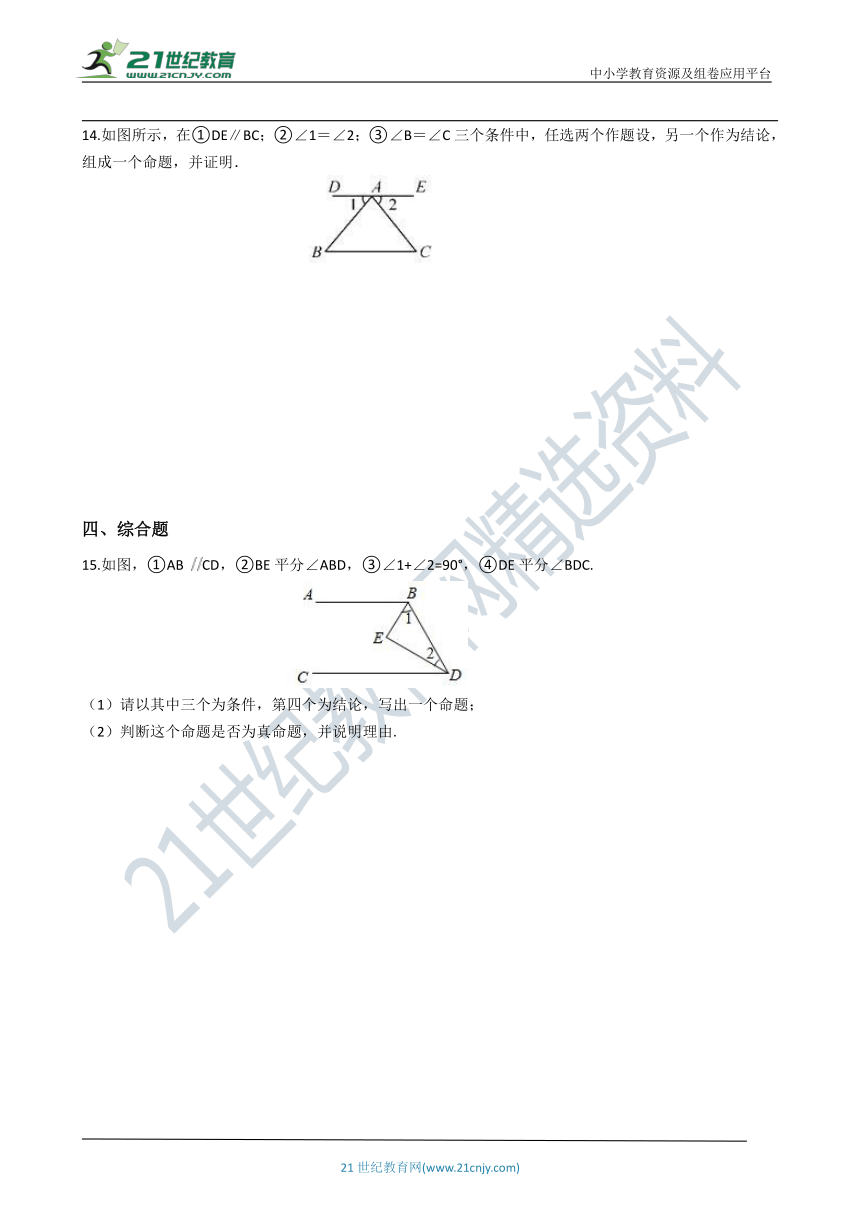
14.如图所示,在①DE∥BC;②∠1=∠2;③∠B=∠C三个条件中,任选两个作题设,另一个作为结论,组成一个命题,并证明.
四、综合题
15.如图,①AB CD,②BE平分∠ABD,③∠1+∠2=90°,④DE平分∠BDC.
(1)请以其中三个为条件,第四个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
答案解析部分
一、单选题
1.【答案】 C
【解析】两点之间,线段最短,所以(1)为命题;
连接A、B两点,它为描述性语言,所以(2)不是命题;
鸟是动物,所以(3)为命题;
不相交的两条直线叫做平行线,所以(4)为命题;
无论a为怎样的有理数,式子a2+1的值都是正数吗?它为疑问句,所以(5)不是命题.
故答案为:C.
2.【答案】 A
【解析】解:命题“等角的补角相等”: 题设是两个角是等角的补角, 结论是这两个角相等,故答案为:A.
3.【答案】 C
【解析】命题就是判断一件事情的语句.
4.【答案】 A
【解析】解:A.对顶角相等,正确,为真命题;
B.两直线平行,同位角相等,错误,为假命题;
C.若a2=b2 , 则a=b或a=-b,错误,为假命题;
D.若a>b,则-2a<-2b,错误,为假命题。
故答案为:A.
5.【答案】 B
【解析】解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、π是无理数,但不是开方开不尽的数,故此命题是假命题;.
故答案为:B.
二、填空题
6.【答案】 在同一平面内,如果两条直线都垂直于同一直线,那么这两直线互相平行
【解析】解:“在同一平面内,垂直于同一条直线的两条直线互相平行”改写成“如果???,那么???”的形式为:“在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行”.
7.【答案】 相等的两个角是对顶角;假
【解析】解:“对顶角相等”的逆命题是相等的角是对顶角,该逆命题是一个假命题.
8.【答案】 假
【解析】∵两直线平行,内错角相等,
∴若两直线不平行,内错角不相等,
∴此命题为假命题,
故答案为:假.
9.【答案】 3
【解析】(1)共有:①②作为条件,③作为结论,
①③作为条件,②作为结论,
②③作为条件,①作为结论,3种情况,都是真命题,
故可以写出3个正确的命题;
故答案为3.
三、解答题
10.【答案】 (1)解:条件是两直线平行;结论是同位角相等。
(2)解:条件是直线外有一点,过这一点做一条直线和已知直线平行;结论是这样的平行线有且只有一条。
【解析】命题都由条件和结论两部分组成,常可写成“如果…那么…”的形式,即“如果p,那么q”的形式,p是条件,q是结论。本题重在区分命题的条件和结论。
11.【答案】 (1)解:如果小亮今年上八年级,那么明年一定上九年级。条件是小亮今年上八年级;结论是明年一定上九年级。有可能留级,所以是假命题。
(2)解:不是命题。
(3)解:如果两个数互为倒数,那么它们的积为1。条件是两个数互为倒数;结论是它们的积为1。是真命题。
(4)解:如果两个角是内错角,那么它们相等。条件是两个角是内错角;结论是它们相等。因为两直线不一定平行,所以是假命题。
(5)解:如果不等式的两边同时乘以一个数,那么不等号的方向改变。条件是不等式的两边同时乘以一个数;结论是不等号的方向改变。只有乘以的是负数才改变,乘以正数不改变,所以是假命题。
【解析】命题是可以判断真假的语句,疑问句、感叹句、祈使句一般都不是命题,所以(2)不是命题。命题一般由条件和结论两部分组成,一般可改写成“如果…,那么…”,如果是条件,那么是结论。
12.【答案】 解:①内错角相等是假命题,应该是两直线平行,内错角相等.
②两直线平行,同旁内角互补,真命题;
③若x=2,则:x+1>1,真命题;
④不等式两边同时乘以或除以一个负数,不等号应改变方向,真命题.
⑤三角形两边之和大于第三边,真命题.
故由分析可知,真命题是②③④⑤,假命题是①.
【解析】命题是可以判断真假的语句,判断出是正确的命题为真命题,判断结论不正确的为假命题。
13.【答案】 解:已知:如图,AB⊥BC、CD⊥BC,BE∥CF.
求证:∠1=∠2.
证明:∵AB⊥BC、CD⊥BC,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC?∠EBC=∠DCB?∠FCB,
∴∠1=∠2.
【解析】选择两个条件作为题设,即为已知条件;另外一个条件为结论,即为证明的结论。根据任选的题设和结论进行证明即可。
?
14.【答案】 解:已知,DE∥BC,∠1=∠2.
求证:∠B=∠C.
证明:∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠1=∠2,
∴∠B=∠C
【解析】命题由题设和结论组成,根据选取的两个条件是否可以推出第三个条件,即可证明其是否组成一个命题。
四、综合题
15.【答案】 (1)解:由题意可得:条件②③④,结论:①;条件①③④,结论:②;条件①②④,结论:③;条件①②③,结论:④.
(2)解:当选取条件②③④,结论:①时
∵BE平分∠ABD,DE平分∠BDC
∴∠ABE=∠1,∠CDE=∠2
又∵∠1+∠2=90°
∴∠ABE+∠CDE+∠1+∠2=180°
∴AB CD
当选取条件①③④,结论:②时
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∵∠1+∠2=90°
∴∠ABE+∠CDE=90°
又∵DE平分∠BDC
∴∠CDE=∠2
∴∠ABE+∠2=90°
∴∠ABE=∠1
∴BE平分∠ABD
当选取条件①②④,结论:③时
∵BE平分∠ABD,DE平分∠BDC
∴∠ABE=∠1,∠CDE=∠2
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∴2∠1+2∠2=180°
∴∠1+∠2=90°
当选取条件①②③,结论:④时
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∵∠1+∠2=90°
∴∠ABE+∠CDE=90°
又∵BE平分∠ABD
∴∠ABE=∠1
∴∠1+∠CDE=90°
∴∠CDE=∠2
∴DE平分∠BDC
【解析】(1)根据题意可得出有四种情况,分别为:条件②③④,结论:①;条件①③④,结论:②;条件①②④,结论:③;条件①②③,结论:④.(2)条件为②③④时,可通过内错角互补证出结论①成立,故为真命题;条件为①③④,①②④和①②③时,可通过两条直线平行,内错角互补等量代换证出相应结论成立,故都为真命题.
5.3.2 命题、定理、证明 同步练习
一、单选题
1.下列语句中不是命题的有( ??)
⑴两点之间,线段最短; (2)连接A、B两点;(3)鸟是动物;(4)不相交的两条直线叫做平行线;(5)无论a为怎样的有理数,式子a2+1的值都是正数吗?
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
2.命题“等角的补角相等”中,“等角的补角”是命题的(?? )
A.?条件部分????????????????B.?是条件,也是结论????????????????C.?结论部分????????????????D.?不是条件,也不是结论
3.下列语句中,不是命题的是 ( ?????)
A.?若两角之和为90°,则这两个角互余。????????????????B.?同角的余角相等。
C.?画线段的中垂线。??????????????????????????????????????????????D.?相等的角是对顶角。
4.下列命题中,为真命题的是(?? )
A.?对顶角相等????????????B.?同位角相等????????????C.?若a2=b2 , 则a=b????????????D.?若a>b,则-2a>-2b
5.下列命题中是真命题的是(?? )
A.?相等的角是对顶角??????????????????????????????????????????????B.?数轴上的点与实数一一对应
C.?同旁内角互补?????????????????????????????????????????????????????D.?无理数就是开方开不尽得数
二、填空题
6.把命题“在同一平面内,垂直于同一条直线的两条直线平行”改写成“如果……那么……”的形式为________.
7.命题“对顶角相等”的逆命题是________ ,这是一个________(填真或假)命题.
8.命题“内错角相等”是________命题(填“真”、“假”).
9.如图,在四边形ABCD中,给出了下列三个论断:①对角线AC平分∠BAD;②CD=BC;③∠D+∠B=180°.在上述三个论断中,若以其中两个论断作为条件,另外一个论断作为结论,则可以得出________个正确的命题.
三、解答题
10.下列各命题的条件是什么?结论是什么?
(1)两直线平行,同位角相等;
(2)过一点有且只有一条直线与已知直线平行.
11.下列语句哪些是命题?对于命题,请先将它改写为“如果……那么……”的形式,再找出命题的条件和结论,并指出是真命题还是假命题,并说明为什么是假命题.
(1)小亮今年上八年级,明年一定上九年级;
(2)作一条线段的垂直平分线;
(3)互为倒数的两个数的积为1;
(4)内错角相等;
(5)不等式的两边同时乘以一个数,不等号的方向改变.
12.下列命题中,哪些是真命题?哪些是假命题?
①内错角相等;
②两直线平行,同旁内角互补;
③若x=2,则x+1>1;
④不等式两边同时乘以或除以一个负数,不等号应改变方向;
⑤三角形两边之和大于第三边.
13.如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截.在下面三个条件中,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并证明.
①AB⊥BC,CD⊥BC,②BE∥CF,③∠1=∠2.
14.如图所示,在①DE∥BC;②∠1=∠2;③∠B=∠C三个条件中,任选两个作题设,另一个作为结论,组成一个命题,并证明.
四、综合题
15.如图,①AB CD,②BE平分∠ABD,③∠1+∠2=90°,④DE平分∠BDC.
(1)请以其中三个为条件,第四个为结论,写出一个命题;
(2)判断这个命题是否为真命题,并说明理由.
答案解析部分
一、单选题
1.【答案】 C
【解析】两点之间,线段最短,所以(1)为命题;
连接A、B两点,它为描述性语言,所以(2)不是命题;
鸟是动物,所以(3)为命题;
不相交的两条直线叫做平行线,所以(4)为命题;
无论a为怎样的有理数,式子a2+1的值都是正数吗?它为疑问句,所以(5)不是命题.
故答案为:C.
2.【答案】 A
【解析】解:命题“等角的补角相等”: 题设是两个角是等角的补角, 结论是这两个角相等,故答案为:A.
3.【答案】 C
【解析】命题就是判断一件事情的语句.
4.【答案】 A
【解析】解:A.对顶角相等,正确,为真命题;
B.两直线平行,同位角相等,错误,为假命题;
C.若a2=b2 , 则a=b或a=-b,错误,为假命题;
D.若a>b,则-2a<-2b,错误,为假命题。
故答案为:A.
5.【答案】 B
【解析】解:A、相等的角不一定是对顶角,故此命题是假命题;
B、数轴上的点与实数一一对应,故此命题是真命题;
C、两直线平行,同旁内角互补,故此命题是假命题;
D、π是无理数,但不是开方开不尽的数,故此命题是假命题;.
故答案为:B.
二、填空题
6.【答案】 在同一平面内,如果两条直线都垂直于同一直线,那么这两直线互相平行
【解析】解:“在同一平面内,垂直于同一条直线的两条直线互相平行”改写成“如果???,那么???”的形式为:“在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行”.
7.【答案】 相等的两个角是对顶角;假
【解析】解:“对顶角相等”的逆命题是相等的角是对顶角,该逆命题是一个假命题.
8.【答案】 假
【解析】∵两直线平行,内错角相等,
∴若两直线不平行,内错角不相等,
∴此命题为假命题,
故答案为:假.
9.【答案】 3
【解析】(1)共有:①②作为条件,③作为结论,
①③作为条件,②作为结论,
②③作为条件,①作为结论,3种情况,都是真命题,
故可以写出3个正确的命题;
故答案为3.
三、解答题
10.【答案】 (1)解:条件是两直线平行;结论是同位角相等。
(2)解:条件是直线外有一点,过这一点做一条直线和已知直线平行;结论是这样的平行线有且只有一条。
【解析】命题都由条件和结论两部分组成,常可写成“如果…那么…”的形式,即“如果p,那么q”的形式,p是条件,q是结论。本题重在区分命题的条件和结论。
11.【答案】 (1)解:如果小亮今年上八年级,那么明年一定上九年级。条件是小亮今年上八年级;结论是明年一定上九年级。有可能留级,所以是假命题。
(2)解:不是命题。
(3)解:如果两个数互为倒数,那么它们的积为1。条件是两个数互为倒数;结论是它们的积为1。是真命题。
(4)解:如果两个角是内错角,那么它们相等。条件是两个角是内错角;结论是它们相等。因为两直线不一定平行,所以是假命题。
(5)解:如果不等式的两边同时乘以一个数,那么不等号的方向改变。条件是不等式的两边同时乘以一个数;结论是不等号的方向改变。只有乘以的是负数才改变,乘以正数不改变,所以是假命题。
【解析】命题是可以判断真假的语句,疑问句、感叹句、祈使句一般都不是命题,所以(2)不是命题。命题一般由条件和结论两部分组成,一般可改写成“如果…,那么…”,如果是条件,那么是结论。
12.【答案】 解:①内错角相等是假命题,应该是两直线平行,内错角相等.
②两直线平行,同旁内角互补,真命题;
③若x=2,则:x+1>1,真命题;
④不等式两边同时乘以或除以一个负数,不等号应改变方向,真命题.
⑤三角形两边之和大于第三边,真命题.
故由分析可知,真命题是②③④⑤,假命题是①.
【解析】命题是可以判断真假的语句,判断出是正确的命题为真命题,判断结论不正确的为假命题。
13.【答案】 解:已知:如图,AB⊥BC、CD⊥BC,BE∥CF.
求证:∠1=∠2.
证明:∵AB⊥BC、CD⊥BC,
∴∠ABC=∠DCB,
又∵BE∥CF,
∴∠EBC=∠FCB,
∴∠ABC?∠EBC=∠DCB?∠FCB,
∴∠1=∠2.
【解析】选择两个条件作为题设,即为已知条件;另外一个条件为结论,即为证明的结论。根据任选的题设和结论进行证明即可。
?
14.【答案】 解:已知,DE∥BC,∠1=∠2.
求证:∠B=∠C.
证明:∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠1=∠2,
∴∠B=∠C
【解析】命题由题设和结论组成,根据选取的两个条件是否可以推出第三个条件,即可证明其是否组成一个命题。
四、综合题
15.【答案】 (1)解:由题意可得:条件②③④,结论:①;条件①③④,结论:②;条件①②④,结论:③;条件①②③,结论:④.
(2)解:当选取条件②③④,结论:①时
∵BE平分∠ABD,DE平分∠BDC
∴∠ABE=∠1,∠CDE=∠2
又∵∠1+∠2=90°
∴∠ABE+∠CDE+∠1+∠2=180°
∴AB CD
当选取条件①③④,结论:②时
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∵∠1+∠2=90°
∴∠ABE+∠CDE=90°
又∵DE平分∠BDC
∴∠CDE=∠2
∴∠ABE+∠2=90°
∴∠ABE=∠1
∴BE平分∠ABD
当选取条件①②④,结论:③时
∵BE平分∠ABD,DE平分∠BDC
∴∠ABE=∠1,∠CDE=∠2
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∴2∠1+2∠2=180°
∴∠1+∠2=90°
当选取条件①②③,结论:④时
∵AB CD
∴∠ABE+∠CDE+∠1+∠2=180°
∵∠1+∠2=90°
∴∠ABE+∠CDE=90°
又∵BE平分∠ABD
∴∠ABE=∠1
∴∠1+∠CDE=90°
∴∠CDE=∠2
∴DE平分∠BDC
【解析】(1)根据题意可得出有四种情况,分别为:条件②③④,结论:①;条件①③④,结论:②;条件①②④,结论:③;条件①②③,结论:④.(2)条件为②③④时,可通过内错角互补证出结论①成立,故为真命题;条件为①③④,①②④和①②③时,可通过两条直线平行,内错角互补等量代换证出相应结论成立,故都为真命题.
