5.4 平移同步练习(含解析)
图片预览
文档简介
人教版数学七年级下册 第五章 相交线与平行线 5.4 平移 同步练习
一、单选题
1.下列图形中,不能由“基本图案”(小四边形)经过平移得到的图形为(?? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.下列四幅图案中,能通过平移图得到的是(? )
A.??????????????????B.??????????????????C.??????????????????D.?
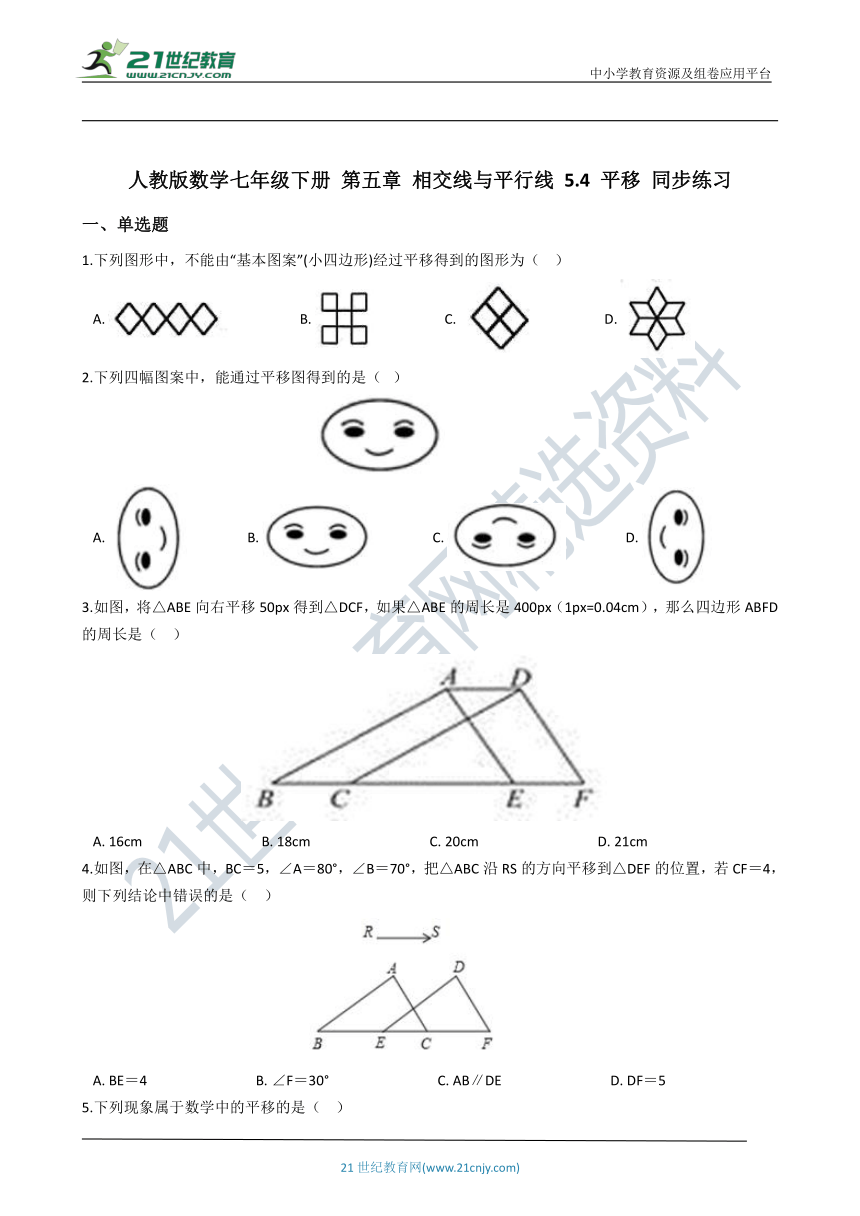
3.如图,将△ABE向右平移50px得到△DCF,如果△ABE的周长是400px(1px=0.04cm),那么四边形ABFD的周长是(?? )
A.?16cm??????????????????????????????????B.?18cm??????????????????????????????????C.?20cm??????????????????????????????????D.?21cm
4.如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )
?
A.?BE=4???????????????????????????????B.?∠F=30°???????????????????????????????C.?AB∥DE???????????????????????????????D.?DF=5
5.下列现象属于数学中的平移的是(?? )
A.?树叶从树上随风飘落???????????????????????????????????????????B.?升降电梯由一楼升到顶楼
C.?汽车方向盘的转动??????????????????????????????????????????????D.?“神舟”号卫星绕地球运动
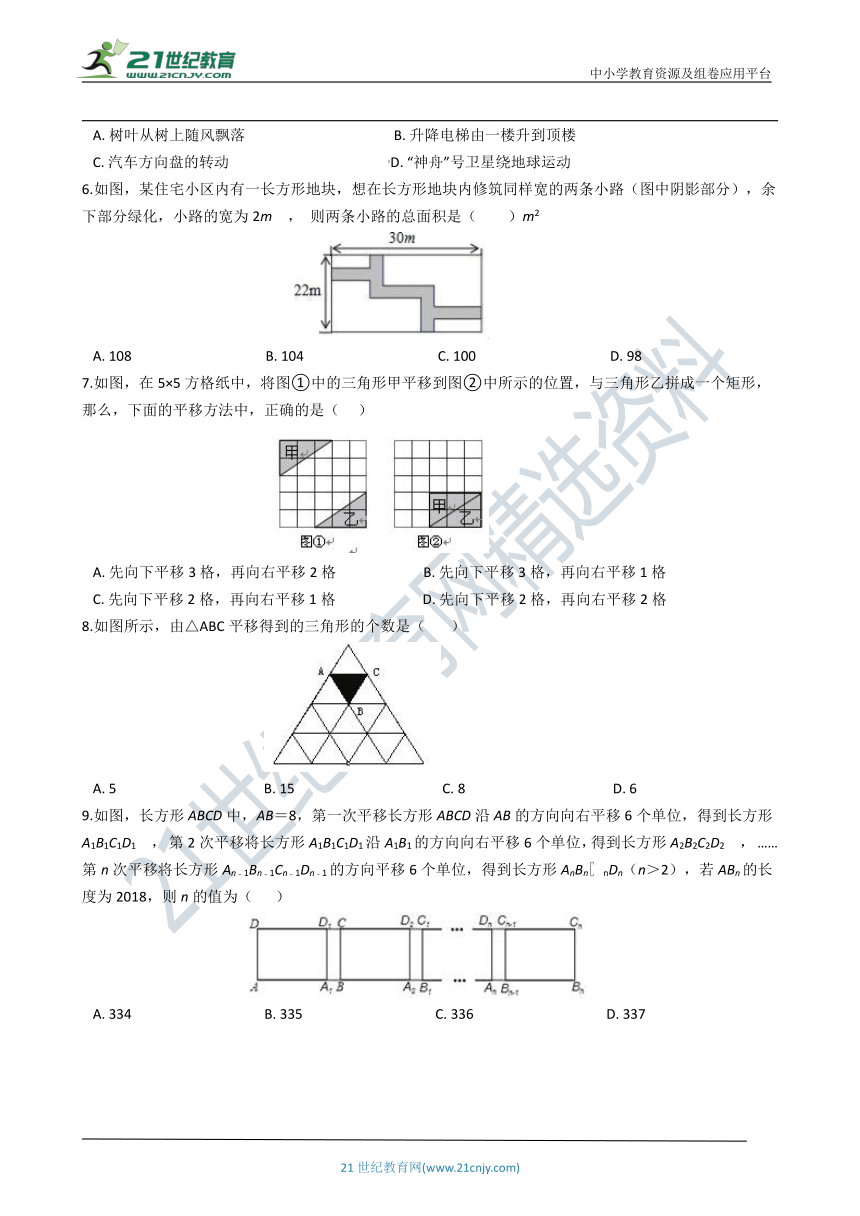
6.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2
A.?108???????????????????????????????????????B.?104???????????????????????????????????????C.?100???????????????????????????????????????D.?98
7.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是(??? )
A.?先向下平移3格,再向右平移2格?????????????????????????B.?先向下平移3格,再向右平移1格
C.?先向下平移2格,再向右平移1格?????????????????????????D.?先向下平移2格,再向右平移2格
8.如图所示,由△ABC平移得到的三角形的个数是(? ????)
A.?5???????????????????????????????????????????B.?15???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
9.如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn?nDn(n>2),若ABn的长度为2018,则n的值为(?? )
A.?334??????????????????????????????????????B.?335??????????????????????????????????????C.?336??????????????????????????????????????D.?337
二、填空题
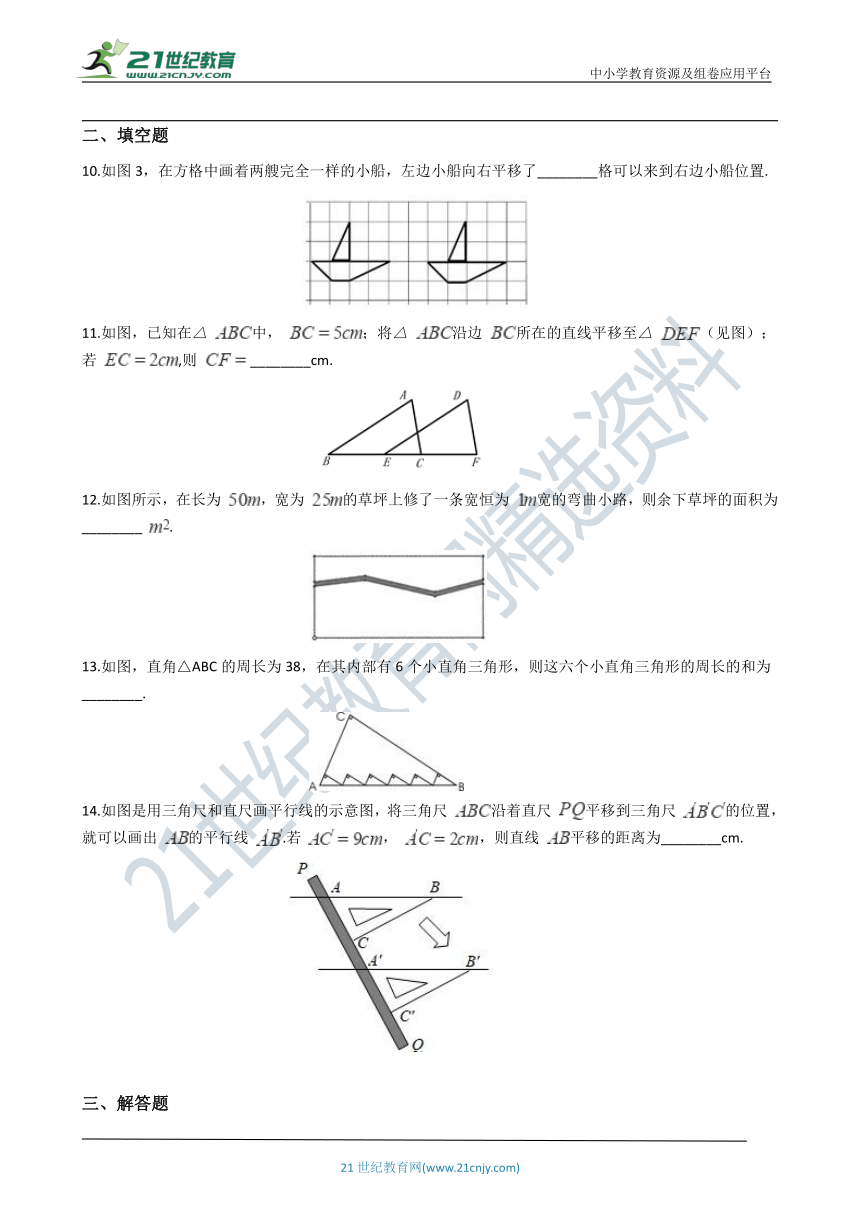
10.如图3,在方格中画着两艘完全一样的小船,左边小船向右平移了________格可以来到右边小船位置.
11.如图,已知在△ 中, ;将△ 沿边 所在的直线平移至△ (见图);若 ,则 ________cm.
12.如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为________ .
13.如图,直角△ABC的周长为38,在其内部有6个小直角三角形,则这六个小直角三角形的周长的和为________.
14.如图是用三角尺和直尺画平行线的示意图,将三角尺 沿着直尺 平移到三角尺 的位置,就可以画出 的平行线 .若 , ,则直线 平移的距离为________cm.
三、解答题
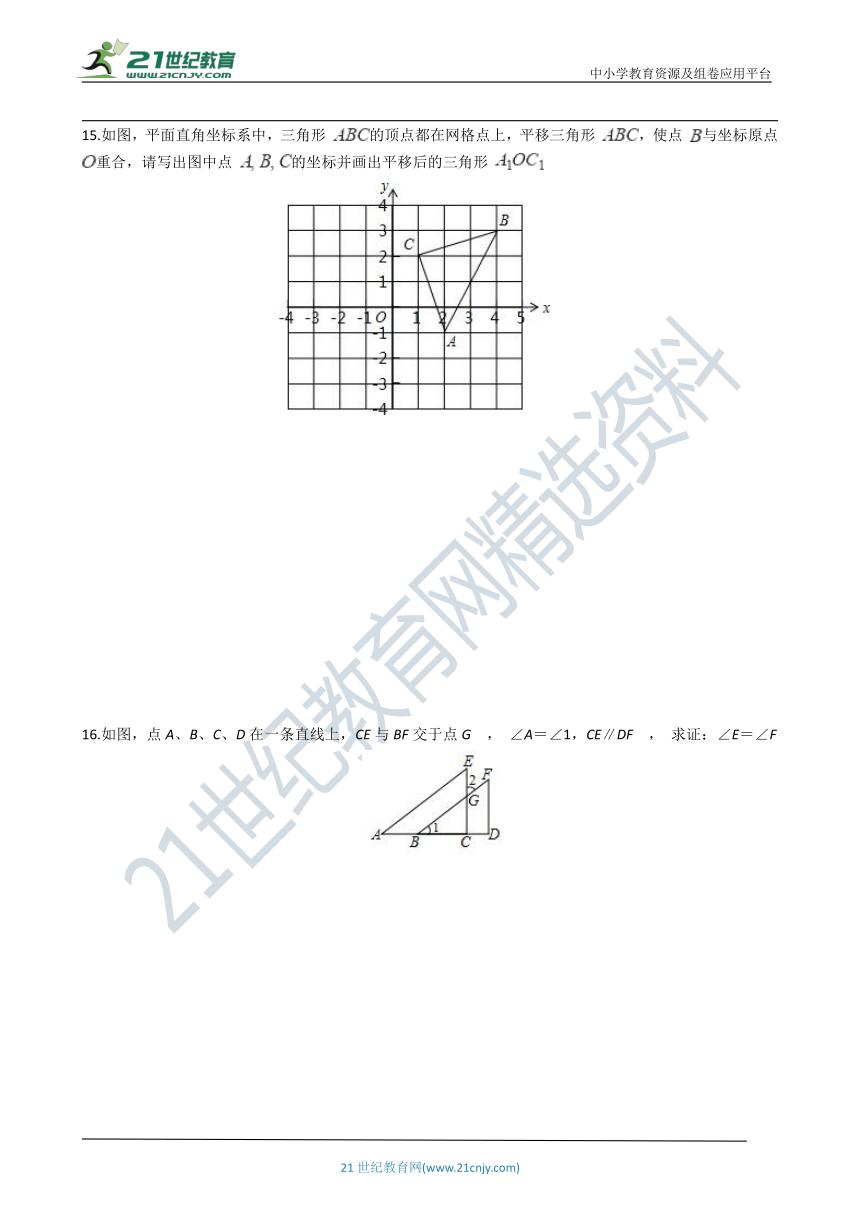
15.如图,平面直角坐标系中,三角形 的顶点都在网格点上,平移三角形 ,使点 与坐标原点 重合,请写出图中点 的坐标并画出平移后的三角形
16.如图,点A、B、C、D在一条直线上,CE与BF交于点G , ∠A=∠1,CE∥DF , 求证:∠E=∠F
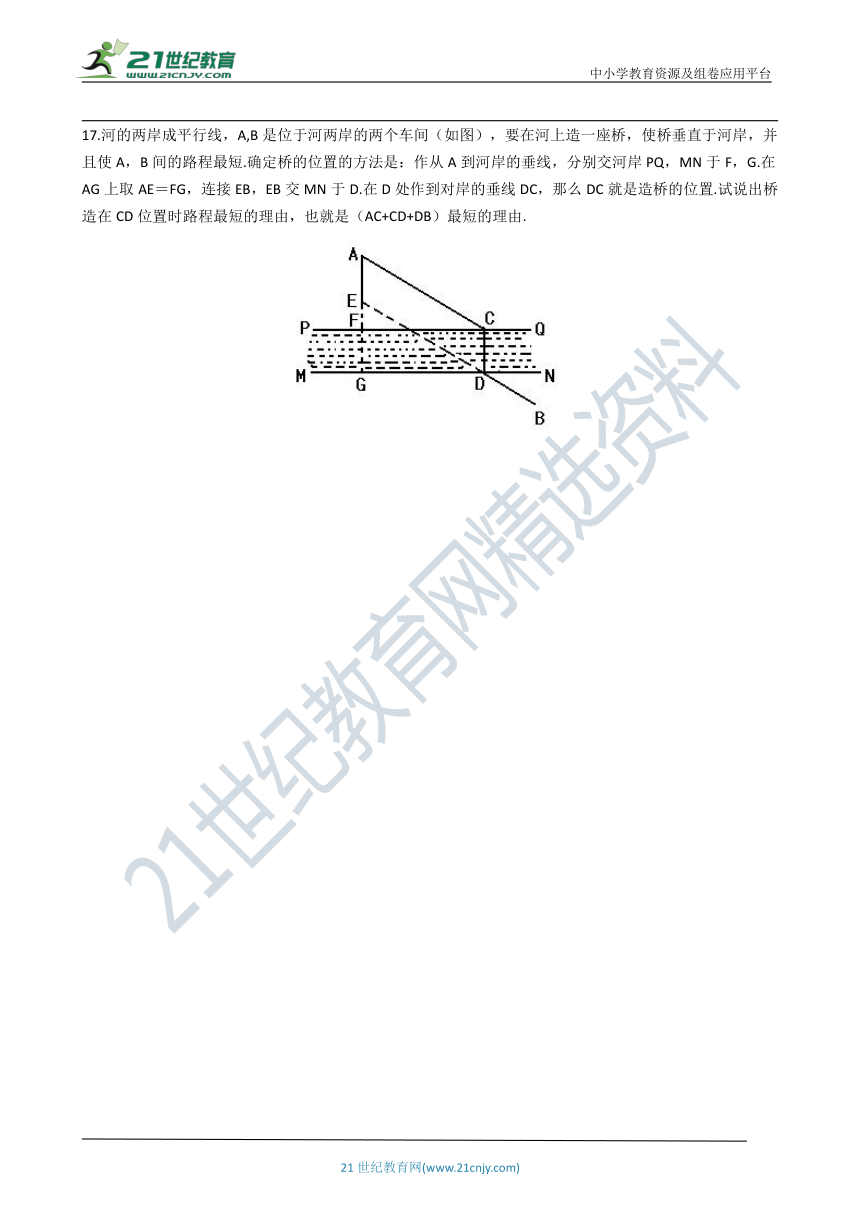
17.河的两岸成平行线,A,B是位于河两岸的两个车间(如图),要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法是:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB,EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.试说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:观察图象可知,选项A,B,C都是可以由基本图形平移得到,
选项D是旋转变换图形,不符合题意,
故答案为:D.
2.【答案】 B
【解析】解:平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移;
观察四个选项可知,只有选项B能通过平移图得到,
故答案为:B.
3.【答案】 C
【解析】∵1px?=?0.04cm,
∴50px=2cm,400px=16cm,
∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF
=AB+BE+AE+AD+EF
=△ABE的周长+AD+EF.
∵平移距离为2cm,
∴AD=EF=2cm,
∵△ABE的周长是16cm,
∴四边形ABFD的周长=16+2+2=20cm.
故答案为:C.
4.【答案】 D
【解析】解:∵把△ABC沿RS的方向平移到△DEF的位置,BC=5,∠A=80°,∠B=70°,
∴CF=BE=4,∠F=∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣70°=30°,AB∥DE,
∴A、B、C正确,D错误.
故答案为:D.
5.【答案】 B
【解析】A.树叶从树上随风飘落,不属于平移;
B.升降电梯由一楼升到顶楼属于平移;
C.汽车方向盘的转动属于旋转;
D. “神舟”号卫星绕地球运动属于旋转;
故答案为:B.
6.【答案】 C
【解析】解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故答案为:C .
7.【答案】 A
【解析】解:平移是先向下平移3格,再向右平移2格.
故答案为:A.
8.【答案】 A
【解析】△ABC经过平移后得到的三角形有一个顶角向下,图中这样的三角形有5个,即得A.
9.【答案】 B
【解析】∵AB=8,第1次平移将矩形ABCD沿AB的方向向右平移6个单位,得到矩形A1B1C1D1 ,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移6个单位,得到矩形A2B2C2D2…,
∴AA1=6,A1A2=6,A2B1=A1B1﹣A1A2=8﹣6=2,
∴AB1=AA1+A1A2+A2B1=6+6+2=14,
∴AB2的长为:6+6+8=20;
∵AB1=2×6+2=14,AB2=3×6+2=20,
∴ABn=(n+1)×6+2=2018,
解得:n=335.
故答案为:B.
10.【答案】 6
【解析】解:如图,
点A平移到点D,
∴左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
11.【答案】 3
【解析】∵将△ABC沿边BC所在的直线平移至△DEF,
∴BE=CF=BC?EC=5?2=3cm,
故答案为3.
12.【答案】 1200
【解析】长方形的长为50m,宽为(25-1).余下草坪的面积为:50×(25-1)=1200m2.
故答案为:1200.
13.【答案】 38
【解析】解:由平移的性质,6个小直角三角形较长的直角边平移后等于BC边,
较短的直角边平移后等于AC边,
斜边之和等于AB边长,
所以,6个小直角三角形的周长之和=Rt△ACB的周长,
∵直角三角形ACB的周长为38,
∴这6个小直角三角形的周长之和=38.
故答案为:38.
14.【答案】 5.5
【解析】解:AC+A′C′=AC′-A′C=9-2=7(cm),
A′C′=7÷2=3.5(cm),
CC′=A′C+A′C′=2+3.5=5.5(cm).
故直线AB平移的距离为5.5cm.
故答案为:5.5.
三、解答题
15.【答案】 解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1 , C1 , 不标的扣一分。
【解析】(1)根据点在坐标系里的位置,写出点的坐标,即可;
(2)由点B平移后与坐标原点O重合,可知,三角形先向左平移4个单位,再向下平移3个单位得到新的三角形.
16.【答案】 证明:∵CE∥DF,
∴∠ACE=∠D,
∵∠A=∠1,
∴180°?∠ACE?∠A=180°?∠D?∠1,
∵∠E=180°?∠ACE?∠A,∠F=180°?∠D?∠1,
∴∠E=∠F.
【解析】利用平行线的性质,易证∠ACE=∠D,再由∠A=∠1,利用三角形内角和定理,可证得结论。
17.【答案】 解:利用图形平移的性质及连接两点的线中,线段最短,可知:
.
而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
【解析】设B、D、E三点要使BD+DE最小,则三点在同一直线上即可.
一、单选题
1.下列图形中,不能由“基本图案”(小四边形)经过平移得到的图形为(?? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?
2.下列四幅图案中,能通过平移图得到的是(? )
A.??????????????????B.??????????????????C.??????????????????D.?
3.如图,将△ABE向右平移50px得到△DCF,如果△ABE的周长是400px(1px=0.04cm),那么四边形ABFD的周长是(?? )
A.?16cm??????????????????????????????????B.?18cm??????????????????????????????????C.?20cm??????????????????????????????????D.?21cm
4.如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )
?
A.?BE=4???????????????????????????????B.?∠F=30°???????????????????????????????C.?AB∥DE???????????????????????????????D.?DF=5
5.下列现象属于数学中的平移的是(?? )
A.?树叶从树上随风飘落???????????????????????????????????????????B.?升降电梯由一楼升到顶楼
C.?汽车方向盘的转动??????????????????????????????????????????????D.?“神舟”号卫星绕地球运动
6.如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2m , 则两条小路的总面积是( )m2
A.?108???????????????????????????????????????B.?104???????????????????????????????????????C.?100???????????????????????????????????????D.?98
7.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是(??? )
A.?先向下平移3格,再向右平移2格?????????????????????????B.?先向下平移3格,再向右平移1格
C.?先向下平移2格,再向右平移1格?????????????????????????D.?先向下平移2格,再向右平移2格
8.如图所示,由△ABC平移得到的三角形的个数是(? ????)
A.?5???????????????????????????????????????????B.?15???????????????????????????????????????????C.?8???????????????????????????????????????????D.?6
9.如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn?nDn(n>2),若ABn的长度为2018,则n的值为(?? )
A.?334??????????????????????????????????????B.?335??????????????????????????????????????C.?336??????????????????????????????????????D.?337
二、填空题
10.如图3,在方格中画着两艘完全一样的小船,左边小船向右平移了________格可以来到右边小船位置.
11.如图,已知在△ 中, ;将△ 沿边 所在的直线平移至△ (见图);若 ,则 ________cm.
12.如图所示,在长为 ,宽为 的草坪上修了一条宽恒为 宽的弯曲小路,则余下草坪的面积为________ .
13.如图,直角△ABC的周长为38,在其内部有6个小直角三角形,则这六个小直角三角形的周长的和为________.
14.如图是用三角尺和直尺画平行线的示意图,将三角尺 沿着直尺 平移到三角尺 的位置,就可以画出 的平行线 .若 , ,则直线 平移的距离为________cm.
三、解答题
15.如图,平面直角坐标系中,三角形 的顶点都在网格点上,平移三角形 ,使点 与坐标原点 重合,请写出图中点 的坐标并画出平移后的三角形
16.如图,点A、B、C、D在一条直线上,CE与BF交于点G , ∠A=∠1,CE∥DF , 求证:∠E=∠F
17.河的两岸成平行线,A,B是位于河两岸的两个车间(如图),要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法是:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB,EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.试说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
答案解析部分
一、单选题
1.【答案】 D
【解析】解:观察图象可知,选项A,B,C都是可以由基本图形平移得到,
选项D是旋转变换图形,不符合题意,
故答案为:D.
2.【答案】 B
【解析】解:平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移;
观察四个选项可知,只有选项B能通过平移图得到,
故答案为:B.
3.【答案】 C
【解析】∵1px?=?0.04cm,
∴50px=2cm,400px=16cm,
∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF
=AB+BE+AE+AD+EF
=△ABE的周长+AD+EF.
∵平移距离为2cm,
∴AD=EF=2cm,
∵△ABE的周长是16cm,
∴四边形ABFD的周长=16+2+2=20cm.
故答案为:C.
4.【答案】 D
【解析】解:∵把△ABC沿RS的方向平移到△DEF的位置,BC=5,∠A=80°,∠B=70°,
∴CF=BE=4,∠F=∠ACB=180°﹣∠A﹣∠B=180°﹣80°﹣70°=30°,AB∥DE,
∴A、B、C正确,D错误.
故答案为:D.
5.【答案】 B
【解析】A.树叶从树上随风飘落,不属于平移;
B.升降电梯由一楼升到顶楼属于平移;
C.汽车方向盘的转动属于旋转;
D. “神舟”号卫星绕地球运动属于旋转;
故答案为:B.
6.【答案】 C
【解析】解:利用平移可得,两条小路的总面积是:30×22﹣(30﹣2)(22﹣2)=100(m2).
故答案为:C .
7.【答案】 A
【解析】解:平移是先向下平移3格,再向右平移2格.
故答案为:A.
8.【答案】 A
【解析】△ABC经过平移后得到的三角形有一个顶角向下,图中这样的三角形有5个,即得A.
9.【答案】 B
【解析】∵AB=8,第1次平移将矩形ABCD沿AB的方向向右平移6个单位,得到矩形A1B1C1D1 ,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移6个单位,得到矩形A2B2C2D2…,
∴AA1=6,A1A2=6,A2B1=A1B1﹣A1A2=8﹣6=2,
∴AB1=AA1+A1A2+A2B1=6+6+2=14,
∴AB2的长为:6+6+8=20;
∵AB1=2×6+2=14,AB2=3×6+2=20,
∴ABn=(n+1)×6+2=2018,
解得:n=335.
故答案为:B.
10.【答案】 6
【解析】解:如图,
点A平移到点D,
∴左边小船向右平移了6格可以来到右边小船位置.
故答案为:6.
11.【答案】 3
【解析】∵将△ABC沿边BC所在的直线平移至△DEF,
∴BE=CF=BC?EC=5?2=3cm,
故答案为3.
12.【答案】 1200
【解析】长方形的长为50m,宽为(25-1).余下草坪的面积为:50×(25-1)=1200m2.
故答案为:1200.
13.【答案】 38
【解析】解:由平移的性质,6个小直角三角形较长的直角边平移后等于BC边,
较短的直角边平移后等于AC边,
斜边之和等于AB边长,
所以,6个小直角三角形的周长之和=Rt△ACB的周长,
∵直角三角形ACB的周长为38,
∴这6个小直角三角形的周长之和=38.
故答案为:38.
14.【答案】 5.5
【解析】解:AC+A′C′=AC′-A′C=9-2=7(cm),
A′C′=7÷2=3.5(cm),
CC′=A′C+A′C′=2+3.5=5.5(cm).
故直线AB平移的距离为5.5cm.
故答案为:5.5.
三、解答题
15.【答案】 解:(1)A(2,-1),B(4,3),C(1,2)(2)三角形A1OC1为所求。
画图注意:在坐标系中画对一个点给一分
要在坐标系中标出A1 , C1 , 不标的扣一分。
【解析】(1)根据点在坐标系里的位置,写出点的坐标,即可;
(2)由点B平移后与坐标原点O重合,可知,三角形先向左平移4个单位,再向下平移3个单位得到新的三角形.
16.【答案】 证明:∵CE∥DF,
∴∠ACE=∠D,
∵∠A=∠1,
∴180°?∠ACE?∠A=180°?∠D?∠1,
∵∠E=180°?∠ACE?∠A,∠F=180°?∠D?∠1,
∴∠E=∠F.
【解析】利用平行线的性质,易证∠ACE=∠D,再由∠A=∠1,利用三角形内角和定理,可证得结论。
17.【答案】 解:利用图形平移的性质及连接两点的线中,线段最短,可知:
.
而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
【解析】设B、D、E三点要使BD+DE最小,则三点在同一直线上即可.
