2.3.2 平行线的性质(共20张PPT)
文档属性
| 名称 | 2.3.2 平行线的性质(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 08:08:46 | ||
图片预览








文档简介
2.3.2平行线的性质
第二章
相交线与平行线
2020-2021北师大版七年级数学下册
1.掌握平行线的判定与平行线的性质的区别,(重点)
2.灵活地综合利用平行线的判定和性质解决实际问题。(难点)
学习目标
文字叙述
符号语言
图形
相等
两直线平行
∴a∥b
相等
两直线平行
∵
∴a∥b
互补
两直线平行
∴a∥b
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
新课导入
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
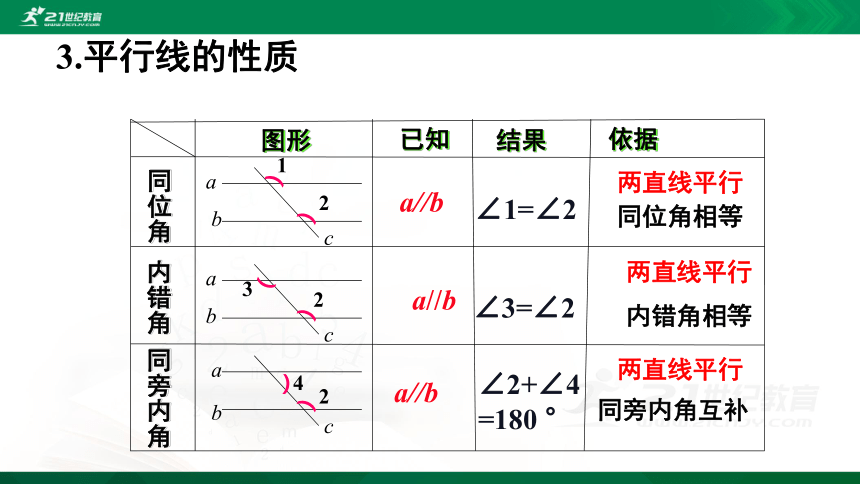
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
一,平行线性质与判定的综合运用
例1 根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据
是什么?
解:(1)∠1与∠2是内错角,
若∠1=∠2,则根据“内错角相等,两直线平行”,可得EF∥CE;
探究新知
(2)若∠2=∠M,可以判定哪两条直线平行?根据
是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
(2)∠2与∠M是同位角,若
∠2=∠M,则根据“同位角相等,两直线平行”,可得AM∥BF;
(3)∠2与∠3是同旁内角,若∠2+∠3=180°,则根据“同旁内角互补,两直线平行”,
可得AC∥MD.
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB
平行吗?说说你的理由.
解:因为∠1= ∠2,
根据“内错角相等,两直线
平行” ,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
解:因为a∥b,
根据“两直线平行,内错角
相等”.
所以∠2=∠1=107°.
因为c∥d,
根据“两直线平行,同旁内角互补”,
所以∠1+∠3=180°,
所以∠3= 180°-∠1=180°-107°=73°.
1.如图,已知直线a∥b,
直线c与a,b分别交于A,B,且∠1=120°,
则∠2=( )
(A)60° (B)120°
(C)30° (D)150°
【解析】选B.因为a∥b,所以∠1=∠3,
又∠2=∠3,所以∠2=120°.故选B.
课堂练习
2.如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
(A)40° (B)50°
(C)60° (D)140°
【解析】选B.因为AB∥CD,所以∠1=∠BCD,又因为∠1=40°,所以∠BCD=40°,因为DB⊥BC,
所以∠CBD=90°,所以∠2=180°-90°-40°=50°.
故选B.
3.如图,已知AB∥CD,∠A=70°,则∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
【解析】选C.因为AB∥CD,∠A=70°,所以∠1的邻补角为70°,所以∠1=110°.
4.如图,已知a∥b,∠1=65°,
则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
【解析】选C.因为a∥b,所以∠1=∠3=65°,所以∠2=180°-65°=115°.
5.如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠AEF,∠1=40°,
则∠2的度数为________.
【解析】因为EG平分∠AEF,所以∠AEG=∠GEF,
因为AB∥CD,
所以∠AEG=∠1=40°,
所以∠AEF=2∠AEG=80°,
所以∠2=180°-∠AEF=180°-80°=100°.
答案:100°
6. 已知∠3=45 °,∠1与∠2互余,试说明AB//CD.
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
7. 如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
8.如图所示,小张从家(图中A处)出发,
向南偏东40°的方向走到学校(图中B
处),再从学校出发,向北偏西75°的
方向走到小明家(图中C处),试问∠ABC
为多少度?
解:由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.
平行线的判定
平行线的性质
条件
结论
条件
结论
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
同位角相等
内错角相等
同旁内角互补
注意判定和性质二者之间的区别
课堂小结
谢谢聆听
第二章
相交线与平行线
2020-2021北师大版七年级数学下册
1.掌握平行线的判定与平行线的性质的区别,(重点)
2.灵活地综合利用平行线的判定和性质解决实际问题。(难点)
学习目标
文字叙述
符号语言
图形
相等
两直线平行
∴a∥b
相等
两直线平行
∵
∴a∥b
互补
两直线平行
∴a∥b
同位角
内错角
同旁内角
∵∠1=∠2
∠3=∠2
∵∠2+∠4=180°
a
b
c
1
2
3
4
1.平行线的判定
新课导入
方法4:如图1,若a∥b,b∥c,则a∥c.
( )
方法5:如图2,若a⊥b,a⊥c,则b∥c.
( )
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
a
b
c
图1
a
b
c
图2
图形
已知
结果
依据
同位角
内错角
同旁内角
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
同旁内角互补
a//b
两直线平行
3.平行线的性质
∠1=∠2
∠3=∠2
∠2+∠4
=180 °
一,平行线性质与判定的综合运用
例1 根据如图所示回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据
是什么?
解:(1)∠1与∠2是内错角,
若∠1=∠2,则根据“内错角相等,两直线平行”,可得EF∥CE;
探究新知
(2)若∠2=∠M,可以判定哪两条直线平行?根据
是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平
行?根据是什么?
(2)∠2与∠M是同位角,若
∠2=∠M,则根据“同位角相等,两直线平行”,可得AM∥BF;
(3)∠2与∠3是同旁内角,若∠2+∠3=180°,则根据“同旁内角互补,两直线平行”,
可得AC∥MD.
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB
平行吗?说说你的理由.
解:因为∠1= ∠2,
根据“内错角相等,两直线
平行” ,
所以EF∥CD.
又因为AB∥CD,
根据“平行于同一条直线的两条直线平行”,
所以EF∥AB.
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,
求∠2,∠3的度数.
解:因为a∥b,
根据“两直线平行,内错角
相等”.
所以∠2=∠1=107°.
因为c∥d,
根据“两直线平行,同旁内角互补”,
所以∠1+∠3=180°,
所以∠3= 180°-∠1=180°-107°=73°.
1.如图,已知直线a∥b,
直线c与a,b分别交于A,B,且∠1=120°,
则∠2=( )
(A)60° (B)120°
(C)30° (D)150°
【解析】选B.因为a∥b,所以∠1=∠3,
又∠2=∠3,所以∠2=120°.故选B.
课堂练习
2.如图,AB∥CD,DB⊥BC,∠1=40°,则∠2的度数是( )
(A)40° (B)50°
(C)60° (D)140°
【解析】选B.因为AB∥CD,所以∠1=∠BCD,又因为∠1=40°,所以∠BCD=40°,因为DB⊥BC,
所以∠CBD=90°,所以∠2=180°-90°-40°=50°.
故选B.
3.如图,已知AB∥CD,∠A=70°,则∠1的度数是( )
(A)70° (B)100°
(C)110° (D)130°
【解析】选C.因为AB∥CD,∠A=70°,所以∠1的邻补角为70°,所以∠1=110°.
4.如图,已知a∥b,∠1=65°,
则∠2的度数为( )
(A)65° (B)125°
(C)115° (D)25°
【解析】选C.因为a∥b,所以∠1=∠3=65°,所以∠2=180°-65°=115°.
5.如图,AB∥CD,直线EF分别交AB,CD
于点E,F,EG平分∠AEF,∠1=40°,
则∠2的度数为________.
【解析】因为EG平分∠AEF,所以∠AEG=∠GEF,
因为AB∥CD,
所以∠AEG=∠1=40°,
所以∠AEF=2∠AEG=80°,
所以∠2=180°-∠AEF=180°-80°=100°.
答案:100°
6. 已知∠3=45 °,∠1与∠2互余,试说明AB//CD.
解:由于∠1与∠2是对顶角,
∴∠1=∠2.
又∵∠1+∠2=90°(已知),
∴∠1=∠2=45°.
∵ ∠3=45°(已知),
∴∠ 2=∠3.
∴ AB∥CD(内错角相等,两直线平行).
1
2
3
A
B
C
D
7. 如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC的度数.
E
A
B
C
D
2
1
CD
EF
1
2
1
2
80
80
70
70
150
F
解:过点E作EF//AB.
∵AB//CD,EF//AB(已知),
∴ // (平行于同一直线的两直线平行).
∴∠A+∠ =180o,∠C+∠ =180o(两直线平行,同旁内角互补).
又∵∠A=100°,∠C=110°(已知),
∴∠ = °, ∠ = °(等量代换).
∴∠AEC=∠1+∠2= °+ ° = °.
8.如图所示,小张从家(图中A处)出发,
向南偏东40°的方向走到学校(图中B
处),再从学校出发,向北偏西75°的
方向走到小明家(图中C处),试问∠ABC
为多少度?
解:由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.
平行线的判定
平行线的性质
条件
结论
条件
结论
两直线平行
两直线平行
同位角相等
内错角相等
同旁内角互补
同位角相等
内错角相等
同旁内角互补
注意判定和性质二者之间的区别
课堂小结
谢谢聆听
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
