2020-2021学年苏科新版八年级下册数学《第9章 中心对称图形——平行四边形》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年苏科新版八年级下册数学《第9章 中心对称图形——平行四边形》单元测试卷(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 176.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-06 21:55:03 | ||
图片预览


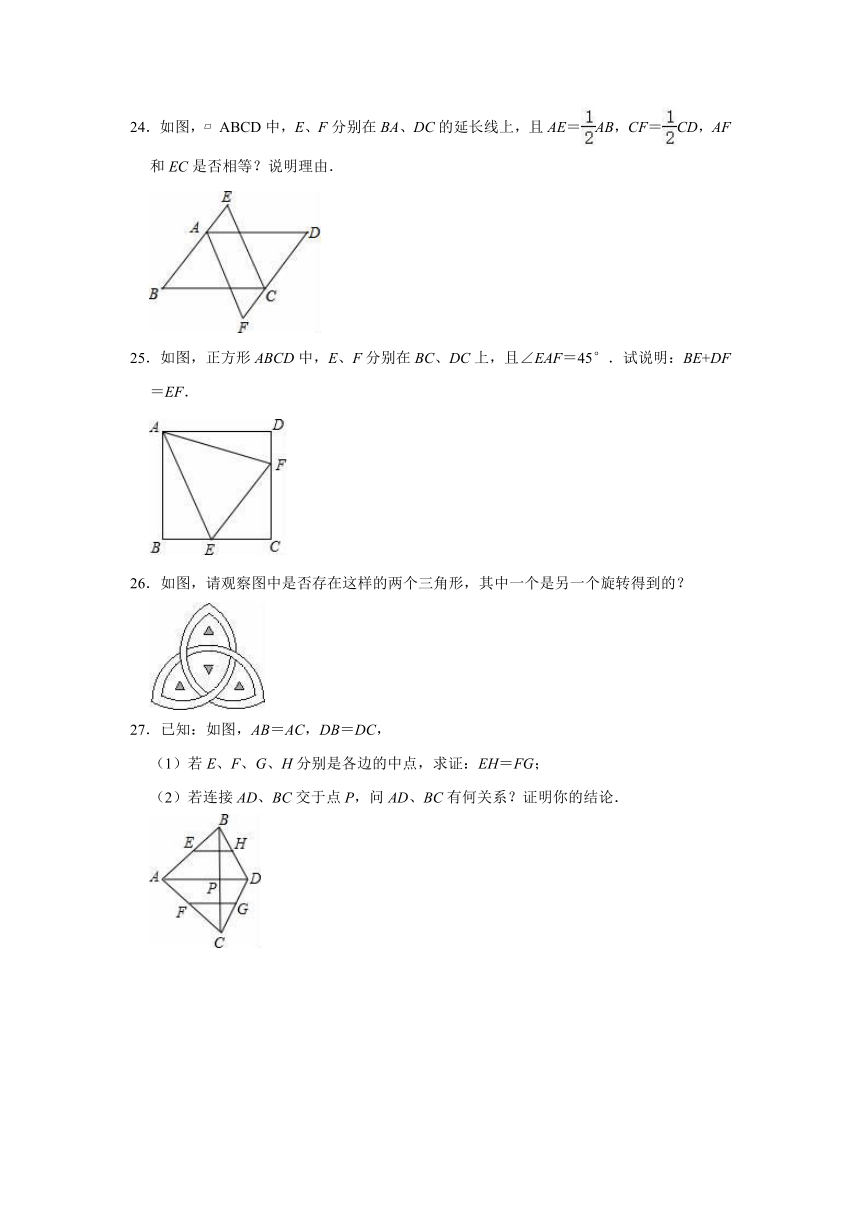

文档简介
2020-2021学年苏科新版八年级下册数学《第9章
中心对称图形——平行四边形》单元测试卷
一.选择题
1.如图,在△ABC中,∠CAB=70°,以顶点A为旋转中心,将△ABD旋转到△ACP的位置,则旋转角等于( )
A.70°
B.80°
C.60°
D.50°
2.以下不是旋转对称图形的是( )
A.
B.
C.
D.
3.经过矩形对称中心的任意一条直线,把这个矩形分成两部分,设这两部分的面积分别为S1和S2,则S1与S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
4.下列图形既是中心对称图形,又是轴对称图形的是( )
A.角
B.等边三角形
C.正十二边形
D.正以边形
5.已知?ABCD,添加下列一个条件:①AC⊥BD②∠BAD=90°
③AB=BC④AC=BD,其中能使?ABCD是菱形的为( )
A.①③
B.②③
C.③④
D.①②③
6.能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
7.若等边三角形的边长为4,则连接各边中点所成的三角形的周长是( )
A.4
B.6
C.8
D.1
8.以不共线的三点为平行四边形的其中三个顶点作平行四边形,一共可作平行四边形的个数是( )
A.2个
B.3个
C.4个
D.5个
9.下列图形中,某个图形中的一个矩形是另一个矩形顺时针方向旋转90°后形成的,这个图形是( )
A.
B.
C.
D.
10.有两个内角分别为90°,60°,30°的完全一样的三角形拼成四边形,其形状不同的有( )
A.2个
B.3个
C.4个
D.6个
二.填空题
11.?ABCD的周长为20cm,AB<AD,对角线AC,BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为
cm.
12.在线段、角、正方形、圆中,是轴对称图形但不是中心对称图形的是
.
13.根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是
.
14.用长度是40cm的绳子围成矩形,你认为能围成矩形的最大面积为
cm2.
15.已知:如图,AB∥CD,线段AC和BD交于点O,要使四边形ABCD是平行四边形,还需要增加的一个条件是:
(填一个即可)你判断的理由是:
.
16.要说明命题“若ab=0,则a+b=0”是假命题,可举反例
.
17.如图,在△ABC中,∠C=2∠B,D是BC上一点,AD⊥AB,点E是BD的中点.AC=6.5,AD=5,则AE=
,AB=
.
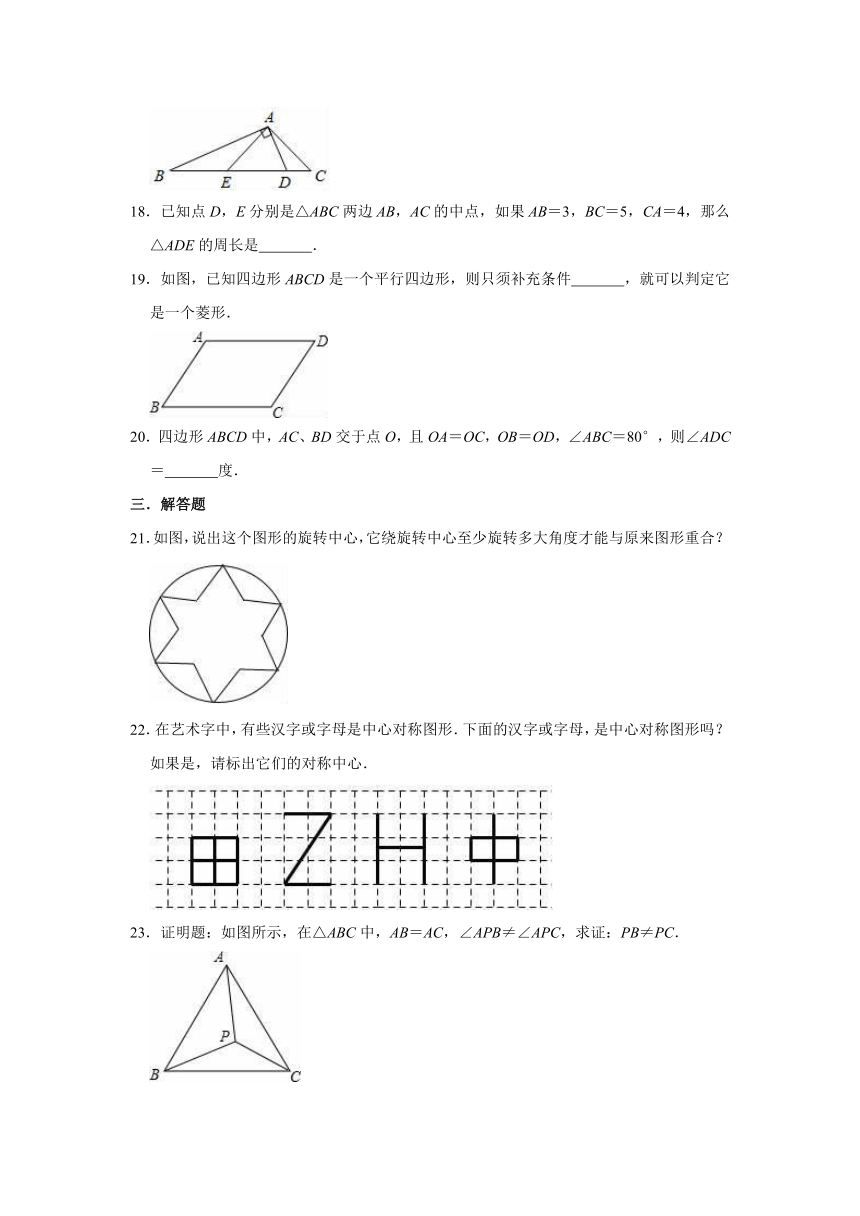
18.已知点D,E分别是△ABC两边AB,AC的中点,如果AB=3,BC=5,CA=4,那么△ADE的周长是
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.四边形ABCD中,AC、BD交于点O,且OA=OC,OB=OD,∠ABC=80°,则∠ADC=
度.
三.解答题
21.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?
22.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
23.证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC.
24.如图,?ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,AF和EC是否相等?说明理由.
25.如图,正方形ABCD中,E、F分别在BC、DC上,且∠EAF=45°.试说明:BE+DF=EF.
26.如图,请观察图中是否存在这样的两个三角形,其中一个是另一个旋转得到的?
27.已知:如图,AB=AC,DB=DC,
(1)若E、F、G、H分别是各边的中点,求证:EH=FG;
(2)若连接AD、BC交于点P,问AD、BC有何关系?证明你的结论.
参考答案与试题解析
一.选择题
1.解:∵△ABD旋转到△ACP的位置,
∴∠CAB为旋转角,
∵∠CAB=70°,
∴旋转角等于70°.
故选:A.
2.解:A、B、C是旋转对称图形;
D、不是旋转对称图形.
故选:D.
3.解:矩形ABCD中,AD=BC,
AO=BO=CO=DO,
∴△AOD≌△BOC(SSS),
∵∠ECO=∠FAO,OA=OC,∠EOC=∠FOA,
∴△OEC≌△OFA,
同理可证,△DEO≌△BFO,
∴S1=S2.
故选:C.
4.解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、不是中心对称图形,是轴对称图形,故本选项错误;
C、既是中心对称图形又是轴对称图形,故本选项正确.
D、不是中心对称图形,是轴对称图形,故本选项错误;
故选:C.
5.解:∵四边形ABCD是平行四边形,
①若AC⊥BD,则可得其为菱形,故①选项正确,
②中∠BAD=90°,得到一矩形,不是菱形,所以②错误,
③中一组邻边相等,也可得到一菱形,所以③成立,
④中并不能得到其为矩形,菱形或正方形等,所以④不成立,
故A选项中①③都正确,B中②不成立,C中④错误,而D中多一个选项②也不对,
则能使?ABCD是菱形的有①或③.
故选:A.
6.解:A中对边平行且相等,可得其为平行四边形,又对角线相等,可得其为矩形,A错;
B中只能判定是平行四边形,B错;
C中对角线平分且相等是平行四边形,再加上对角线互相垂直,即为正方形,C对;
D中是菱形,D错.
故选:C.
7.解:∵原等边三角形的边长=4,
∴原等边三角形的周长=3×4=12,
∴中点三角形的周长=×12=6.
故选:B.
8.解:如图以不共线的A、B、C三点,可做三个平行四边形:?ABCD、?ABFC、?AEBC.
故选:B.
9.解:根据题意,关键是找到:①定点﹣旋转中心;②旋转方向;③旋转角度;
分析可得:中的一个矩形是另一个矩形顺时针方向旋转90°后形成的;
故选:B.
10.解:根据平行四边形的基本性质:平行四边形的两组对角分别相等,可知角分别为,(1)90°,90°,90°90°;(2)120°,60°,120°,60°;(3)150°,30°,150°,30°;不是平行四边形的四边形为(4)60°,90°,120°,90°.共4种,
故选:C.
二.填空题
11.解:∵?ABCD的对角线AC,BD相交于点O,
∴O为BD的中点,
∵OE⊥BD,
∴BE=DE,
△ABE的周长=AB+AE+BE=AB+AD=×20=10(cm),
故答案为:10.
12.解:在线段、角、正方形、圆中,是轴对称图形但不是中心对称图形的是角.
故答案为:角.
13.解:∵矩形、菱形、正方形的对角线都具有平分的性质,
则根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是平分.
故答案为平分.
14.解:因为矩形周长为40cm,所以邻边和为20cm,若使面积最大,则只需两边长相等,即都为10cm,
所以最大面积为10×10=100cm2.
故答案为,100.
15.解:AD∥CB,
根据是:两组对边分别平行的四边形是平行四边形,
故答案为:AD∥CB,两组对边分别平行的四边形是平行四边形.
16.解:假设其为真命题,即ab=0,则a+b=0;
当a=0,b=1时,ab=0,但a+b=1≠0,
所以假设不成立,所以命题为假命题.
17.解:∵AD⊥AB,
∴△ABD为直角三角形,
又∵点E是BD的中点,
∴AE=BD=BE,
∴∠B=∠BAE,∠AEC=∠B+∠BAE=2∠B,
又∵∠C=2∠B,
∴∠AEC=∠C,
∴AE=AC=6.5,
Rt△ABD中,AD=5,BD=2AE=2×6.5=13,
∴AB==12,
故答案为:6.5;12.
18.解:∵点D,E分别是△ABC两边AB,AC的中点,
∴△ABC的周长是△ADE周长的2倍.
又∵AB=3,BC=5,CA=4,
∴△ADE的周长是(3+4+5)=6.
故答案为6.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
∴∠ADC=∠ABC=80°
故答案为:80.
三.解答题
21.解:这个图形的旋转中心为圆心;
∵360°÷6=60°,
∴该图形绕中心至少旋转60度后能和原来的图案互相重合.
22.解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
23.证明:假设PB≠PC不成立,则PB=PC;
∵在△ABP和△ACP中,
,
∴△ABP≌△ACP,
∴∠APB=∠APC;
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC.
24.解:AF=EC.
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
即AE∥CF,
∵AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF是平行四边形,
∴AF=EC.
25.证明:如图,把△ABE逆时针旋转90°得到△ADG,
∴BE=GD,AE=AG,
∵∠EAF=45°,
∴∠FAG=90°﹣45°=45°,
∴∠EAF=∠FAG,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=GF,
即EF=GD+DF,
∴BE+DF=EF.
26.解:仔细观察图形里面的三角形的大小和形状没有改变,因此存在这样两个三角形,其中一个是另一个旋转得到的.
故存在这样的两个三角形.
27.证明:(1)∵E、F、G、H分别是AB、AC、CD、DB的中点,
∴EH、FG为△ADB、△ADC的中位线.
∴EH=AD,FG=AD.
∴EH=FG.
(2)∵AB=AC,DB=DC,
∴AD垂直且平分BC.
中心对称图形——平行四边形》单元测试卷
一.选择题
1.如图,在△ABC中,∠CAB=70°,以顶点A为旋转中心,将△ABD旋转到△ACP的位置,则旋转角等于( )
A.70°
B.80°
C.60°
D.50°
2.以下不是旋转对称图形的是( )
A.
B.
C.
D.
3.经过矩形对称中心的任意一条直线,把这个矩形分成两部分,设这两部分的面积分别为S1和S2,则S1与S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.不能确定
4.下列图形既是中心对称图形,又是轴对称图形的是( )
A.角
B.等边三角形
C.正十二边形
D.正以边形
5.已知?ABCD,添加下列一个条件:①AC⊥BD②∠BAD=90°
③AB=BC④AC=BD,其中能使?ABCD是菱形的为( )
A.①③
B.②③
C.③④
D.①②③
6.能判别一个四边形是正方形的条件是( )
A.对角线相等,对边平行且相等
B.一组对边平行,一组对角相等
C.对角线互相垂直平分且相等
D.一组邻边相等,对角线互相平分
7.若等边三角形的边长为4,则连接各边中点所成的三角形的周长是( )
A.4
B.6
C.8
D.1
8.以不共线的三点为平行四边形的其中三个顶点作平行四边形,一共可作平行四边形的个数是( )
A.2个
B.3个
C.4个
D.5个
9.下列图形中,某个图形中的一个矩形是另一个矩形顺时针方向旋转90°后形成的,这个图形是( )
A.
B.
C.
D.
10.有两个内角分别为90°,60°,30°的完全一样的三角形拼成四边形,其形状不同的有( )
A.2个
B.3个
C.4个
D.6个
二.填空题
11.?ABCD的周长为20cm,AB<AD,对角线AC,BD相交于点O,OE⊥BD交AD于点E,则△ABE的周长为
cm.
12.在线段、角、正方形、圆中,是轴对称图形但不是中心对称图形的是
.
13.根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是
.
14.用长度是40cm的绳子围成矩形,你认为能围成矩形的最大面积为
cm2.
15.已知:如图,AB∥CD,线段AC和BD交于点O,要使四边形ABCD是平行四边形,还需要增加的一个条件是:
(填一个即可)你判断的理由是:
.
16.要说明命题“若ab=0,则a+b=0”是假命题,可举反例
.
17.如图,在△ABC中,∠C=2∠B,D是BC上一点,AD⊥AB,点E是BD的中点.AC=6.5,AD=5,则AE=
,AB=
.
18.已知点D,E分别是△ABC两边AB,AC的中点,如果AB=3,BC=5,CA=4,那么△ADE的周长是
.
19.如图,已知四边形ABCD是一个平行四边形,则只须补充条件
,就可以判定它是一个菱形.
20.四边形ABCD中,AC、BD交于点O,且OA=OC,OB=OD,∠ABC=80°,则∠ADC=
度.
三.解答题
21.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?
22.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.
23.证明题:如图所示,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC.
24.如图,?ABCD中,E、F分别在BA、DC的延长线上,且AE=AB,CF=CD,AF和EC是否相等?说明理由.
25.如图,正方形ABCD中,E、F分别在BC、DC上,且∠EAF=45°.试说明:BE+DF=EF.
26.如图,请观察图中是否存在这样的两个三角形,其中一个是另一个旋转得到的?
27.已知:如图,AB=AC,DB=DC,
(1)若E、F、G、H分别是各边的中点,求证:EH=FG;
(2)若连接AD、BC交于点P,问AD、BC有何关系?证明你的结论.
参考答案与试题解析
一.选择题
1.解:∵△ABD旋转到△ACP的位置,
∴∠CAB为旋转角,
∵∠CAB=70°,
∴旋转角等于70°.
故选:A.
2.解:A、B、C是旋转对称图形;
D、不是旋转对称图形.
故选:D.
3.解:矩形ABCD中,AD=BC,
AO=BO=CO=DO,
∴△AOD≌△BOC(SSS),
∵∠ECO=∠FAO,OA=OC,∠EOC=∠FOA,
∴△OEC≌△OFA,
同理可证,△DEO≌△BFO,
∴S1=S2.
故选:C.
4.解:A、是轴对称图形,不是中心对称图形,故本选项错误;
B、不是中心对称图形,是轴对称图形,故本选项错误;
C、既是中心对称图形又是轴对称图形,故本选项正确.
D、不是中心对称图形,是轴对称图形,故本选项错误;
故选:C.
5.解:∵四边形ABCD是平行四边形,
①若AC⊥BD,则可得其为菱形,故①选项正确,
②中∠BAD=90°,得到一矩形,不是菱形,所以②错误,
③中一组邻边相等,也可得到一菱形,所以③成立,
④中并不能得到其为矩形,菱形或正方形等,所以④不成立,
故A选项中①③都正确,B中②不成立,C中④错误,而D中多一个选项②也不对,
则能使?ABCD是菱形的有①或③.
故选:A.
6.解:A中对边平行且相等,可得其为平行四边形,又对角线相等,可得其为矩形,A错;
B中只能判定是平行四边形,B错;
C中对角线平分且相等是平行四边形,再加上对角线互相垂直,即为正方形,C对;
D中是菱形,D错.
故选:C.
7.解:∵原等边三角形的边长=4,
∴原等边三角形的周长=3×4=12,
∴中点三角形的周长=×12=6.
故选:B.
8.解:如图以不共线的A、B、C三点,可做三个平行四边形:?ABCD、?ABFC、?AEBC.
故选:B.
9.解:根据题意,关键是找到:①定点﹣旋转中心;②旋转方向;③旋转角度;
分析可得:中的一个矩形是另一个矩形顺时针方向旋转90°后形成的;
故选:B.
10.解:根据平行四边形的基本性质:平行四边形的两组对角分别相等,可知角分别为,(1)90°,90°,90°90°;(2)120°,60°,120°,60°;(3)150°,30°,150°,30°;不是平行四边形的四边形为(4)60°,90°,120°,90°.共4种,
故选:C.
二.填空题
11.解:∵?ABCD的对角线AC,BD相交于点O,
∴O为BD的中点,
∵OE⊥BD,
∴BE=DE,
△ABE的周长=AB+AE+BE=AB+AD=×20=10(cm),
故答案为:10.
12.解:在线段、角、正方形、圆中,是轴对称图形但不是中心对称图形的是角.
故答案为:角.
13.解:∵矩形、菱形、正方形的对角线都具有平分的性质,
则根据两条对角线的关系判断一个四边形是矩形或菱形或正方形的必不可少的条件是平分.
故答案为平分.
14.解:因为矩形周长为40cm,所以邻边和为20cm,若使面积最大,则只需两边长相等,即都为10cm,
所以最大面积为10×10=100cm2.
故答案为,100.
15.解:AD∥CB,
根据是:两组对边分别平行的四边形是平行四边形,
故答案为:AD∥CB,两组对边分别平行的四边形是平行四边形.
16.解:假设其为真命题,即ab=0,则a+b=0;
当a=0,b=1时,ab=0,但a+b=1≠0,
所以假设不成立,所以命题为假命题.
17.解:∵AD⊥AB,
∴△ABD为直角三角形,
又∵点E是BD的中点,
∴AE=BD=BE,
∴∠B=∠BAE,∠AEC=∠B+∠BAE=2∠B,
又∵∠C=2∠B,
∴∠AEC=∠C,
∴AE=AC=6.5,
Rt△ABD中,AD=5,BD=2AE=2×6.5=13,
∴AB==12,
故答案为:6.5;12.
18.解:∵点D,E分别是△ABC两边AB,AC的中点,
∴△ABC的周长是△ADE周长的2倍.
又∵AB=3,BC=5,CA=4,
∴△ADE的周长是(3+4+5)=6.
故答案为6.
19.解:补充的条件是AB=BC,
理由是:∵AB=BC,四边形ABCD是平行四边形,
∴平行四边形ABCD是菱形,
故答案为:AB=BC.
20.解:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
∴∠ADC=∠ABC=80°
故答案为:80.
三.解答题
21.解:这个图形的旋转中心为圆心;
∵360°÷6=60°,
∴该图形绕中心至少旋转60度后能和原来的图案互相重合.
22.解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.
23.证明:假设PB≠PC不成立,则PB=PC;
∵在△ABP和△ACP中,
,
∴△ABP≌△ACP,
∴∠APB=∠APC;
与∠APB≠∠APC相矛盾.因而PB=PC不成立,则PB≠PC.
24.解:AF=EC.
理由:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
即AE∥CF,
∵AE=AB,CF=CD,
∴AE=CF,
∴四边形AECF是平行四边形,
∴AF=EC.
25.证明:如图,把△ABE逆时针旋转90°得到△ADG,
∴BE=GD,AE=AG,
∵∠EAF=45°,
∴∠FAG=90°﹣45°=45°,
∴∠EAF=∠FAG,
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=GF,
即EF=GD+DF,
∴BE+DF=EF.
26.解:仔细观察图形里面的三角形的大小和形状没有改变,因此存在这样两个三角形,其中一个是另一个旋转得到的.
故存在这样的两个三角形.
27.证明:(1)∵E、F、G、H分别是AB、AC、CD、DB的中点,
∴EH、FG为△ADB、△ADC的中位线.
∴EH=AD,FG=AD.
∴EH=FG.
(2)∵AB=AC,DB=DC,
∴AD垂直且平分BC.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
