11.3.2 直线与平面平行同步作业2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.3.2 直线与平面平行同步作业2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | docx | ||
| 文件大小 | 730.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 22:47:31 | ||
图片预览



文档简介
11.3.2 直线与平面平行
1.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α.以其中两个为条件,余下的一个为结论,可构成三个命题:①②?③,②③?①,①③?②,其中正确命题的个数为( )
A.0
B.1
C.2
D.3
2.在正方体ABCD-A'B'C'D'中,点E,F分别为平面ABCD和平面A'B'C'D'的中心,则正方体的六个面中与EF平行的平面有( )
A.1个
B.2个
C.3个
D.4个
3.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )
A.0
B.1
C.2
D.3
4.
(多选题)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
5.如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
6.下列两个命题,在“ ”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为直线,α为平面),则此条件为 .①?l∥α;②?l∥α.?
7.
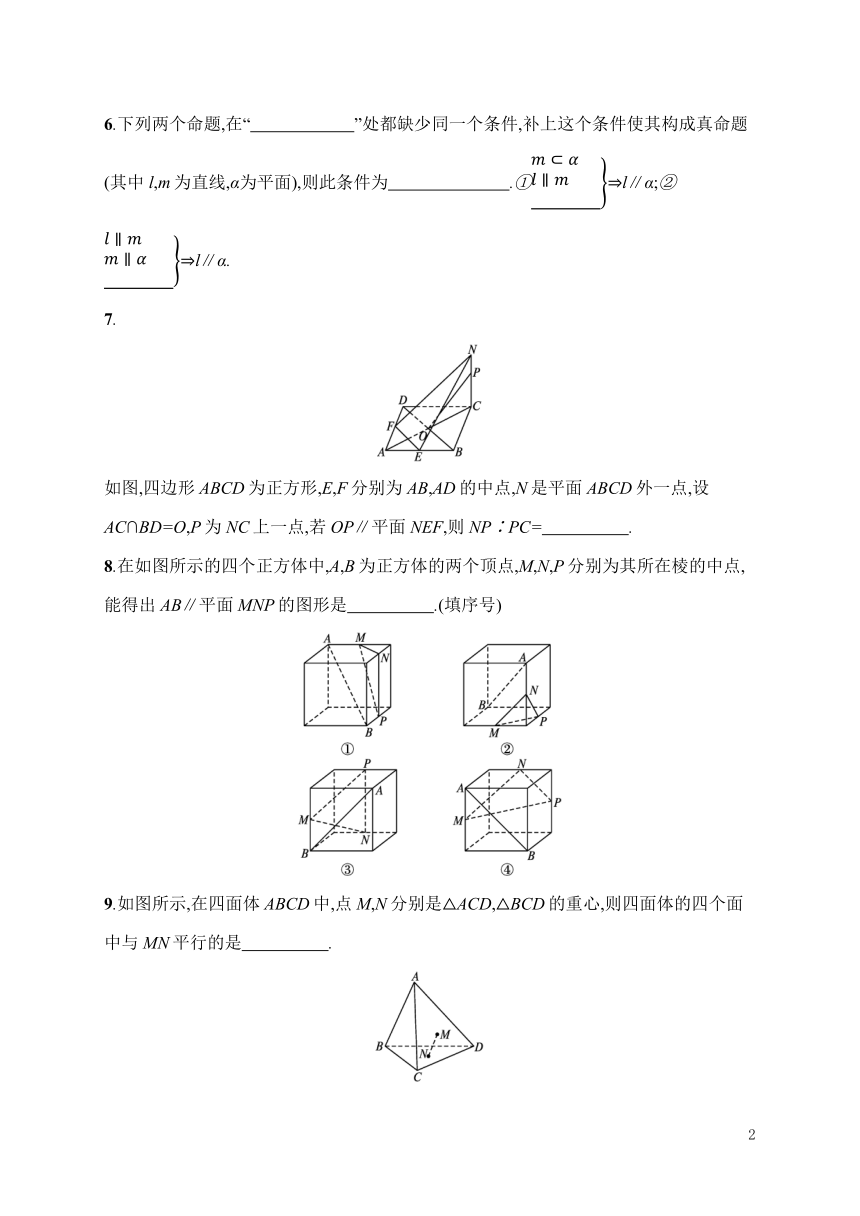
如图,四边形ABCD为正方形,E,F分别为AB,AD的中点,N是平面ABCD外一点,设AC∩BD=O,P为NC上一点,若OP∥平面NEF,则NP∶PC= .?
8.在如图所示的四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是 .(填序号)?
9.如图所示,在四面体ABCD中,点M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是 .?
10.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,E,E1分别是棱AD,AA1的中点,设F是棱AB的中点,证明:直线EE1∥平面FCC1.
素养提升
1.有下列四个条件:①a?β,b?β,a∥b;②b?β,a∥b;③a∥b∥c,b?β,c?β;④a,b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①②
B.①③
C.①④
D.②④
2.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
3.在空间四边形ABCD中,E,F分别是边AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行
B.相交
C.在平面内
D.异面
4.有一正方体木块如图所示,点P在平面A'B'C'D'内,棱BC平行于平面A'B'C'D',要经过P和棱BC将木块锯开,锯开的面必须平整,有N种锯法,则N为( )
A.0
B.1
C.2
D.无数
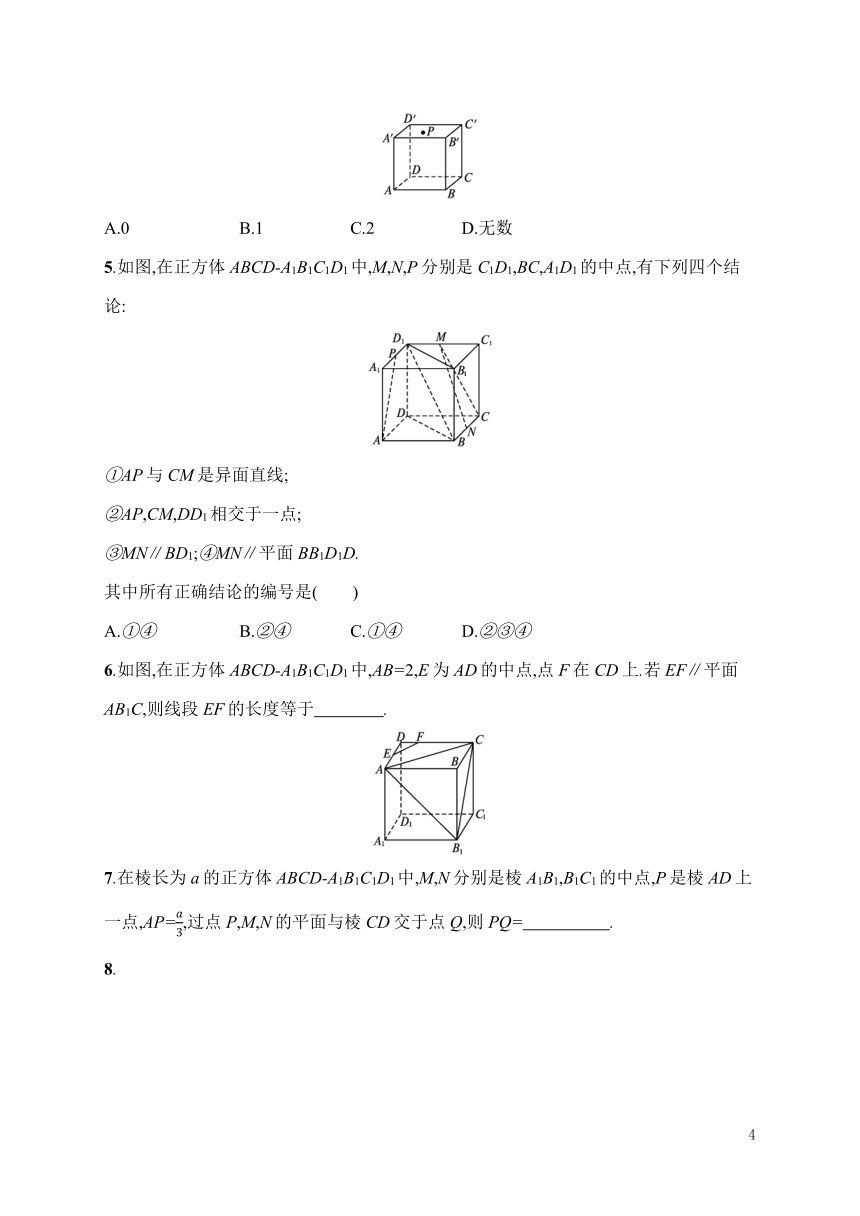
5.如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;
②AP,CM,DD1相交于一点;
③MN∥BD1;④MN∥平面BB1D1D.
其中所有正确结论的编号是( )
A.①④
B.②④
C.①④
D.②③④
6.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于 .?
7.在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上一点,AP=,过点P,M,N的平面与棱CD交于点Q,则PQ= .?
8.
如图,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件 时,就有MN∥平面B1BDD1,其中N是BC的中点.(填上一个正确的条件即可,不必考虑全部可能的情况)?
9.如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
答案
1.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α.以其中两个为条件,余下的一个为结论,可构成三个命题:①②?③,②③?①,①③?②,其中正确命题的个数为( )
A.0
B.1
C.2
D.3
答案C
解析本题考查线线平行与线面平行的判定和相互转化.m?α,n?α,m∥n,m∥α?n∥α,即①②?③;同理可得①③?②;由m∥α且n∥α,显然推不出m∥n,所以②③①.所以正确命题的个数为2,故选C.
2.在正方体ABCD-A'B'C'D'中,点E,F分别为平面ABCD和平面A'B'C'D'的中心,则正方体的六个面中与EF平行的平面有( )
A.1个
B.2个
C.3个
D.4个
答案D
解析如图正方体四个侧面AA'B'B,BB'C'C,CC'D'D,DD'A'A都与EF平行.故选D.
3.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )
A.0
B.1
C.2
D.3
答案C
解析如图,由线面平行的判定定理可知BD∥平面EFGH,AC∥平面EFGH.故选C.
4.
(多选题)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
答案ABC
解析由题意知,OM是△BPD的中位线,
∴OM∥PD,故A正确;PD?平面PCD,OM?平面PCD,
∴OM∥平面PCD,故B正确;同理,可得OM∥平面PDA,故C正确;OM与平面PBA和平面PBC都相交,故D不正确.
5.如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
答案A
解析由长方体性质知,EF∥平面ABCD,
∵EF?平面EFGH,平面EFGH∩平面ABCD=GH,∴EF∥GH,又EF∥AB,∴GH∥AB.故选A.
6.下列两个命题,在“ ”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为直线,α为平面),则此条件为 .①?l∥α;②?l∥α.?
答案l?α
解析①由线面平行的判定定理知应填“l?α”;②易知应填“l?α”.
7.
如图,四边形ABCD为正方形,E,F分别为AB,AD的中点,N是平面ABCD外一点,设AC∩BD=O,P为NC上一点,若OP∥平面NEF,则NP∶PC= .?
答案1∶2
解析设AC∩EF=H,连接NH.
因为OP∥平面NEF,平面NEF∩平面NHC=NH,
所以OP∥NH,
所以NP∶PC=HO∶OC.
在正方形ABCD中,因为E,F分别为AB,AD的中点,所以HO∶OC=1∶2.所以NP∶PC=1∶2.
8.在如图所示的四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是 .(填序号)?
答案①④
解析本题考查空间直线与平面平行的判定.①中,记点B正上方的顶点为C,连接AC,图略,则易证平面ABC∥平面MNP,所以AB∥平面MNP;④中AB∥NP,根据空间直线与平面平行的判定定理可以得出AB∥平面MNP;②③中,AB均与平面MNP相交.
9.如图所示,在四面体ABCD中,点M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是 .?
答案平面ABC、平面ABD
解析连接AM并延长,交CD于点E,连接BN,并延长交CD于点F,图略,由重心性质可知,E,F重合为一点,且该点为CD的中点E,由,得MN∥AB.因此,MN∥平面ABC且MN∥平面ABD.
10.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,E,E1分别是棱AD,AA1的中点,设F是棱AB的中点,证明:直线EE1∥平面FCC1.
证明如图,取A1B1的中点为F1.连接FF1,C1F1.
由于FF1∥BB1∥CC1,
所以F1∈平面FCC1.
因此平面FCC1即为平面C1CFF1.
连接A1D,F1C,由于A1F1?D1C1?DC,
所以四边形A1DCF1为平行四边形,
因此,A1D∥F1C.
又EE1∥A1D,得EE1∥F1C.
而EE1?平面FCC1,F1C?平面FCC1.
故EE1∥平面FCC1.
素养提升
1.有下列四个条件:①a?β,b?β,a∥b;②b?β,a∥b;③a∥b∥c,b?β,c?β;④a,b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①②
B.①③
C.①④
D.②④
答案C
解析对于①,∵a?β,b?β,a∥b,由线面平行的判定定理可知直线a∥平面β;对于②,∵b?β,a∥b,则直线a∥平面β或直线a?平面β;对于③,∵a∥b∥c,b?β,c?β,则直线a∥平面β或直线a?平面β;对于④,∵a,b是异面直线,b?β,则a?β,∵a∥c,c?β,∴直线a∥平面β.
2.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
答案B
解析①直线不在平面内,可能直线与平面相交.有②正确.③中直线与某些直线异面.故选B.
3.在空间四边形ABCD中,E,F分别是边AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行
B.相交
C.在平面内
D.异面
答案A
解析如图,由,得AC∥EF.
又EF?平面DEF,AC?平面DEF,
∴AC∥平面DEF.故选A.
4.有一正方体木块如图所示,点P在平面A'B'C'D'内,棱BC平行于平面A'B'C'D',要经过P和棱BC将木块锯开,锯开的面必须平整,有N种锯法,则N为( )
A.0
B.1
C.2
D.无数
答案B
解析∵BC∥平面A'B'C'D',
∴BC∥B'C',
在平面A'C'上过点P作EF∥B'C',则EF∥BC,
∴沿EF,BC所确定的平面锯开即可.
又由于此平面唯一确定,∴只有一种方法,故选B.
5.如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;
②AP,CM,DD1相交于一点;
③MN∥BD1;④MN∥平面BB1D1D.
其中所有正确结论的编号是( )
A.①④
B.②④
C.①④
D.②③④
答案B
解析如图,连接MP.
∵MP∥AC,MP≠AC,
∴AP,CM是相交直线,设AP∩CM=G,则G∈平面ADD1A1,且G∈平面C1CDD1,又平面ADD1A1∩平面C1CDD1=DD1,∴AP,CM,DD1相交于一点,故①不正确,②正确;设AC∩BD=O,连接ON,OD1,则有ON?D1M,∴四边形ONMD1为平行四边形,则MN∥OD1,∴③不正确;
又MN?平面BB1D1D,OD1?平面BB1D1D,
∴MN∥平面BB1D1D,则④正确.
6.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于 .?
答案
解析∵EF∥平面AB1C,EF?平面AC,平面AB1C∩平面AC=AC,∴EF∥AC,又E为AD的中点,点F在CD上,∴F是CD的中点,∴EF=AC=.
7.在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上一点,AP=,过点P,M,N的平面与棱CD交于点Q,则PQ= .?
答案a
解析∵MN∥平面ABCD,平面PMN∩平面ABCD=PQ,MN?平面PMN,∴MN∥PQ.
易知DP=DQ=a,故PQ=a=a.
8.
如图,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件 时,就有MN∥平面B1BDD1,其中N是BC的中点.(填上一个正确的条件即可,不必考虑全部可能的情况)?
答案M与H重合(答案不唯一,又如M∈FH)
解析∵H,N分别是CD和CB的中点,连接HN,BD,图略,易知BD∥HN.
又BD?平面B1BDD1,HN?平面B1BDD1,
故HN∥平面B1BDD1,
故取M点与H点重合便符合题意.
9.如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
(1)证明因为BC∥AD,BC?平面PAD,AD?平面PAD,所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
(2)解平行.取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.
可知四边形AMNE为平行四边形.
所以MN∥AE.
又因为MN?平面APD,AE?平面APD,
所以MN∥平面APD.
2
1.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α.以其中两个为条件,余下的一个为结论,可构成三个命题:①②?③,②③?①,①③?②,其中正确命题的个数为( )
A.0
B.1
C.2
D.3
2.在正方体ABCD-A'B'C'D'中,点E,F分别为平面ABCD和平面A'B'C'D'的中心,则正方体的六个面中与EF平行的平面有( )
A.1个
B.2个
C.3个
D.4个
3.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )
A.0
B.1
C.2
D.3
4.
(多选题)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
5.如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
6.下列两个命题,在“ ”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为直线,α为平面),则此条件为 .①?l∥α;②?l∥α.?
7.
如图,四边形ABCD为正方形,E,F分别为AB,AD的中点,N是平面ABCD外一点,设AC∩BD=O,P为NC上一点,若OP∥平面NEF,则NP∶PC= .?
8.在如图所示的四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是 .(填序号)?
9.如图所示,在四面体ABCD中,点M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是 .?
10.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,E,E1分别是棱AD,AA1的中点,设F是棱AB的中点,证明:直线EE1∥平面FCC1.
素养提升
1.有下列四个条件:①a?β,b?β,a∥b;②b?β,a∥b;③a∥b∥c,b?β,c?β;④a,b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①②
B.①③
C.①④
D.②④
2.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
3.在空间四边形ABCD中,E,F分别是边AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行
B.相交
C.在平面内
D.异面
4.有一正方体木块如图所示,点P在平面A'B'C'D'内,棱BC平行于平面A'B'C'D',要经过P和棱BC将木块锯开,锯开的面必须平整,有N种锯法,则N为( )
A.0
B.1
C.2
D.无数
5.如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;
②AP,CM,DD1相交于一点;
③MN∥BD1;④MN∥平面BB1D1D.
其中所有正确结论的编号是( )
A.①④
B.②④
C.①④
D.②③④
6.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于 .?
7.在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上一点,AP=,过点P,M,N的平面与棱CD交于点Q,则PQ= .?
8.
如图,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件 时,就有MN∥平面B1BDD1,其中N是BC的中点.(填上一个正确的条件即可,不必考虑全部可能的情况)?
9.如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
答案
1.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α.以其中两个为条件,余下的一个为结论,可构成三个命题:①②?③,②③?①,①③?②,其中正确命题的个数为( )
A.0
B.1
C.2
D.3
答案C
解析本题考查线线平行与线面平行的判定和相互转化.m?α,n?α,m∥n,m∥α?n∥α,即①②?③;同理可得①③?②;由m∥α且n∥α,显然推不出m∥n,所以②③①.所以正确命题的个数为2,故选C.
2.在正方体ABCD-A'B'C'D'中,点E,F分别为平面ABCD和平面A'B'C'D'的中心,则正方体的六个面中与EF平行的平面有( )
A.1个
B.2个
C.3个
D.4个
答案D
解析如图正方体四个侧面AA'B'B,BB'C'C,CC'D'D,DD'A'A都与EF平行.故选D.
3.点E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )
A.0
B.1
C.2
D.3
答案C
解析如图,由线面平行的判定定理可知BD∥平面EFGH,AC∥平面EFGH.故选C.
4.
(多选题)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出以下结论,其中正确的是
( )
A.OM∥PD
B.OM∥平面PCD
C.OM∥平面PDA
D.OM∥平面PBA
答案ABC
解析由题意知,OM是△BPD的中位线,
∴OM∥PD,故A正确;PD?平面PCD,OM?平面PCD,
∴OM∥平面PCD,故B正确;同理,可得OM∥平面PDA,故C正确;OM与平面PBA和平面PBC都相交,故D不正确.
5.如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行
B.相交
C.异面
D.平行或异面
答案A
解析由长方体性质知,EF∥平面ABCD,
∵EF?平面EFGH,平面EFGH∩平面ABCD=GH,∴EF∥GH,又EF∥AB,∴GH∥AB.故选A.
6.下列两个命题,在“ ”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为直线,α为平面),则此条件为 .①?l∥α;②?l∥α.?
答案l?α
解析①由线面平行的判定定理知应填“l?α”;②易知应填“l?α”.
7.
如图,四边形ABCD为正方形,E,F分别为AB,AD的中点,N是平面ABCD外一点,设AC∩BD=O,P为NC上一点,若OP∥平面NEF,则NP∶PC= .?
答案1∶2
解析设AC∩EF=H,连接NH.
因为OP∥平面NEF,平面NEF∩平面NHC=NH,
所以OP∥NH,
所以NP∶PC=HO∶OC.
在正方形ABCD中,因为E,F分别为AB,AD的中点,所以HO∶OC=1∶2.所以NP∶PC=1∶2.
8.在如图所示的四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形是 .(填序号)?
答案①④
解析本题考查空间直线与平面平行的判定.①中,记点B正上方的顶点为C,连接AC,图略,则易证平面ABC∥平面MNP,所以AB∥平面MNP;④中AB∥NP,根据空间直线与平面平行的判定定理可以得出AB∥平面MNP;②③中,AB均与平面MNP相交.
9.如图所示,在四面体ABCD中,点M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是 .?
答案平面ABC、平面ABD
解析连接AM并延长,交CD于点E,连接BN,并延长交CD于点F,图略,由重心性质可知,E,F重合为一点,且该点为CD的中点E,由,得MN∥AB.因此,MN∥平面ABC且MN∥平面ABD.
10.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,E,E1分别是棱AD,AA1的中点,设F是棱AB的中点,证明:直线EE1∥平面FCC1.
证明如图,取A1B1的中点为F1.连接FF1,C1F1.
由于FF1∥BB1∥CC1,
所以F1∈平面FCC1.
因此平面FCC1即为平面C1CFF1.
连接A1D,F1C,由于A1F1?D1C1?DC,
所以四边形A1DCF1为平行四边形,
因此,A1D∥F1C.
又EE1∥A1D,得EE1∥F1C.
而EE1?平面FCC1,F1C?平面FCC1.
故EE1∥平面FCC1.
素养提升
1.有下列四个条件:①a?β,b?β,a∥b;②b?β,a∥b;③a∥b∥c,b?β,c?β;④a,b是异面直线,a∥c,b?β,c?β.其中能保证直线a∥平面β的条件是( )
A.①②
B.①③
C.①④
D.②④
答案C
解析对于①,∵a?β,b?β,a∥b,由线面平行的判定定理可知直线a∥平面β;对于②,∵b?β,a∥b,则直线a∥平面β或直线a?平面β;对于③,∵a∥b∥c,b?β,c?β,则直线a∥平面β或直线a?平面β;对于④,∵a,b是异面直线,b?β,则a?β,∵a∥c,c?β,∴直线a∥平面β.
2.下列命题:
①如果一条直线不在平面内,则这条直线就与这个平面平行;
②过直线外一点,可以作无数个平面与这条直线平行;
③如果一条直线与平面平行,则它与平面内的任何直线平行.
其中正确命题的个数为( )
A.0
B.1
C.2
D.3
答案B
解析①直线不在平面内,可能直线与平面相交.有②正确.③中直线与某些直线异面.故选B.
3.在空间四边形ABCD中,E,F分别是边AB和BC上的点,若AE∶EB=CF∶FB=1∶2,则对角线AC和平面DEF的位置关系是( )
A.平行
B.相交
C.在平面内
D.异面
答案A
解析如图,由,得AC∥EF.
又EF?平面DEF,AC?平面DEF,
∴AC∥平面DEF.故选A.
4.有一正方体木块如图所示,点P在平面A'B'C'D'内,棱BC平行于平面A'B'C'D',要经过P和棱BC将木块锯开,锯开的面必须平整,有N种锯法,则N为( )
A.0
B.1
C.2
D.无数
答案B
解析∵BC∥平面A'B'C'D',
∴BC∥B'C',
在平面A'C'上过点P作EF∥B'C',则EF∥BC,
∴沿EF,BC所确定的平面锯开即可.
又由于此平面唯一确定,∴只有一种方法,故选B.
5.如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;
②AP,CM,DD1相交于一点;
③MN∥BD1;④MN∥平面BB1D1D.
其中所有正确结论的编号是( )
A.①④
B.②④
C.①④
D.②③④
答案B
解析如图,连接MP.
∵MP∥AC,MP≠AC,
∴AP,CM是相交直线,设AP∩CM=G,则G∈平面ADD1A1,且G∈平面C1CDD1,又平面ADD1A1∩平面C1CDD1=DD1,∴AP,CM,DD1相交于一点,故①不正确,②正确;设AC∩BD=O,连接ON,OD1,则有ON?D1M,∴四边形ONMD1为平行四边形,则MN∥OD1,∴③不正确;
又MN?平面BB1D1D,OD1?平面BB1D1D,
∴MN∥平面BB1D1D,则④正确.
6.如图,在正方体ABCD-A1B1C1D1中,AB=2,E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度等于 .?
答案
解析∵EF∥平面AB1C,EF?平面AC,平面AB1C∩平面AC=AC,∴EF∥AC,又E为AD的中点,点F在CD上,∴F是CD的中点,∴EF=AC=.
7.在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱A1B1,B1C1的中点,P是棱AD上一点,AP=,过点P,M,N的平面与棱CD交于点Q,则PQ= .?
答案a
解析∵MN∥平面ABCD,平面PMN∩平面ABCD=PQ,MN?平面PMN,∴MN∥PQ.
易知DP=DQ=a,故PQ=a=a.
8.
如图,在正四棱柱ABCD-A1B1C1D1中,E,F,G,H分别是棱C1C,C1D1,D1D,DC的中点,点M在四边形EFGH及其内部运动,则M只需满足条件 时,就有MN∥平面B1BDD1,其中N是BC的中点.(填上一个正确的条件即可,不必考虑全部可能的情况)?
答案M与H重合(答案不唯一,又如M∈FH)
解析∵H,N分别是CD和CB的中点,连接HN,BD,图略,易知BD∥HN.
又BD?平面B1BDD1,HN?平面B1BDD1,
故HN∥平面B1BDD1,
故取M点与H点重合便符合题意.
9.如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)求证:l∥BC;
(2)MN与平面PAD是否平行?试证明你的结论.
(1)证明因为BC∥AD,BC?平面PAD,AD?平面PAD,所以BC∥平面PAD.
又因为平面PBC∩平面PAD=l,所以BC∥l.
(2)解平行.取PD的中点E,连接AE,NE,可以证得NE∥AM且NE=AM.
可知四边形AMNE为平行四边形.
所以MN∥AE.
又因为MN?平面APD,AE?平面APD,
所以MN∥平面APD.
2
