11.3.3 平面与平面平行同步作业2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.3.3 平面与平面平行同步作业2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | docx | ||
| 文件大小 | 652.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览



文档简介
11.3.3 平面与平面平行
1.(多选题)设α,β为两个不重合的平面,则下列条件能得到α∥β的是( )
A.α内有无数条直线与β平行
B.平面α,β平行于同一平面
C.平面α,β平行于同一条直线
D.α内有两条相交直线与β平行
2.(多选题)已知a,b表示两条不重合的直线,α,β,γ表示三个不重合的平面,给出下列命题,其中正确的是( )
A.若α∩γ=a,β∩γ=b,且a∥b,则α∥β
B.若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β
C.若a∥α,a∥β,则α∥β
D.若a?α,a∥β,α∩β=b,则a∥b
3.已知直线a,b,平面α,β,下列命题正确的是( )
A.若a∥α,b∥a,则b∥α
B.若a∥α,b∥α,a?β,b?β,则β∥α
C.若α∥β,b∥α,则b∥β
D.若α∥β,a?α,则a∥β
4.a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出六个命题:
①?a∥b;②?a∥b;③?α∥β;
④?α∥β;⑤?a∥α;⑥?a∥α.
其中正确的命题是( )
A.②③
B.①④⑤
C.①④
D.①③④
5.在正方体EFGH-E1F1G1H1中,四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
6.在正方体ABCD-A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E,F,则四边形D1EBF的形状是
( )
A.矩形
B.菱形
C.平行四边形
D.正方形
7.下列说法正确的是( )
A.平行于同一条直线的两个平面平行
B.平行于同一个平面的两个平面平行
C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行
D.若三条直线a,b,c两两平行,则在过直线a的平面中,有且只有一个平面与b,c均平行
8.过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是 .?
9.
如图,ABCD是空间四边形,E,F,G,H分别是其四边上的点且共面,AC∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,= .?
素养提升
1.已知a,b表示直线,α,β,γ表示平面,则下列推理正确的是( )
A.α∩β=a,b?α?a∥b
B.α∩β=a,a∥b?b∥α,且b∥β
C.a∥β,b∥β,a?α,b?α?α∥β
D.α∥β,α∩γ=a,β∩γ=b?a∥b
2.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当A,B分别在α,β内运动时,那么所有的动点C( )
A.不共面
B.当且仅当A,B在两条相交直线上移动时才共面
C.当且仅当A,B在两条给定的平行直线上移动时才共面
D.不论A,B如何移动都共面
3.
如图,在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上,平面AEF∥平面BD1G,则=( )
A.
B.
C.
D.
4.如图,P是△ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于点A',B',C',若,则=( )
A.
B.
C.
D.
5.
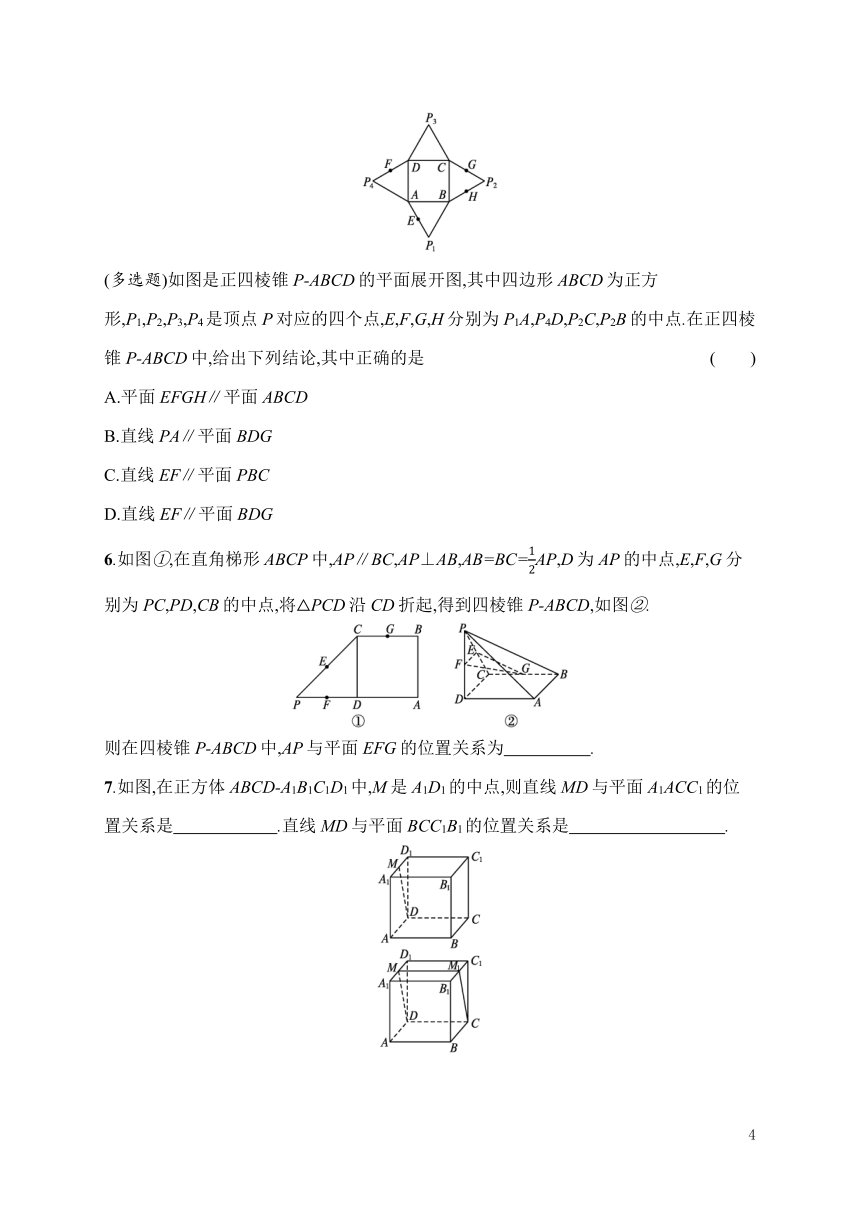
(多选题)如图是正四棱锥P-ABCD的平面展开图,其中四边形ABCD为正方形,P1,P2,P3,P4是顶点P对应的四个点,E,F,G,H分别为P1A,P4D,P2C,P2B的中点.在正四棱锥P-ABCD中,给出下列结论,其中正确的是
( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
6.如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.
则在四棱锥P-ABCD中,AP与平面EFG的位置关系为 .?
7.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线MD与平面A1ACC1的位置关系是 .直线MD与平面BCC1B1的位置关系是 .?
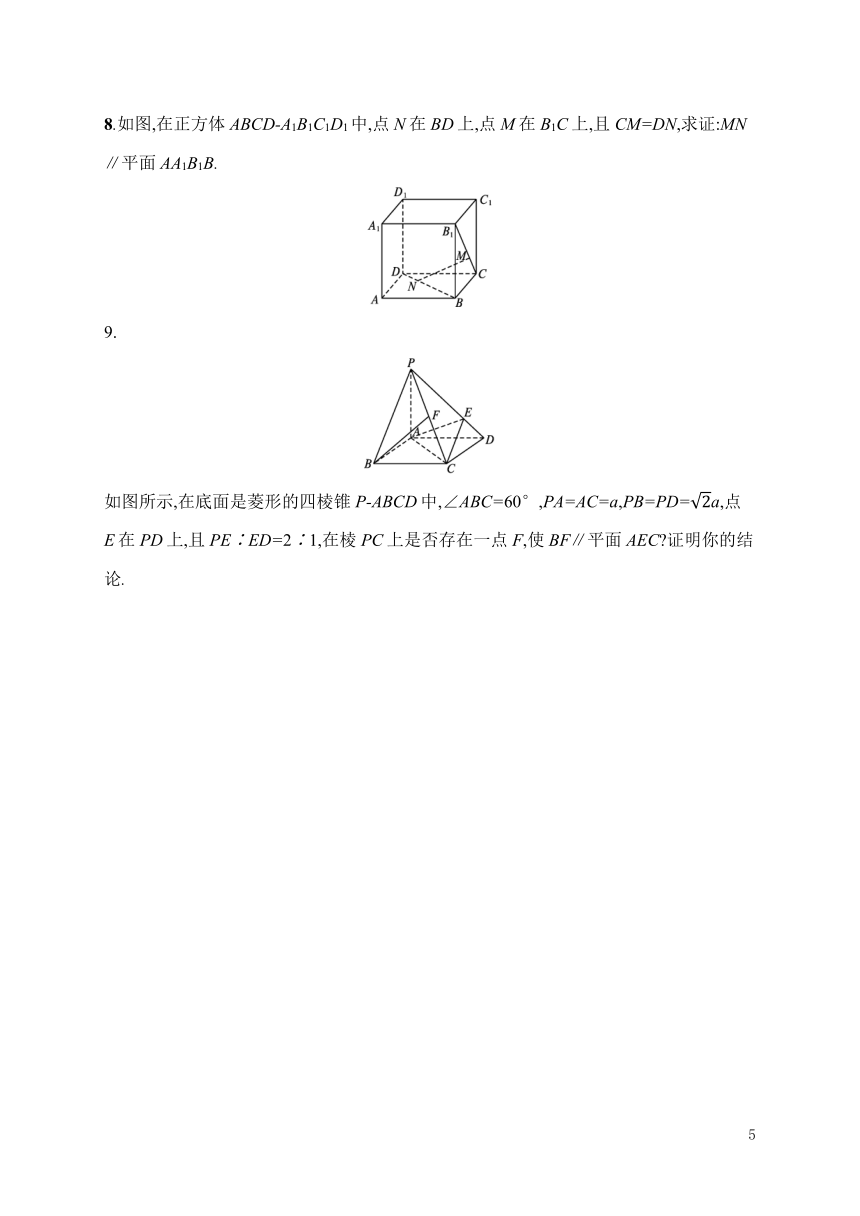
8.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
9.
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=a,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
答案
1.(多选题)设α,β为两个不重合的平面,则下列条件能得到α∥β的是( )
A.α内有无数条直线与β平行
B.平面α,β平行于同一平面
C.平面α,β平行于同一条直线
D.α内有两条相交直线与β平行
答案BD
解析对于A,若这无数条直线为无数条平行线,则无法得到α∥β,A错误;
对于B,平面α,β平行于同一平面,此时α∥β,B正确;
对于C,平面α,β平行于同一条直线,此时平面α,β可以相交,C错误;
对于D,由面面平行的判定定理可知,D正确.
2.(多选题)已知a,b表示两条不重合的直线,α,β,γ表示三个不重合的平面,给出下列命题,其中正确的是( )
A.若α∩γ=a,β∩γ=b,且a∥b,则α∥β
B.若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β
C.若a∥α,a∥β,则α∥β
D.若a?α,a∥β,α∩β=b,则a∥b
答案BD
解析对于A,若α∩γ=a,β∩γ=b,且a∥b,则α∥β或者α与β相交,故A错误.
对于B,若a,b相交且都在α,β外,则a,b可以确定一个平面,记为γ,a∥α,b∥α,a∥β,b∥β,可得γ∥α,γ∥β,由面面平行的传递性可知α∥β,故B正确.
对于C,a∥α,a∥β,则α∥β或α与β相交,故C错误.
对于D,由a?α,a∥β,α∩β=b,由线面平行的性质定理知a∥b,故D正确.
3.已知直线a,b,平面α,β,下列命题正确的是( )
A.若a∥α,b∥a,则b∥α
B.若a∥α,b∥α,a?β,b?β,则β∥α
C.若α∥β,b∥α,则b∥β
D.若α∥β,a?α,则a∥β
答案D
解析本题考查线面、面面平行的判定和性质.若a∥α,b∥a,则b∥α或b?α,故A错误;由面面平行的判定定理知B错误;若α∥β,b∥α,则b∥β或b?β,故C错误.故选D.
4.a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出六个命题:
①?a∥b;②?a∥b;③?α∥β;
④?α∥β;⑤?a∥α;⑥?a∥α.
其中正确的命题是( )
A.②③
B.①④⑤
C.①④
D.①③④
答案C
解析本题考查直线、平面的平行.由空间平行线的传递性,知①正确;②错误,a,b可能相交、平行或异面;③错误,α与β可能相交;由面面平行的传递性,知④正确;⑤⑥错误,a可能在α内.故选C.
5.在正方体EFGH-E1F1G1H1中,四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
答案A
解析如图易证E1G1∥平面EGH1,G1F∥平面EGH1.
又E1G1∩G1F=G1,E1G1,G1F?平面E1FG1.
所以平面E1FG1∥平面EGH1.即选项A符合,其他都相交.故选A.
6.在正方体ABCD-A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E,F,则四边形D1EBF的形状是
( )
A.矩形
B.菱形
C.平行四边形
D.正方形
答案C
解析因为平面和左右两个侧面分别交于ED1,BF,所以ED1∥BF,同理D1F∥EB,所以四边形D1EBF是平行四边形.故选C.
7.下列说法正确的是( )
A.平行于同一条直线的两个平面平行
B.平行于同一个平面的两个平面平行
C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行
D.若三条直线a,b,c两两平行,则在过直线a的平面中,有且只有一个平面与b,c均平行
答案B
解析平行于同一条直线的两个平面可以平行也可以相交,所以A错;B正确;C中没有指明这三个点在平面的同侧还是异侧,所以C不正确;因为过直线a的平面中,只要b,c不在其平面内,则与b,c均平行,所以D不正确.故选B.
8.过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是 .?
答案l∥A1C1
解析因为过A1,C1,B三点的平面与底面A1B1C1D1的交线为A1C1,与底面ABCD的交线为l,由于正方体的两底面互相平行,则由面面平行的性质定理知l∥A1C1.
9.
如图,ABCD是空间四边形,E,F,G,H分别是其四边上的点且共面,AC∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,= .?
答案
解析,而EF=FG,
∴EF=,
∴.
素养提升
1.已知a,b表示直线,α,β,γ表示平面,则下列推理正确的是( )
A.α∩β=a,b?α?a∥b
B.α∩β=a,a∥b?b∥α,且b∥β
C.a∥β,b∥β,a?α,b?α?α∥β
D.α∥β,α∩γ=a,β∩γ=b?a∥b
答案D
解析选项A,α∩β=a,b?α,则a,b可能平行也可能相交,故A不正确;
选项B,α∩β=a,a∥b,则可能b∥α,且b∥β,也可能b
在平面α或β内,故B不正确;
选项C,a∥β,b∥β,a?α,b?α,根据面面平行的判定定理,再加上条件a∩b=A,才能得出α∥β,故C不正确;
选项D为面面平行性质定理的符号语言,故选D.
2.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当A,B分别在α,β内运动时,那么所有的动点C( )
A.不共面
B.当且仅当A,B在两条相交直线上移动时才共面
C.当且仅当A,B在两条给定的平行直线上移动时才共面
D.不论A,B如何移动都共面
答案D
解析由面面平行的性质,不论A,B如何运动,动点C均在过点C且与α,β都平行的平面上.
3.
如图,在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上,平面AEF∥平面BD1G,则=( )
A.
B.
C.
D.
答案B
解析∵在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,∴EF∥BD1,
∵G在CC1上,且平面AEF∥平面BD1G,
∴AF∥BG,∴.
4.如图,P是△ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于点A',B',C',若,则=( )
A.
B.
C.
D.
答案D
解析由平面α∥平面ABC,得AB∥A'B',BC∥B'C',AC∥A'C',由等角定理得∠ABC=∠A'B'C',∠BCA=∠B'C'A',∠CAB=∠C'A'B',从而△ABC∽△A'B'C',△PAB∽△PA'B',,
所以,故选D.
5.
(多选题)如图是正四棱锥P-ABCD的平面展开图,其中四边形ABCD为正方形,P1,P2,P3,P4是顶点P对应的四个点,E,F,G,H分别为P1A,P4D,P2C,P2B的中点.在正四棱锥P-ABCD中,给出下列结论,其中正确的是
( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
答案ABC
解析作出立体图形如图所示.
连接E,F,G,H四点构成平面EFGH.对于A,因为E,F分别是PA,PD的中点,所以EF∥AD.又EF?平面ABCD,AD?平面ABCD,所以EF∥平面ABCD.同理,EH∥平面ABCD.又EF∩EH=E,EF?平面EFGH,EH?平面EFGH,所以平面EFGH∥平面ABCD,故A正确;
对于B,连接AC,BD,DG,BG,设AC的中点为M,则M也是BD的中点,所以MG∥PA,又MG?平面BDG,PA?平面BDG,所以PA∥平面BDG,故B正确;
对于C,由A中的分析知EF∥AD,AD∥BC,所以EF∥BC,因为EF?平面PBC,BC?平面PBC,所以直线EF∥平面PBC,故C正确;
对于D,根据C中的分析可知EF∥BC,再结合图形可得,BC∩BD=B,则直线EF与平面BDG不平行,故D错误.
6.如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.
则在四棱锥P-ABCD中,AP与平面EFG的位置关系为 .?
答案平行
解析在四棱锥P-ABCD中,∵E,F分别为PC,PD的中点,∴EF∥CD.∵AB∥CD,∴EF∥AB.
∵EF?平面PAB,AB?平面PAB,∴EF∥平面PAB.同理EG∥平面PAB.
又EF∩EG=E,∴平面EFG∥平面PAB.
∵AP?平面PAB,AP?平面EFG,∴AP∥平面EFG.
7.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线MD与平面A1ACC1的位置关系是 .直线MD与平面BCC1B1的位置关系是 .?
答案相交 平行
解析因为M是A1D1的中点,所以直线DM与直线AA1相交,所以DM与平面A1ACC1有一个公共点,所以DM与平面A1ACC1相交.
取B1C1中点M1,MM1?C1D1,C1D1?CD,
所以四边形DMM1C为平行四边形,所以DM?CM1,所以DM∥平面BCC1B1.
8.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
证明证法一:如图,作ME∥BC交B1B于点E,作NF∥AD交AB于点F,连接EF,
则EF?平面AA1B1B.
∴.
∵在正方体ABCD-A1B1C1D1中,CM=DN,
∴B1M=BN.
又B1M=BN,B1C=BD,
∴.
∴ME=NF.又ME∥BC∥AD∥NF,
∴四边形MEFN为平行四边形.
∴MN∥EF,∴MN∥平面AA1B1B.
证法二:如图,连接CN并延长交BA所在直线于点P,连接B1P.
则B1P?平面AA1B1B.
∵△NDC∽△NBP,∴.
又CM=DN,B1C=BD,
∴.
∴MN∥B1P.
∵B1P?平面AA1B1B,
∴MN∥平面AA1B1B.
9.
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=a,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
解当点F是棱PC的中点时,BF∥平面AEC.
证明:取PE的中点M,连接FM,则FM∥CE.
∵FM?平面AEC,CE?平面AEC,∴FM∥平面AEC,由EM=PE=ED,得E是MD的中点.
连接BM,BD,设BD∩AC=O,
则O是BD的中点,∴BM∥OE.
∵BM?平面AEC,OE?平面AEC,
∴BM∥平面AEC.
∵FM∩BM=M,∴平面BFM∥平面AEC.
又BF?平面BFM,∴BF∥平面AEC.
5
1.(多选题)设α,β为两个不重合的平面,则下列条件能得到α∥β的是( )
A.α内有无数条直线与β平行
B.平面α,β平行于同一平面
C.平面α,β平行于同一条直线
D.α内有两条相交直线与β平行
2.(多选题)已知a,b表示两条不重合的直线,α,β,γ表示三个不重合的平面,给出下列命题,其中正确的是( )
A.若α∩γ=a,β∩γ=b,且a∥b,则α∥β
B.若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β
C.若a∥α,a∥β,则α∥β
D.若a?α,a∥β,α∩β=b,则a∥b
3.已知直线a,b,平面α,β,下列命题正确的是( )
A.若a∥α,b∥a,则b∥α
B.若a∥α,b∥α,a?β,b?β,则β∥α
C.若α∥β,b∥α,则b∥β
D.若α∥β,a?α,则a∥β
4.a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出六个命题:
①?a∥b;②?a∥b;③?α∥β;
④?α∥β;⑤?a∥α;⑥?a∥α.
其中正确的命题是( )
A.②③
B.①④⑤
C.①④
D.①③④
5.在正方体EFGH-E1F1G1H1中,四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
6.在正方体ABCD-A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E,F,则四边形D1EBF的形状是
( )
A.矩形
B.菱形
C.平行四边形
D.正方形
7.下列说法正确的是( )
A.平行于同一条直线的两个平面平行
B.平行于同一个平面的两个平面平行
C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行
D.若三条直线a,b,c两两平行,则在过直线a的平面中,有且只有一个平面与b,c均平行
8.过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是 .?
9.
如图,ABCD是空间四边形,E,F,G,H分别是其四边上的点且共面,AC∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,= .?
素养提升
1.已知a,b表示直线,α,β,γ表示平面,则下列推理正确的是( )
A.α∩β=a,b?α?a∥b
B.α∩β=a,a∥b?b∥α,且b∥β
C.a∥β,b∥β,a?α,b?α?α∥β
D.α∥β,α∩γ=a,β∩γ=b?a∥b
2.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当A,B分别在α,β内运动时,那么所有的动点C( )
A.不共面
B.当且仅当A,B在两条相交直线上移动时才共面
C.当且仅当A,B在两条给定的平行直线上移动时才共面
D.不论A,B如何移动都共面
3.
如图,在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上,平面AEF∥平面BD1G,则=( )
A.
B.
C.
D.
4.如图,P是△ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于点A',B',C',若,则=( )
A.
B.
C.
D.
5.
(多选题)如图是正四棱锥P-ABCD的平面展开图,其中四边形ABCD为正方形,P1,P2,P3,P4是顶点P对应的四个点,E,F,G,H分别为P1A,P4D,P2C,P2B的中点.在正四棱锥P-ABCD中,给出下列结论,其中正确的是
( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
6.如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.
则在四棱锥P-ABCD中,AP与平面EFG的位置关系为 .?
7.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线MD与平面A1ACC1的位置关系是 .直线MD与平面BCC1B1的位置关系是 .?
8.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
9.
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=a,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
答案
1.(多选题)设α,β为两个不重合的平面,则下列条件能得到α∥β的是( )
A.α内有无数条直线与β平行
B.平面α,β平行于同一平面
C.平面α,β平行于同一条直线
D.α内有两条相交直线与β平行
答案BD
解析对于A,若这无数条直线为无数条平行线,则无法得到α∥β,A错误;
对于B,平面α,β平行于同一平面,此时α∥β,B正确;
对于C,平面α,β平行于同一条直线,此时平面α,β可以相交,C错误;
对于D,由面面平行的判定定理可知,D正确.
2.(多选题)已知a,b表示两条不重合的直线,α,β,γ表示三个不重合的平面,给出下列命题,其中正确的是( )
A.若α∩γ=a,β∩γ=b,且a∥b,则α∥β
B.若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β
C.若a∥α,a∥β,则α∥β
D.若a?α,a∥β,α∩β=b,则a∥b
答案BD
解析对于A,若α∩γ=a,β∩γ=b,且a∥b,则α∥β或者α与β相交,故A错误.
对于B,若a,b相交且都在α,β外,则a,b可以确定一个平面,记为γ,a∥α,b∥α,a∥β,b∥β,可得γ∥α,γ∥β,由面面平行的传递性可知α∥β,故B正确.
对于C,a∥α,a∥β,则α∥β或α与β相交,故C错误.
对于D,由a?α,a∥β,α∩β=b,由线面平行的性质定理知a∥b,故D正确.
3.已知直线a,b,平面α,β,下列命题正确的是( )
A.若a∥α,b∥a,则b∥α
B.若a∥α,b∥α,a?β,b?β,则β∥α
C.若α∥β,b∥α,则b∥β
D.若α∥β,a?α,则a∥β
答案D
解析本题考查线面、面面平行的判定和性质.若a∥α,b∥a,则b∥α或b?α,故A错误;由面面平行的判定定理知B错误;若α∥β,b∥α,则b∥β或b?β,故C错误.故选D.
4.a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,现给出六个命题:
①?a∥b;②?a∥b;③?α∥β;
④?α∥β;⑤?a∥α;⑥?a∥α.
其中正确的命题是( )
A.②③
B.①④⑤
C.①④
D.①③④
答案C
解析本题考查直线、平面的平行.由空间平行线的传递性,知①正确;②错误,a,b可能相交、平行或异面;③错误,α与β可能相交;由面面平行的传递性,知④正确;⑤⑥错误,a可能在α内.故选C.
5.在正方体EFGH-E1F1G1H1中,四对截面彼此平行的一对是( )
A.平面E1FG1与平面EGH1
B.平面FHG1与平面F1H1G
C.平面F1H1H与平面FHE1
D.平面E1HG1与平面EH1G
答案A
解析如图易证E1G1∥平面EGH1,G1F∥平面EGH1.
又E1G1∩G1F=G1,E1G1,G1F?平面E1FG1.
所以平面E1FG1∥平面EGH1.即选项A符合,其他都相交.故选A.
6.在正方体ABCD-A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E,F,则四边形D1EBF的形状是
( )
A.矩形
B.菱形
C.平行四边形
D.正方形
答案C
解析因为平面和左右两个侧面分别交于ED1,BF,所以ED1∥BF,同理D1F∥EB,所以四边形D1EBF是平行四边形.故选C.
7.下列说法正确的是( )
A.平行于同一条直线的两个平面平行
B.平行于同一个平面的两个平面平行
C.一个平面内有三个不共线的点到另一个平面的距离相等,则这两个平面平行
D.若三条直线a,b,c两两平行,则在过直线a的平面中,有且只有一个平面与b,c均平行
答案B
解析平行于同一条直线的两个平面可以平行也可以相交,所以A错;B正确;C中没有指明这三个点在平面的同侧还是异侧,所以C不正确;因为过直线a的平面中,只要b,c不在其平面内,则与b,c均平行,所以D不正确.故选B.
8.过正方体ABCD-A1B1C1D1的三个顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是 .?
答案l∥A1C1
解析因为过A1,C1,B三点的平面与底面A1B1C1D1的交线为A1C1,与底面ABCD的交线为l,由于正方体的两底面互相平行,则由面面平行的性质定理知l∥A1C1.
9.
如图,ABCD是空间四边形,E,F,G,H分别是其四边上的点且共面,AC∥平面EFGH,AC=m,BD=n,当EFGH是菱形时,= .?
答案
解析,而EF=FG,
∴EF=,
∴.
素养提升
1.已知a,b表示直线,α,β,γ表示平面,则下列推理正确的是( )
A.α∩β=a,b?α?a∥b
B.α∩β=a,a∥b?b∥α,且b∥β
C.a∥β,b∥β,a?α,b?α?α∥β
D.α∥β,α∩γ=a,β∩γ=b?a∥b
答案D
解析选项A,α∩β=a,b?α,则a,b可能平行也可能相交,故A不正确;
选项B,α∩β=a,a∥b,则可能b∥α,且b∥β,也可能b
在平面α或β内,故B不正确;
选项C,a∥β,b∥β,a?α,b?α,根据面面平行的判定定理,再加上条件a∩b=A,才能得出α∥β,故C不正确;
选项D为面面平行性质定理的符号语言,故选D.
2.设平面α∥平面β,A∈α,B∈β,C是AB的中点,当A,B分别在α,β内运动时,那么所有的动点C( )
A.不共面
B.当且仅当A,B在两条相交直线上移动时才共面
C.当且仅当A,B在两条给定的平行直线上移动时才共面
D.不论A,B如何移动都共面
答案D
解析由面面平行的性质,不论A,B如何运动,动点C均在过点C且与α,β都平行的平面上.
3.
如图,在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,G在CC1上,平面AEF∥平面BD1G,则=( )
A.
B.
C.
D.
答案B
解析∵在四棱柱ABCD-A1B1C1D1中,四边形ABCD为平行四边形,E,F分别在线段DB,DD1上,且,∴EF∥BD1,
∵G在CC1上,且平面AEF∥平面BD1G,
∴AF∥BG,∴.
4.如图,P是△ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于点A',B',C',若,则=( )
A.
B.
C.
D.
答案D
解析由平面α∥平面ABC,得AB∥A'B',BC∥B'C',AC∥A'C',由等角定理得∠ABC=∠A'B'C',∠BCA=∠B'C'A',∠CAB=∠C'A'B',从而△ABC∽△A'B'C',△PAB∽△PA'B',,
所以,故选D.
5.
(多选题)如图是正四棱锥P-ABCD的平面展开图,其中四边形ABCD为正方形,P1,P2,P3,P4是顶点P对应的四个点,E,F,G,H分别为P1A,P4D,P2C,P2B的中点.在正四棱锥P-ABCD中,给出下列结论,其中正确的是
( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
答案ABC
解析作出立体图形如图所示.
连接E,F,G,H四点构成平面EFGH.对于A,因为E,F分别是PA,PD的中点,所以EF∥AD.又EF?平面ABCD,AD?平面ABCD,所以EF∥平面ABCD.同理,EH∥平面ABCD.又EF∩EH=E,EF?平面EFGH,EH?平面EFGH,所以平面EFGH∥平面ABCD,故A正确;
对于B,连接AC,BD,DG,BG,设AC的中点为M,则M也是BD的中点,所以MG∥PA,又MG?平面BDG,PA?平面BDG,所以PA∥平面BDG,故B正确;
对于C,由A中的分析知EF∥AD,AD∥BC,所以EF∥BC,因为EF?平面PBC,BC?平面PBC,所以直线EF∥平面PBC,故C正确;
对于D,根据C中的分析可知EF∥BC,再结合图形可得,BC∩BD=B,则直线EF与平面BDG不平行,故D错误.
6.如图①,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP,D为AP的中点,E,F,G分别为PC,PD,CB的中点,将△PCD沿CD折起,得到四棱锥P-ABCD,如图②.
则在四棱锥P-ABCD中,AP与平面EFG的位置关系为 .?
答案平行
解析在四棱锥P-ABCD中,∵E,F分别为PC,PD的中点,∴EF∥CD.∵AB∥CD,∴EF∥AB.
∵EF?平面PAB,AB?平面PAB,∴EF∥平面PAB.同理EG∥平面PAB.
又EF∩EG=E,∴平面EFG∥平面PAB.
∵AP?平面PAB,AP?平面EFG,∴AP∥平面EFG.
7.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线MD与平面A1ACC1的位置关系是 .直线MD与平面BCC1B1的位置关系是 .?
答案相交 平行
解析因为M是A1D1的中点,所以直线DM与直线AA1相交,所以DM与平面A1ACC1有一个公共点,所以DM与平面A1ACC1相交.
取B1C1中点M1,MM1?C1D1,C1D1?CD,
所以四边形DMM1C为平行四边形,所以DM?CM1,所以DM∥平面BCC1B1.
8.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
证明证法一:如图,作ME∥BC交B1B于点E,作NF∥AD交AB于点F,连接EF,
则EF?平面AA1B1B.
∴.
∵在正方体ABCD-A1B1C1D1中,CM=DN,
∴B1M=BN.
又B1M=BN,B1C=BD,
∴.
∴ME=NF.又ME∥BC∥AD∥NF,
∴四边形MEFN为平行四边形.
∴MN∥EF,∴MN∥平面AA1B1B.
证法二:如图,连接CN并延长交BA所在直线于点P,连接B1P.
则B1P?平面AA1B1B.
∵△NDC∽△NBP,∴.
又CM=DN,B1C=BD,
∴.
∴MN∥B1P.
∵B1P?平面AA1B1B,
∴MN∥平面AA1B1B.
9.
如图所示,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=a,点E在PD上,且PE∶ED=2∶1,在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
解当点F是棱PC的中点时,BF∥平面AEC.
证明:取PE的中点M,连接FM,则FM∥CE.
∵FM?平面AEC,CE?平面AEC,∴FM∥平面AEC,由EM=PE=ED,得E是MD的中点.
连接BM,BD,设BD∩AC=O,
则O是BD的中点,∴BM∥OE.
∵BM?平面AEC,OE?平面AEC,
∴BM∥平面AEC.
∵FM∩BM=M,∴平面BFM∥平面AEC.
又BF?平面BFM,∴BF∥平面AEC.
5
