2020-2021学年高二数学人教B版(2019)必修第四册第十一章立体几何初步11.1.3 多面体与棱柱11.1.4 棱锥与棱台同步作业(Word版含解析)
文档属性
| 名称 | 2020-2021学年高二数学人教B版(2019)必修第四册第十一章立体几何初步11.1.3 多面体与棱柱11.1.4 棱锥与棱台同步作业(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 838.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 07:58:32 | ||
图片预览



文档简介
11.1.3 多面体与棱柱 11.1.4 棱锥与棱台
1.下列四种说法:
①底面是矩形的平行六面体是长方体;
②棱长相等的直四棱柱是正方体;
③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;
④侧面对角线相等的平行六面体是直平行六面体.
其中,正确的个数是( )
A.1
B.2
C.3
D.4
2.下列命题正确的是( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
C.若棱柱被一平面所截,则分成的两部分一定是棱柱
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
3.下列命题中正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.两个底面平行且相似,其余各面都是梯形的多面体是棱台
C.棱台的底面是两个相似的正方形
D.棱台的侧棱延长后必交于一点
4.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1
cm,高为5
cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.12
B.13
C.
D.15
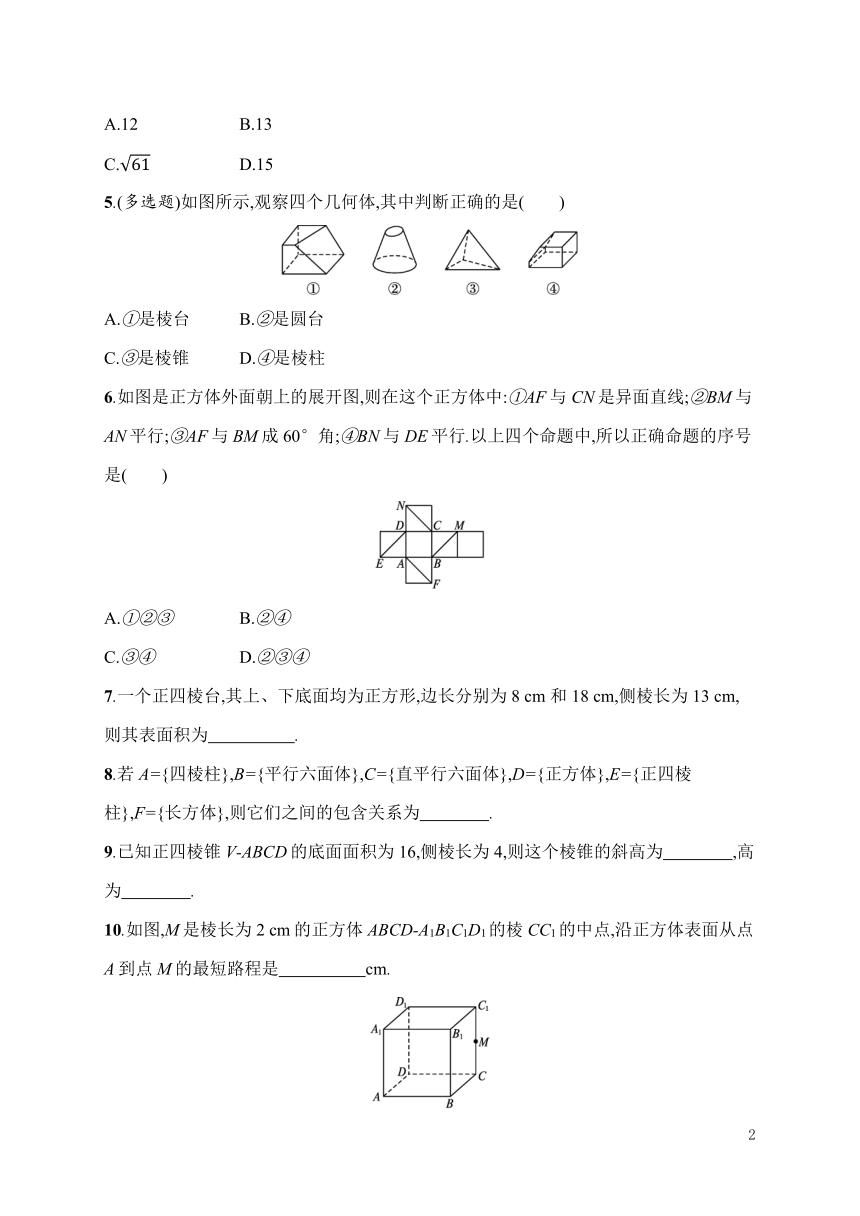
5.(多选题)如图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱柱
6.如图是正方体外面朝上的展开图,则在这个正方体中:①AF与CN是异面直线;②BM与AN平行;③AF与BM成60°角;④BN与DE平行.以上四个命题中,所以正确命题的序号是( )
A.①②③
B.②④
C.③④
D.②③④
7.一个正四棱台,其上、下底面均为正方形,边长分别为8
cm
和18
cm,侧棱长为13
cm,则其表面积为 .?
8.若A={四棱柱},B={平行六面体},C={直平行六面体},D={正方体},E={正四棱柱},F={长方体},则它们之间的包含关系为 .?
9.已知正四棱锥V-ABCD的底面面积为16,侧棱长为4,则这个棱锥的斜高为 ,高为 .?
10.如图,M是棱长为2
cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.?
11.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.
素养提升
1.
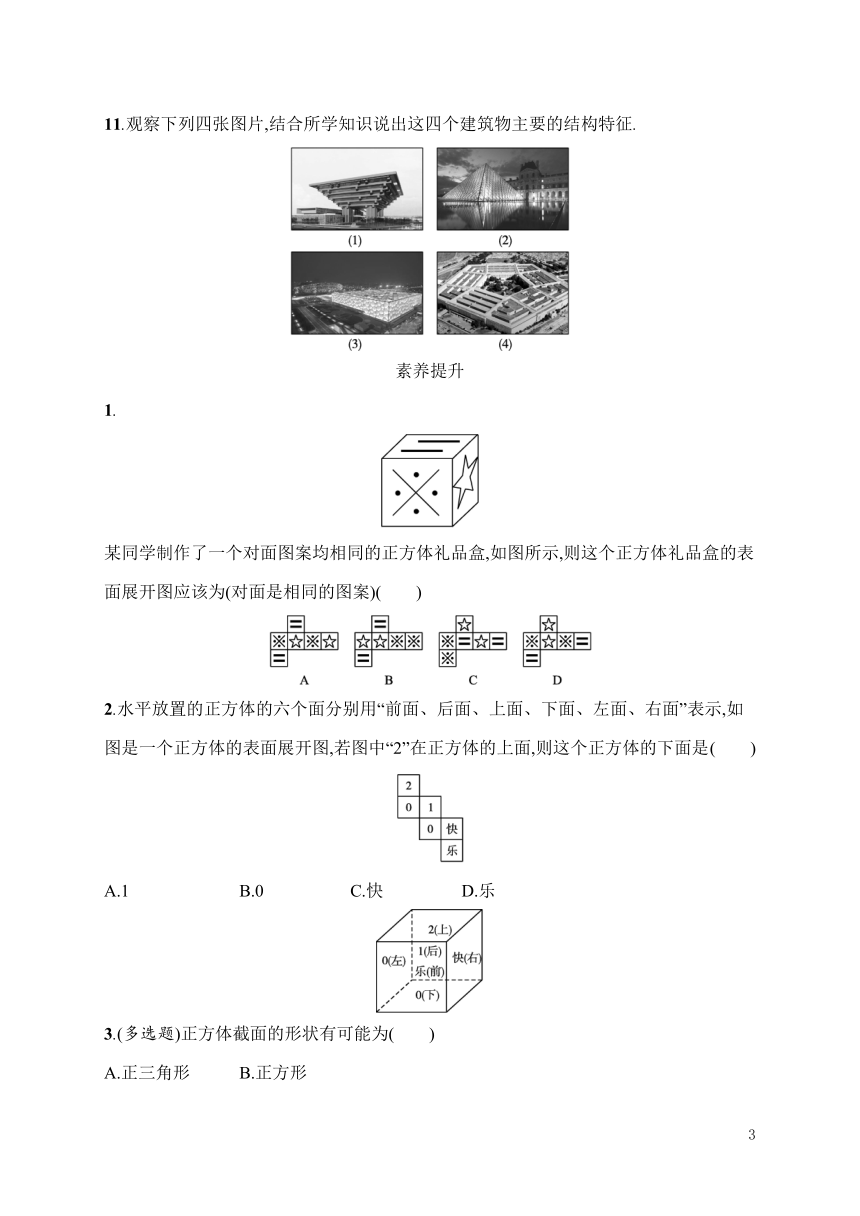
某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是
( )
A.1
B.0
C.快
D.乐
3.(多选题)正方体截面的形状有可能为( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
4.鲁班锁(也称孔明锁、难人木、六子联方)起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图①,这是一种常见的鲁班锁玩具,图②是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )
A.8(6+6)
B.6(8+8)
C.8(6+6)
D.6(8+8)
5.在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有 条.?
6.已知棱长为a,各面均为等边三角形的四面体S-ABC(即正四面体S-ABC),则其表面积为 .?
7.中国古代,建筑工匠们非常注重在建筑中体现数学美,方形和圆形的应用比比皆是.在唐、宋时期的单檐建筑中较多存在∶1的比例关系,这是当时工匠们着意设计的常见比例,今天,A4纸之所以流行的重要原因之一,就是它的长与宽的比无限接近∶1,我们称这种满足了∶1的矩形为“优美”矩形.现有一长方体ABCD-A1B1C1D1,AD1=2,AC=2,AC1=2,则此长方体的表面六个矩形中,“优美”矩形的个数为 .?
8.
正六棱锥被过棱锥高的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥的侧棱长为12
cm,小棱锥的底面边长为4
cm,求截得的棱台的侧面积与全面积.
9.在一个长方体的容器中,里面装有少量水,现在将容器绕着某底部的一条棱倾斜,在倾斜的过程中:
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,上面的第(1)题和第(2)题对不对?
答案
1.下列四种说法:
①底面是矩形的平行六面体是长方体;
②棱长相等的直四棱柱是正方体;
③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;
④侧面对角线相等的平行六面体是直平行六面体.
其中,正确的个数是( )
A.1
B.2
C.3
D.4
答案A
解析①不正确,除底面是矩形外还应满足侧棱与底面垂直才是长方体;②不正确,当底面是菱形时就不是正方体;③不正确,两条侧棱垂直于底面一边不一定垂直于底面,故不一定是直平行六面体;④正确,对角线相等的平行四边形是矩形,由此可以推测此时的平行六面体是直平行六面体.故选A.
2.下列命题正确的是( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
C.若棱柱被一平面所截,则分成的两部分一定是棱柱
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
答案B
解析对于A,如图①所示的几何体中有两个面平行,其余各面都是四边形,该几何体不是棱柱,故A不正确;对于B,由棱柱的定义可知正确;对于C,分成的两部分不一定是棱柱,故C不正确;对于D,如图②所示的几何体中有两个面平行,其余各面都是平行四边形,该几何体不是棱柱.
3.下列命题中正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.两个底面平行且相似,其余各面都是梯形的多面体是棱台
C.棱台的底面是两个相似的正方形
D.棱台的侧棱延长后必交于一点
答案D
解析A中的平面不一定平行于底面,故A错;B中侧棱不一定交于一点;C中底面不一定是正方形.故选D.
4.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1
cm,高为5
cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.12
B.13
C.
D.15
答案C
解析将正三棱柱ABC-A1B1C1沿侧棱展开,
再拼接一次,其侧面展开图如图所示,在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6×1=6,宽等于5,由勾股定理d=.
5.(多选题)如图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱柱
答案CD
解析题图①中的几何体不是由棱锥被一个平面所截得到的,且上、下底面不是相似的图形,所以不是棱台;
题图②中的几何体上、下两个面不平行,所以②不是圆台;题图③中的几何体是三棱锥;题图④中的几何体前、后两个面平行,其他面都是平行四边形,且每相邻两个平行四边形的公共边都互相平行,所以④是棱柱.
6.如图是正方体外面朝上的展开图,则在这个正方体中:①AF与CN是异面直线;②BM与AN平行;③AF与BM成60°角;④BN与DE平行.以上四个命题中,所以正确命题的序号是( )
A.①②③
B.②④
C.③④
D.②③④
答案A
解析将
正方体的展开图还原为正方体EFMN-ABCD,如图所示,可得AF与CN是异面直线,故①正确;连接AN,则BM与AN平行,故②正确;因为BM∥AN,
所以∠NAF是异面直线AF与BM所成的角,因为△NAF为等边三角形,所以∠NAF=60°,故③正确;BN与DE是异面直线,故④错误.
7.一个正四棱台,其上、下底面均为正方形,边长分别为8
cm
和18
cm,侧棱长为13
cm,则其表面积为 .?
答案1
012
cm2
解析由已知可得正四棱台侧面梯形的高为h==12(cm),
所以S侧=4××(8+18)×12=624(cm2),S上底=8×8=64(cm2),S下底=18×18=324(cm2),于是表面积为S=624+64+324=1
012(cm2).
8.若A={四棱柱},B={平行六面体},C={直平行六面体},D={正方体},E={正四棱柱},F={长方体},则它们之间的包含关系为 .?
答案D?E?F?C?B?A
解析四棱柱:底面是四边形的柱体是四棱柱;平行六面体:底面是平行四边形的四棱柱是平行六面体;直平行六面体:侧棱与底面垂直的平行六面体是直平行六面体;长方体:底面是长方形的直平行六面体是长方体;正四棱柱:底面是正方形的长方体是正四棱柱;正方体:各个面都是正方形的正四棱柱.根据以上概念,可得D?E?F?C?B?A.
9.已知正四棱锥V-ABCD的底面面积为16,侧棱长为4,则这个棱锥的斜高为 ,高为 .?
答案2 2
解析如图所示,
由题意知,正四棱锥底面边长为4,又侧棱长为4,所以侧面为等边三角形,取G为CD的中点,在等边三角形VCD中,VG=VC=2,V在平面ABCD的投影为正方形ABCD的中心O,在Rt△BCD中,DB==4.
则DO=DB=2,所以在Rt△VOD中,VO==2.
10.如图,M是棱长为2
cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.?
答案
解析由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2
cm,3
cm,故两点之间的距离是
cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是
cm.故沿正方体表面从点A到点M的最短路程是
cm.
11.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.
解(1)是上海世博会中国馆,其主体结构是四棱台.
(2)是法国卢浮宫,其主体结构是四棱锥.
(3)是国家游泳中心“水立方”,其主体结构是四棱柱.
(4)是美国五角大楼,其主体结构是五棱柱.
素养提升
1.
某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
答案A
解析根据正方体礼品盒的表面展开图的对面是相同的图案可知,展开图同图案不能相邻,B,C,D中都有相同的图案相邻,故选A.
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是
( )
A.1
B.0
C.快
D.乐
答案B
解析如图得到正方体,从图中可以看到“1”在正方体的后面,“快”在正方体的右面,“乐”在前面,下面、左面均为“0”.故选B.
3.(多选题)正方体截面的形状有可能为( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
答案ABD
解析画出截面图形如图,
可以画出正三角形但不是直角三角形(如图①);可以画出正方形(如图②);经过正方体的一个顶点去切就可得到五边形.但此时不可能是正五边形(如图③);正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,且可以画出正六边形(如图④).故选ABD.
4.鲁班锁(也称孔明锁、难人木、六子联方)起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图①,这是一种常见的鲁班锁玩具,图②是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )
A.8(6+6)
B.6(8+8)
C.8(6+6)
D.6(8+8)
答案A
解析由题图可知,该鲁班锁玩具可以看成是一个棱长为2+2的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为2,侧棱长为,则该几何体的表面积为S=6×[(2+2)2-4×]+8××2×=8(6+6).故选A.
5.在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有 条.?
答案10
解析在上底面选一个顶点,同时在下底选一个顶点,且这两个顶点不在同一侧面上,这样上底面每个顶点对应两条对角线,所以共有10条.
6.已知棱长为a,各面均为等边三角形的四面体S-ABC(即正四面体S-ABC),则其表面积为 .?
答案a2
解析由于四面体S-ABC的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.所以S△SBC=a2sin
60°=a2.
因此,四面体S-ABC的表面积S=4×a2=a2.
7.中国古代,建筑工匠们非常注重在建筑中体现数学美,方形和圆形的应用比比皆是.在唐、宋时期的单檐建筑中较多存在∶1的比例关系,这是当时工匠们着意设计的常见比例,今天,A4纸之所以流行的重要原因之一,就是它的长与宽的比无限接近∶1,我们称这种满足了∶1的矩形为“优美”矩形.现有一长方体ABCD-A1B1C1D1,AD1=2,AC=2,AC1=2,则此长方体的表面六个矩形中,“优美”矩形的个数为 .?
答案4
解析由题意,
该长方体如图所示,∵AD1=2,AC=2,AC1=2,
∴CC1==2,AD==4,
CD==2,
∴AB=CD=2,AA1=CC1=2,∴.
=2,∴此长方体的表面六个矩形中,“优美”矩形的个数为4.
8.
正六棱锥被过棱锥高的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥的侧棱长为12
cm,小棱锥的底面边长为4
cm,求截得的棱台的侧面积与全面积.
解(1)设小棱锥的底面边长为a,斜高为h,则大棱锥的底面边长为2a,斜高为2h,∴S大棱锥侧=6××2a×2h=12ah,S小棱锥侧=6×ah=3ah,
∴棱台的侧面积为12ah-3ah=9ah,因此,大棱锥、小棱锥、棱台的侧面积之比为4∶1∶3.
(2)∵小棱锥底面边长为4
cm,∴大棱锥底面边长为8
cm.∵大棱锥的侧棱长为12
cm,
∴其斜高为=8(cm),
∴S大棱锥侧=6××8×8=192(cm2),
∴棱台的侧面积为×192=144(cm2),S棱台上底面=6××42=24(cm2),S棱台下底面=6××82=96(cm2),
∴S棱台全=144+120(cm2).故棱台的侧面积为144
cm2,全面积为(144+120)cm2.
9.在一个长方体的容器中,里面装有少量水,现在将容器绕着某底部的一条棱倾斜,在倾斜的过程中:
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,上面的第(1)题和第(2)题对不对?
解(1)不对.水面的形状就是用一个与棱(倾斜时固定不动的棱)平行的平面截长方体时截面的形状,因而可以是矩形,但不可能是其他非矩形的平行四边形.
(2)不对.水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余部分的几何体,此几何体是棱柱,水比较少量,是三棱柱,水多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3)①不对.只有一条棱着地水面才是矩形;②不对.只有一条棱着地水才是棱柱.
4
1.下列四种说法:
①底面是矩形的平行六面体是长方体;
②棱长相等的直四棱柱是正方体;
③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;
④侧面对角线相等的平行六面体是直平行六面体.
其中,正确的个数是( )
A.1
B.2
C.3
D.4
2.下列命题正确的是( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
C.若棱柱被一平面所截,则分成的两部分一定是棱柱
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
3.下列命题中正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.两个底面平行且相似,其余各面都是梯形的多面体是棱台
C.棱台的底面是两个相似的正方形
D.棱台的侧棱延长后必交于一点
4.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1
cm,高为5
cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.12
B.13
C.
D.15
5.(多选题)如图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱柱
6.如图是正方体外面朝上的展开图,则在这个正方体中:①AF与CN是异面直线;②BM与AN平行;③AF与BM成60°角;④BN与DE平行.以上四个命题中,所以正确命题的序号是( )
A.①②③
B.②④
C.③④
D.②③④
7.一个正四棱台,其上、下底面均为正方形,边长分别为8
cm
和18
cm,侧棱长为13
cm,则其表面积为 .?
8.若A={四棱柱},B={平行六面体},C={直平行六面体},D={正方体},E={正四棱柱},F={长方体},则它们之间的包含关系为 .?
9.已知正四棱锥V-ABCD的底面面积为16,侧棱长为4,则这个棱锥的斜高为 ,高为 .?
10.如图,M是棱长为2
cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.?
11.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.
素养提升
1.
某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是
( )
A.1
B.0
C.快
D.乐
3.(多选题)正方体截面的形状有可能为( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
4.鲁班锁(也称孔明锁、难人木、六子联方)起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图①,这是一种常见的鲁班锁玩具,图②是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )
A.8(6+6)
B.6(8+8)
C.8(6+6)
D.6(8+8)
5.在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有 条.?
6.已知棱长为a,各面均为等边三角形的四面体S-ABC(即正四面体S-ABC),则其表面积为 .?
7.中国古代,建筑工匠们非常注重在建筑中体现数学美,方形和圆形的应用比比皆是.在唐、宋时期的单檐建筑中较多存在∶1的比例关系,这是当时工匠们着意设计的常见比例,今天,A4纸之所以流行的重要原因之一,就是它的长与宽的比无限接近∶1,我们称这种满足了∶1的矩形为“优美”矩形.现有一长方体ABCD-A1B1C1D1,AD1=2,AC=2,AC1=2,则此长方体的表面六个矩形中,“优美”矩形的个数为 .?
8.
正六棱锥被过棱锥高的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥的侧棱长为12
cm,小棱锥的底面边长为4
cm,求截得的棱台的侧面积与全面积.
9.在一个长方体的容器中,里面装有少量水,现在将容器绕着某底部的一条棱倾斜,在倾斜的过程中:
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,上面的第(1)题和第(2)题对不对?
答案
1.下列四种说法:
①底面是矩形的平行六面体是长方体;
②棱长相等的直四棱柱是正方体;
③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;
④侧面对角线相等的平行六面体是直平行六面体.
其中,正确的个数是( )
A.1
B.2
C.3
D.4
答案A
解析①不正确,除底面是矩形外还应满足侧棱与底面垂直才是长方体;②不正确,当底面是菱形时就不是正方体;③不正确,两条侧棱垂直于底面一边不一定垂直于底面,故不一定是直平行六面体;④正确,对角线相等的平行四边形是矩形,由此可以推测此时的平行六面体是直平行六面体.故选A.
2.下列命题正确的是( )
A.有两个面平行,其余各面都是四边形的几何体是棱柱
B.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱
C.若棱柱被一平面所截,则分成的两部分一定是棱柱
D.有两个面平行,其余各面都是平行四边形的几何体是棱柱
答案B
解析对于A,如图①所示的几何体中有两个面平行,其余各面都是四边形,该几何体不是棱柱,故A不正确;对于B,由棱柱的定义可知正确;对于C,分成的两部分不一定是棱柱,故C不正确;对于D,如图②所示的几何体中有两个面平行,其余各面都是平行四边形,该几何体不是棱柱.
3.下列命题中正确的是( )
A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台
B.两个底面平行且相似,其余各面都是梯形的多面体是棱台
C.棱台的底面是两个相似的正方形
D.棱台的侧棱延长后必交于一点
答案D
解析A中的平面不一定平行于底面,故A错;B中侧棱不一定交于一点;C中底面不一定是正方形.故选D.
4.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1
cm,高为5
cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )
A.12
B.13
C.
D.15
答案C
解析将正三棱柱ABC-A1B1C1沿侧棱展开,
再拼接一次,其侧面展开图如图所示,在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6×1=6,宽等于5,由勾股定理d=.
5.(多选题)如图所示,观察四个几何体,其中判断正确的是( )
A.①是棱台
B.②是圆台
C.③是棱锥
D.④是棱柱
答案CD
解析题图①中的几何体不是由棱锥被一个平面所截得到的,且上、下底面不是相似的图形,所以不是棱台;
题图②中的几何体上、下两个面不平行,所以②不是圆台;题图③中的几何体是三棱锥;题图④中的几何体前、后两个面平行,其他面都是平行四边形,且每相邻两个平行四边形的公共边都互相平行,所以④是棱柱.
6.如图是正方体外面朝上的展开图,则在这个正方体中:①AF与CN是异面直线;②BM与AN平行;③AF与BM成60°角;④BN与DE平行.以上四个命题中,所以正确命题的序号是( )
A.①②③
B.②④
C.③④
D.②③④
答案A
解析将
正方体的展开图还原为正方体EFMN-ABCD,如图所示,可得AF与CN是异面直线,故①正确;连接AN,则BM与AN平行,故②正确;因为BM∥AN,
所以∠NAF是异面直线AF与BM所成的角,因为△NAF为等边三角形,所以∠NAF=60°,故③正确;BN与DE是异面直线,故④错误.
7.一个正四棱台,其上、下底面均为正方形,边长分别为8
cm
和18
cm,侧棱长为13
cm,则其表面积为 .?
答案1
012
cm2
解析由已知可得正四棱台侧面梯形的高为h==12(cm),
所以S侧=4××(8+18)×12=624(cm2),S上底=8×8=64(cm2),S下底=18×18=324(cm2),于是表面积为S=624+64+324=1
012(cm2).
8.若A={四棱柱},B={平行六面体},C={直平行六面体},D={正方体},E={正四棱柱},F={长方体},则它们之间的包含关系为 .?
答案D?E?F?C?B?A
解析四棱柱:底面是四边形的柱体是四棱柱;平行六面体:底面是平行四边形的四棱柱是平行六面体;直平行六面体:侧棱与底面垂直的平行六面体是直平行六面体;长方体:底面是长方形的直平行六面体是长方体;正四棱柱:底面是正方形的长方体是正四棱柱;正方体:各个面都是正方形的正四棱柱.根据以上概念,可得D?E?F?C?B?A.
9.已知正四棱锥V-ABCD的底面面积为16,侧棱长为4,则这个棱锥的斜高为 ,高为 .?
答案2 2
解析如图所示,
由题意知,正四棱锥底面边长为4,又侧棱长为4,所以侧面为等边三角形,取G为CD的中点,在等边三角形VCD中,VG=VC=2,V在平面ABCD的投影为正方形ABCD的中心O,在Rt△BCD中,DB==4.
则DO=DB=2,所以在Rt△VOD中,VO==2.
10.如图,M是棱长为2
cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.?
答案
解析由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2
cm,3
cm,故两点之间的距离是
cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是
cm.故沿正方体表面从点A到点M的最短路程是
cm.
11.观察下列四张图片,结合所学知识说出这四个建筑物主要的结构特征.
解(1)是上海世博会中国馆,其主体结构是四棱台.
(2)是法国卢浮宫,其主体结构是四棱锥.
(3)是国家游泳中心“水立方”,其主体结构是四棱柱.
(4)是美国五角大楼,其主体结构是五棱柱.
素养提升
1.
某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
答案A
解析根据正方体礼品盒的表面展开图的对面是相同的图案可知,展开图同图案不能相邻,B,C,D中都有相同的图案相邻,故选A.
2.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是
( )
A.1
B.0
C.快
D.乐
答案B
解析如图得到正方体,从图中可以看到“1”在正方体的后面,“快”在正方体的右面,“乐”在前面,下面、左面均为“0”.故选B.
3.(多选题)正方体截面的形状有可能为( )
A.正三角形
B.正方形
C.正五边形
D.正六边形
答案ABD
解析画出截面图形如图,
可以画出正三角形但不是直角三角形(如图①);可以画出正方形(如图②);经过正方体的一个顶点去切就可得到五边形.但此时不可能是正五边形(如图③);正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,且可以画出正六边形(如图④).故选ABD.
4.鲁班锁(也称孔明锁、难人木、六子联方)起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图①,这是一种常见的鲁班锁玩具,图②是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )
A.8(6+6)
B.6(8+8)
C.8(6+6)
D.6(8+8)
答案A
解析由题图可知,该鲁班锁玩具可以看成是一个棱长为2+2的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为2,侧棱长为,则该几何体的表面积为S=6×[(2+2)2-4×]+8××2×=8(6+6).故选A.
5.在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有 条.?
答案10
解析在上底面选一个顶点,同时在下底选一个顶点,且这两个顶点不在同一侧面上,这样上底面每个顶点对应两条对角线,所以共有10条.
6.已知棱长为a,各面均为等边三角形的四面体S-ABC(即正四面体S-ABC),则其表面积为 .?
答案a2
解析由于四面体S-ABC的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.所以S△SBC=a2sin
60°=a2.
因此,四面体S-ABC的表面积S=4×a2=a2.
7.中国古代,建筑工匠们非常注重在建筑中体现数学美,方形和圆形的应用比比皆是.在唐、宋时期的单檐建筑中较多存在∶1的比例关系,这是当时工匠们着意设计的常见比例,今天,A4纸之所以流行的重要原因之一,就是它的长与宽的比无限接近∶1,我们称这种满足了∶1的矩形为“优美”矩形.现有一长方体ABCD-A1B1C1D1,AD1=2,AC=2,AC1=2,则此长方体的表面六个矩形中,“优美”矩形的个数为 .?
答案4
解析由题意,
该长方体如图所示,∵AD1=2,AC=2,AC1=2,
∴CC1==2,AD==4,
CD==2,
∴AB=CD=2,AA1=CC1=2,∴.
=2,∴此长方体的表面六个矩形中,“优美”矩形的个数为4.
8.
正六棱锥被过棱锥高的中点且平行于底面的平面所截,得到正六棱台和较小的棱锥.
(1)求大棱锥、小棱锥、棱台的侧面积之比;
(2)若大棱锥的侧棱长为12
cm,小棱锥的底面边长为4
cm,求截得的棱台的侧面积与全面积.
解(1)设小棱锥的底面边长为a,斜高为h,则大棱锥的底面边长为2a,斜高为2h,∴S大棱锥侧=6××2a×2h=12ah,S小棱锥侧=6×ah=3ah,
∴棱台的侧面积为12ah-3ah=9ah,因此,大棱锥、小棱锥、棱台的侧面积之比为4∶1∶3.
(2)∵小棱锥底面边长为4
cm,∴大棱锥底面边长为8
cm.∵大棱锥的侧棱长为12
cm,
∴其斜高为=8(cm),
∴S大棱锥侧=6××8×8=192(cm2),
∴棱台的侧面积为×192=144(cm2),S棱台上底面=6××42=24(cm2),S棱台下底面=6××82=96(cm2),
∴S棱台全=144+120(cm2).故棱台的侧面积为144
cm2,全面积为(144+120)cm2.
9.在一个长方体的容器中,里面装有少量水,现在将容器绕着某底部的一条棱倾斜,在倾斜的过程中:
(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)水的形状不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,上面的第(1)题和第(2)题对不对?
解(1)不对.水面的形状就是用一个与棱(倾斜时固定不动的棱)平行的平面截长方体时截面的形状,因而可以是矩形,但不可能是其他非矩形的平行四边形.
(2)不对.水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余部分的几何体,此几何体是棱柱,水比较少量,是三棱柱,水多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.
(3)①不对.只有一条棱着地水面才是矩形;②不对.只有一条棱着地水才是棱柱.
4
