2020-2021学年八年级数学人教版下册18.1.1平行四边形的性质 同步习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.1.1平行四边形的性质 同步习题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 157.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 09:08:10 | ||
图片预览


文档简介
18.1.1平行四边形的性质
同步习题
一、单选题
1.下列关于平行四边形的特征的描述中,正确的个数有(
)
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个
B.5个
C.3个
D.4个
2.如图,已知在中,,则(
)
A.18°
B.36°
C.45°
D.72°
3.下面关于平行四边形的说法不正确的是(
)
A.对边平行且相等
B.两组对角分别相等
C.对角线互相平分
D.每条对角线平分一组对角
4.在?ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
5.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
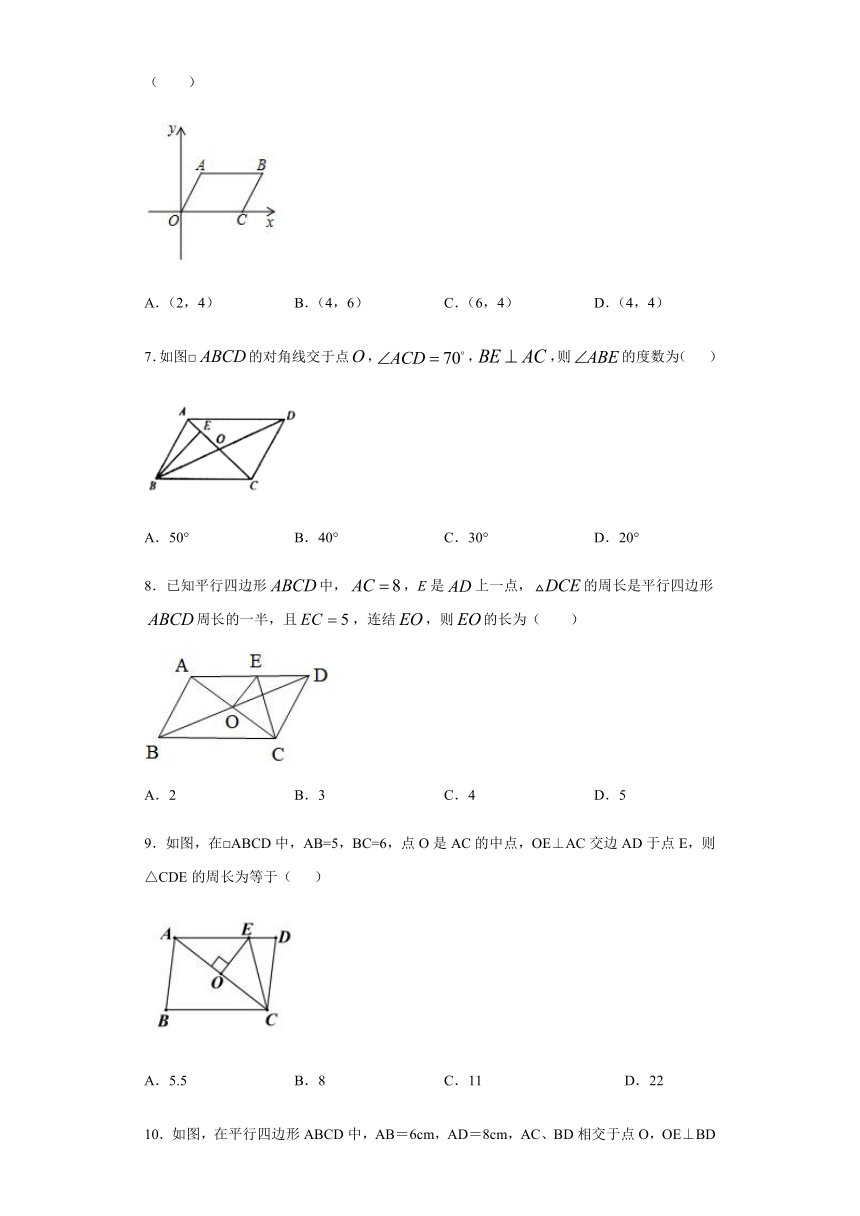
6.如图,四边形OABC是平行四边形,已知点A(2,4),点C(4,0),则点B的坐标为( )
A.(2,4)
B.(4,6)
C.(6,4)
D.(4,4)
7.如图□的对角线交于点,,,则的度数为(
)
A.50°
B.40°
C.30°
D.20°
8.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
9.如图,在□ABCD中,AB=5,BC=6,点O是AC的中点,OE⊥AC交边AD于点E,则△CDE的周长为等于(
)
A.5.5
B.8
C.11
D.22
10.如图,在平行四边形ABCD中,AB=6cm,AD=8cm,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( ).
A.12cm
B.14cm
C.16cm
D.28cm
二、填空题
11.在平行四边形中,若,则__________.
12.如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=
________
cm.
13.□ABCD的周长为16,其对角线AC与BD相交于点O,△AOB的周长比△BOC的周长大2,则边AB的长为_______.
14.如图,的对角线、相交于点O,过点O的直线交、的延长线于点E、F.若,,则__________.
15.如图,是的对角线交点,为中点,交于点,若.则的值为__________.
三、解答题
16.如图,在?ABCD中,CE平分∠BCD交AD于E,BF平分∠ABC交AD于F,若AB=6,BC=4,求EF的长.
17.证明题:如图,在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠BEF=∠DFE.
18.如图,在中,点是对角线的交点,过点且垂直于.
(1)求证:;
(2)若,,求的长.
参考答案
1.C
2.B
3.D
4.D
5.D
6.C
7.D
8.B
9.C
10.B
11.50°
12.4
13.5
14.5
15.
16.8
17.证明:∵四边形ABCD是平行四边形(已知),
∴AB=CD,AB∥CD
(平行四边形的对边平行且相等),
∴∠BAE=∠DCF(两直线平行,内错角相等),
在△ABE和△CDF中,
∵,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠DFC,
∴∠BEF=∠DFE.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S□ABCD=
AD×EF=63
∴AD=9.
同步习题
一、单选题
1.下列关于平行四边形的特征的描述中,正确的个数有(
)
(1)对边相等;(2)对角相等;(3)对角线相等;(4)邻边相等;(5)邻角互补.
A.2个
B.5个
C.3个
D.4个
2.如图,已知在中,,则(
)
A.18°
B.36°
C.45°
D.72°
3.下面关于平行四边形的说法不正确的是(
)
A.对边平行且相等
B.两组对角分别相等
C.对角线互相平分
D.每条对角线平分一组对角
4.在?ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A.3
B.5
C.2或3
D.3或5
5.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
6.如图,四边形OABC是平行四边形,已知点A(2,4),点C(4,0),则点B的坐标为( )
A.(2,4)
B.(4,6)
C.(6,4)
D.(4,4)
7.如图□的对角线交于点,,,则的度数为(
)
A.50°
B.40°
C.30°
D.20°
8.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
9.如图,在□ABCD中,AB=5,BC=6,点O是AC的中点,OE⊥AC交边AD于点E,则△CDE的周长为等于(
)
A.5.5
B.8
C.11
D.22
10.如图,在平行四边形ABCD中,AB=6cm,AD=8cm,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( ).
A.12cm
B.14cm
C.16cm
D.28cm
二、填空题
11.在平行四边形中,若,则__________.
12.如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=
________
cm.
13.□ABCD的周长为16,其对角线AC与BD相交于点O,△AOB的周长比△BOC的周长大2,则边AB的长为_______.
14.如图,的对角线、相交于点O,过点O的直线交、的延长线于点E、F.若,,则__________.
15.如图,是的对角线交点,为中点,交于点,若.则的值为__________.
三、解答题
16.如图,在?ABCD中,CE平分∠BCD交AD于E,BF平分∠ABC交AD于F,若AB=6,BC=4,求EF的长.
17.证明题:如图,在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
求证:∠BEF=∠DFE.
18.如图,在中,点是对角线的交点,过点且垂直于.
(1)求证:;
(2)若,,求的长.
参考答案
1.C
2.B
3.D
4.D
5.D
6.C
7.D
8.B
9.C
10.B
11.50°
12.4
13.5
14.5
15.
16.8
17.证明:∵四边形ABCD是平行四边形(已知),
∴AB=CD,AB∥CD
(平行四边形的对边平行且相等),
∴∠BAE=∠DCF(两直线平行,内错角相等),
在△ABE和△CDF中,
∵,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠DFC,
∴∠BEF=∠DFE.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴ADBC,OA=OC,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AEO≌△CFO(ASA)
∴OE=OF;
(2)∵OE=OF,OE=3.5,
∴EF=2OE=7,
又∵EF⊥AD,
∴S□ABCD=
AD×EF=63
∴AD=9.
