高中物理必修Ⅰ人教版3.5力的分解(35张ppt)
文档属性
| 名称 | 高中物理必修Ⅰ人教版3.5力的分解(35张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-07 08:48:21 | ||
图片预览

文档简介
(共35张PPT)
力的分解
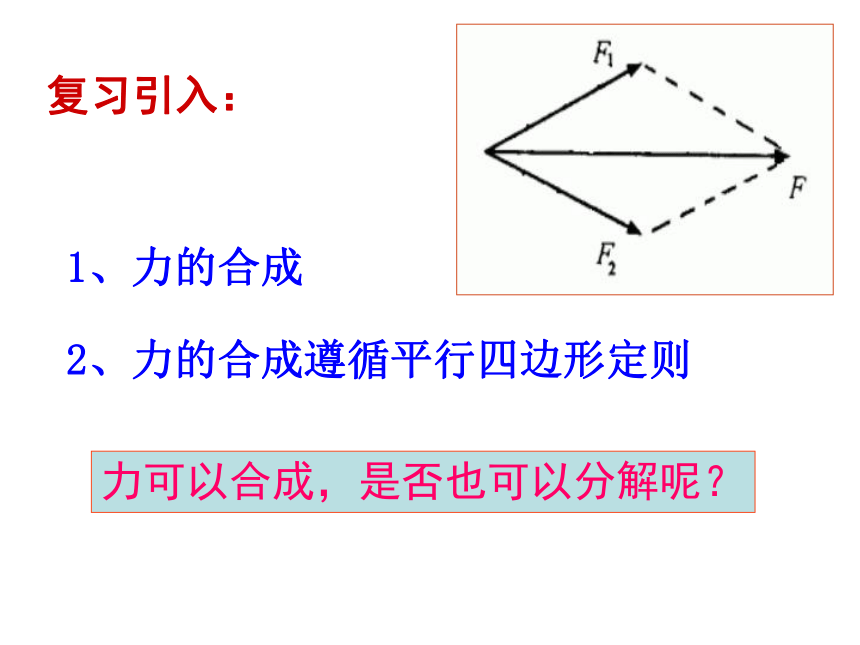
1、力的合成
2、力的合成遵循平行四边形定则
复习引入:
力可以合成,是否也可以分解呢?
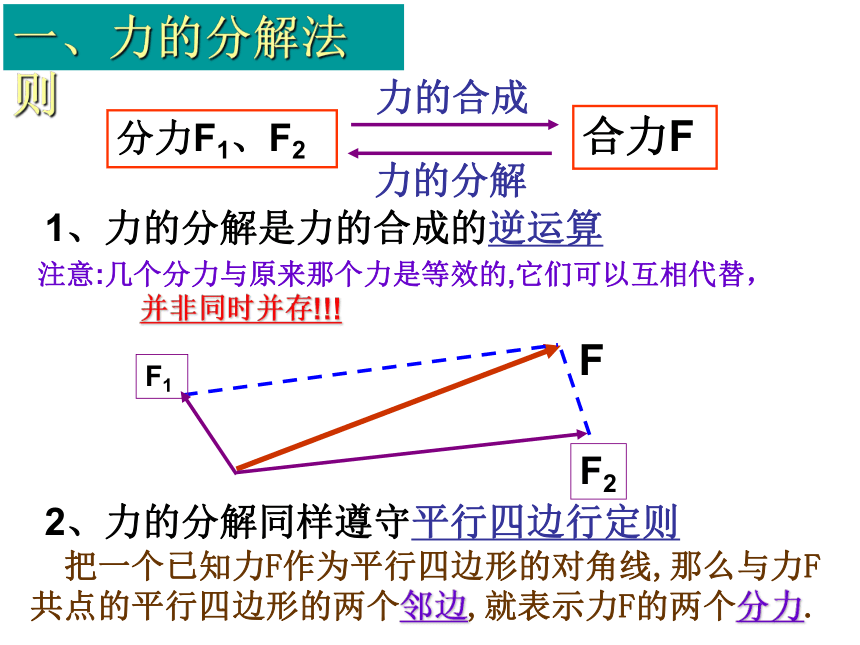
一、力的分解法则
1、力的分解是力的合成的逆运算
2、力的分解同样遵守平行四边行定则
F
F1
F2
分力F1、F2
合力F
力的合成
力的分解
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
注意:几个分力与原来那个力是等效的,它们可以互相代替,
并非同时并存!!!
F
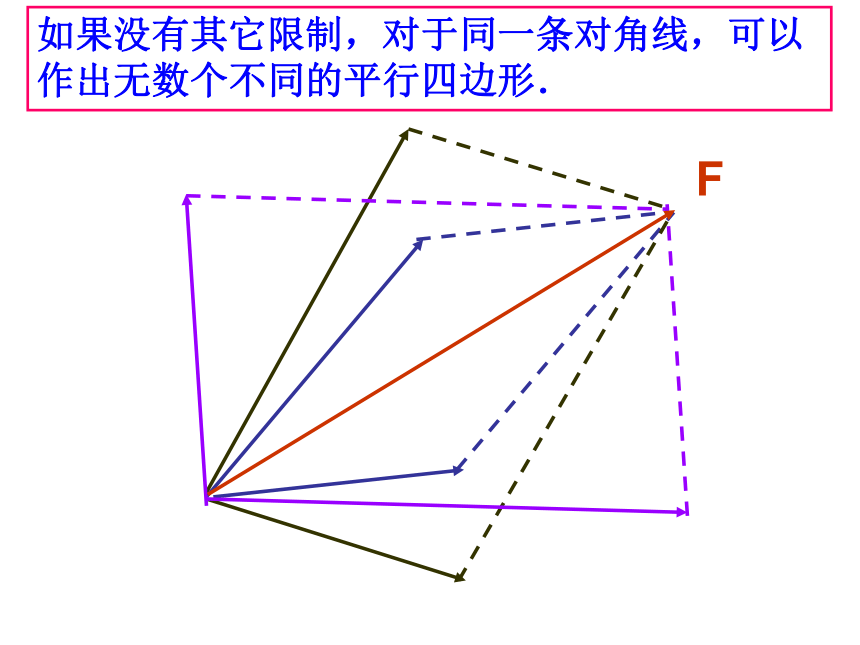
如果没有其它限制,对于同一条对角线,可以作出无数个不同的平行四边形.
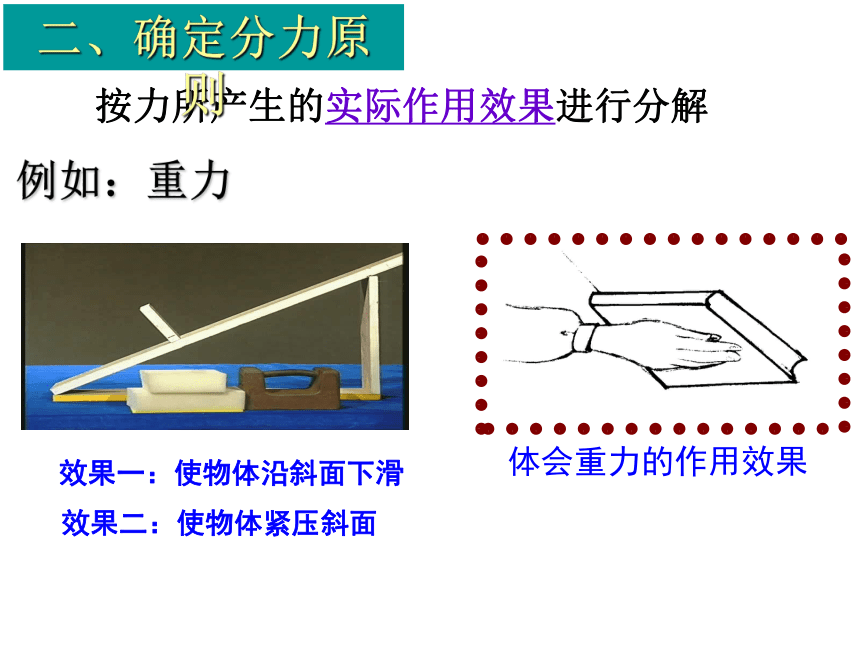
按力所产生的实际作用效果进行分解
二、确定分力原则
例如:重力
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
体会重力的作用效果
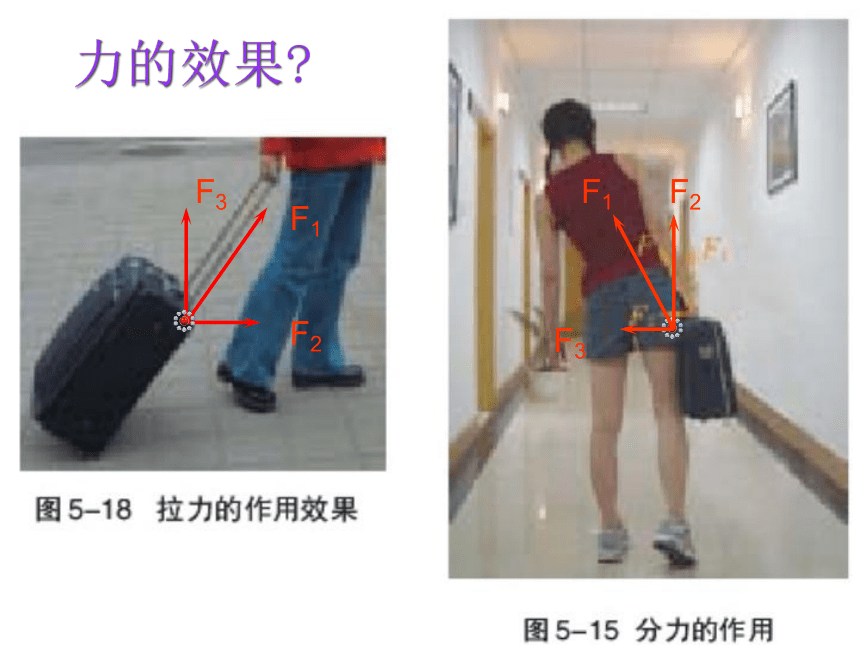
F1
F2
F3
F1
F2
F3
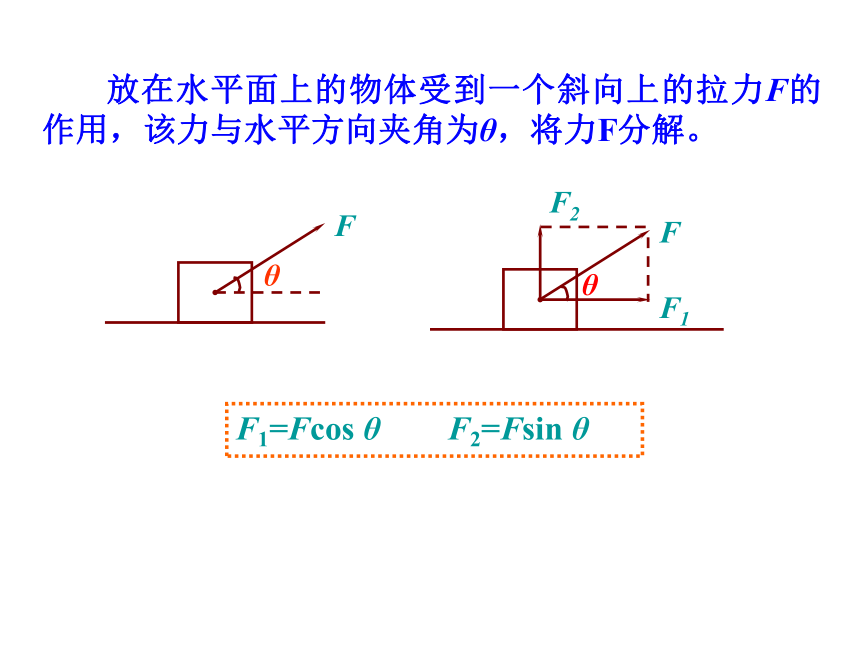
放在水平面上的物体受到一个斜向上的拉力F的作用,该力与水平方向夹角为θ,将力F分解。
F1=Fcos
θ F2=Fsin
θ
θ
F
F
θ
F1
F2
F
F
F1
F2
G
G2
G1
θ
G
G2
G1
G
G2
G1
F
Fa
Fb
a
b
F
F1
F2
G
θ
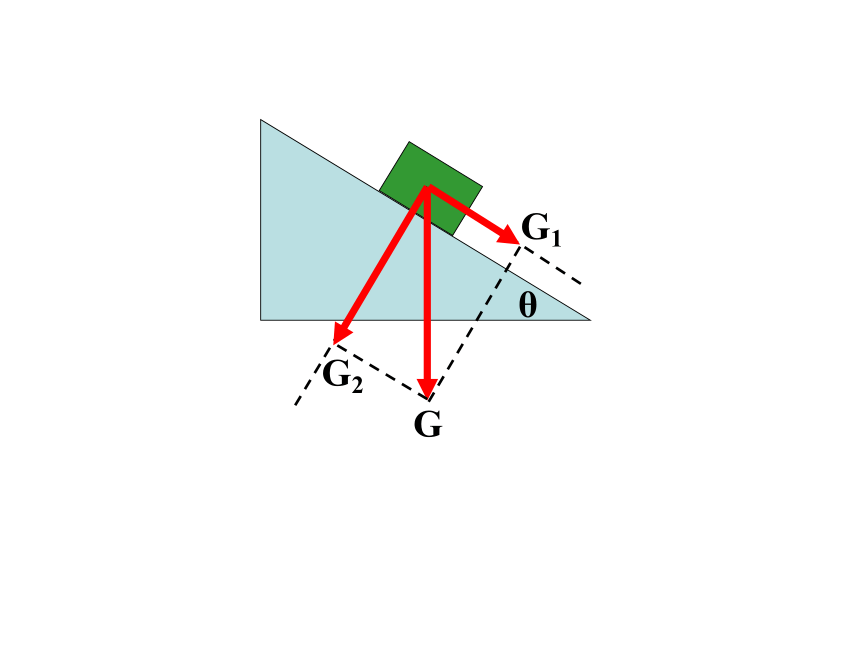
例题:倾角为θ的斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生哪些效果?应当怎样分解重力?分力的大小各是多大?
θ
G2
G1
两个分力的大小为:
分析:斜面倾角越大
G1
增大,
G2减小
G
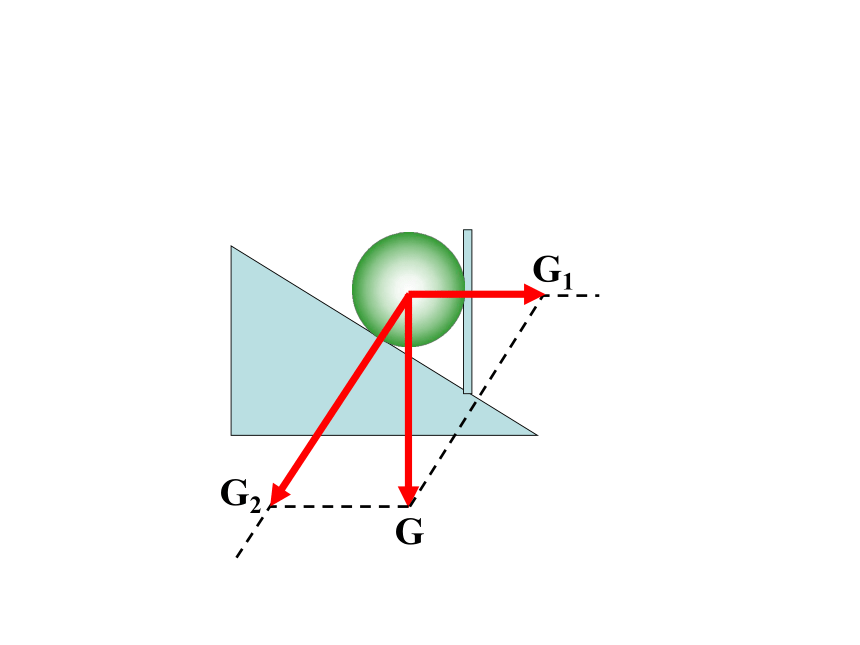
例题:如图所示,重8N的篮球用一根等于篮球半径的轻绳悬挂在竖直墙上的O点,球与墙面的接触面光滑,球的重力有哪些作用效果?按此作用效果求重力分力,则这两个分力分别是?
O
B
A
G1
G2
α=300
α=300
G2=G
tan
α
G1
=
G/
cos
α
解析提示:
总结、力的分解有唯一解的条件
2、已知合力和一个分力的大小和方向,求另一个分力的大小和方向。
1、已知合力和两个分力的方向,求两个分力的大小。
o
F
F1
F2
O
F
F1
F2
F
F
F
1
F
2
q
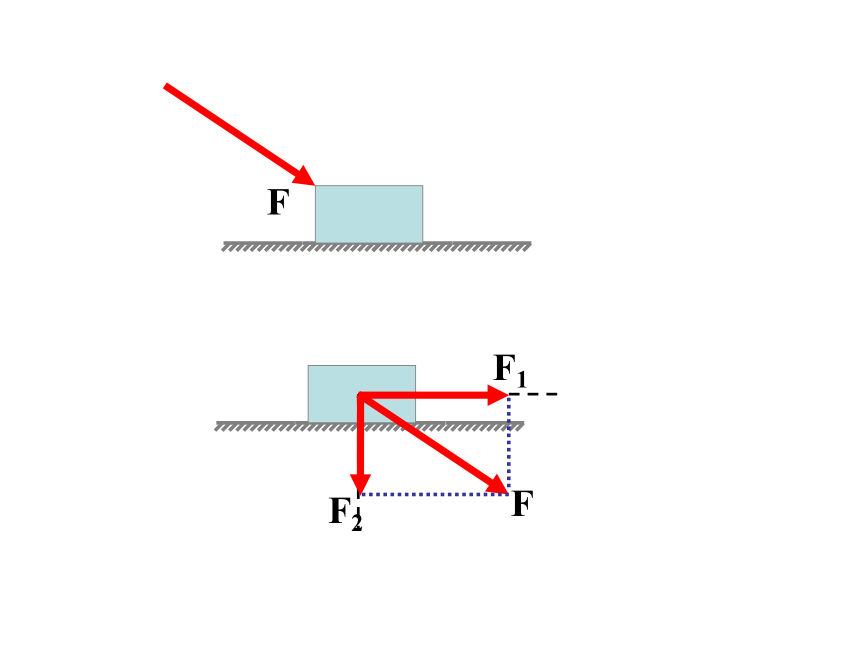
1、某人用力F
斜向上拉物体,请分析力F
产生的效果。
两个分力的大小为:
巩固练习:
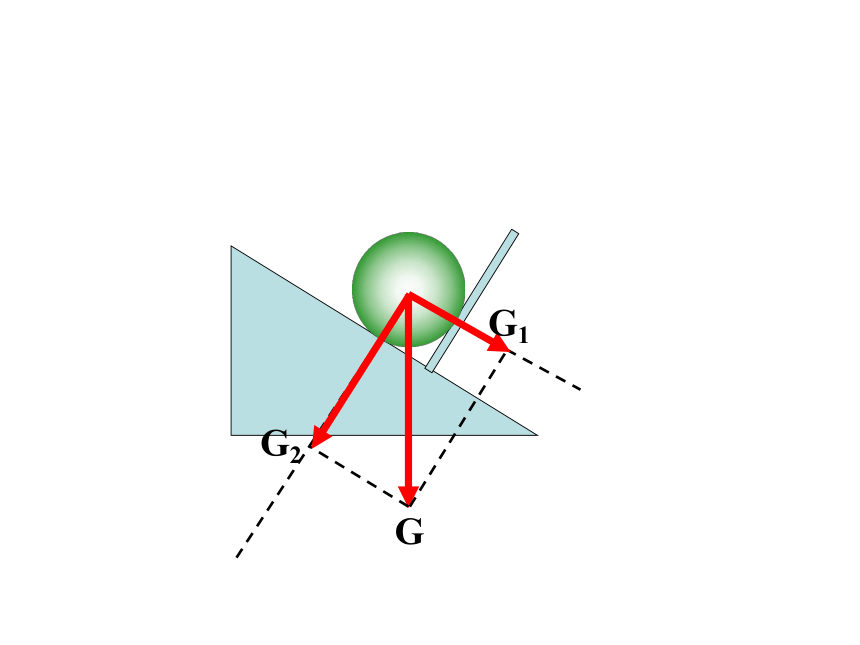
2、小球静止在斜面和挡板之间,请分解小球所受的重力。
F1/G
=
tanα
F1=G
tan
α
G/F2
=
cos
α
F2
=
G/
cos
α
α
G
α
F
1
F
2
所以,我们可以由力的作用效果来确定分力的方向。
例题:
作用在三角支架上的力,
产生怎样的作用效果?如何分解?
⊙
说明:凡是轻杆一端有铰链,起作用力就会和杆同一直线。
铰
链
x
y
o
正交分解法
F
α
Fy
Fx
用力的正交分解求多个力的合力
x
y
F
1
F
2
F
3
1、建立直角坐标系(让尽量多的力在坐标轴上,可以少分解。)
2、正交分解各力(将各力分解到两个坐标轴上)
3、分别求出x
轴和y
轴上各力的合力:
4、求出FX
和
Fy
的合力,
即为多个力的合力。
大小:
方向:
θ
Fy
Fx
F
用力的正交分解求解物体平衡问题
2、建立直角坐标系。
3、正交分解各力。(将各力分解到两个坐标轴上)
4、物体平衡时各方向上合力为零,分别写出x
方向
和y
方向方程。
5、根据方程求解。
1、画出物体的受力图。
例题:如图所示,质量为m的物体放在粗糙水平面上,它与水平面间的滑动摩擦因数为μ,在与水平面成θ角的斜向上的拉力F作用下匀速向右运动。求拉力F的大小。
θ
F
解题步骤
1、画出物体的受力图
2、建立直角坐标系
3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
例题:如图所示,质量为m的物体放在粗糙水平面上,它与水平面间的滑动摩擦因数为μ,在与水平面成θ角的斜向上的拉力F作用下匀速向右运动。求拉力F的大小。
θ
F
G
N
f
x
y
∵物体匀速运动,合外力为零
由x方向合外力为零,有:
由y方向合外力为零,有:
解得:
例题:如图所示,质量为m的物体在倾角为θ的粗糙斜面下匀速下滑,求物体与斜面间的滑动摩擦因数。
θ
解题步骤
1、画出物体的受力图
2、建立直角坐标系
3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
例题:如图所示,质量为m的物体在倾角为θ的粗糙斜面下匀速下滑,求物体与斜面间的滑动摩擦因数。
θ
mg
N
f
x
y
∵物体匀速运动,合外力为零
由x方向合外力为零,有:
由y方向合外力为零,有:
解得:
y
x
正交分解法
例题:如图,物体重力为10N,AO绳与顶板间的夹角为45?,
BO绳水平,试用计算法求出AO绳和BO绳所受拉力的大小。
A
O
B
C
FAO
FAOX
FAOY
FAOY=FAOcos45=G
FAOX=FBO=G
y
x
o
正交分解法
例题:如图,氢气球被水平吹来的风吹成图示的情形,若测得
绳子与水平面的夹角为37?,已知气球受到空气的浮力为15N,
忽略氢气球的重力,求:
①氢气球受到的水平风力多大?
②绳子对氢气球的拉力多大?
风
37?
FTsin37=15N
FTcos37=F
15N
FT
FTsin37
FTcos37
F
正交分解法
例题:如图,物体A的质量为m,斜面倾角α,A与斜面间的动
摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当
F多大时,物体A恰能沿斜面匀速向上运动?
F
FN=Fsinα+Gcosα
Fcosα=Gsinα+Ff
A
y
x
Gsinα
Gcosα
α
F
G
FN
Ff
Fsinα
Fcosα
Ff=μFN
用力的正交分解求解物体平衡问题
2、建立直角坐标系。
3、正交分解各力。(将各力分解到两个坐标轴上)
4、物体平衡时各方向上合力为零,分别写出x
方向
和y
方向方程。
5、根据方程求解。
1、画出物体的受力图。
课堂小结:
1、什么是力的分解?
2、如何进行力的分解?
3、什么是正交分解?怎样进行正交分解?
4、矢量在运算中用什么法则?
(1)按力所产生的实际作用效果进行分解。
(2)按题干要求进行分解。
(把一个已知力沿着两个互相垂直的方向进行分解)
(
平行四边形定则或三角形定则)
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
力的分解
1、力的合成
2、力的合成遵循平行四边形定则
复习引入:
力可以合成,是否也可以分解呢?
一、力的分解法则
1、力的分解是力的合成的逆运算
2、力的分解同样遵守平行四边行定则
F
F1
F2
分力F1、F2
合力F
力的合成
力的分解
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
注意:几个分力与原来那个力是等效的,它们可以互相代替,
并非同时并存!!!
F
如果没有其它限制,对于同一条对角线,可以作出无数个不同的平行四边形.
按力所产生的实际作用效果进行分解
二、确定分力原则
例如:重力
效果一:使物体沿斜面下滑
效果二:使物体紧压斜面
体会重力的作用效果
F1
F2
F3
F1
F2
F3
放在水平面上的物体受到一个斜向上的拉力F的作用,该力与水平方向夹角为θ,将力F分解。
F1=Fcos
θ F2=Fsin
θ
θ
F
F
θ
F1
F2
F
F
F1
F2
G
G2
G1
θ
G
G2
G1
G
G2
G1
F
Fa
Fb
a
b
F
F1
F2
G
θ
例题:倾角为θ的斜面上放有一个物体,如图所示。该物体受到的重力G能对物体产生哪些效果?应当怎样分解重力?分力的大小各是多大?
θ
G2
G1
两个分力的大小为:
分析:斜面倾角越大
G1
增大,
G2减小
G
例题:如图所示,重8N的篮球用一根等于篮球半径的轻绳悬挂在竖直墙上的O点,球与墙面的接触面光滑,球的重力有哪些作用效果?按此作用效果求重力分力,则这两个分力分别是?
O
B
A
G1
G2
α=300
α=300
G2=G
tan
α
G1
=
G/
cos
α
解析提示:
总结、力的分解有唯一解的条件
2、已知合力和一个分力的大小和方向,求另一个分力的大小和方向。
1、已知合力和两个分力的方向,求两个分力的大小。
o
F
F1
F2
O
F
F1
F2
F
F
F
1
F
2
q
1、某人用力F
斜向上拉物体,请分析力F
产生的效果。
两个分力的大小为:
巩固练习:
2、小球静止在斜面和挡板之间,请分解小球所受的重力。
F1/G
=
tanα
F1=G
tan
α
G/F2
=
cos
α
F2
=
G/
cos
α
α
G
α
F
1
F
2
所以,我们可以由力的作用效果来确定分力的方向。
例题:
作用在三角支架上的力,
产生怎样的作用效果?如何分解?
⊙
说明:凡是轻杆一端有铰链,起作用力就会和杆同一直线。
铰
链
x
y
o
正交分解法
F
α
Fy
Fx
用力的正交分解求多个力的合力
x
y
F
1
F
2
F
3
1、建立直角坐标系(让尽量多的力在坐标轴上,可以少分解。)
2、正交分解各力(将各力分解到两个坐标轴上)
3、分别求出x
轴和y
轴上各力的合力:
4、求出FX
和
Fy
的合力,
即为多个力的合力。
大小:
方向:
θ
Fy
Fx
F
用力的正交分解求解物体平衡问题
2、建立直角坐标系。
3、正交分解各力。(将各力分解到两个坐标轴上)
4、物体平衡时各方向上合力为零,分别写出x
方向
和y
方向方程。
5、根据方程求解。
1、画出物体的受力图。
例题:如图所示,质量为m的物体放在粗糙水平面上,它与水平面间的滑动摩擦因数为μ,在与水平面成θ角的斜向上的拉力F作用下匀速向右运动。求拉力F的大小。
θ
F
解题步骤
1、画出物体的受力图
2、建立直角坐标系
3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
例题:如图所示,质量为m的物体放在粗糙水平面上,它与水平面间的滑动摩擦因数为μ,在与水平面成θ角的斜向上的拉力F作用下匀速向右运动。求拉力F的大小。
θ
F
G
N
f
x
y
∵物体匀速运动,合外力为零
由x方向合外力为零,有:
由y方向合外力为零,有:
解得:
例题:如图所示,质量为m的物体在倾角为θ的粗糙斜面下匀速下滑,求物体与斜面间的滑动摩擦因数。
θ
解题步骤
1、画出物体的受力图
2、建立直角坐标系
3、正交分解各力
4、别写出x、y方向的方程
5、根据方程求解
例题:如图所示,质量为m的物体在倾角为θ的粗糙斜面下匀速下滑,求物体与斜面间的滑动摩擦因数。
θ
mg
N
f
x
y
∵物体匀速运动,合外力为零
由x方向合外力为零,有:
由y方向合外力为零,有:
解得:
y
x
正交分解法
例题:如图,物体重力为10N,AO绳与顶板间的夹角为45?,
BO绳水平,试用计算法求出AO绳和BO绳所受拉力的大小。
A
O
B
C
FAO
FAOX
FAOY
FAOY=FAOcos45=G
FAOX=FBO=G
y
x
o
正交分解法
例题:如图,氢气球被水平吹来的风吹成图示的情形,若测得
绳子与水平面的夹角为37?,已知气球受到空气的浮力为15N,
忽略氢气球的重力,求:
①氢气球受到的水平风力多大?
②绳子对氢气球的拉力多大?
风
37?
FTsin37=15N
FTcos37=F
15N
FT
FTsin37
FTcos37
F
正交分解法
例题:如图,物体A的质量为m,斜面倾角α,A与斜面间的动
摩擦因数为μ,斜面固定,现有一个水平力F作用在A上,当
F多大时,物体A恰能沿斜面匀速向上运动?
F
FN=Fsinα+Gcosα
Fcosα=Gsinα+Ff
A
y
x
Gsinα
Gcosα
α
F
G
FN
Ff
Fsinα
Fcosα
Ff=μFN
用力的正交分解求解物体平衡问题
2、建立直角坐标系。
3、正交分解各力。(将各力分解到两个坐标轴上)
4、物体平衡时各方向上合力为零,分别写出x
方向
和y
方向方程。
5、根据方程求解。
1、画出物体的受力图。
课堂小结:
1、什么是力的分解?
2、如何进行力的分解?
3、什么是正交分解?怎样进行正交分解?
4、矢量在运算中用什么法则?
(1)按力所产生的实际作用效果进行分解。
(2)按题干要求进行分解。
(把一个已知力沿着两个互相垂直的方向进行分解)
(
平行四边形定则或三角形定则)
把一个已知力F作为平行四边形的对角线,那么与力F共点的平行四边形的两个邻边,就表示力F的两个分力.
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
