2020-2021学年初中数学华东师大版八年级下册第17章17.2函数的图像练习题(word解析版)
文档属性
| 名称 | 2020-2021学年初中数学华东师大版八年级下册第17章17.2函数的图像练习题(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 11:32:34 | ||
图片预览



文档简介
初中数学华东师大版八年级下册第17章17.2函数的图像练习题
一、选择题
下列说法正确的是
A.
坐标轴上的点可以用一个实数表示
B.
坐标平面内的点和表示同一个点
C.
坐标平面内的点由一对有序实数唯一确定
D.
纵坐标为a,横坐标为b的点的坐标可表示成
在平面直角坐标系中,点在?
?
A.
x轴上
B.
y轴上
C.
第三象限
D.
第四象限
若点在第二象限,则点在???
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
若点在x轴上,则点在???
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
若,则点在???
A.
原点处
B.
x轴上
C.
y轴上
D.
x轴或y轴上
若点与点关于y轴对称,则???
A.
,
B.
,
C.
,
D.
,
小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离与时间的函数关系图象是
A.
B.
C.
D.
如图,在四边形ABCD中,,,,,动点M,N同时从点A出发,点M以的速度沿AB向终点B运动,点N以的速度沿折线向终点C运动.设点N的运动时间为ts,的面积为,则下列图象能大致反映S与t之间函数关系的是
A.
B.
C.
D.
如图,在边长为的等边三角形ABC中,于点D,点M,N同时从点A出发,分别沿,运动,速度都是,直到两点都到达点D即停止运动.设点M,N运动的时间为,的面积为,则y与x的函数图象大致是???
A.
B.
C.
D.
如图,和都是等边三角形,,,点A在的高DG上,点D在的高AH上,设,和的重合部分阴影部分面积记为y,则y关于x的大致图象为
A.
B.
C.
D.
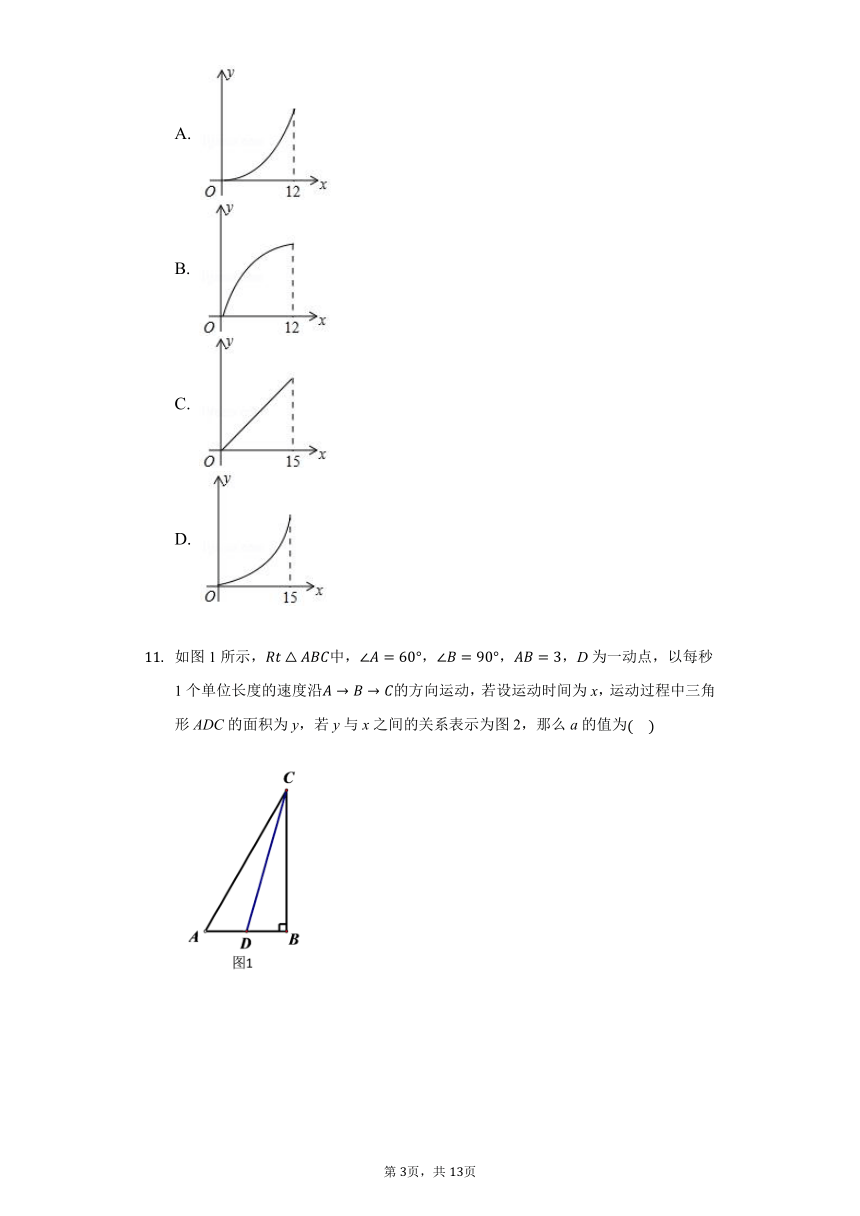
如图1所示,中,,,,D为一动点,以每秒1个单位长度的速度沿的方向运动,若设运动时间为x,运动过程中三角形ADC的面积为y,若y与x之间的关系表示为图2,那么a的值为
???
A.
B.
C.
D.
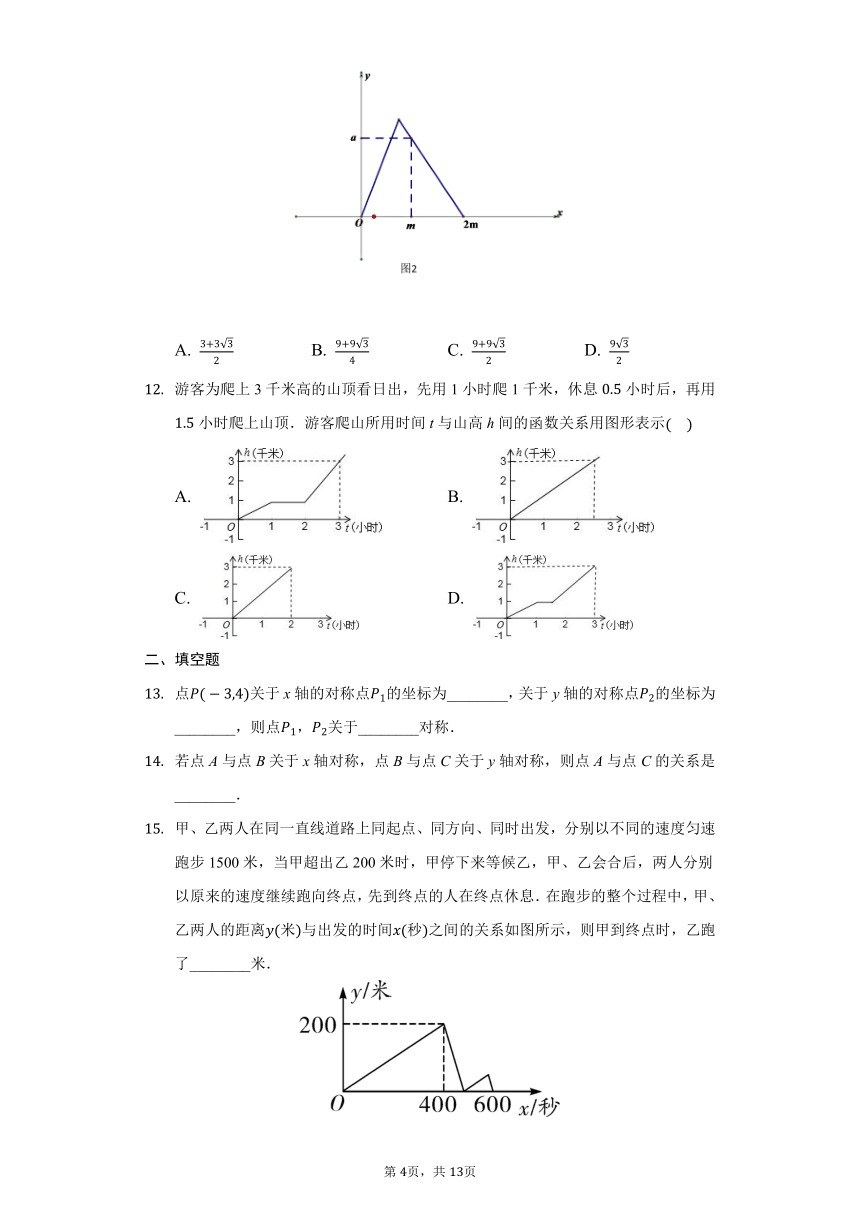
游客为爬上3千米高的山顶看日出,先用1小时爬1千米,休息小时后,再用小时爬上山顶.游客爬山所用时间t与山高h间的函数关系用图形表示
A.
B.
C.
D.
二、填空题
点关于x轴的对称点的坐标为________,关于y轴的对称点的坐标为________,则点,关于________对称.
若点A与点B关于x轴对称,点B与点C关于y轴对称,则点A与点C的关系是________.
甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息.在跑步的整个过程中,甲、乙两人的距离米与出发的时间秒之间的关系如图所示,则甲到终点时,乙跑了________米.
放学后,小明骑车回家,他行驶的路程千米与所用时间分钟的函数关系如图所示,则小明的骑车速度是___________。
三、解答题
已知点在第一象限内,且点A到x轴和y轴的距离相等,求点A的坐标.
如果点关于原点对称的点在第四象限,求m的取值范围.
小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离千米和小刘从家出发后的时间分钟之间的关系如图所示,假设二人之间交流时间忽略不计
小刘家离镇上的距离__________.
小刘和甜甜第1次相遇时离镇上距离是多少?
小刘从家里出发到回家所用的时间?
“珍重生命,注意安全”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
小明家到学校的路程是______米.
小明在书店停留了______分钟
本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
答案和解析
1.【答案】C
【解答】
解:坐标轴上的点可以用一对实数表示,故错误;
B.坐标平面内的点和表示不同的点,故错误;
C.坐标平面内的点由一对有序实数唯一确定,正确;
D.纵坐标为a,横坐标为b的点的坐标可表示成?,故错误.
故选C.
2.【答案】A
【解答】
解:由题意可知,点P横坐标不为0,纵坐标等于0,
点P在x轴上.
故选A.
3.【答案】A
【解答】
解:点在第二象限,所以,所以,,则,,
故点在第一象限.
故选A.
4.【答案】B
【解答】
解:点在x轴上,
.
,
,
点B在第二象限.
故选B.
5.【答案】D
【解答】
解:,
或,
点在x轴上或y轴上,
即点P在坐标轴上.
故选D.
6.【答案】A
【解答】
解:若点与点关于y轴对称,
y不变,x取相反值.
则,.
故选:A.
7.【答案】A
【解答】
解:他慢跑离家到江边,
随着时间的增加离家的距离越来越远,
休息了一会,
他离家的距离不变,
又后快跑回家,
他离家越来越近,直至为0,
去时慢跑,回时快跑,
小明离家的距离y与时间x的函数关系的大致图象是A.
故选:A.
8.【答案】B
解:如图1中,当时,过点M作于H.
,
如图2中,当时,连接DM,,
如图3中,当时,连接BM,,
由此可知函数图象是选项B,
故选:B.
分三种情形:如图1中,当时,如图2中,当时,如图3中,当时,分别求解即可.
本题考查动点问题的函数图象,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
9.【答案】C
【解答】
解:为正三角形,AD为高,,
,,
.
当时,;
当时;;
当时;.
故答案为C.
10.【答案】A
【解答】
解:是等边三角形,,
,,
,
,阴影部分是两个等边三角形组成的四边形,
,
点A在高DG上,所以AD最大是12,
故,
故选:A.
11.【答案】B
【解答】
解:,,,
,
,
,
解得,
当时,;
当时,
,
,
.
故选B.
12.【答案】D
【解答】
解:根据题意,先用1小时爬了1千米,是经过到的线段,
休息小时,高度不变,是平行于t轴的线段,
小时,小时,
再用小时爬上山顶是经过到的线段,
只有D选项符合.
故选:D.
13.【答案】,,原点
【解答】
解:点,则这个点关于x轴的对称点的坐标是;关于y轴的对称点的坐标是;
则点与关于原点对称.
故答案为,,原点.
14.【答案】关于原点对称
【解答】
解:若点A与点B关于x轴对称,点B与点C关于y轴对称,则点A与点C的关系是关于原点对称.
故答案为关于原点对称.
15.【答案】1450
解:乙的速度为:米秒,
甲的速度为:米秒,
甲、乙会合地离起点的距离为:米,
甲到达终点时,乙离起点的距离为:米.
故答案为:1450.
根据“速度路程时间”结合函数图象即可算出乙的速度,再根据“甲的速度乙的速度两者速度差”即可求出甲的速度,进而即可求出甲、乙会合地离起点的距离,结合总路程及二者的速度即可得出甲到终点时,乙离起点的距离,此题得解.
本题考查了函数的图象.
16.【答案】千米分钟
【解答】
解:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是千米分钟,
故答案为:千米分钟.
17.【答案】解:由题意知,
解得:,
,
.
18.【答案】解:关于原点对称的点在第四象限,
在第二象限,
点的纵坐标.
.
19.【答案】;
千米分钟,
千米,
小刘和甜甜第1次相遇时离镇上距离是千米
分钟.
答:小刘从家里出发到回家所用的时间是83分钟.
20.【答案】;
;
一共行驶的总路程
米;
共用了14分钟.
第2页,共2页
第1页,共1页
一、选择题
下列说法正确的是
A.
坐标轴上的点可以用一个实数表示
B.
坐标平面内的点和表示同一个点
C.
坐标平面内的点由一对有序实数唯一确定
D.
纵坐标为a,横坐标为b的点的坐标可表示成
在平面直角坐标系中,点在?
?
A.
x轴上
B.
y轴上
C.
第三象限
D.
第四象限
若点在第二象限,则点在???
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
若点在x轴上,则点在???
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
若,则点在???
A.
原点处
B.
x轴上
C.
y轴上
D.
x轴或y轴上
若点与点关于y轴对称,则???
A.
,
B.
,
C.
,
D.
,
小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离与时间的函数关系图象是
A.
B.
C.
D.
如图,在四边形ABCD中,,,,,动点M,N同时从点A出发,点M以的速度沿AB向终点B运动,点N以的速度沿折线向终点C运动.设点N的运动时间为ts,的面积为,则下列图象能大致反映S与t之间函数关系的是
A.
B.
C.
D.
如图,在边长为的等边三角形ABC中,于点D,点M,N同时从点A出发,分别沿,运动,速度都是,直到两点都到达点D即停止运动.设点M,N运动的时间为,的面积为,则y与x的函数图象大致是???
A.
B.
C.
D.
如图,和都是等边三角形,,,点A在的高DG上,点D在的高AH上,设,和的重合部分阴影部分面积记为y,则y关于x的大致图象为
A.
B.
C.
D.
如图1所示,中,,,,D为一动点,以每秒1个单位长度的速度沿的方向运动,若设运动时间为x,运动过程中三角形ADC的面积为y,若y与x之间的关系表示为图2,那么a的值为
???
A.
B.
C.
D.
游客为爬上3千米高的山顶看日出,先用1小时爬1千米,休息小时后,再用小时爬上山顶.游客爬山所用时间t与山高h间的函数关系用图形表示
A.
B.
C.
D.
二、填空题
点关于x轴的对称点的坐标为________,关于y轴的对称点的坐标为________,则点,关于________对称.
若点A与点B关于x轴对称,点B与点C关于y轴对称,则点A与点C的关系是________.
甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息.在跑步的整个过程中,甲、乙两人的距离米与出发的时间秒之间的关系如图所示,则甲到终点时,乙跑了________米.
放学后,小明骑车回家,他行驶的路程千米与所用时间分钟的函数关系如图所示,则小明的骑车速度是___________。
三、解答题
已知点在第一象限内,且点A到x轴和y轴的距离相等,求点A的坐标.
如果点关于原点对称的点在第四象限,求m的取值范围.
小刘从家里骑自行车出发,去镇上超市途中碰到妹妹甜甜走路从镇上回家,小刘在超市买完东西回家,在回去的路上又碰到了甜甜,便载甜甜一起回家,结果小刘比正常速度回家的时间晚了3分钟,二人离镇的距离千米和小刘从家出发后的时间分钟之间的关系如图所示,假设二人之间交流时间忽略不计
小刘家离镇上的距离__________.
小刘和甜甜第1次相遇时离镇上距离是多少?
小刘从家里出发到回家所用的时间?
“珍重生命,注意安全”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
小明家到学校的路程是______米.
小明在书店停留了______分钟
本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
答案和解析
1.【答案】C
【解答】
解:坐标轴上的点可以用一对实数表示,故错误;
B.坐标平面内的点和表示不同的点,故错误;
C.坐标平面内的点由一对有序实数唯一确定,正确;
D.纵坐标为a,横坐标为b的点的坐标可表示成?,故错误.
故选C.
2.【答案】A
【解答】
解:由题意可知,点P横坐标不为0,纵坐标等于0,
点P在x轴上.
故选A.
3.【答案】A
【解答】
解:点在第二象限,所以,所以,,则,,
故点在第一象限.
故选A.
4.【答案】B
【解答】
解:点在x轴上,
.
,
,
点B在第二象限.
故选B.
5.【答案】D
【解答】
解:,
或,
点在x轴上或y轴上,
即点P在坐标轴上.
故选D.
6.【答案】A
【解答】
解:若点与点关于y轴对称,
y不变,x取相反值.
则,.
故选:A.
7.【答案】A
【解答】
解:他慢跑离家到江边,
随着时间的增加离家的距离越来越远,
休息了一会,
他离家的距离不变,
又后快跑回家,
他离家越来越近,直至为0,
去时慢跑,回时快跑,
小明离家的距离y与时间x的函数关系的大致图象是A.
故选:A.
8.【答案】B
解:如图1中,当时,过点M作于H.
,
如图2中,当时,连接DM,,
如图3中,当时,连接BM,,
由此可知函数图象是选项B,
故选:B.
分三种情形:如图1中,当时,如图2中,当时,如图3中,当时,分别求解即可.
本题考查动点问题的函数图象,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.
9.【答案】C
【解答】
解:为正三角形,AD为高,,
,,
.
当时,;
当时;;
当时;.
故答案为C.
10.【答案】A
【解答】
解:是等边三角形,,
,,
,
,阴影部分是两个等边三角形组成的四边形,
,
点A在高DG上,所以AD最大是12,
故,
故选:A.
11.【答案】B
【解答】
解:,,,
,
,
,
解得,
当时,;
当时,
,
,
.
故选B.
12.【答案】D
【解答】
解:根据题意,先用1小时爬了1千米,是经过到的线段,
休息小时,高度不变,是平行于t轴的线段,
小时,小时,
再用小时爬上山顶是经过到的线段,
只有D选项符合.
故选:D.
13.【答案】,,原点
【解答】
解:点,则这个点关于x轴的对称点的坐标是;关于y轴的对称点的坐标是;
则点与关于原点对称.
故答案为,,原点.
14.【答案】关于原点对称
【解答】
解:若点A与点B关于x轴对称,点B与点C关于y轴对称,则点A与点C的关系是关于原点对称.
故答案为关于原点对称.
15.【答案】1450
解:乙的速度为:米秒,
甲的速度为:米秒,
甲、乙会合地离起点的距离为:米,
甲到达终点时,乙离起点的距离为:米.
故答案为:1450.
根据“速度路程时间”结合函数图象即可算出乙的速度,再根据“甲的速度乙的速度两者速度差”即可求出甲的速度,进而即可求出甲、乙会合地离起点的距离,结合总路程及二者的速度即可得出甲到终点时,乙离起点的距离,此题得解.
本题考查了函数的图象.
16.【答案】千米分钟
【解答】
解:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是千米分钟,
故答案为:千米分钟.
17.【答案】解:由题意知,
解得:,
,
.
18.【答案】解:关于原点对称的点在第四象限,
在第二象限,
点的纵坐标.
.
19.【答案】;
千米分钟,
千米,
小刘和甜甜第1次相遇时离镇上距离是千米
分钟.
答:小刘从家里出发到回家所用的时间是83分钟.
20.【答案】;
;
一共行驶的总路程
米;
共用了14分钟.
第2页,共2页
第1页,共1页
