2020-2021学年苏科版七年级下册 数学 8.2幂的乘方与积的乘方(2)课件(张PPT)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册 数学 8.2幂的乘方与积的乘方(2)课件(张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 11:34:47 | ||
图片预览







文档简介
2021
8.2 幂的乘方与积的乘方(2)
苏科版七年级下册 数学
复习回顾
1
一.知识回顾:
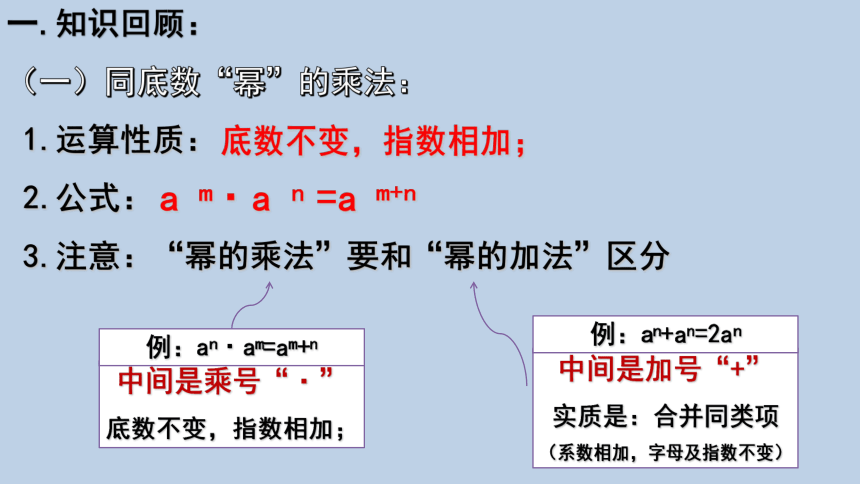
(一)同底数“幂”的乘法:
1.运算性质:
2.公式:
3.注意:“幂的乘法”要和“幂的加法”区分
底数不变,指数相加;
a m·a n =a m+n
中间是乘号“·”
底数不变,指数相加;
例:an·am=am+n
中间是加号“+”
实质是:合并同类项
(系数相加,字母及指数不变)
例:an+an=2an
一.知识回顾:
(二)“幂”的乘方:
1.运算方法:
2.公式:
3.性质:
底数不变,指数相乘;
(a m)n =a mn
(a m)n = a mn = (a n)m
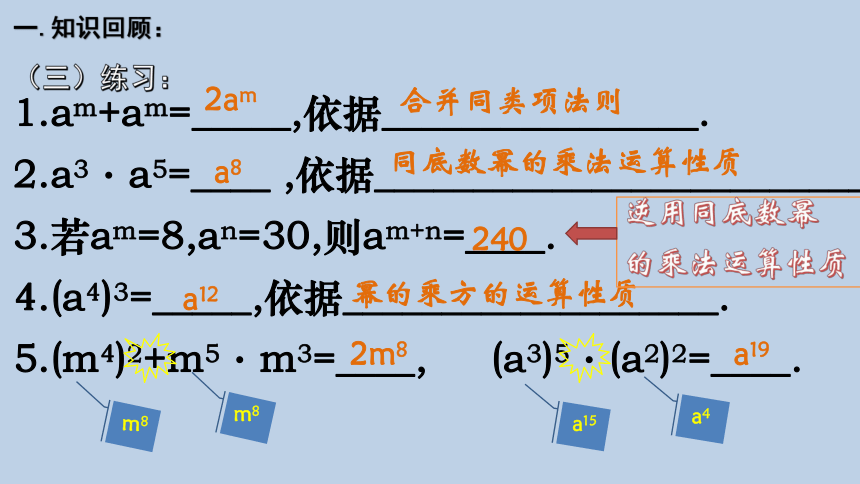
1.am+am=_____,依据________________.
2.a3·a5=____ ,依据____________________________.
3.若am=8,an=30,则am+n=____.
4.(a4)3=_____,依据___________________.
5.(m4)2+m5·m3=____, (a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂的乘法运算性质
240
a12
幂的乘方的运算性质
2m8
a19
逆用同底数幂
的乘法运算性质
m8
m8
a15
a4
一.知识回顾:
(三)练习:
探索新知
2
积的乘方:
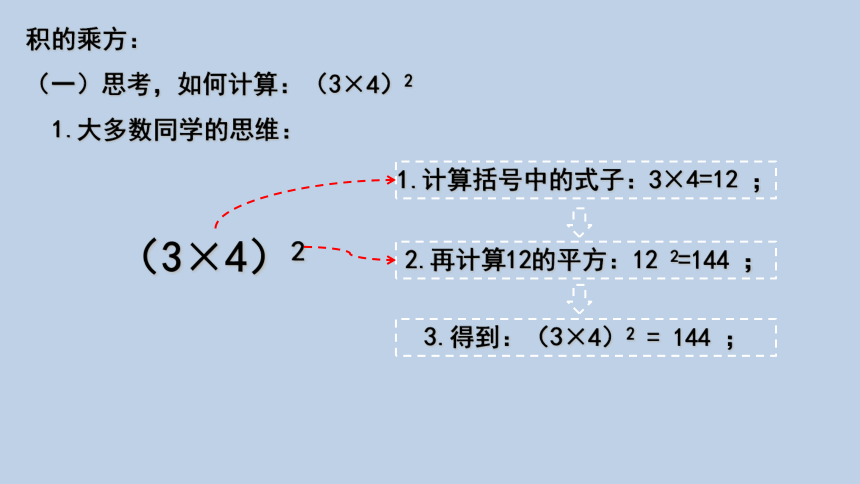
(一)思考,如何计算:(3×4)2
1.大多数同学的思维:
(3×4)2
3.得到:(3×4)2 = 144 ;
1.计算括号中的式子:3×4=12 ;
2.再计算12的平方:12 2=144 ;
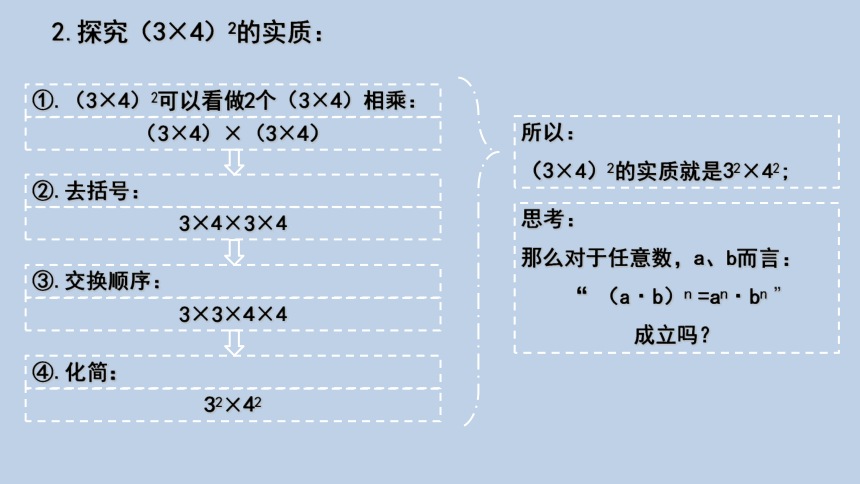
2.探究(3×4)2的实质:
①.(3×4)2可以看做2个(3×4)相乘:
(3×4)×(3×4)
②.去括号:
3×4×3×4
③.交换顺序:
3×3×4×4
④.化简:
32×42
所以:
(3×4)2的实质就是32×42;
思考:
那么对于任意数,a、b而言:
“ (a·b)n =an·bn ”
成立吗?
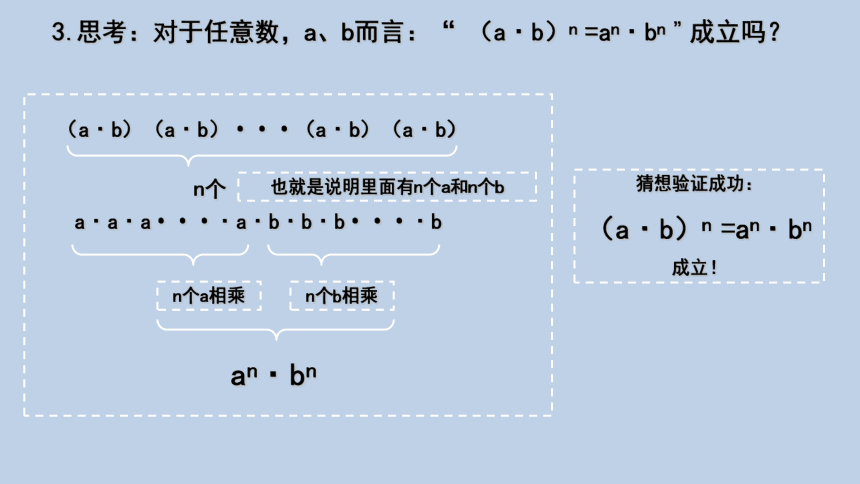
3.思考:对于任意数,a、b而言:“ (a·b)n =an·bn ”成立吗?
(a·b)(a·b)···(a·b)(a·b)
n个
也就是说明里面有n个a和n个b
a·a·a····a·b·b·b····b
n个a相乘
n个b相乘
an·bn
猜想验证成功:
(a·b)n =an·bn
成立!
4.思考:对于任意数,a、b、c而言:“ (a·b·c)n ”有什么关系?
(a·b·c)(a·b·c)···(a·b·c)(a·b·c)
n个
也就是说明里面有n个a和n个b和n个c
a·a·a····a·b·b·b····b·c·c·c····c
n个a相乘
n个b相乘
an·bn·cn
结论:(a·b·c)n =an·bn·cn
n个c相乘
积的乘方:
4.定理:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘;
即:(a·b)n =an·bn(n为正整数)
注意:
1.在运算时,一定要满足“n为正整数”;
2.(a·b)n =an·bn可以逆向运算,即:
an·bn=(a·b)n 依然成立!
推论:(a·b·c)n =an·bn·cn(n为正整数)
当n,m为正整数时
同底数幂乘法的运算性质:am · an = am+n ;
幂的乘方的运算性质: (am )n = amn;
积的乘方运算性质: (ab)n= anbn
例题讲解
3
解:⑴(5m)3
=53·m3
=125m3
(2) (-xy2)3
=(-x)3(y2)3
=-x3y6
(3) (3×103)2
=32×(103)2
=9×106
例1计算: ⑴(5m)3 (2)(-xy2)3
(3)(3×103)2 ⑷ a4.(-2a)3-(-a).(a3)2
am · an = am+n ; (am )n = amn; (ab)n= anbn
积的乘方
幂的乘方
积的乘方
幂的乘方
积的乘方
⑷ a4.(-2a)3-(-a).(a3)2
=-8a7+a7
=-7a7
同底数幂的乘法
积的乘方
合并同类项
=a4.(-8a3)+a·a6
幂的乘方
am · an = am+n ; (am )n = amn; (ab)n= anbn
例2 计算:
(3xy2)2 (2) (-2ab3c2)4
am · an = am+n ; (am )n = amn; (ab)n= anbn; (abc)n= anbncn
解:
解:
=1
你会计算吗?
试一试
(12)6 ×26
?
6个12
?
6个2
解:原式
=(12×12×…×12)×(2×2×…×2)
?
=(12×2)6
?
6个(12×2)
?
?
×
小结
一、相同底数
依据:同底数幂的乘法运算性质:am · an = am+n
二、相同指数
依据:逆用积的乘方运算性质: anbn =(ab)n
例3
变式1:
变式2:
逆用积的乘方的运算性质: anbn =(ab)n
逆用积的乘方的运算性质
逆用同底数幂乘法运算性质
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
逆用幂的乘方的运算性质amn=(am )n
变式2:
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
幂的乘方的运算性质(am )n =amn
变式2:
变式2:
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
小结
在手工课上,小军制作了一个正方体的模具,其边长是4×103㎝,问该模具的体积是多少?
解:(4×103)3
= 43×(103 )3
= 64×109
= 6.4×1010(cm3)
答:该模具的体积为6.4×1010cm3.
例4
1.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4b4 ( )
×
×
x3
4
练一练:
2.计算:
(1) a5.a3+(2a2)4 (2) (-2a)3-(-a).a2
解:原式=a8+ 2 4 a 8
=a8+16a8
= 17a8
解:原式=(-2)3 a3+ a. a2
=-8a3+a3
= -7a3
3.当2m+3n=5时,求4m.8n
解:4m.8n=(22) m .(23) n
=2 2 m . 2 3 n
= 2 2 m + 3 n
∵ 2m+3n=5
∴原式=25 =32
1.下列等式错误的是( )
A. (2mn)2=4m2n2 B. (-2mn)2=4m2n2
C. (2m2n2)3=8m6n6 D. (-2m2n2)3=-8m5n5
2.如果 ,那么m、n的值为_____________.
3.计算(-4×103)2×(-2×103)3的正确结果是( )
A. 1.28×1017 B. -1.28×1017 C. 4.8×1016 D. -1.4×1016
典型例题:
(一)“积的乘方”基础运用:
1.计算:(﹣0.25)2020×(﹣4)2019的结果是 _______________;
2.计算:(1) _______(2)-3101×(- )100=_______;
3.计算:(1) = __________(2) =___________;
4.
典型例题:
(二)“积的乘方”逆运用(指数相同或相差不大时):
1.已知 =5, =4,求 的值;
2.若 =5, =3,则 =_________;
3.若 2n=15,3n=20,则 6n=___________;
4.已知5x=m,5y=n,则52x+3y等于___________;
5.已知xm=2,xn=3,则x2m+n=___________.
典型例题:
(三)和“整体代入法”的结合:
1.已知 ,则x的值为________;
2.若m=2100,n=375,则m、n的大小关系正确的是( )
A.m>n B.m<n C.相等 D.大小关系无法确定
3.已知:84×43=2x,求x;
4.若26=a2=4b,求a+b值;
5.若2x=a,4y=b,则8x﹣4y=________.
典型例题:
(四)需要对“底数化简”的题目:
课堂小结
4
当n,m为正整数时
同底数幂乘法的运算性质:am · an = am+n ;
幂的乘方的运算性质: (am )n = amn;
积的乘方运算性质: (ab)n= anbn
(ab)n=an bn
(3×4)n=3n × 4n
(3×4)2=32×42
特殊
一般
可推广、逆用使运算简便
注意:计算时应先确定运算类型,再选择恰当运算性质。养成“以理驭算”的良好运算习惯。
8.2 幂的乘方与积的乘方(2)
苏科版七年级下册 数学
复习回顾
1
一.知识回顾:
(一)同底数“幂”的乘法:
1.运算性质:
2.公式:
3.注意:“幂的乘法”要和“幂的加法”区分
底数不变,指数相加;
a m·a n =a m+n
中间是乘号“·”
底数不变,指数相加;
例:an·am=am+n
中间是加号“+”
实质是:合并同类项
(系数相加,字母及指数不变)
例:an+an=2an
一.知识回顾:
(二)“幂”的乘方:
1.运算方法:
2.公式:
3.性质:
底数不变,指数相乘;
(a m)n =a mn
(a m)n = a mn = (a n)m
1.am+am=_____,依据________________.
2.a3·a5=____ ,依据____________________________.
3.若am=8,an=30,则am+n=____.
4.(a4)3=_____,依据___________________.
5.(m4)2+m5·m3=____, (a3)5·(a2)2=____.
2am
合并同类项法则
a8
同底数幂的乘法运算性质
240
a12
幂的乘方的运算性质
2m8
a19
逆用同底数幂
的乘法运算性质
m8
m8
a15
a4
一.知识回顾:
(三)练习:
探索新知
2
积的乘方:
(一)思考,如何计算:(3×4)2
1.大多数同学的思维:
(3×4)2
3.得到:(3×4)2 = 144 ;
1.计算括号中的式子:3×4=12 ;
2.再计算12的平方:12 2=144 ;
2.探究(3×4)2的实质:
①.(3×4)2可以看做2个(3×4)相乘:
(3×4)×(3×4)
②.去括号:
3×4×3×4
③.交换顺序:
3×3×4×4
④.化简:
32×42
所以:
(3×4)2的实质就是32×42;
思考:
那么对于任意数,a、b而言:
“ (a·b)n =an·bn ”
成立吗?
3.思考:对于任意数,a、b而言:“ (a·b)n =an·bn ”成立吗?
(a·b)(a·b)···(a·b)(a·b)
n个
也就是说明里面有n个a和n个b
a·a·a····a·b·b·b····b
n个a相乘
n个b相乘
an·bn
猜想验证成功:
(a·b)n =an·bn
成立!
4.思考:对于任意数,a、b、c而言:“ (a·b·c)n ”有什么关系?
(a·b·c)(a·b·c)···(a·b·c)(a·b·c)
n个
也就是说明里面有n个a和n个b和n个c
a·a·a····a·b·b·b····b·c·c·c····c
n个a相乘
n个b相乘
an·bn·cn
结论:(a·b·c)n =an·bn·cn
n个c相乘
积的乘方:
4.定理:
积的乘方,把积的每一个因式分别乘方,再把所得的幂相乘;
即:(a·b)n =an·bn(n为正整数)
注意:
1.在运算时,一定要满足“n为正整数”;
2.(a·b)n =an·bn可以逆向运算,即:
an·bn=(a·b)n 依然成立!
推论:(a·b·c)n =an·bn·cn(n为正整数)
当n,m为正整数时
同底数幂乘法的运算性质:am · an = am+n ;
幂的乘方的运算性质: (am )n = amn;
积的乘方运算性质: (ab)n= anbn
例题讲解
3
解:⑴(5m)3
=53·m3
=125m3
(2) (-xy2)3
=(-x)3(y2)3
=-x3y6
(3) (3×103)2
=32×(103)2
=9×106
例1计算: ⑴(5m)3 (2)(-xy2)3
(3)(3×103)2 ⑷ a4.(-2a)3-(-a).(a3)2
am · an = am+n ; (am )n = amn; (ab)n= anbn
积的乘方
幂的乘方
积的乘方
幂的乘方
积的乘方
⑷ a4.(-2a)3-(-a).(a3)2
=-8a7+a7
=-7a7
同底数幂的乘法
积的乘方
合并同类项
=a4.(-8a3)+a·a6
幂的乘方
am · an = am+n ; (am )n = amn; (ab)n= anbn
例2 计算:
(3xy2)2 (2) (-2ab3c2)4
am · an = am+n ; (am )n = amn; (ab)n= anbn; (abc)n= anbncn
解:
解:
=1
你会计算吗?
试一试
(12)6 ×26
?
6个12
?
6个2
解:原式
=(12×12×…×12)×(2×2×…×2)
?
=(12×2)6
?
6个(12×2)
?
?
×
小结
一、相同底数
依据:同底数幂的乘法运算性质:am · an = am+n
二、相同指数
依据:逆用积的乘方运算性质: anbn =(ab)n
例3
变式1:
变式2:
逆用积的乘方的运算性质: anbn =(ab)n
逆用积的乘方的运算性质
逆用同底数幂乘法运算性质
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
逆用幂的乘方的运算性质amn=(am )n
变式2:
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
幂的乘方的运算性质(am )n =amn
变式2:
变式2:
逆用同底数幂的乘法运算性质 am+n =am · an
逆用积的乘方的运算性质anbn =(ab)n
小结
在手工课上,小军制作了一个正方体的模具,其边长是4×103㎝,问该模具的体积是多少?
解:(4×103)3
= 43×(103 )3
= 64×109
= 6.4×1010(cm3)
答:该模具的体积为6.4×1010cm3.
例4
1.下面的计算是否正确?如果有错误,请改正.
(xy2)3= x y6 ( )
(-2b2)2=-4b4 ( )
×
×
x3
4
练一练:
2.计算:
(1) a5.a3+(2a2)4 (2) (-2a)3-(-a).a2
解:原式=a8+ 2 4 a 8
=a8+16a8
= 17a8
解:原式=(-2)3 a3+ a. a2
=-8a3+a3
= -7a3
3.当2m+3n=5时,求4m.8n
解:4m.8n=(22) m .(23) n
=2 2 m . 2 3 n
= 2 2 m + 3 n
∵ 2m+3n=5
∴原式=25 =32
1.下列等式错误的是( )
A. (2mn)2=4m2n2 B. (-2mn)2=4m2n2
C. (2m2n2)3=8m6n6 D. (-2m2n2)3=-8m5n5
2.如果 ,那么m、n的值为_____________.
3.计算(-4×103)2×(-2×103)3的正确结果是( )
A. 1.28×1017 B. -1.28×1017 C. 4.8×1016 D. -1.4×1016
典型例题:
(一)“积的乘方”基础运用:
1.计算:(﹣0.25)2020×(﹣4)2019的结果是 _______________;
2.计算:(1) _______(2)-3101×(- )100=_______;
3.计算:(1) = __________(2) =___________;
4.
典型例题:
(二)“积的乘方”逆运用(指数相同或相差不大时):
1.已知 =5, =4,求 的值;
2.若 =5, =3,则 =_________;
3.若 2n=15,3n=20,则 6n=___________;
4.已知5x=m,5y=n,则52x+3y等于___________;
5.已知xm=2,xn=3,则x2m+n=___________.
典型例题:
(三)和“整体代入法”的结合:
1.已知 ,则x的值为________;
2.若m=2100,n=375,则m、n的大小关系正确的是( )
A.m>n B.m<n C.相等 D.大小关系无法确定
3.已知:84×43=2x,求x;
4.若26=a2=4b,求a+b值;
5.若2x=a,4y=b,则8x﹣4y=________.
典型例题:
(四)需要对“底数化简”的题目:
课堂小结
4
当n,m为正整数时
同底数幂乘法的运算性质:am · an = am+n ;
幂的乘方的运算性质: (am )n = amn;
积的乘方运算性质: (ab)n= anbn
(ab)n=an bn
(3×4)n=3n × 4n
(3×4)2=32×42
特殊
一般
可推广、逆用使运算简便
注意:计算时应先确定运算类型,再选择恰当运算性质。养成“以理驭算”的良好运算习惯。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
