2020-2021学年七年级数学苏科版下册《第七章平面图形的认识二》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《第七章平面图形的认识二》单元测试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 248.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览



文档简介
苏科版2021年度七年级数学下册《第七章平面图形的认识二》单元综合达标测评(附答案)
1.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
2.如图,将△ABC向右平移8个单位长度得到△DEF,且点B,E,C,F在同一条直线上,若EC=4,则BC的长度是( )
A.11 B.12 C.13 D.14
3.如图,已知a∥b,在Rt△ABC中∠A=60°,∠C=90°.若∠1=50°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
4.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.45° C.60° D.64°
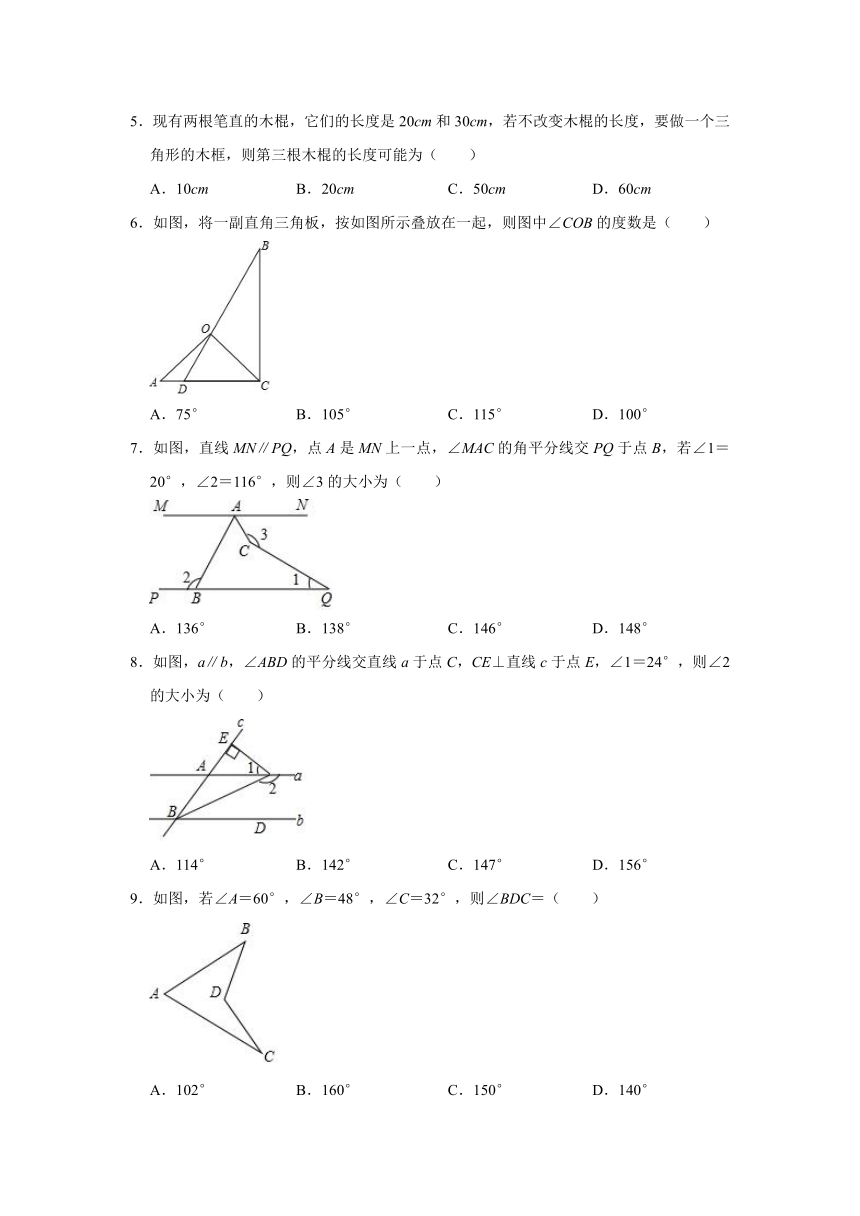
5.现有两根笔直的木棍,它们的长度是20cm和30cm,若不改变木棍的长度,要做一个三角形的木框,则第三根木棍的长度可能为( )
A.10cm B.20cm C.50cm D.60cm
6.如图,将一副直角三角板,按如图所示叠放在一起,则图中∠COB的度数是( )
A.75° B.105° C.115° D.100°
7.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
8.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
9.如图,若∠A=60°,∠B=48°,∠C=32°,则∠BDC=( )
A.102° B.160° C.150° D.140°
10.如图,在六边形ABCDEF中,∠A+∠F+∠E+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P度数为( )
A.α﹣180° B.360°﹣α C.180°﹣α D.α﹣360°
11.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
12.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为 °.
13.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
14.如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
15.如图,五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为 .
16.如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
17.将一副直角三角板按如图所示的方式放置在两平行线(l1∥l2)之间,则图中的∠1= .
18.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为 .
19.如图,BD平分∠ABC,EF∥BC,AE与BD交于点G,连接ED.若∠A=22°,∠D=20°,∠DEF=2∠AED,则∠AGB的大小= (度).
20.如图,在△ABC中,∠A=θ,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020= .(用θ表示)
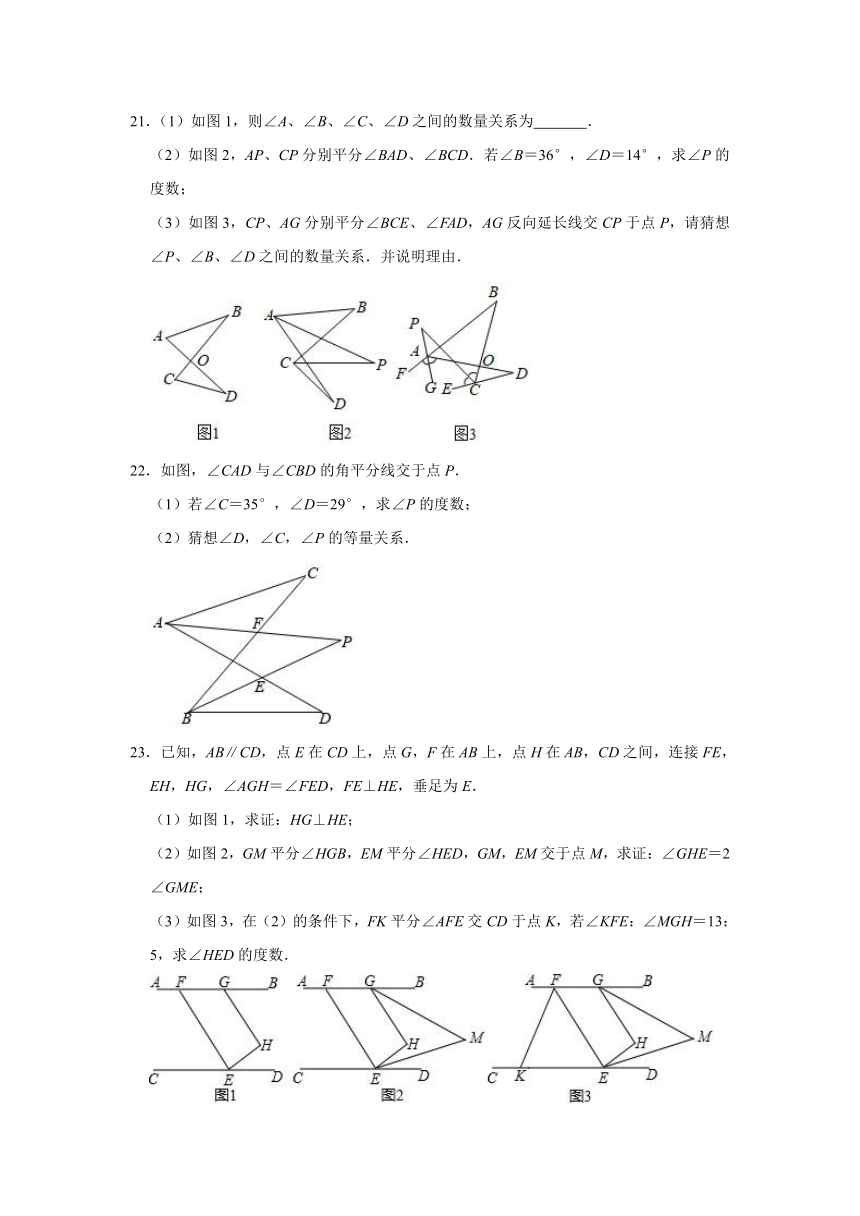
21.(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
22.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
23.已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
24.如图,在△ABC中,∠1=∠2=∠3.
(1)证明:∠BAC=∠DEF;
(2)∠BAC=70°,∠DFE=50°,求∠ABC的度数.
25.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
26.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠ABC=∠BFD;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.
参考答案
1.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
2.解:由题意,BE=CF=8,
∵EC=4,
∴BC=BE+EC=8+4=12,
故选:B.
3.解:如图,延长AC交直线b于T.
∵a∥b,
∴∠1=∠3=50°,
∴∠2=∠A+∠3=60°+50°=110°,
故选:B.
4.解:如图所示:
由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:D.
5.解:设第三根木棒的长为lcm,
∵两根笔直的木棍,它们的长度分别是20cm和30cm,
∴30cm﹣20cm<l<30cm+20cm,即10cm<l<50cm.
∴四个选项中只有B符合题意.
故选:B.
6.解:∵∠BOC=∠BDC+∠OCD,∠BDC=60°,∠OCD=45°,
∴∠BOC=105°,
故选:B.
7.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
8.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
9.解:如图,延长AD,
∵∠1=∠B+∠BAD,∠2=∠C+∠CAD,∠A=60°,∠B=48°,∠C=32°,
∴∠1+∠2=∠B+∠C+∠BAC=48°+32°+60°=140°.
故选:D.
10.解:∵∠A+∠ABC+∠BCD+∠D+∠E+∠F=(6﹣2)×180°=720°,∠A+∠F+∠E+∠D=α,
∴∠ABC+∠BCD=720°﹣α,
∵∠ABC的平分线与∠BCD的平分线交于点P,
∴∠PBC+∠PCB=,
∵∠P+∠PBC+∠PCB=180°,
∴∠P==,故选:A.
11.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
12.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
14.解:由翻折的性质可知:∠ADE=∠EDA′,∠AED=∠A′ED=(180°﹣70°)=55°,
∵∠A=55°,
∴∠ADE=∠EDA′=180°﹣55°﹣55°=70°,
∴∠A′DB=180°﹣140°=40°,
故答案为40°.
15.解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
16.解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
17.解:延长BC交直线l1于A,
∵l1∥l2,且∠ABE=60°,
∴∠BAD=180°﹣60°=120°,
∵∠BCE=90°,∠DCE=45°,
∴∠ACD=180°﹣90°﹣45°=45°,
∴∠1=180°﹣∠BAD﹣∠ACD=180°﹣45°﹣120°=15°.
故答案为:15°.
18.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
19.解:∵BD平分∠ABC,
∴∠ABD=∠DBC,
设∠ABD=x°,DE与BC交于点M,
∵∠AGB=∠DGE,
∵∠AGB=180°﹣∠A﹣∠ABD,∠DGE=180°﹣∠D﹣∠AED,
∴∠AED=x+2°,
∵∠DGE=2∠AED,
∴∠DEF=2x+4°,
∵BC∥EF,
∴∠DMC=∠DEF=2x+4°,
∵∠DMC=∠D+∠DBC,
∴2x+4°=20°+x,
解得:x=16°,
∴∠AGB=180°﹣∠A﹣∠ABD=180°﹣22°﹣16°=142°,
故答案为:142.
20.解:∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=∠ABC,∠A1CA=∠ACD,
∵∠A1CD=∠A1+∠A1BC,
∴∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD﹣∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD﹣∠ABC,
∴∠A1=∠A,
∠A2=∠A1=∠A,…,
以此类推,∠An=∠A,
∴∠A2020=∠A=.
故答案为:.
21.解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
22.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
23.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
24.(1)证明:∵∠BAC=∠1+∠CAE,∠DEF=∠3+∠CAE,∠1=∠3,
∴∠BAC=∠DEF.
(2)∵∠ABC=∠2+∠ABD,∠1=∠2,
∴∠ABC=∠1+∠ABD=∠EDF,
由(1)可知∠DEF=∠BAC=70°,
∴∠ABC=∠1+∠ABD=∠EDF=180°﹣∠DEF﹣∠DFE=180°﹣70°﹣50°=60°,
∴∠ABC=60°.
25.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
26.解:(1)∵∠BFD=∠ABF+∠BAD,∠ABC=∠ABF+∠FBC,
∵∠BAD=∠EBC,
∴∠ABC=∠BFD;
(2)∵∠BFD=∠ABC=35°,
∵EG∥AD,
∴∠BEG=∠BFD=35°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=55°
1.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
2.如图,将△ABC向右平移8个单位长度得到△DEF,且点B,E,C,F在同一条直线上,若EC=4,则BC的长度是( )
A.11 B.12 C.13 D.14
3.如图,已知a∥b,在Rt△ABC中∠A=60°,∠C=90°.若∠1=50°,则∠2的度数为( )
A.100° B.110° C.120° D.130°
4.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32° B.45° C.60° D.64°
5.现有两根笔直的木棍,它们的长度是20cm和30cm,若不改变木棍的长度,要做一个三角形的木框,则第三根木棍的长度可能为( )
A.10cm B.20cm C.50cm D.60cm
6.如图,将一副直角三角板,按如图所示叠放在一起,则图中∠COB的度数是( )
A.75° B.105° C.115° D.100°
7.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
8.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
9.如图,若∠A=60°,∠B=48°,∠C=32°,则∠BDC=( )
A.102° B.160° C.150° D.140°
10.如图,在六边形ABCDEF中,∠A+∠F+∠E+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P度数为( )
A.α﹣180° B.360°﹣α C.180°﹣α D.α﹣360°
11.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
12.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为 °.
13.如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠ACB的度数是 °.
14.如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
15.如图,五边形ABCDE中,AE∥BC,则∠C+∠D+∠E的度数为 .
16.如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1= .
17.将一副直角三角板按如图所示的方式放置在两平行线(l1∥l2)之间,则图中的∠1= .
18.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为 .
19.如图,BD平分∠ABC,EF∥BC,AE与BD交于点G,连接ED.若∠A=22°,∠D=20°,∠DEF=2∠AED,则∠AGB的大小= (度).
20.如图,在△ABC中,∠A=θ,∠ABC和∠ACD的平分线交于点A1,得∠A1,∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…;∠A2019BC和∠A2019CD的平分线交于点A2020,则∠A2020= .(用θ表示)
21.(1)如图1,则∠A、∠B、∠C、∠D之间的数量关系为 .
(2)如图2,AP、CP分别平分∠BAD、∠BCD.若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,请猜想∠P、∠B、∠D之间的数量关系.并说明理由.
22.如图,∠CAD与∠CBD的角平分线交于点P.
(1)若∠C=35°,∠D=29°,求∠P的度数;
(2)猜想∠D,∠C,∠P的等量关系.
23.已知,AB∥CD,点E在CD上,点G,F在AB上,点H在AB,CD之间,连接FE,EH,HG,∠AGH=∠FED,FE⊥HE,垂足为E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM,EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,求∠HED的度数.
24.如图,在△ABC中,∠1=∠2=∠3.
(1)证明:∠BAC=∠DEF;
(2)∠BAC=70°,∠DFE=50°,求∠ABC的度数.
25.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:∠E+∠F=90°.
26.已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明:∠ABC=∠BFD;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.
参考答案
1.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
2.解:由题意,BE=CF=8,
∵EC=4,
∴BC=BE+EC=8+4=12,
故选:B.
3.解:如图,延长AC交直线b于T.
∵a∥b,
∴∠1=∠3=50°,
∴∠2=∠A+∠3=60°+50°=110°,
故选:B.
4.解:如图所示:
由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:D.
5.解:设第三根木棒的长为lcm,
∵两根笔直的木棍,它们的长度分别是20cm和30cm,
∴30cm﹣20cm<l<30cm+20cm,即10cm<l<50cm.
∴四个选项中只有B符合题意.
故选:B.
6.解:∵∠BOC=∠BDC+∠OCD,∠BDC=60°,∠OCD=45°,
∴∠BOC=105°,
故选:B.
7.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
8.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
9.解:如图,延长AD,
∵∠1=∠B+∠BAD,∠2=∠C+∠CAD,∠A=60°,∠B=48°,∠C=32°,
∴∠1+∠2=∠B+∠C+∠BAC=48°+32°+60°=140°.
故选:D.
10.解:∵∠A+∠ABC+∠BCD+∠D+∠E+∠F=(6﹣2)×180°=720°,∠A+∠F+∠E+∠D=α,
∴∠ABC+∠BCD=720°﹣α,
∵∠ABC的平分线与∠BCD的平分线交于点P,
∴∠PBC+∠PCB=,
∵∠P+∠PBC+∠PCB=180°,
∴∠P==,故选:A.
11.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
12.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
13.解:根据三角形的外角性质,可得∠ABN=∠AOB+∠BAO,
∵BE平分∠NBA,AC平分∠BAO,
∴∠ABE=∠ABN,∠BAC=∠BAO,
∴∠C=∠ABE﹣∠BAC=(∠AOB+∠BAO)﹣∠BAO=∠AOB,
∵∠MON=90°,
∴∠AOB=90°,
∴∠C=×90°=45°.
故答案为:45.
14.解:由翻折的性质可知:∠ADE=∠EDA′,∠AED=∠A′ED=(180°﹣70°)=55°,
∵∠A=55°,
∴∠ADE=∠EDA′=180°﹣55°﹣55°=70°,
∴∠A′DB=180°﹣140°=40°,
故答案为40°.
15.解:过点D作DF∥AE,交AB于点F,
∵AE∥BC,
∴AE∥DF∥BC,
∴∠A+∠B=180°,∠E+∠EDF=180°,∠CDF+∠C=180°,
∴∠C+∠CDE+∠E=360°,
故答案为360°.
16.解:∵OP∥QR∥ST,∠2=100°,∠3=120°,
∴∠2+∠PRQ=180°,∠3=∠SRQ=120°,
∴∠PRQ=180°﹣100°=80°,
∴∠1=∠SRQ﹣∠PRQ=40°,
故答案是40°.
17.解:延长BC交直线l1于A,
∵l1∥l2,且∠ABE=60°,
∴∠BAD=180°﹣60°=120°,
∵∠BCE=90°,∠DCE=45°,
∴∠ACD=180°﹣90°﹣45°=45°,
∴∠1=180°﹣∠BAD﹣∠ACD=180°﹣45°﹣120°=15°.
故答案为:15°.
18.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
19.解:∵BD平分∠ABC,
∴∠ABD=∠DBC,
设∠ABD=x°,DE与BC交于点M,
∵∠AGB=∠DGE,
∵∠AGB=180°﹣∠A﹣∠ABD,∠DGE=180°﹣∠D﹣∠AED,
∴∠AED=x+2°,
∵∠DGE=2∠AED,
∴∠DEF=2x+4°,
∵BC∥EF,
∴∠DMC=∠DEF=2x+4°,
∵∠DMC=∠D+∠DBC,
∴2x+4°=20°+x,
解得:x=16°,
∴∠AGB=180°﹣∠A﹣∠ABD=180°﹣22°﹣16°=142°,
故答案为:142.
20.解:∵A1B平分∠ABC,A1C平分∠ACD,
∴∠A1BC=∠ABC,∠A1CA=∠ACD,
∵∠A1CD=∠A1+∠A1BC,
∴∠ACD=∠A1+∠ABC,
∴∠A1=(∠ACD﹣∠ABC),
∵∠A+∠ABC=∠ACD,
∴∠A=∠ACD﹣∠ABC,
∴∠A1=∠A,
∠A2=∠A1=∠A,…,
以此类推,∠An=∠A,
∴∠A2020=∠A=.
故答案为:.
21.解:(1)∵∠AOB+∠A+∠B=∠COD+∠C+∠D=180°,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D,
故答案为∠A+∠B=∠C+∠D;
(2)∵AP、CP分别平分∠BAD、∠BCD,
∴∠BAP=∠DAP,∠BCP=∠DCP,
由(1)可得:∠BAP+∠B=∠BCP+∠P,∠DAP+∠P=∠DCP+∠D,
∴∠B﹣∠P=∠P﹣∠D,
即2∠P=∠B+∠D,
∵∠B=36°,∠D=14°,
∴∠P=25°;
(3)2∠P=∠B+∠D.
理由:∵CP、AG分别平分∠BCE、∠FAD,
∴∠ECP=∠PCB,∠FAG=∠GAD,
∵∠PAB=∠FAG,
∴∠GAD=∠PAB,
∵∠P+∠PAB=∠B+∠PCB,
∴∠P+∠GAD=∠B+∠PCB,
∵∠P+∠PAD=∠D+∠PCD,
∴∠P+(180°﹣∠GAD)=∠D+(180°﹣∠ECP),
∴2∠P=∠B+∠D.
22.解:(1)设∠CAD=2x,∠CBD=2y,
根据∠CAD和∠CBD的角平分线相交于点P可知:
∠CAP=∠PAD=x,∠CBP=∠DBP=y,
∵三角形的内角和等于180°,∠C=35°,∠D=29°,
∴∠C+∠CAD=∠D+∠CBD,即35°+2x=29°+2y①.
∵∠AEB是△APE与△DBE的外角,
∴∠P+∠EAP=∠D+∠DBP,即∠P+x=29°+y②.
同理,∵∠AFB是△ACF与△BFP的外角,
∴∠C+∠CAP=∠P+∠CBP,即35°+x=∠P+y③,
①﹣②得,y=x+35°﹣∠P④,
①﹣③得,x=y+29°﹣∠P⑤,
④代入⑤得,x=x+35°﹣∠P+29°﹣∠P,
2∠P=35°+29°,
解得∠P=32°;
(2)∠P=(∠C+∠D),理由如下:
由(1)同理可知:
2∠P=∠C+∠D,
解得∠P=(∠C+∠D).
23.证明:(1)∵AB∥CD,
∴∠AFE=∠FED,
∵∠AGH=∠FED,
∴∠AFE=∠AGH,
∴EF∥GH,
∴∠FEH+∠H=180°,
∵FE⊥HE,
∴∠FEH=90°,
∴∠H=180°﹣∠FEH=90°,
∴HG⊥HE;
(2)过点M作MQ∥AB,
∵AB∥CD,
∴MQ∥CD,
过点H作HP∥AB,
∵AB∥CD,
∴HP∥CD,
∵GM平分∠HGB,
∴∠BGM=∠HGM=∠BGH,
∵EM平分∠HED,
∴∠HEM=∠DEM=∠HED,
∵MQ∥AB,
∴∠BGM=∠GMQ,
∵MQ∥CD,
∴∠QME=∠MED,
∴∠GME=∠GMQ+∠QME=∠BGM+∠MED,
∵HP∥AB,
∴∠BGH=∠GHP=2∠BGM,
∵HP∥CD,
∴∠PHE=∠HED=2∠MED,
∴∠GHE=∠GHP+∠PHE=2∠BGM+2∠MED=2(∠BGM+∠MED),
∴∠GHE=∠2GME;
(3)过点M作MQ∥AB,过点H作HP∥AB,
由∠KFE:∠MGH=13:5,设∠KFE=13x,∠MGH=5x,
由(2)可知:∠BGH=2∠MGH=10x,
∵∠AFE+∠BFE=180°,
∴∠AFE=180°﹣10x,
∵FK平分∠AFE,
∴∠AFK=∠KFE=∠AFE,
即,
解得:x=5°,
∴∠BGH=10x=50°,
∵HP∥AB,HP∥CD,
∴∠BGH=∠GHP=50°,∠PHE=∠HED,
∵∠GHE=90°,
∴∠PHE=∠GHE﹣∠GHP=90°﹣50°=40°,
∴∠HED=40°.
24.(1)证明:∵∠BAC=∠1+∠CAE,∠DEF=∠3+∠CAE,∠1=∠3,
∴∠BAC=∠DEF.
(2)∵∠ABC=∠2+∠ABD,∠1=∠2,
∴∠ABC=∠1+∠ABD=∠EDF,
由(1)可知∠DEF=∠BAC=70°,
∴∠ABC=∠1+∠ABD=∠EDF=180°﹣∠DEF﹣∠DFE=180°﹣70°﹣50°=60°,
∴∠ABC=60°.
25.解:(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF;
(3)∵AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE=ABC,∠BAF=∠BAD,
∴∠ABE+∠BAF=90°,
∴∠AOB=180°﹣90°=90°=∠EOF,
∴∠E+∠F=180°﹣∠EOF=90°.
26.解:(1)∵∠BFD=∠ABF+∠BAD,∠ABC=∠ABF+∠FBC,
∵∠BAD=∠EBC,
∴∠ABC=∠BFD;
(2)∵∠BFD=∠ABC=35°,
∵EG∥AD,
∴∠BEG=∠BFD=35°,
∵EH⊥BE,
∴∠BEH=90°,
∴∠HEG=∠BEH﹣∠BEG=55°
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
