北京市昌平区2020-2021学年高二上学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 北京市昌平区2020-2021学年高二上学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 685.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 21:37:10 | ||
图片预览




文档简介
北京市昌平区2020-2021学年高二上学期期末数学试题
数 学
2021.1
本试卷共6页,150分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将答题卡收回。
第一部分(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项)
(1) 已知直线false过点false和点false,则直线false的斜率为
(A)false (B)false (C)false (D)false
(2)下列命题正确的是
(A)若false,false,则false
(B)若false,false,则false
(C)若false,false,则false
(D)若false,false,则false
(3)经过点false且与直线false垂直的直线的方程为
(A)false (B)false
(C)false (D)false
(4)某高校要从经济学院的6名优秀毕业生中选3人分别到西部三个城市参加中国西部经济开发建设,要求每人去一个城市,每个城市去一人,那么不同的分配方案种数为
(A)false (B)false (C)false (D)false
(5)在空间直角坐标系falsefalse,则false的值是
(A)false (B)false (C)false (D)false
(6)小王同学在完成了高中必修课程的学习后,准备在物理、化学、生物、政治、历史、地理六门课程中选择三门来学习,他已经选择了物理,那么他选择另外两门的不同选法种数为
(A)10false(B)15 (C)20 (D)30
(7)甲、乙两个车间生产同一种产品的合格率分别为false,检验员每天都要按照false的比例分别从甲、乙两个车间抽取部分产品进行检验.从被抽检的产品中任选一件,则选到合格品的概率为
(A)false (B)false (C)false (D)false
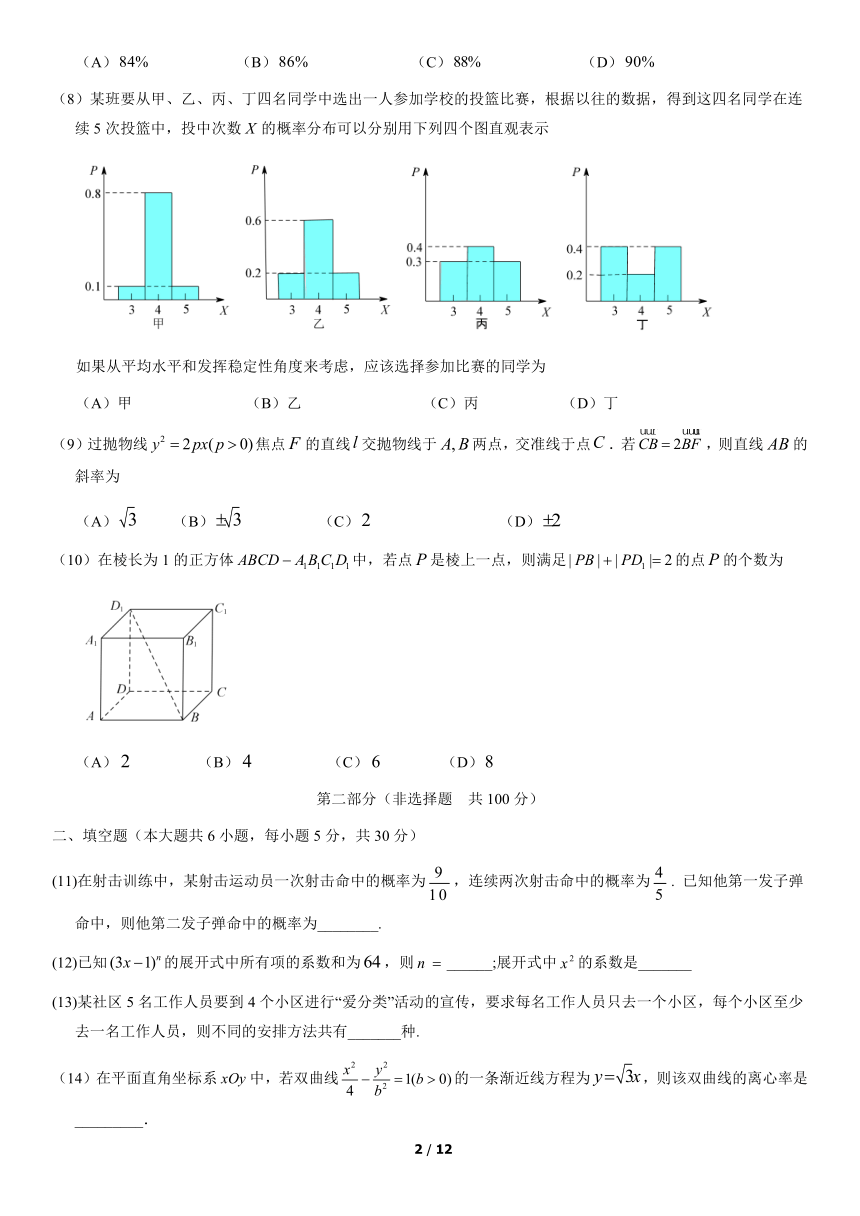
(8)某班要从甲、乙、丙、丁四名同学中选出一人参加学校的投篮比赛,根据以往的数据,得到这四名同学在连续5次投篮中,投中次数false的概率分布可以分别用下列四个图直观表示
如果从平均水平和发挥稳定性角度来考虑,应该选择参加比赛的同学为
(A)甲 (B)乙 (C)丙 (D)丁
(9)过抛物线false焦点的直线交抛物线于false两点,交准线于点.若,则直线false的斜率为
(A)false (B)false (C)false (D)false
(10)在棱长为1的正方体false中,若点false是棱上一点,则满足false的点false的个数为
(A)false (B)false (C)false (D)false
第二部分(非选择题 共100分)
二、填空题(本大题共6小题,每小题5分,共30分)
(11)在射击训练中,某射击运动员一次射击命中的概率为false,连续两次射击命中的概率为false. 已知他第一发子弹命中,则他第二发子弹命中的概率为________.
(12)已知false的展开式中所有项的系数和为false,则false______;展开式中false的系数是_______
(13)某社区5名工作人员要到4个小区进行“爱分类”活动的宣传,要求每名工作人员只去一个小区,每个小区至少去一名工作人员,则不同的安排方法共有_______种.
(14)在平面直角坐标系xOy中,若双曲线false的一条渐近线方程为false,则该双曲线的离心率是_________.
(15)已知长方体false,false.在所有的面对角线所在直线中,与平面false所成的角为false的面对角线可以是直线___________.(写出符合题意的一条直线即可)
(16)在平面直角坐标系中,动点false到两坐标轴的距离之和等于它到点false的距离.记动点false的轨迹为曲线false.给出下列四个结论:
① 曲线false关于坐标原点对称;
② 曲线false关于直线false对称;
③ 曲线false与false轴非负半轴,false轴非负半轴围成的封闭图形的面积小于false.
④ 曲线false上不存在横坐标大于1的点.
其中,所有正确结论的序号是_______.
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分14分)
已知两点false及圆false.false为经过点false的一条动直线.
(Ⅰ)若直线false经过点false,求证:直线false与圆false相切;
(II)若直线false与圆false相交于两点false从下列条件中选择一个作为已知,求false的面积.
条件①:直线false平分圆false;条件②:直线false的斜率为false.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
(18)(本小题满分14分)
已知在四棱锥false中,false平面false,
false,false,false.
(Ⅰ)求证:false;
(Ⅱ)求二面角false的余弦值;
(Ⅲ)求点false到平面false的距离.
(19)(本小题满分14分)
近年来,随着青年志愿服务活动蓬勃发展,越来越多的大学生参加到志愿服务中来,大学生志愿者已经发展成为青年志愿者队伍中最活跃、最积极、最有影响力的一个群体.大学生志愿服务的范围主要包括:帮困扶贫、支教扫盲、社区建设、环境保护、普法宣传、大型赛会、应急救助、海外服务等.为了解A,B,C,D,E,F这六所高校的大学生志愿者参加帮困扶贫的情况,从这六所高校随机抽取了部分志愿者,统计数据如下:
学校
高校A
高校B
高校C
高校D
高校E
高校F
志愿者人数
400
500
200
800
1000
600
帮困扶贫志愿者所占百分比
10%
8%
5%
12%
6%
11%
(Ⅰ)从被抽样的志愿者中任选1人,求此人是来自“高校E” 的帮困扶贫志愿者的概率;
(Ⅱ)从被抽样的来自“高校B”和“高校E” 的帮困扶贫志愿者中任选2人接受采访.
①设false为这2个志愿者中来自“高校E”的人数,求随机变量false的分布列及数学期望;
②假设表格中六所高校的帮困扶贫志愿者所占百分比均提高false,记false为这2个志愿者中来自于“高校E”的志愿者人数,试比较随机变量false的数学期望false和false的大小.(只需写出结论)
(20)(本小题满分14分)
已知在三棱柱false中,false平面false,false,且false,false,点false是false的中点.
(Ⅰ)求证:false平面false;
(Ⅱ)在棱false上是否存在一点false,使false平面false?
false若存在,指出点false的位置并证明,若不存在,说明理由.
(21)(本小题满分14分)
已知椭圆falsefalse的离心率为false设过点false的直线false交椭圆false于false,false两点.
(Ⅰ)求椭圆false的方程;
(II)若直线false的斜率为false,求false;
(III)设false为椭圆的左顶点,false分别交false轴于点false,在false轴上是否存在点false使得以false为直径的圆恒过点false?如果存在,求出点false的坐标;如果不存在,说明理由.
北京市昌平区2020-2021学年高二上学期期末数学试题
参考答案
一、选择题(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
C
D
A
B
A
B
C
二、填空题(本大题共6小题,每小题5分,共30分)
11. false 12. 6;135 13. 240 14. 2
15. false(答案不唯一) 16. ②③④
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
(17)(本小题满分14分)
解:根据题意,圆心false,半径false. ..….2分
(Ⅰ)法一:
若直线false经过点false,由false满足false,可知,点false在圆false上.
直线false的斜率false,所以false.
所以直线false与圆false相切. ..…8分
法二:若直线false经过点false,则直线false的方程为false.
圆心false到直线false的距离为false
所以直线false与圆false相切. ..…8分
(II)选择条件①:直线false平分圆false,
此时,直线false过圆心false,方程为false
点false到直线false的距离false
所以,false ..…14分
选择条件②:直线false的斜率为false,直线false的方程为false
此时,圆心false在直线false上,false
点false到直线false的距离false
所以,false ..…14分
(18)(本小题满分14分)
解:(Ⅰ)法一:因为false平面false,
false平面false,
所以false.
因为false,false,
所以false.
因为false ,
所以false平面false.
因为false平面false,
所以false. ..…5分
法二:
346837049530 因为false平面false,false平面false
所以false.
因为false,
如图建立空间直角坐标系false
则false.
(I) false
false,
所以false. ..…5分
(II) false
平面false的一个法向量为false.
设平面false的一个法向量为false,
所以false所以false.
令false,则false,所以false.
所以false.
由图知二面角false为锐角,
所以二面角false的余弦值为false. ..…10分
(Ⅲ) 设点false到平面false的距离为false,false.
由(Ⅱ)知平面false的一个法向量为false,
所以false.
所以点false到平面false的距离为false. ..…14分
(19)(本小题满分14分)
解:(Ⅰ)被抽样的志愿者共false(人),
来自“高校false” 的帮困扶贫志愿者false(人),
设“从被抽样的志愿者中任选1人,此人是来自‘高校E’的帮困扶贫志愿者”为事件false,则false. ..…5分
(Ⅱ)①被抽样的“高校false” 的帮困扶贫志愿者false(人),
被抽样的“高校false” 的帮困扶贫志愿者false(人),一共false人.
false的所有可能取值为false.
false,
false,
false.
所以随机变量false的分布列为
false
false
false
false
false
false
false
false
false.
或由false得false. ..…12分
②false. ..…14分
3587750252730(20)(本小题满分14分)
(Ⅰ)证明:法一:连接false交false于点false,连接false.
在三棱柱false中,
因为四边形false是平行四边形,
所以点false是false的中点.
因为点false是false的中点,
所以false.
因为false平面false,false平面false,
所以false平面false. ..…7分
法二:
因为false平面false,false,如图建立空间直角坐标系false,
则false,false,false ,false ,false.
所以false,false.
设平面false的一个法向量为false,则有
false.
令false得false.所以false.
所以false.
3977640220980所以false.
因为false平面false,
所以false平面false. ..…7分
(Ⅱ) 假设在棱false上存在一点false,使false平面false.
设false,则false.
由第(I)问知,平面false的法向量为false,
要使false,则false.
所以false.
解得false,即false,且false.
所以在棱false上存在一点false,且满足false,使false平面false. ..…14分
(21)(本小题满分14分)
解:(I)设椭圆false的半焦距为false根据题意,false解得false.
所以椭圆false的方程为false. ..…4分
(II) 直线false的方程false.
由false消去false,得false,即false.
解得false或false. 所以false ..…9分
(III)若满足题意的定点false存在,设false.
直线false斜率为0时,不满足题意;
设false的方程为false,
联立方程组false,化简得false.
false恒成立.
设false,false,
则false,false.
直线false的方程为false,令false,得false,
同理得false.
若以false为直径的圆恒过点false,则false,
即false,又false,false,
化简得false.
把false,false代入得false,
整理得false,得false.
所以 以false为直径的圆恒过定点false. ..…14分
法二
当直线false的斜率不存在时,直线false的方程为false,则false,false,可得false,false,
以false为直径的圆与false轴的交点为false;
所以如果以false为直径的圆过false轴上的定点,则定点只能是false;
下面进行验证定点为falsefalse.
设false的方程为false;
false,消去false得false,
false恒成立.
设false,false,
则false,false
直线false,令false,得false,
同理得:false;
只需验证:false;即false;
而false
综上,以false为直径的圆恒过点false. ..…14分
数 学
2021.1
本试卷共6页,150分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无效。考试结束后,将答题卡收回。
第一部分(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项)
(1) 已知直线false过点false和点false,则直线false的斜率为
(A)false (B)false (C)false (D)false
(2)下列命题正确的是
(A)若false,false,则false
(B)若false,false,则false
(C)若false,false,则false
(D)若false,false,则false
(3)经过点false且与直线false垂直的直线的方程为
(A)false (B)false
(C)false (D)false
(4)某高校要从经济学院的6名优秀毕业生中选3人分别到西部三个城市参加中国西部经济开发建设,要求每人去一个城市,每个城市去一人,那么不同的分配方案种数为
(A)false (B)false (C)false (D)false
(5)在空间直角坐标系falsefalse,则false的值是
(A)false (B)false (C)false (D)false
(6)小王同学在完成了高中必修课程的学习后,准备在物理、化学、生物、政治、历史、地理六门课程中选择三门来学习,他已经选择了物理,那么他选择另外两门的不同选法种数为
(A)10false(B)15 (C)20 (D)30
(7)甲、乙两个车间生产同一种产品的合格率分别为false,检验员每天都要按照false的比例分别从甲、乙两个车间抽取部分产品进行检验.从被抽检的产品中任选一件,则选到合格品的概率为
(A)false (B)false (C)false (D)false
(8)某班要从甲、乙、丙、丁四名同学中选出一人参加学校的投篮比赛,根据以往的数据,得到这四名同学在连续5次投篮中,投中次数false的概率分布可以分别用下列四个图直观表示
如果从平均水平和发挥稳定性角度来考虑,应该选择参加比赛的同学为
(A)甲 (B)乙 (C)丙 (D)丁
(9)过抛物线false焦点的直线交抛物线于false两点,交准线于点.若,则直线false的斜率为
(A)false (B)false (C)false (D)false
(10)在棱长为1的正方体false中,若点false是棱上一点,则满足false的点false的个数为
(A)false (B)false (C)false (D)false
第二部分(非选择题 共100分)
二、填空题(本大题共6小题,每小题5分,共30分)
(11)在射击训练中,某射击运动员一次射击命中的概率为false,连续两次射击命中的概率为false. 已知他第一发子弹命中,则他第二发子弹命中的概率为________.
(12)已知false的展开式中所有项的系数和为false,则false______;展开式中false的系数是_______
(13)某社区5名工作人员要到4个小区进行“爱分类”活动的宣传,要求每名工作人员只去一个小区,每个小区至少去一名工作人员,则不同的安排方法共有_______种.
(14)在平面直角坐标系xOy中,若双曲线false的一条渐近线方程为false,则该双曲线的离心率是_________.
(15)已知长方体false,false.在所有的面对角线所在直线中,与平面false所成的角为false的面对角线可以是直线___________.(写出符合题意的一条直线即可)
(16)在平面直角坐标系中,动点false到两坐标轴的距离之和等于它到点false的距离.记动点false的轨迹为曲线false.给出下列四个结论:
① 曲线false关于坐标原点对称;
② 曲线false关于直线false对称;
③ 曲线false与false轴非负半轴,false轴非负半轴围成的封闭图形的面积小于false.
④ 曲线false上不存在横坐标大于1的点.
其中,所有正确结论的序号是_______.
三、解答题(本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤)
(17)(本小题满分14分)
已知两点false及圆false.false为经过点false的一条动直线.
(Ⅰ)若直线false经过点false,求证:直线false与圆false相切;
(II)若直线false与圆false相交于两点false从下列条件中选择一个作为已知,求false的面积.
条件①:直线false平分圆false;条件②:直线false的斜率为false.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
(18)(本小题满分14分)
已知在四棱锥false中,false平面false,
false,false,false.
(Ⅰ)求证:false;
(Ⅱ)求二面角false的余弦值;
(Ⅲ)求点false到平面false的距离.
(19)(本小题满分14分)
近年来,随着青年志愿服务活动蓬勃发展,越来越多的大学生参加到志愿服务中来,大学生志愿者已经发展成为青年志愿者队伍中最活跃、最积极、最有影响力的一个群体.大学生志愿服务的范围主要包括:帮困扶贫、支教扫盲、社区建设、环境保护、普法宣传、大型赛会、应急救助、海外服务等.为了解A,B,C,D,E,F这六所高校的大学生志愿者参加帮困扶贫的情况,从这六所高校随机抽取了部分志愿者,统计数据如下:
学校
高校A
高校B
高校C
高校D
高校E
高校F
志愿者人数
400
500
200
800
1000
600
帮困扶贫志愿者所占百分比
10%
8%
5%
12%
6%
11%
(Ⅰ)从被抽样的志愿者中任选1人,求此人是来自“高校E” 的帮困扶贫志愿者的概率;
(Ⅱ)从被抽样的来自“高校B”和“高校E” 的帮困扶贫志愿者中任选2人接受采访.
①设false为这2个志愿者中来自“高校E”的人数,求随机变量false的分布列及数学期望;
②假设表格中六所高校的帮困扶贫志愿者所占百分比均提高false,记false为这2个志愿者中来自于“高校E”的志愿者人数,试比较随机变量false的数学期望false和false的大小.(只需写出结论)
(20)(本小题满分14分)
已知在三棱柱false中,false平面false,false,且false,false,点false是false的中点.
(Ⅰ)求证:false平面false;
(Ⅱ)在棱false上是否存在一点false,使false平面false?
false若存在,指出点false的位置并证明,若不存在,说明理由.
(21)(本小题满分14分)
已知椭圆falsefalse的离心率为false设过点false的直线false交椭圆false于false,false两点.
(Ⅰ)求椭圆false的方程;
(II)若直线false的斜率为false,求false;
(III)设false为椭圆的左顶点,false分别交false轴于点false,在false轴上是否存在点false使得以false为直径的圆恒过点false?如果存在,求出点false的坐标;如果不存在,说明理由.
北京市昌平区2020-2021学年高二上学期期末数学试题
参考答案
一、选择题(本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,选出符合题目要求的一项.)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
C
D
A
B
A
B
C
二、填空题(本大题共6小题,每小题5分,共30分)
11. false 12. 6;135 13. 240 14. 2
15. false(答案不唯一) 16. ②③④
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
(17)(本小题满分14分)
解:根据题意,圆心false,半径false. ..….2分
(Ⅰ)法一:
若直线false经过点false,由false满足false,可知,点false在圆false上.
直线false的斜率false,所以false.
所以直线false与圆false相切. ..…8分
法二:若直线false经过点false,则直线false的方程为false.
圆心false到直线false的距离为false
所以直线false与圆false相切. ..…8分
(II)选择条件①:直线false平分圆false,
此时,直线false过圆心false,方程为false
点false到直线false的距离false
所以,false ..…14分
选择条件②:直线false的斜率为false,直线false的方程为false
此时,圆心false在直线false上,false
点false到直线false的距离false
所以,false ..…14分
(18)(本小题满分14分)
解:(Ⅰ)法一:因为false平面false,
false平面false,
所以false.
因为false,false,
所以false.
因为false ,
所以false平面false.
因为false平面false,
所以false. ..…5分
法二:
346837049530 因为false平面false,false平面false
所以false.
因为false,
如图建立空间直角坐标系false
则false.
(I) false
false,
所以false. ..…5分
(II) false
平面false的一个法向量为false.
设平面false的一个法向量为false,
所以false所以false.
令false,则false,所以false.
所以false.
由图知二面角false为锐角,
所以二面角false的余弦值为false. ..…10分
(Ⅲ) 设点false到平面false的距离为false,false.
由(Ⅱ)知平面false的一个法向量为false,
所以false.
所以点false到平面false的距离为false. ..…14分
(19)(本小题满分14分)
解:(Ⅰ)被抽样的志愿者共false(人),
来自“高校false” 的帮困扶贫志愿者false(人),
设“从被抽样的志愿者中任选1人,此人是来自‘高校E’的帮困扶贫志愿者”为事件false,则false. ..…5分
(Ⅱ)①被抽样的“高校false” 的帮困扶贫志愿者false(人),
被抽样的“高校false” 的帮困扶贫志愿者false(人),一共false人.
false的所有可能取值为false.
false,
false,
false.
所以随机变量false的分布列为
false
false
false
false
false
false
false
false
false.
或由false得false. ..…12分
②false. ..…14分
3587750252730(20)(本小题满分14分)
(Ⅰ)证明:法一:连接false交false于点false,连接false.
在三棱柱false中,
因为四边形false是平行四边形,
所以点false是false的中点.
因为点false是false的中点,
所以false.
因为false平面false,false平面false,
所以false平面false. ..…7分
法二:
因为false平面false,false,如图建立空间直角坐标系false,
则false,false,false ,false ,false.
所以false,false.
设平面false的一个法向量为false,则有
false.
令false得false.所以false.
所以false.
3977640220980所以false.
因为false平面false,
所以false平面false. ..…7分
(Ⅱ) 假设在棱false上存在一点false,使false平面false.
设false,则false.
由第(I)问知,平面false的法向量为false,
要使false,则false.
所以false.
解得false,即false,且false.
所以在棱false上存在一点false,且满足false,使false平面false. ..…14分
(21)(本小题满分14分)
解:(I)设椭圆false的半焦距为false根据题意,false解得false.
所以椭圆false的方程为false. ..…4分
(II) 直线false的方程false.
由false消去false,得false,即false.
解得false或false. 所以false ..…9分
(III)若满足题意的定点false存在,设false.
直线false斜率为0时,不满足题意;
设false的方程为false,
联立方程组false,化简得false.
false恒成立.
设false,false,
则false,false.
直线false的方程为false,令false,得false,
同理得false.
若以false为直径的圆恒过点false,则false,
即false,又false,false,
化简得false.
把false,false代入得false,
整理得false,得false.
所以 以false为直径的圆恒过定点false. ..…14分
法二
当直线false的斜率不存在时,直线false的方程为false,则false,false,可得false,false,
以false为直径的圆与false轴的交点为false;
所以如果以false为直径的圆过false轴上的定点,则定点只能是false;
下面进行验证定点为falsefalse.
设false的方程为false;
false,消去false得false,
false恒成立.
设false,false,
则false,false
直线false,令false,得false,
同理得:false;
只需验证:false;即false;
而false
综上,以false为直径的圆恒过点false. ..…14分
同课章节目录
