广西钦州第四高级中学校2020-2021学年高一下学期第一周周测数学试题 Word版含答案
文档属性
| 名称 | 广西钦州第四高级中学校2020-2021学年高一下学期第一周周测数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 21:46:17 | ||
图片预览




文档简介
广西钦州市第四中学2021年春季学期高一数学第一周周测试卷
一.选择题
1.已知半球O与圆台OO'有公共的底面,圆台上底面圆周在半球面上,半球的半径为1,则圆台侧面积取最大值时,圆台母线与底面所成角的余弦值为( )
A. B. C. D.
2.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是2π,则该圆锥的体积为( )
A. B. C. D.
3.如图,在正四棱柱ABCD﹣A1B1C1D1中,底面边长AB=2,高A1A=4,E为棱A1A的中点,设∠BAD=α,∠BED=θ,∠B1ED=γ,则α、β、γ之间的关系正确的是( )
A.α=γ>θ B.γ>α>θ C.θ>γ>α D.α>θ>γ
4.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是该正方体棱上一点.若满足|PB|+|PC1|=m(m>0)的点的个数为4,则m的取值范围是( )
A. B. C. D.
5.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,某园林建筑为六角攒尖,它的主要部分的轮廓可近似看作一个正六棱锥,若此正六棱锥的侧面等腰三角形的底角为α,则侧棱与底面外接圆半径的比为( )
A. B. C. D.
6.已知三角形△ABC的三个内角A,B,C对应的三边分别为a,b,c,∠C=90°,分别以BC,AC,AB所在直线为旋转轴旋转一周得到的几何体的外接球表面积分别为S1,S2,S3,则下列关系正确的是( )
A.S1+S2=S3 B. C. D.
7.已知圆锥的顶点为S,底面圆心为O,以过SO的平面截该圆锥,所得截面为一个面积为4的等腰直角三角形,则该圆锥的侧面积为( )
A. B. C.8π D.16π
8.将半径为3,圆心角为的扇形作为侧面围成一个圆锥,则该圆锥的体积为( )
A.π B. C.3π D.
9.设P是△ABC所在平面α外一点,P在平面α内的射影P'在△ABC内部,且P'为△ABC的内心,则( )
A.点P到三角形的三个顶点A,B,C的距离相等
B.点P到三角形的三边AB,BC,AC的距离相等
C.点P到三角形的三边AB,BC,AC的中点的距离相等
D.三棱锥P﹣ABC为正三棱锥
10.下列说法正确的是( )
A.通过圆台侧面一点,有无数条母线
B.棱柱的底面一定是平行四边形
C.圆锥的轴截面是等腰三角形
D.用一个平面去截棱锥,原棱锥底面和截面之间的部分是棱台
11.设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,=λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,) B.[0,) C.(,1) D.(,1)
12.如图所示的组合体,其结构特征是( )
A.由两个圆锥组合成的 B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
二.填空题
13.在△ABC中,∠A=90°,AB=3,AC=4,将△ABC绕边AC所在直线旋转一周得到几何体Γ,则Γ的侧面积为 .
14.将表面积为36π的圆锥沿母线将其侧面展开,得到一个圆心角为的扇形,则该圆锥的轴截面的面积S= .
15.圆锥底面半径为lcm,母线长为2cm,则其侧面展开图扇形的圆心角θ= .
16.已知圆锥的底面半径为1,高为,则该圆锥的侧面展开图的圆心角θ的大小为 .
三.解答题
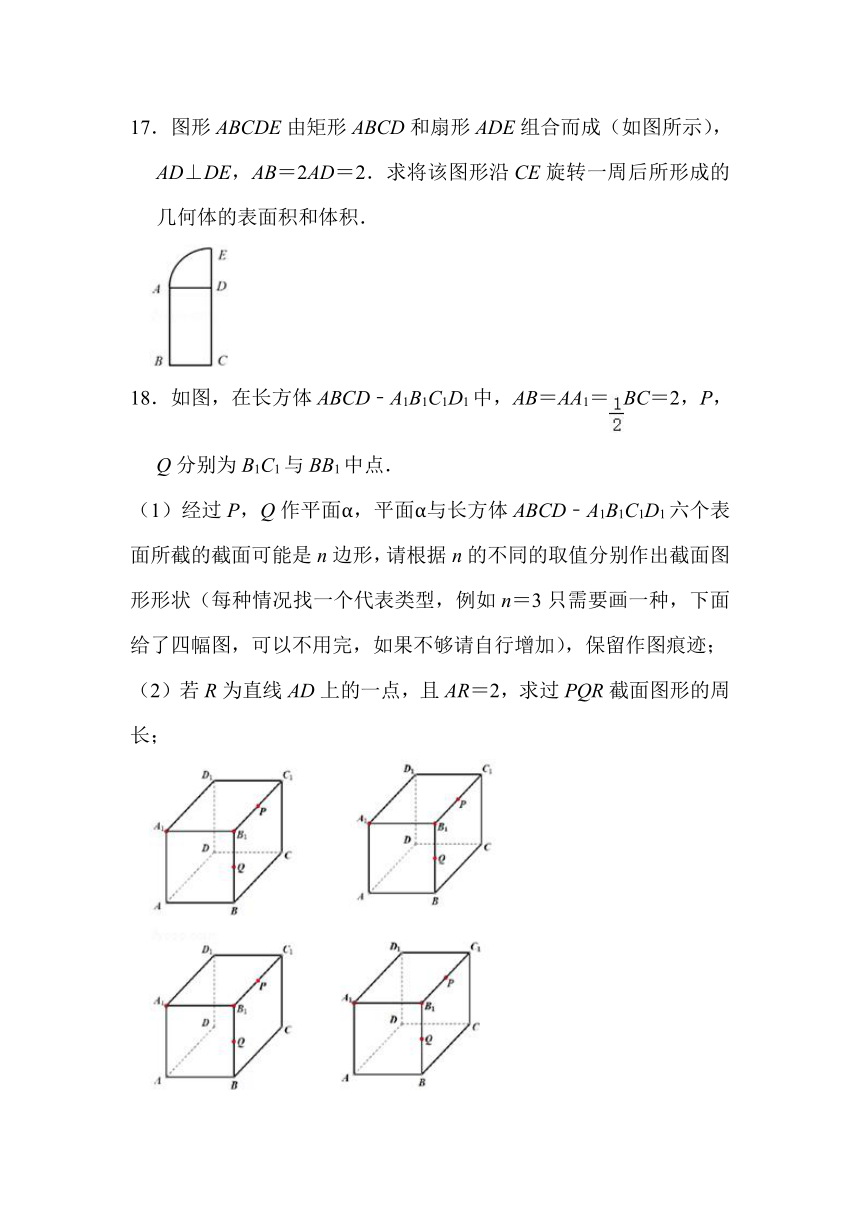
17.图形ABCDE由矩形ABCD和扇形ADE组合而成(如图所示),AD⊥DE,AB=2AD=2.求将该图形沿CE旋转一周后所形成的几何体的表面积和体积.
18.如图,在长方体ABCD﹣A1B1C1D1中,AB=AA1=BC=2,P,Q分别为B1C1与BB1中点.
(1)经过P,Q作平面α,平面α与长方体ABCD﹣A1B1C1D1六个表面所截的截面可能是n边形,请根据n的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如n=3只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
(2)若R为直线AD上的一点,且AR=2,求过PQR截面图形的周长;
19.在四棱锥P﹣ABCD中,AB∥CD,AB=2CD=2BC=2AD=4,∠DAB=60°,AE=BE,△PAD为正三角形,且平面PAD⊥平面ABCD.
(1)求二面角P﹣EC﹣D的余弦值;
(2)线段PC上是否存在一点M,使得异面直线DM和PE所成的角的余弦值为若存在,指出点M的位置;若不存在,请说明理由.
20.用一个平行于圆锥底面的平面截这个圆锥,截得圆台的上、下底面的面积之比为1:16,截去的圆锥的母线长是3cm,求圆台的母线长.
21.如图所示,在边长为6的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABD绕AD旋转一周,求阴影部分形成的几何体的表面积.
参考答案
一.选择题
1.D2.B3.B4.B5.A6.D7.A8.D9.B10.C11.A12.D
二.填空题
13.15π.14.18..15.π.16.π.
三.解答题
17.由题意得,该几何体是由一个圆柱和半球拼接而成的组合体,
其中圆柱和半球的底面半径均为1,圆柱高为2,
圆柱的底面积S1=πr2=π,
圆柱的侧面积S2=2πrh=4π,
半球球冠的表面积S3==2π,
∴将该图形沿CE旋转一周后所形成的几何体的表面积为:
S=S1+S2+S3=π+4π+2π=7π,
圆柱的体积V1=Sh=S1×2=2π,
半球的体积V2==,
∴将该图形沿CE旋转一周后所形成的几何体的体积为:
V=V1+V2=2=.
18.(1)平面α与长方体ABCD﹣A1B1C1D1表面所截的截面可能是三角形、四边形、五边形、六边形.
如图:
其中三角形时,四边形,六边形时,点均取所在棱的中点;
五边形时,G取C1D1 的四等分点(靠近C1),E为AB的四等分点(靠近B),F为CD的四等分点(靠近D).
(2)若R为直线AD上的一点,且AR=2,过PQR截面图形的周长4+2=.
19.(1)设O是AD中点,△PAD为正三角形,则PO⊥AD,平面PAD⊥平面ABCD,
PO⊥平面ABCD,又AD=AE=2,∠DAB=60°,∴△ADE为正三角形,OE⊥AD,
以O为原点,OA为x轴,OE为y轴,OP为z轴,建立空间直角坐标系,如图,
则P(0,0,),E(0,,0),C(﹣2,,0),
设平面PEC法向量为=(x,y,z),=(﹣2,,﹣),=(0,,﹣),
则,取y=1,得=(0,1,1),
平面EDC的法向量=(0,0,1),
cos<,>==,
∴二面角P﹣EC﹣D的余弦值为.
(2)设,则,
=,,
所以===,
所以或,所以存在点M为线段PC的三等分点.
20.设圆台的上下底面半径为别为r,R,圆台母线长为l,
∴=,∴∴=,解得l=9 (cm).
21.所形成几何体是一个圆锥挖去一个圆柱,
由题意可知圆柱的底面半径为,高为,圆锥底面半径为3,母线为6,
所以S圆柱侧=2π××=,S圆锥表=π×32+π×3×6=27π,
一.选择题
1.已知半球O与圆台OO'有公共的底面,圆台上底面圆周在半球面上,半球的半径为1,则圆台侧面积取最大值时,圆台母线与底面所成角的余弦值为( )
A. B. C. D.
2.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是2π,则该圆锥的体积为( )
A. B. C. D.
3.如图,在正四棱柱ABCD﹣A1B1C1D1中,底面边长AB=2,高A1A=4,E为棱A1A的中点,设∠BAD=α,∠BED=θ,∠B1ED=γ,则α、β、γ之间的关系正确的是( )
A.α=γ>θ B.γ>α>θ C.θ>γ>α D.α>θ>γ
4.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是该正方体棱上一点.若满足|PB|+|PC1|=m(m>0)的点的个数为4,则m的取值范围是( )
A. B. C. D.
5.攒尖是古代中国建筑中屋顶的一种结构形式.宋代称为撮尖,清代称攒尖.依其平面有圆形攒尖、三角攒尖、四角攒尖、六角攒尖等,也有单檐和重檐之分,多见于亭阁式建筑.如图所示,某园林建筑为六角攒尖,它的主要部分的轮廓可近似看作一个正六棱锥,若此正六棱锥的侧面等腰三角形的底角为α,则侧棱与底面外接圆半径的比为( )
A. B. C. D.
6.已知三角形△ABC的三个内角A,B,C对应的三边分别为a,b,c,∠C=90°,分别以BC,AC,AB所在直线为旋转轴旋转一周得到的几何体的外接球表面积分别为S1,S2,S3,则下列关系正确的是( )
A.S1+S2=S3 B. C. D.
7.已知圆锥的顶点为S,底面圆心为O,以过SO的平面截该圆锥,所得截面为一个面积为4的等腰直角三角形,则该圆锥的侧面积为( )
A. B. C.8π D.16π
8.将半径为3,圆心角为的扇形作为侧面围成一个圆锥,则该圆锥的体积为( )
A.π B. C.3π D.
9.设P是△ABC所在平面α外一点,P在平面α内的射影P'在△ABC内部,且P'为△ABC的内心,则( )
A.点P到三角形的三个顶点A,B,C的距离相等
B.点P到三角形的三边AB,BC,AC的距离相等
C.点P到三角形的三边AB,BC,AC的中点的距离相等
D.三棱锥P﹣ABC为正三棱锥
10.下列说法正确的是( )
A.通过圆台侧面一点,有无数条母线
B.棱柱的底面一定是平行四边形
C.圆锥的轴截面是等腰三角形
D.用一个平面去截棱锥,原棱锥底面和截面之间的部分是棱台
11.设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上,=λ,当∠APC为锐角时,λ的取值范围是( )
A.[0,) B.[0,) C.(,1) D.(,1)
12.如图所示的组合体,其结构特征是( )
A.由两个圆锥组合成的 B.由两个圆柱组合成的
C.由一个棱锥和一个棱柱组合成的
D.由一个圆锥和一个圆柱组合成的
二.填空题
13.在△ABC中,∠A=90°,AB=3,AC=4,将△ABC绕边AC所在直线旋转一周得到几何体Γ,则Γ的侧面积为 .
14.将表面积为36π的圆锥沿母线将其侧面展开,得到一个圆心角为的扇形,则该圆锥的轴截面的面积S= .
15.圆锥底面半径为lcm,母线长为2cm,则其侧面展开图扇形的圆心角θ= .
16.已知圆锥的底面半径为1,高为,则该圆锥的侧面展开图的圆心角θ的大小为 .
三.解答题
17.图形ABCDE由矩形ABCD和扇形ADE组合而成(如图所示),AD⊥DE,AB=2AD=2.求将该图形沿CE旋转一周后所形成的几何体的表面积和体积.
18.如图,在长方体ABCD﹣A1B1C1D1中,AB=AA1=BC=2,P,Q分别为B1C1与BB1中点.
(1)经过P,Q作平面α,平面α与长方体ABCD﹣A1B1C1D1六个表面所截的截面可能是n边形,请根据n的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如n=3只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;
(2)若R为直线AD上的一点,且AR=2,求过PQR截面图形的周长;
19.在四棱锥P﹣ABCD中,AB∥CD,AB=2CD=2BC=2AD=4,∠DAB=60°,AE=BE,△PAD为正三角形,且平面PAD⊥平面ABCD.
(1)求二面角P﹣EC﹣D的余弦值;
(2)线段PC上是否存在一点M,使得异面直线DM和PE所成的角的余弦值为若存在,指出点M的位置;若不存在,请说明理由.
20.用一个平行于圆锥底面的平面截这个圆锥,截得圆台的上、下底面的面积之比为1:16,截去的圆锥的母线长是3cm,求圆台的母线长.
21.如图所示,在边长为6的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABD绕AD旋转一周,求阴影部分形成的几何体的表面积.
参考答案
一.选择题
1.D2.B3.B4.B5.A6.D7.A8.D9.B10.C11.A12.D
二.填空题
13.15π.14.18..15.π.16.π.
三.解答题
17.由题意得,该几何体是由一个圆柱和半球拼接而成的组合体,
其中圆柱和半球的底面半径均为1,圆柱高为2,
圆柱的底面积S1=πr2=π,
圆柱的侧面积S2=2πrh=4π,
半球球冠的表面积S3==2π,
∴将该图形沿CE旋转一周后所形成的几何体的表面积为:
S=S1+S2+S3=π+4π+2π=7π,
圆柱的体积V1=Sh=S1×2=2π,
半球的体积V2==,
∴将该图形沿CE旋转一周后所形成的几何体的体积为:
V=V1+V2=2=.
18.(1)平面α与长方体ABCD﹣A1B1C1D1表面所截的截面可能是三角形、四边形、五边形、六边形.
如图:
其中三角形时,四边形,六边形时,点均取所在棱的中点;
五边形时,G取C1D1 的四等分点(靠近C1),E为AB的四等分点(靠近B),F为CD的四等分点(靠近D).
(2)若R为直线AD上的一点,且AR=2,过PQR截面图形的周长4+2=.
19.(1)设O是AD中点,△PAD为正三角形,则PO⊥AD,平面PAD⊥平面ABCD,
PO⊥平面ABCD,又AD=AE=2,∠DAB=60°,∴△ADE为正三角形,OE⊥AD,
以O为原点,OA为x轴,OE为y轴,OP为z轴,建立空间直角坐标系,如图,
则P(0,0,),E(0,,0),C(﹣2,,0),
设平面PEC法向量为=(x,y,z),=(﹣2,,﹣),=(0,,﹣),
则,取y=1,得=(0,1,1),
平面EDC的法向量=(0,0,1),
cos<,>==,
∴二面角P﹣EC﹣D的余弦值为.
(2)设,则,
=,,
所以===,
所以或,所以存在点M为线段PC的三等分点.
20.设圆台的上下底面半径为别为r,R,圆台母线长为l,
∴=,∴∴=,解得l=9 (cm).
21.所形成几何体是一个圆锥挖去一个圆柱,
由题意可知圆柱的底面半径为,高为,圆锥底面半径为3,母线为6,
所以S圆柱侧=2π××=,S圆锥表=π×32+π×3×6=27π,
同课章节目录
