苏科版七上 4.2解一元一次方程 课件2
文档属性
| 名称 | 苏科版七上 4.2解一元一次方程 课件2 |  | |
| 格式 | rar | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-05 15:05:55 | ||
图片预览



文档简介
(共14张PPT)
韶关市第十一中学
刘迎春
(1)把天平放在水平的位置,取下胶垫;
天平的使用方法
(2)调平;
游码靠0刻度,调整天平右边的螺丝,使天平处于平衡状态(指针静止在正中刻度)
(3)被称物体放在天平的左盘,砝码放在右盘;
注意
砝码必须使用镊子轻取轻放,天平不得称其它质量大的物体以免损坏!
(1)砝码质量(5g,10g,20g,50g,100g)
天平的读数
(2)游码(0g-5g,每小格表示0.2g)
天平的读数=砝码质量+游码表示质量
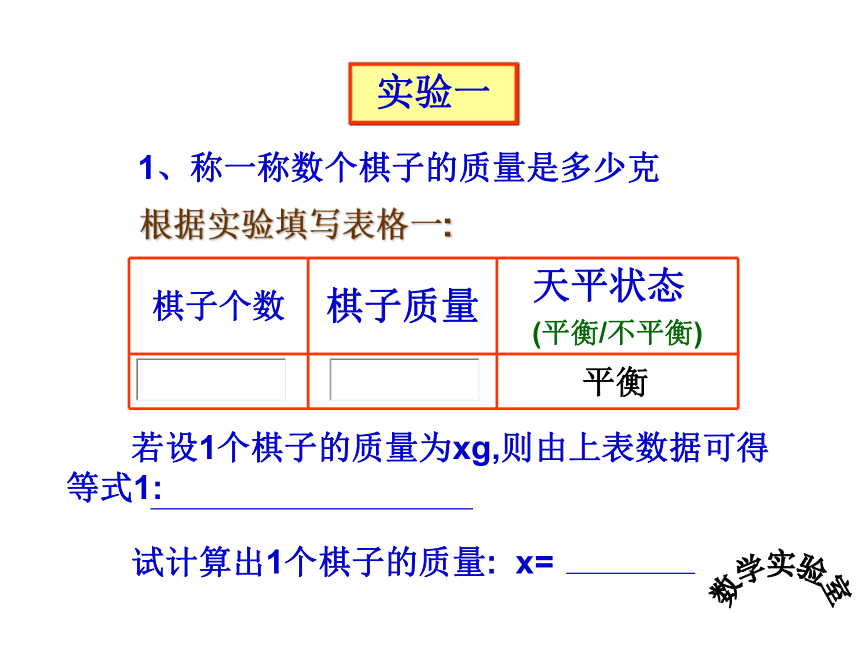
实验一
棋子个数 棋子质量 天平状态
(平衡/不平衡)
若设1个棋子的质量为xg,则由上表数据可得等式1:
试计算出1个棋子的质量: x=
根据实验填写表格一:
1、称一称数个棋子的质量是多少克
平衡
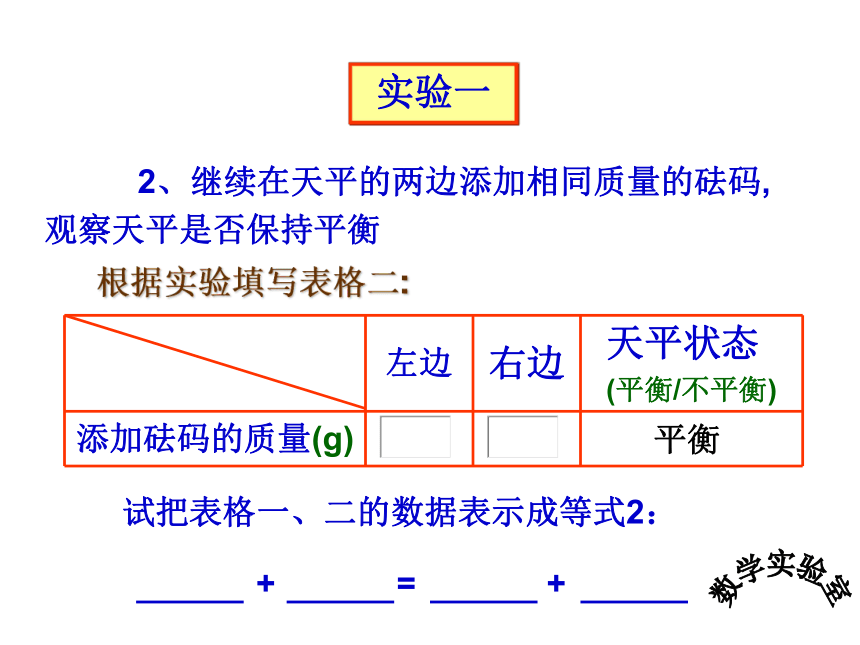
2、继续在天平的两边添加相同质量的砝码,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
添加砝码的质量(g)
试把表格一、二的数据表示成等式2:
+ = +
根据实验填写表格二:
实验一
平衡
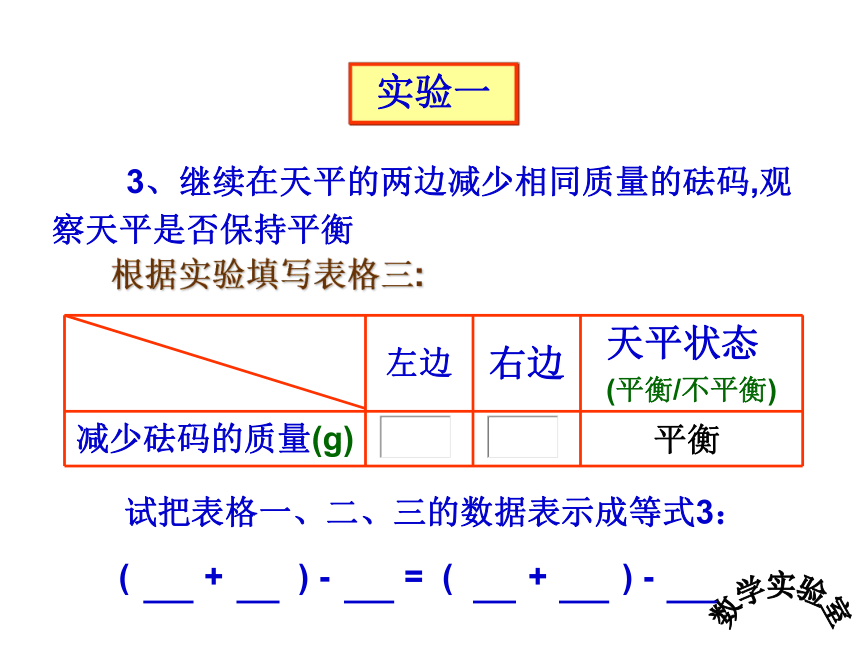
3、继续在天平的两边减少相同质量的砝码,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
减少砝码的质量(g)
试把表格一、二、三的数据表示成等式3:
根据实验填写表格三:
( + ) - = ( + ) -
实验一
平衡
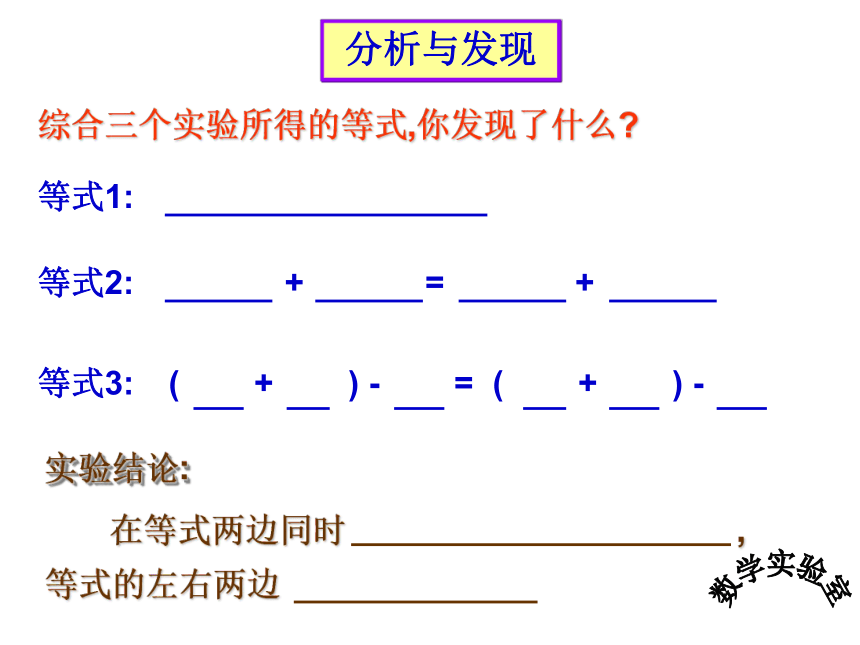
分析与发现
实验结论:
等式1:
+ = +
等式2:
( + ) - = ( + ) -
等式3:
综合三个实验所得的等式,你发现了什么
在等式两边同时 ,
等式的左右两边
1、在天平左右两边放相同质量的砝码,观察天平是否保持平衡
实验二
2、把天平两边所放砝码的质量同时扩大相同的倍数观察天平是否保持平衡
3、把天平两边所放砝码的质量同时缩小为原来质量的几分之几,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
原有砝码的质量(g)
扩大 倍后砝码质量(g)
缩小为 分之 后砝码质量(g)
根据实验填写表格四:
实验结论:
在等式两边同时 ,
等式的左右两边
平衡
平衡
平衡
实验二
等式的基本性质1:
等式的基本性质2:
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式。
课本P119
分析与发现
以下解方程中分别运用了等式的哪些基本性质?
① x + 2 = 1
② 3x = - 6
x + 2 – 2 = 1 - 2
x = -1
解:方程两边同时减去2,
x = -2
解:方程两边同时除以3,
=
3x
3
- 6
3
(等式的基本性质1)
求方程的解的过程叫做解方程
(等式的基本性质1)
尝试与应用
利用等式的基本性质求下列方程中x的值:
③ x - 4 = -7
④ -2x = 8
x - 4 +4 = -7 +4
x = - 3
解:方程两边同时加上4,
x = - 4
解:方程两边同时除以-2,
=
-2x
-2
8
-2
你有办法检验计算的结果是否正确吗?
把 x = - 3分别代入原方程的左边和右边:
左边= - 3 - 4= - 7
右边= - 7
因为左边=右边
所以 x = - 3是原方程的解
能使方程左右两边相等的未知数的值,叫做方程的解
☆你理解吗?
等式的基本性质……
☆你知道吗?
什么是方程的解?
如何判断一个未知数的值是不是某个方程的解?
☆你想过吗?
什么情况适合运用等式的基本性质1解方程?等式的基本性质2呢?
作业
课本p120《练一练》
第1题
韶关市第十一中学
刘迎春
(1)把天平放在水平的位置,取下胶垫;
天平的使用方法
(2)调平;
游码靠0刻度,调整天平右边的螺丝,使天平处于平衡状态(指针静止在正中刻度)
(3)被称物体放在天平的左盘,砝码放在右盘;
注意
砝码必须使用镊子轻取轻放,天平不得称其它质量大的物体以免损坏!
(1)砝码质量(5g,10g,20g,50g,100g)
天平的读数
(2)游码(0g-5g,每小格表示0.2g)
天平的读数=砝码质量+游码表示质量
实验一
棋子个数 棋子质量 天平状态
(平衡/不平衡)
若设1个棋子的质量为xg,则由上表数据可得等式1:
试计算出1个棋子的质量: x=
根据实验填写表格一:
1、称一称数个棋子的质量是多少克
平衡
2、继续在天平的两边添加相同质量的砝码,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
添加砝码的质量(g)
试把表格一、二的数据表示成等式2:
+ = +
根据实验填写表格二:
实验一
平衡
3、继续在天平的两边减少相同质量的砝码,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
减少砝码的质量(g)
试把表格一、二、三的数据表示成等式3:
根据实验填写表格三:
( + ) - = ( + ) -
实验一
平衡
分析与发现
实验结论:
等式1:
+ = +
等式2:
( + ) - = ( + ) -
等式3:
综合三个实验所得的等式,你发现了什么
在等式两边同时 ,
等式的左右两边
1、在天平左右两边放相同质量的砝码,观察天平是否保持平衡
实验二
2、把天平两边所放砝码的质量同时扩大相同的倍数观察天平是否保持平衡
3、把天平两边所放砝码的质量同时缩小为原来质量的几分之几,观察天平是否保持平衡
左边 右边 天平状态
(平衡/不平衡)
原有砝码的质量(g)
扩大 倍后砝码质量(g)
缩小为 分之 后砝码质量(g)
根据实验填写表格四:
实验结论:
在等式两边同时 ,
等式的左右两边
平衡
平衡
平衡
实验二
等式的基本性质1:
等式的基本性质2:
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
等式两边都乘以(或除以)同一个不等于0的数,所得结果仍是等式。
课本P119
分析与发现
以下解方程中分别运用了等式的哪些基本性质?
① x + 2 = 1
② 3x = - 6
x + 2 – 2 = 1 - 2
x = -1
解:方程两边同时减去2,
x = -2
解:方程两边同时除以3,
=
3x
3
- 6
3
(等式的基本性质1)
求方程的解的过程叫做解方程
(等式的基本性质1)
尝试与应用
利用等式的基本性质求下列方程中x的值:
③ x - 4 = -7
④ -2x = 8
x - 4 +4 = -7 +4
x = - 3
解:方程两边同时加上4,
x = - 4
解:方程两边同时除以-2,
=
-2x
-2
8
-2
你有办法检验计算的结果是否正确吗?
把 x = - 3分别代入原方程的左边和右边:
左边= - 3 - 4= - 7
右边= - 7
因为左边=右边
所以 x = - 3是原方程的解
能使方程左右两边相等的未知数的值,叫做方程的解
☆你理解吗?
等式的基本性质……
☆你知道吗?
什么是方程的解?
如何判断一个未知数的值是不是某个方程的解?
☆你想过吗?
什么情况适合运用等式的基本性质1解方程?等式的基本性质2呢?
作业
课本p120《练一练》
第1题
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
