2020-2021学年人教版数学七年级下册 5.3.1 平行线的性质 课件(21张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册 5.3.1 平行线的性质 课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 18:17:25 | ||
图片预览






文档简介
5.3.1 平行线的性质
人教版数学七年级下册
第五章 相交线与平行线
2. 能够根据平行线的性质进行简单的推理.(难点)
2
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)
1
判定方法1 同位角相等, 两直线平行.
判定方法2 内错角相等, 两直线平行.
判定方法3 同旁内角互补,两直线平行.
结 论
平行线的判定
新课导入
条件
两
直
线
平
行
条 件
结 论
?
两条平行线
被第三条直
线所截
同位角?
内错角?
同旁内角?
条 件
结 论
思考
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
核心知识点一
平行线的基本性质1
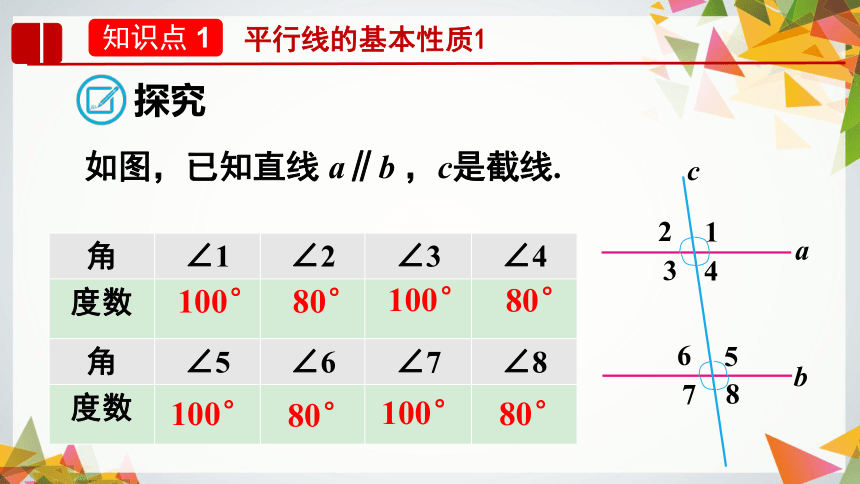
如图,已知直线 a∥b ,c是截线.
b
a
c
1
2
3
4
5
6
7
8
探究
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
∠1,∠2,···,∠8中,哪些是同位角?它们的度数具有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
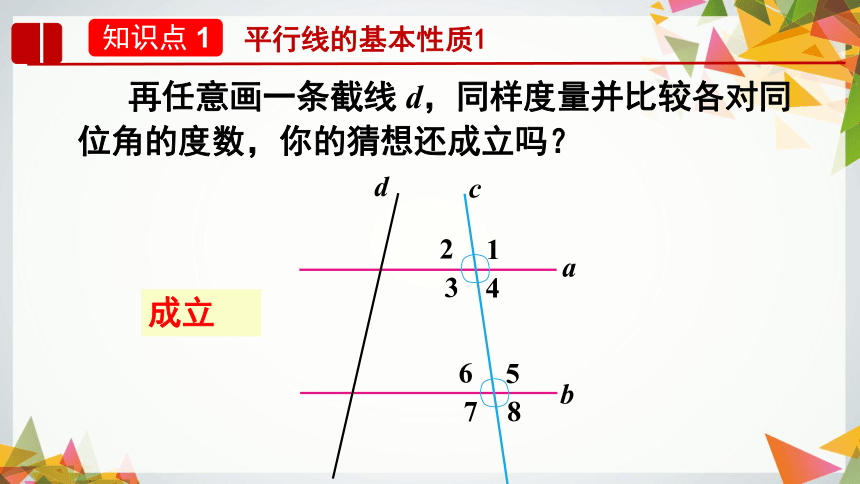
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
核心知识点一
平行线的基本性质1
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
思考
核心知识点二
平行线的基本性质2
如图,直线 a∥b ,c 是截线,那么?1 与?2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
核心知识点二
平行线的基本性质2
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
核心知识点三
平行线的基本性质3
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°。
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
例2 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A与∠D 互补,∠B与∠C 互补.
例3 如图,是一块梯形铁片的残余部分,量得∠A = 100?,∠B = 115?,梯形的另外两个角分别是多少度?
于是∠D = 180?-∠A
= 180?-100? = 80? ,
∠C = 180?-∠B
= 180?-115? = 65? .
所以,梯形的另外两个角分别是80?,65? .
例3 如图,是一块梯形铁片的残余部分,量得∠A = 100?,∠B = 115?,梯形的另外两个角分别是多少度?
答:∠2 = 110?.因为AB∥CD,∠1 和 ∠2 是内错角,根据两直线平行,内错角相等,得到∠1 = ∠2.因为∠1 = 110?,所以∠2 = 110?.
例4 如图,平行线 AB ,CD 被直线 AE 所截.
从∠1 = 110?.可以知道∠2是多少度吗?为什么?
图形
已知
结果
理由
a∥b
∠1=∠3
∠2=∠4
a∥b
两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
谢谢观看
人教版数学七年级下册
第五章 相交线与平行线
2. 能够根据平行线的性质进行简单的推理.(难点)
2
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;(重点)
1
判定方法1 同位角相等, 两直线平行.
判定方法2 内错角相等, 两直线平行.
判定方法3 同旁内角互补,两直线平行.
结 论
平行线的判定
新课导入
条件
两
直
线
平
行
条 件
结 论
?
两条平行线
被第三条直
线所截
同位角?
内错角?
同旁内角?
条 件
结 论
思考
两条平行线被第三条直线截得的同位角会具有怎样的数量关系?
核心知识点一
平行线的基本性质1
如图,已知直线 a∥b ,c是截线.
b
a
c
1
2
3
4
5
6
7
8
探究
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
∠1,∠2,···,∠8中,哪些是同位角?它们的度数具有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角具有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
归纳
核心知识点一
平行线的基本性质1
上一节,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行”. 类似地,你能由性质 1 推出两条平行线被第三条直线所截,内错角之间的关系吗?
思考
核心知识点二
平行线的基本性质2
如图,直线 a∥b ,c 是截线,那么?1 与?2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
归纳
核心知识点二
平行线的基本性质2
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
核心知识点三
平行线的基本性质3
例1 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
解:因为梯形上、下底互相平行,所以
∠A与∠D互补, ∠B与∠C互补.
所以梯形的另外两个角分别是80°、65°。
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
例2 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3,
∵两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A与∠D 互补,∠B与∠C 互补.
例3 如图,是一块梯形铁片的残余部分,量得∠A = 100?,∠B = 115?,梯形的另外两个角分别是多少度?
于是∠D = 180?-∠A
= 180?-100? = 80? ,
∠C = 180?-∠B
= 180?-115? = 65? .
所以,梯形的另外两个角分别是80?,65? .
例3 如图,是一块梯形铁片的残余部分,量得∠A = 100?,∠B = 115?,梯形的另外两个角分别是多少度?
答:∠2 = 110?.因为AB∥CD,∠1 和 ∠2 是内错角,根据两直线平行,内错角相等,得到∠1 = ∠2.因为∠1 = 110?,所以∠2 = 110?.
例4 如图,平行线 AB ,CD 被直线 AE 所截.
从∠1 = 110?.可以知道∠2是多少度吗?为什么?
图形
已知
结果
理由
a∥b
∠1=∠3
∠2=∠4
a∥b
两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
谢谢观看
