4.1.1 变量与函数 课件(共24张PPT)
文档属性
| 名称 | 4.1.1 变量与函数 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 18:24:55 | ||
图片预览








文档简介
(共24张PPT)
变量与函数
湘教版·八年级数学下册
上课课件
第4章
一次函数
学习目标
【知识与技能】
借助简单实例,学生初步感知用常量与变量来刻画一些简单的数学问题,能指出具体问题中的常量、变量.初步理解存在一类变量可以用函数方式来刻画,能举出涉及两个变量的实例,并指出由哪一个变量确定另一个变量,这两个变量是否具有函数关系.初步理解对应的思想,体会函数概念的核心是两个变量之间的特殊对应关系,能判断两个变量间是否具有函数关系.
【过程与方法】
借助简单实例,引领学生参与变量的发现和函数概念的形成过程,体会从生活实例抽象出数学知识的方法,感知现实世界中变量之间联系的复杂性,数学研究从最简单的情形入手,化繁为简.
【情感态度】
从学生熟悉、感兴趣的实例引入课题,引领学生参与变量的发现和函数概念的形成过程,体验“发现、创造”数学知识的乐趣.学生初步感知实际生活蕴藏着丰富的数学知识,感知数学是有用、有趣的学科.
【教学重点】
借助简单实例,从两个变量间的特殊对应关系抽象出函数的概念.
【教学难点】
怎样理解“唯一对应”.
情境导入
我们生活在一个运动的世界中,周围的事物都是运动的.
这些自然现象和日常生活中,我们经常会遇到许多变化的量,其中有些量随着另一些量的变化而变化.
探索新知
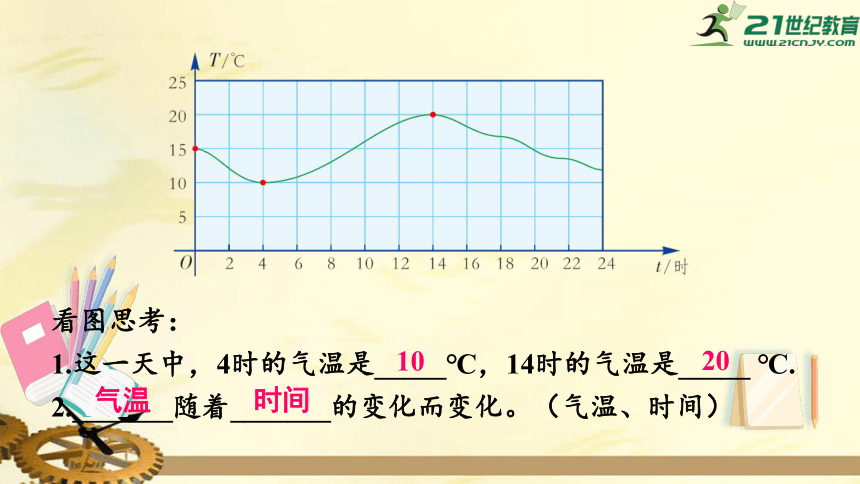
1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,它反映了该地某一天的气温T(℃)是如何随时间t的变化而变化的,你能从图中得到哪些信息?
看图思考:
1.这一天中,4时的气温是_____℃,14时的气温是_____
℃.
2._______随着_______的变化而变化。(气温、时间)
10
20
气温
时间
2.当正方形的边长x分别取1,2,3,4,5,…时,正方形的面积S分别是多少?试填写下表:
1
4
9
16
25
36
49
观察思考:
1.正方形的________随着________的变化而变化.
2.当边长x取定一个值时,面积S有______(唯一或不唯一)的值与它对应.
面积S
边长x
唯一
3.某城市居民用的天然气,1m3收费2.88元,使用x(m3)天然气应缴纳的费用y(元)为y=2.88x.当x=10时,缴纳的费用为多少?
观察思考:
1.______________________随着____________________的变化而变化.
2.当x=10时,y=_____
(元);当x=20时,y=_____(元)
3.当所用天然气的体积x取定一个值时,使用天然气缴纳的费用y有______(唯一或不唯一)的值与它对应.
使用天然气缴纳的费用y
随所用天然气的体积x
28.8
57.6
唯一
总结归纳
在某一变化过程中,取值会发生变化的量称为变量,取值固定不变的量称为常量(或常数).
注意:
1.判断一个量是不是变量关键是看在变化过程中,这个量是否可以取不同的数值;
2.
π是一个无理数,属于常量.
上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应缴纳的费用y等都是变量.
使用每一方米天然气应交纳2.88元,2.88是常量.
根据以上3个问题思考:
(1)以上每个变化过程中都有几个变量?
(2)变量间是怎样在变化的?
1.
每个变化的过程中都存在着两个变量;
2.当其中的一个变量变化时,另一个变量也在随着变化;
3.当一个变量确定一个值时,另一个变量有唯一的一个值与它对应.
总结归纳
一般地,变量y随着变量x的变化而变化,并且对于x的每一个值,
y都有唯一的一个值与它对应,我们就说y是x的函数,记作y=f(x).此时称x是自变量,
y是因变量,对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作y=f(a).
1.在问题1中,_________是自变量,_________是________的函数.
2.在问题2中,正方形的边长是_________,正方形的面积是边长的_________.
3.在问题3中,___________________是自变量,___________是__________________的函数.
时间t
气温T
时间t
自变量
函数
所用天然气的体积x
应缴纳费用y
所用天然气的体积x
在考虑两个变量间的函数时,还要注意自变量的取值范围.
如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.
如图,已知圆柱的高是4cm,底面半径是r(cm),当圆柱的底面半径r由小变大时,圆柱的体积V(cm3)是r的函数.
(1)用含r的代数式来表示圆柱的体积V,指出自变量r的取值范围.
(2)当r=5
,10时,V是多少(结果保留π)?
【教材P111页】
解:(1)圆柱的体积V=4πr2,自变量r的取值范围是r>0.
(2)当r=5时,V=4π×25=100π(cm3);
当r=10时,V=4π×100=400π(cm3).
练习
1.
指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h
的速度匀速行驶,行驶的路程s(km)
与行驶时间t(h).
(2)圆的半径r和圆面积S满足:S=πr2
.
(3)银行的存款利率P与存期t.
行驶的路程s随行驶时间t的变化而变化.
圆的面积S随半径r的变化而变化.
存款利率P随存期t的变化而变化.
2.
如图,A港口某天受潮汐的影响,24小时内港口水深h(m)
随时间t(时)的变化而变化.
(1)水深h是时间t的函数吗?
不是.
2.
如图,A港口某天受潮汐的影响,24小时内港口水深h(m)
随时间t(时)的变化而变化.
(2)当t分别取4,10,17时,h是多少?
当t=4,h=5m;t=10,h=7m;t=17,h=5m.
随堂练习
1.汽车以70千米/时的速度匀速行驶,行驶路程为s千米,行驶时间为t小时,从而s=70t,则下列判断中错误的是(
)
A.s是常量
B.s是变量
C.70是常量
D.t是变量
2.一个正方形的边长为3
cm,它的各边边长减少x
cm后,得到的新正方形的周长为y
cm,y与x间的函数关系式是(
)
A.y=12-4x
B.y=4x-12
C.y=12-x
D.以上都不对
A
A
3.函数
中自变量x的取值范围是__________.
4.一块形状为等腰三角形的铁皮,周长为10,底边长为y,腰长为x.
(1)求y与x之间的关系式;
(2)求自变量x的取值范围.
x≥3
y=10-2x
∵10-2x>0,2x>10-2x,∴2.5课堂小结
1.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一的一个值与它对应,那么我们就说x是自变量,y是x的函数.
2.判断两个变量是否有函数关系,要同时满足两个条件:
(1)有两个变量
(2)当其中的一个变量变化时,另一个变量也在随着变化;
(3)自变量x每取一个确定的值,函数y都有唯一的值与之对应.
课堂小结
3.这种唯一对应性是指y是唯一的.
x可以有多个值,但是对应的y值只能有一个.
4.函数的本质就是变量间的对应关系.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
变量与函数
湘教版·八年级数学下册
上课课件
第4章
一次函数
学习目标
【知识与技能】
借助简单实例,学生初步感知用常量与变量来刻画一些简单的数学问题,能指出具体问题中的常量、变量.初步理解存在一类变量可以用函数方式来刻画,能举出涉及两个变量的实例,并指出由哪一个变量确定另一个变量,这两个变量是否具有函数关系.初步理解对应的思想,体会函数概念的核心是两个变量之间的特殊对应关系,能判断两个变量间是否具有函数关系.
【过程与方法】
借助简单实例,引领学生参与变量的发现和函数概念的形成过程,体会从生活实例抽象出数学知识的方法,感知现实世界中变量之间联系的复杂性,数学研究从最简单的情形入手,化繁为简.
【情感态度】
从学生熟悉、感兴趣的实例引入课题,引领学生参与变量的发现和函数概念的形成过程,体验“发现、创造”数学知识的乐趣.学生初步感知实际生活蕴藏着丰富的数学知识,感知数学是有用、有趣的学科.
【教学重点】
借助简单实例,从两个变量间的特殊对应关系抽象出函数的概念.
【教学难点】
怎样理解“唯一对应”.
情境导入
我们生活在一个运动的世界中,周围的事物都是运动的.
这些自然现象和日常生活中,我们经常会遇到许多变化的量,其中有些量随着另一些量的变化而变化.
探索新知
1.下图是某地气象站用自动温度记录仪描出的某一天的温度曲线,它反映了该地某一天的气温T(℃)是如何随时间t的变化而变化的,你能从图中得到哪些信息?
看图思考:
1.这一天中,4时的气温是_____℃,14时的气温是_____
℃.
2._______随着_______的变化而变化。(气温、时间)
10
20
气温
时间
2.当正方形的边长x分别取1,2,3,4,5,…时,正方形的面积S分别是多少?试填写下表:
1
4
9
16
25
36
49
观察思考:
1.正方形的________随着________的变化而变化.
2.当边长x取定一个值时,面积S有______(唯一或不唯一)的值与它对应.
面积S
边长x
唯一
3.某城市居民用的天然气,1m3收费2.88元,使用x(m3)天然气应缴纳的费用y(元)为y=2.88x.当x=10时,缴纳的费用为多少?
观察思考:
1.______________________随着____________________的变化而变化.
2.当x=10时,y=_____
(元);当x=20时,y=_____(元)
3.当所用天然气的体积x取定一个值时,使用天然气缴纳的费用y有______(唯一或不唯一)的值与它对应.
使用天然气缴纳的费用y
随所用天然气的体积x
28.8
57.6
唯一
总结归纳
在某一变化过程中,取值会发生变化的量称为变量,取值固定不变的量称为常量(或常数).
注意:
1.判断一个量是不是变量关键是看在变化过程中,这个量是否可以取不同的数值;
2.
π是一个无理数,属于常量.
上述问题中,时间t,气温T;正方形的边长x,面积S;使用天然气的体积x,应缴纳的费用y等都是变量.
使用每一方米天然气应交纳2.88元,2.88是常量.
根据以上3个问题思考:
(1)以上每个变化过程中都有几个变量?
(2)变量间是怎样在变化的?
1.
每个变化的过程中都存在着两个变量;
2.当其中的一个变量变化时,另一个变量也在随着变化;
3.当一个变量确定一个值时,另一个变量有唯一的一个值与它对应.
总结归纳
一般地,变量y随着变量x的变化而变化,并且对于x的每一个值,
y都有唯一的一个值与它对应,我们就说y是x的函数,记作y=f(x).此时称x是自变量,
y是因变量,对于自变量x取的每一个值a,因变量y的对应值称为函数值,记作y=f(a).
1.在问题1中,_________是自变量,_________是________的函数.
2.在问题2中,正方形的边长是_________,正方形的面积是边长的_________.
3.在问题3中,___________________是自变量,___________是__________________的函数.
时间t
气温T
时间t
自变量
函数
所用天然气的体积x
应缴纳费用y
所用天然气的体积x
在考虑两个变量间的函数时,还要注意自变量的取值范围.
如上述第1个问题中,自变量t的取值范围是0≤t≤24;而第2、3个问题中,自变量x的取值范围分别是x>0,x≥0.
如图,已知圆柱的高是4cm,底面半径是r(cm),当圆柱的底面半径r由小变大时,圆柱的体积V(cm3)是r的函数.
(1)用含r的代数式来表示圆柱的体积V,指出自变量r的取值范围.
(2)当r=5
,10时,V是多少(结果保留π)?
【教材P111页】
解:(1)圆柱的体积V=4πr2,自变量r的取值范围是r>0.
(2)当r=5时,V=4π×25=100π(cm3);
当r=10时,V=4π×100=400π(cm3).
练习
1.
指出下列变化过程中,哪个变量随着另一个变量的变化而变化?
(1)一辆汽车以80km/h
的速度匀速行驶,行驶的路程s(km)
与行驶时间t(h).
(2)圆的半径r和圆面积S满足:S=πr2
.
(3)银行的存款利率P与存期t.
行驶的路程s随行驶时间t的变化而变化.
圆的面积S随半径r的变化而变化.
存款利率P随存期t的变化而变化.
2.
如图,A港口某天受潮汐的影响,24小时内港口水深h(m)
随时间t(时)的变化而变化.
(1)水深h是时间t的函数吗?
不是.
2.
如图,A港口某天受潮汐的影响,24小时内港口水深h(m)
随时间t(时)的变化而变化.
(2)当t分别取4,10,17时,h是多少?
当t=4,h=5m;t=10,h=7m;t=17,h=5m.
随堂练习
1.汽车以70千米/时的速度匀速行驶,行驶路程为s千米,行驶时间为t小时,从而s=70t,则下列判断中错误的是(
)
A.s是常量
B.s是变量
C.70是常量
D.t是变量
2.一个正方形的边长为3
cm,它的各边边长减少x
cm后,得到的新正方形的周长为y
cm,y与x间的函数关系式是(
)
A.y=12-4x
B.y=4x-12
C.y=12-x
D.以上都不对
A
A
3.函数
中自变量x的取值范围是__________.
4.一块形状为等腰三角形的铁皮,周长为10,底边长为y,腰长为x.
(1)求y与x之间的关系式;
(2)求自变量x的取值范围.
x≥3
y=10-2x
∵10-2x>0,2x>10-2x,∴2.5
1.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一的一个值与它对应,那么我们就说x是自变量,y是x的函数.
2.判断两个变量是否有函数关系,要同时满足两个条件:
(1)有两个变量
(2)当其中的一个变量变化时,另一个变量也在随着变化;
(3)自变量x每取一个确定的值,函数y都有唯一的值与之对应.
课堂小结
3.这种唯一对应性是指y是唯一的.
x可以有多个值,但是对应的y值只能有一个.
4.函数的本质就是变量间的对应关系.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
