4.3 一次函数的图像(第2课时) 一次函数的图象和性质 课件(共29张PPT)
文档属性
| 名称 | 4.3 一次函数的图像(第2课时) 一次函数的图象和性质 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
一次函数的图象和性质
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
理解直线y=kx+b与y=kx之间的位置关系,使学生理解掌握并会做出一次函数的图象.
【过程与方法】
通过一次函数的图象学习,体验数形结合法的应用,培养推理及抽象思维能力.
【情感态度】
通过画函数图象并借助图象研究函数的性质,体验数与形的内在联系,感受函数图象的简洁美.
【教学重点】
作一次函数的图象
【教学难点】
对一次函数y=kx+b(k、b为常数)中k、b的数与形的联系的理解.
复习回顾
1.函数图象概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
2.一次函数的解析式:
y=kx+b(k≠0)
3.正比例函数的解析式:
y=kx(k≠0)
4.作函数图象有几个步骤?
列表
描点
连线
5.正比例函数图象有什么特点?
正比例函数y=kx(k为常数,k≠0)的图象是经过点(0,0)和点(1,k)的一条直线,直线上的点与y=kx对应的x、y的值一一对应.
当k>0时,图象过一、三象限,y随x的增大而增大;
当k<0时,图象过二、四象限,y随x的增大而减小.
探索新知
思考
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?它们图象之间有什么关系?
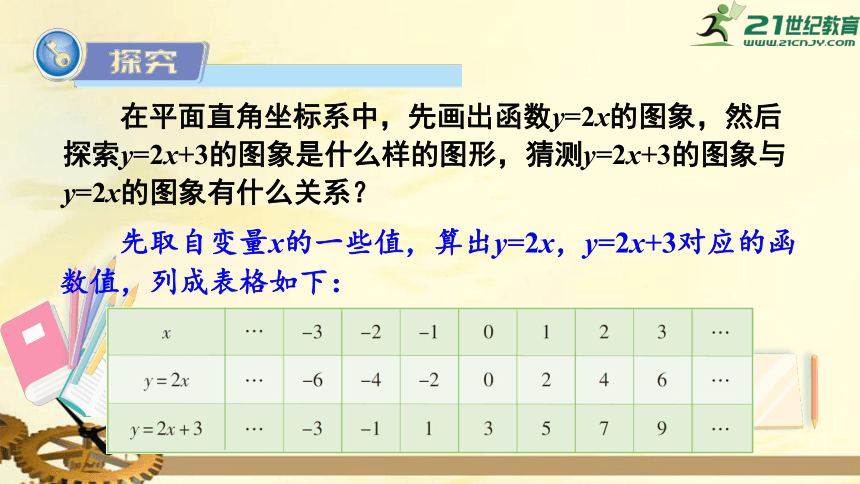
在平面直角坐标系中,先画出函数y=2x的图象,然后探索y=2x+3的图象是什么样的图形,猜测y=2x+3的图象与y=2x的图象有什么关系?
先取自变量x的一些值,算出y=2x,y=2x+3对应的函数值,列成表格如下:
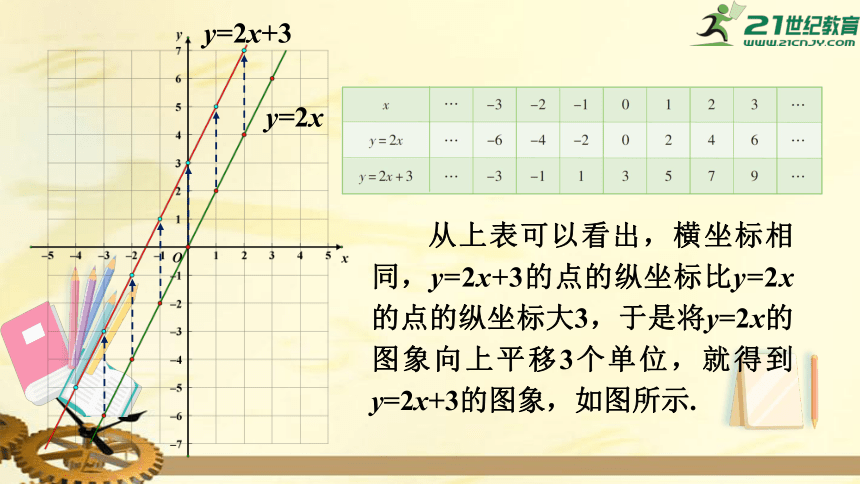
从上表可以看出,横坐标相同,y=2x+3的点的纵坐标比y=2x的点的纵坐标大3,于是将y=2x的图象向上平移3个单位,就得到y=2x+3的图象,如图所示.
y=2x
y=2x+3
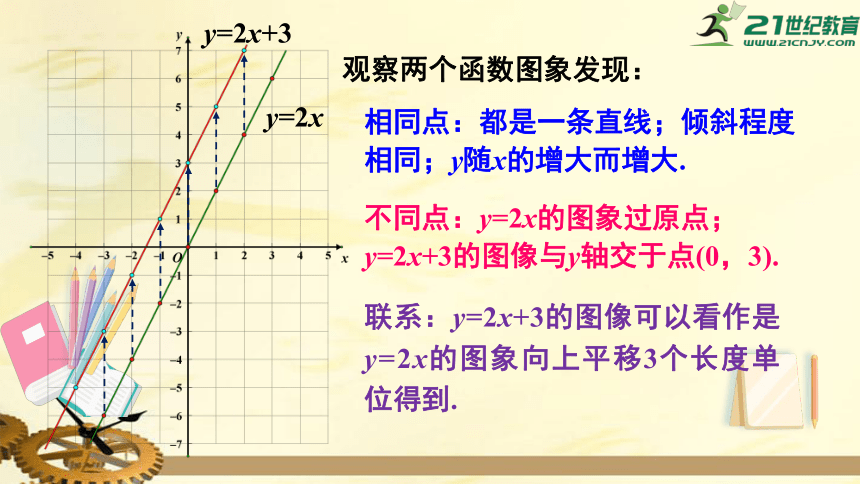
观察两个函数图象发现:
相同点:都是一条直线;倾斜程度相同;y随x的增大而增大.
不同点:y=2x的图象过原点;y=2x+3的图像与y轴交于点(0,3).
联系:y=2x+3的图像可以看作是y=2x的图象向上平移3个长度单位得到.
y=2x
y=2x+3
y=2x
y=2x+3
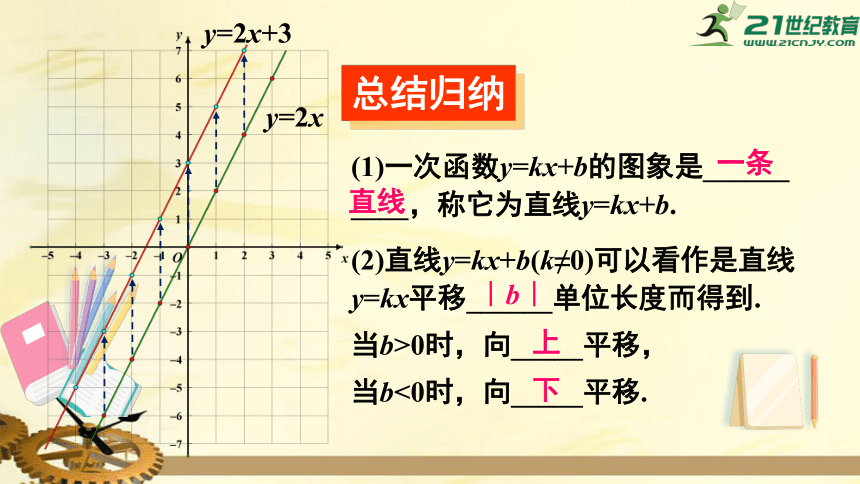
总结归纳
(1)一次函数y=kx+b的图象是______
____,称它为直线y=kx+b.
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平移______单位长度而得到.
当b>0时,向_____平移,
当b<0时,向_____平移.
一条
直线
|b|
上
下
一次函数y=kx+b表达式的平移公式
y=kx+b
y=kx+(b+m)
向上平移m个单位
向下平移m个单位
y=kx+(b-m)
y=k(x-m)+b
y=k(x+m)+b
向左平移m个单位
向右平移m个单位
上下平移:常数项b增加或减少;
左右平移:自变量x增加或减少.
一次函数y=kx+b(k≠0)的图象是一条直线,因为两点确定一条直线,所以画一次函数的图象时,只要描出两点即可画出一条直线.
选哪两个点最简单?
一般选直线与坐标轴的两个交点.
画出一次函数y=-2x-3的图象.
解:当x=0时,y=-3;
当x=1时,y=-5.
在平面直角坐标系中描出两点A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数y=-2x-3的图象,如图所示.
A(0,-3)
B(1,-5)
y=-2x-3
y=-2x-3
y=2x+3
观察画出的一次函数y=2x+3,y=-2x-3的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗?
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
y=-2x-3
y=2x+3
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
对于y=-2x-3,当自变量x的取值由小变大时,对应的函数值y由大变小.
一般地,一次函数y=kx+b(k,b为常数,k≠0)具有如下性质:
图中描述了某一天小亮从家骑车去书店购书,然后又骑车回家的情况。你能说出小亮在路上的情形吗?
分析:小亮骑车离家的距离y是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.
解:第一段是从原点出发的线段OA.
从横坐标看出,小亮路上花了30min,当横坐标从0变化到30时,纵坐标均匀增加,这说明小亮从家出发匀速前进30min,到达书店.
第二段是与x轴平行的一条线段AB,当横坐标从30变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min.
第三段是与x轴有交点的线段BC.从横坐标看出,小亮路上花了40min.当横坐标从60变化到100时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
练习
1.(1)将直线y=3x向下平移2个单位,得到直线____________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________.
y=3x-2
y=-x
2.过两点分别作出一次函数
和
的图象,并指出函数值如何随自变量的变化而变化?
当自变量x的取值由小变大时,对应的函数值y由小变大.
当自变量x的取值由小变大时,对应的函数值y由大变小.
随堂练习
1.下列函数中,y随x的增大而减小的函数是(
)
A.
y=2x+8
B.
y=-2+4x
C.
y=-2x+8
D.
y=4x
2.已知一次函数y=kx+b的图象如图所示,则k、b的符号是(
)
A.
k>0,b>0
B.
k>0,b<0
C.
k<0,b>0
D.
k<0,b<0
C
B
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k=_____,b=_____.
y=-2x
-2
-3
4.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程s(千米)和行驶时间t(小时)之间的关系,根据所给图象,解答下列问题:
(1)写出甲的行驶路程和行驶时间t(t≥0)之间的函数关系式;
s=2t
(2)在哪一段时间内,甲的行驶速度小于乙的行驶速度;在哪一段时间里,甲的速度大于乙的速度?
解:在01时,甲的速度大于乙的行驶速度;
(3)从图象中你还能获得什么信息?请写出其中的一条.
课堂小结
通过本课时的学习,需要我们掌握
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
一次函数
y=kx+b(k≠0)
(特别地,当b=0时,为正比例函数y=kx)
k、b符号
k>0
k<0
b>0
b<0
b=0
b>0
b<0
b=0
图象
经过象限
一、二、三
一、三、四
一、三
一、二、四
二、三、四
二、四
增减性
y随x的增大而增大
y随x的增大而减小
一次函数的图象和性质
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
一次函数的图象和性质
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
理解直线y=kx+b与y=kx之间的位置关系,使学生理解掌握并会做出一次函数的图象.
【过程与方法】
通过一次函数的图象学习,体验数形结合法的应用,培养推理及抽象思维能力.
【情感态度】
通过画函数图象并借助图象研究函数的性质,体验数与形的内在联系,感受函数图象的简洁美.
【教学重点】
作一次函数的图象
【教学难点】
对一次函数y=kx+b(k、b为常数)中k、b的数与形的联系的理解.
复习回顾
1.函数图象概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的横坐标和纵坐标,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的图象.
2.一次函数的解析式:
y=kx+b(k≠0)
3.正比例函数的解析式:
y=kx(k≠0)
4.作函数图象有几个步骤?
列表
描点
连线
5.正比例函数图象有什么特点?
正比例函数y=kx(k为常数,k≠0)的图象是经过点(0,0)和点(1,k)的一条直线,直线上的点与y=kx对应的x、y的值一一对应.
当k>0时,图象过一、三象限,y随x的增大而增大;
当k<0时,图象过二、四象限,y随x的增大而减小.
探索新知
思考
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线吗?它们图象之间有什么关系?
在平面直角坐标系中,先画出函数y=2x的图象,然后探索y=2x+3的图象是什么样的图形,猜测y=2x+3的图象与y=2x的图象有什么关系?
先取自变量x的一些值,算出y=2x,y=2x+3对应的函数值,列成表格如下:
从上表可以看出,横坐标相同,y=2x+3的点的纵坐标比y=2x的点的纵坐标大3,于是将y=2x的图象向上平移3个单位,就得到y=2x+3的图象,如图所示.
y=2x
y=2x+3
观察两个函数图象发现:
相同点:都是一条直线;倾斜程度相同;y随x的增大而增大.
不同点:y=2x的图象过原点;y=2x+3的图像与y轴交于点(0,3).
联系:y=2x+3的图像可以看作是y=2x的图象向上平移3个长度单位得到.
y=2x
y=2x+3
y=2x
y=2x+3
总结归纳
(1)一次函数y=kx+b的图象是______
____,称它为直线y=kx+b.
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平移______单位长度而得到.
当b>0时,向_____平移,
当b<0时,向_____平移.
一条
直线
|b|
上
下
一次函数y=kx+b表达式的平移公式
y=kx+b
y=kx+(b+m)
向上平移m个单位
向下平移m个单位
y=kx+(b-m)
y=k(x-m)+b
y=k(x+m)+b
向左平移m个单位
向右平移m个单位
上下平移:常数项b增加或减少;
左右平移:自变量x增加或减少.
一次函数y=kx+b(k≠0)的图象是一条直线,因为两点确定一条直线,所以画一次函数的图象时,只要描出两点即可画出一条直线.
选哪两个点最简单?
一般选直线与坐标轴的两个交点.
画出一次函数y=-2x-3的图象.
解:当x=0时,y=-3;
当x=1时,y=-5.
在平面直角坐标系中描出两点A(0,-3),B(1,-5),过这两点作直线,则这条直线是一次函数y=-2x-3的图象,如图所示.
A(0,-3)
B(1,-5)
y=-2x-3
y=-2x-3
y=2x+3
观察画出的一次函数y=2x+3,y=-2x-3的图象,你能发现当自变量x的取值由小变大时,对应的函数值如何变化吗?
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
y=-2x-3
y=2x+3
对于y=2x+3,当自变量x的取值由小变大时,对应的函数值y由小变大.
对于y=-2x-3,当自变量x的取值由小变大时,对应的函数值y由大变小.
一般地,一次函数y=kx+b(k,b为常数,k≠0)具有如下性质:
图中描述了某一天小亮从家骑车去书店购书,然后又骑车回家的情况。你能说出小亮在路上的情形吗?
分析:小亮骑车离家的距离y是时间x的函数,这个函数图象由3条线段组成,每一条线段代表一个阶段的活动.
解:第一段是从原点出发的线段OA.
从横坐标看出,小亮路上花了30min,当横坐标从0变化到30时,纵坐标均匀增加,这说明小亮从家出发匀速前进30min,到达书店.
第二段是与x轴平行的一条线段AB,当横坐标从30变化到60时,纵坐标没有变化,这说明小亮在书店购书待了30min.
第三段是与x轴有交点的线段BC.从横坐标看出,小亮路上花了40min.当横坐标从60变化到100时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
练习
1.(1)将直线y=3x向下平移2个单位,得到直线____________;
(2)将直线y=-x-5向上平移5个单位,得到直线_____________.
y=3x-2
y=-x
2.过两点分别作出一次函数
和
的图象,并指出函数值如何随自变量的变化而变化?
当自变量x的取值由小变大时,对应的函数值y由小变大.
当自变量x的取值由小变大时,对应的函数值y由大变小.
随堂练习
1.下列函数中,y随x的增大而减小的函数是(
)
A.
y=2x+8
B.
y=-2+4x
C.
y=-2x+8
D.
y=4x
2.已知一次函数y=kx+b的图象如图所示,则k、b的符号是(
)
A.
k>0,b>0
B.
k>0,b<0
C.
k<0,b>0
D.
k<0,b<0
C
B
3.函数y=kx+b的图象平行于直线y=-2x,且与y轴交于点(0,3),则k=_____,b=_____.
y=-2x
-2
-3
4.如图,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程s(千米)和行驶时间t(小时)之间的关系,根据所给图象,解答下列问题:
(1)写出甲的行驶路程和行驶时间t(t≥0)之间的函数关系式;
s=2t
(2)在哪一段时间内,甲的行驶速度小于乙的行驶速度;在哪一段时间里,甲的速度大于乙的速度?
解:在0
(3)从图象中你还能获得什么信息?请写出其中的一条.
课堂小结
通过本课时的学习,需要我们掌握
1.一次函数的一般形式及一次函数与正比例函数的关系.
2.一次函数的图象与性质.
一次函数
y=kx+b(k≠0)
(特别地,当b=0时,为正比例函数y=kx)
k、b符号
k>0
k<0
b>0
b<0
b=0
b>0
b<0
b=0
图象
经过象限
一、二、三
一、三、四
一、三
一、二、四
二、三、四
二、四
增减性
y随x的增大而增大
y随x的增大而减小
一次函数的图象和性质
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
