4.4 用待定系数法确定一次函数表达式 课件(共27张PPT)
文档属性
| 名称 | 4.4 用待定系数法确定一次函数表达式 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
4.4
用待定系数法确定一次函数表达式
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生了解两个条件确定一个一次函数;一个条件确定一个正比例函数.
2.能由两个条件确定解析式或者能根据函数的图象确定一次函数的解析式.
【过程与方法】
1.通过类比的方法学习一次函数,体会数学研究方法多样性.
2.进一步提高分析概括、总结归纳能力.
3.利用数形结合思想,进一步分析一次函数与正比例函数的联系,从而提高比较鉴别能力.
【情感态度】
1.积极思考、勇跃发言,养成良好的学习习惯.
2.独立思考、合作探究,培养学生的思维方法.
【教学重点】
会用待定系数法确定一次函数的表达式.
【教学难点】
从图象上捕捉信息.
复习回顾
画出函数y=2x,y=
+3的图象.
y=2x
许多实际问题的解决都需要求出一次函数的表达式.
怎样才能简便地求出一次函数的表达式呢?
探索新知
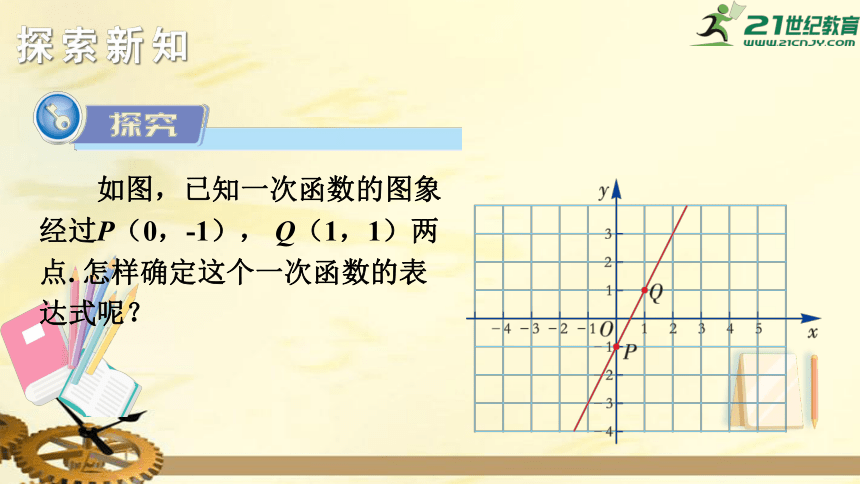
如图,已知一次函数的图象经过P(0,-1),
Q(1,1)两点.
怎样确定这个一次函数的表达式呢?
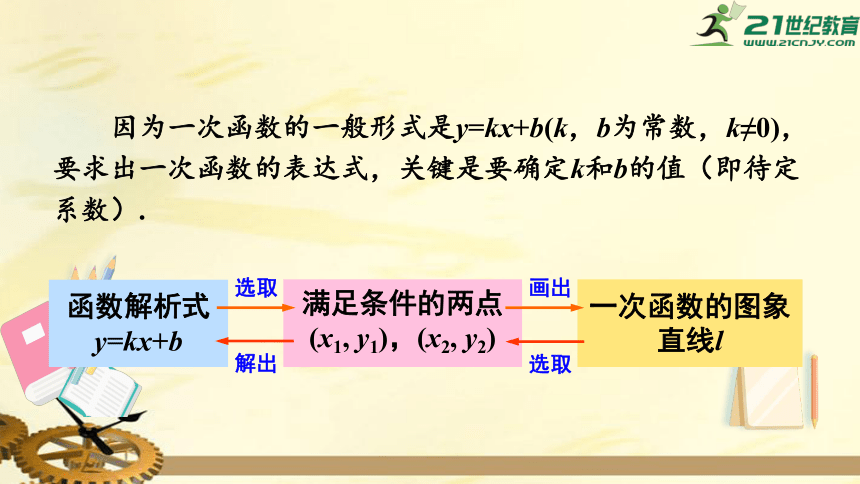
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,
y1),(x2,
y2)
一次函数的图象
直线l
选取
画出
选取
解出
因为P(0,-1)和Q(1,1)都在该函数图象上,
因此它们的坐标应满足y=kx+b,将这两点坐标代入该式中,得到一个关于k,b的二元一次方程组:
k·0
+
b
=-1,
k
+
b
=
1.
解这个方程组,得
k
=
2,
b
=-1.
所以,这个一次函数的表达式为y=2x-1.
像这样,通过先设定函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数的表达式的方法称为待定系数法.
你能归纳出待定系数法求函数表达式的基本步骤吗?
总结归纳
(1)设这个函数表达式为y=kx+b;
(2)把已知点的坐标x,y的对应值代入解析式列出方程组;
(3)解这个二元一次方程组,求出k、b的值;
(4)把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
温度的度量有两种:摄氏温度和华氏温度.在1个标准大气压下,水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32℉.已知摄氏温度与华氏温度满足一次函数关系,你能不能想出一个办法将华氏温度换算成摄氏温度?
【教材P130页】
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C=kF+b
由已知条件,得
212k
+
b
=100,
32k
+
b
=
0.
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
【教材P130页】
(1)求y关于x的函数表达式;
解:设一次函数的表达式为y=kx+b,
由于点P(2,
30),Q(6,
10)都在一次函数图像上,将这两点坐标带入表达式,得
2k
+
b
=
30,
6k
+
b
=
10.
解得k=-5,b=40.
所以y=-5x+40.
(2)一箱油可供拖拉机工作几小时?
解:当剩余油量为0时,即y=0时,
得-5x+40=0,x=8.
所以一箱油可供拖拉机工作8h.
练习
1.把84℉换算成摄氏温度.
解:由摄氏温度与华氏温度的函数关系得
解得C≈28.9(℃)
因此,把温度84℉换算成摄氏温度约为28.9℃.
【教材P131页】
2.已知一次函数的图象经过两点A(-1,
3),B(2,
-5),求这个函数的表达式.
解:设一次函数的表达式为y=kx+b,
由于点A(-1,
3),B(2,
-5)都在一次函数图像上,将这两点坐标带入表达式,得
-k
+
b
=
3,
2k
+
b
=
-5.
解得
因此所求一次函数的解析式为
【教材P131页】
3.酒精的体积随温度的升高而增大,体积与温度之间在一定范围内近似于一次函数关系,现测得一定量的酒精在0℃时的体积为5.250L,在40℃时的体积为5.481L,求这些酒精在10℃和30℃时的体积各是多少?
解:设体积与温度之间的函数关系为y=kx+b,由已知得
k·0
+
b
=
5.250,
k·40
+
b
=
5.481.
解得
k=0.005775,b=
5.250
.
因此所求一次函数的解析式为
y=0.005775x+5.250.
【教材P131页】
在10
℃,即x=10时,
体积y=0.005775×10
+5.250=5.30775(L).
在30
℃,即x=30时,
体积y=0.005775×30
+5.250=5.42325(L).
答:这些酒精在10
℃和30
℃时的体积各是5.30775L
和5.42325L.
随堂练习
1.
如图,直线AB对应的函数表达式为(
)
A.
B.
C.
D.
A
2.已知一次函数y=kx+b,当x=1时,y=3,当x=0时,y=1,则当x=2时,y的值是(
)
A.2
B.3
C.4
D.5
D
3.一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x,那么当1≤x≤2时,y关于x的函数解析式为_______________.
y=100x-40
4.某客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要购买行李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图所示.
求:(1)y与x之间的函数关系式;
(2)问旅客最多可免费携带行李多少千克?
(1)解:设一次函数的表达式为y=kx+b,
由于点(60,
6),B(80,
10)都在一次函数图像上,将这两点坐标带入表达式,得
60k
+
b
=
6,
80k
+
b
=
10.
解得
因此所求一次函数的解析式为
(2)令y=0,则x=30,即旅客最多可免费携带行李30千克.
课堂小结
1.求一次函数表达式的步骤:
(1)设一次函数一般式
(2)根据已知条件列出关于k,b的方程
(3)解方程,求k,b
(4)把k,b代回表达式中,写出表达式
--------设
--------列
--------解
--------写
2.求出表达式后已知其中一个量求另一个量
3.根据函数图象回答或求出相关问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
4.4
用待定系数法确定一次函数表达式
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生了解两个条件确定一个一次函数;一个条件确定一个正比例函数.
2.能由两个条件确定解析式或者能根据函数的图象确定一次函数的解析式.
【过程与方法】
1.通过类比的方法学习一次函数,体会数学研究方法多样性.
2.进一步提高分析概括、总结归纳能力.
3.利用数形结合思想,进一步分析一次函数与正比例函数的联系,从而提高比较鉴别能力.
【情感态度】
1.积极思考、勇跃发言,养成良好的学习习惯.
2.独立思考、合作探究,培养学生的思维方法.
【教学重点】
会用待定系数法确定一次函数的表达式.
【教学难点】
从图象上捕捉信息.
复习回顾
画出函数y=2x,y=
+3的图象.
y=2x
许多实际问题的解决都需要求出一次函数的表达式.
怎样才能简便地求出一次函数的表达式呢?
探索新知
如图,已知一次函数的图象经过P(0,-1),
Q(1,1)两点.
怎样确定这个一次函数的表达式呢?
因为一次函数的一般形式是y=kx+b(k,b为常数,k≠0),要求出一次函数的表达式,关键是要确定k和b的值(即待定系数).
函数解析式
y=kx+b
满足条件的两点
(x1,
y1),(x2,
y2)
一次函数的图象
直线l
选取
画出
选取
解出
因为P(0,-1)和Q(1,1)都在该函数图象上,
因此它们的坐标应满足y=kx+b,将这两点坐标代入该式中,得到一个关于k,b的二元一次方程组:
k·0
+
b
=-1,
k
+
b
=
1.
解这个方程组,得
k
=
2,
b
=-1.
所以,这个一次函数的表达式为y=2x-1.
像这样,通过先设定函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数的表达式的方法称为待定系数法.
你能归纳出待定系数法求函数表达式的基本步骤吗?
总结归纳
(1)设这个函数表达式为y=kx+b;
(2)把已知点的坐标x,y的对应值代入解析式列出方程组;
(3)解这个二元一次方程组,求出k、b的值;
(4)把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
温度的度量有两种:摄氏温度和华氏温度.在1个标准大气压下,水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32℉.已知摄氏温度与华氏温度满足一次函数关系,你能不能想出一个办法将华氏温度换算成摄氏温度?
【教材P130页】
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C=kF+b
由已知条件,得
212k
+
b
=100,
32k
+
b
=
0.
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数表达式;
(2)一箱油可供拖拉机工作几小时?
【教材P130页】
(1)求y关于x的函数表达式;
解:设一次函数的表达式为y=kx+b,
由于点P(2,
30),Q(6,
10)都在一次函数图像上,将这两点坐标带入表达式,得
2k
+
b
=
30,
6k
+
b
=
10.
解得k=-5,b=40.
所以y=-5x+40.
(2)一箱油可供拖拉机工作几小时?
解:当剩余油量为0时,即y=0时,
得-5x+40=0,x=8.
所以一箱油可供拖拉机工作8h.
练习
1.把84℉换算成摄氏温度.
解:由摄氏温度与华氏温度的函数关系得
解得C≈28.9(℃)
因此,把温度84℉换算成摄氏温度约为28.9℃.
【教材P131页】
2.已知一次函数的图象经过两点A(-1,
3),B(2,
-5),求这个函数的表达式.
解:设一次函数的表达式为y=kx+b,
由于点A(-1,
3),B(2,
-5)都在一次函数图像上,将这两点坐标带入表达式,得
-k
+
b
=
3,
2k
+
b
=
-5.
解得
因此所求一次函数的解析式为
【教材P131页】
3.酒精的体积随温度的升高而增大,体积与温度之间在一定范围内近似于一次函数关系,现测得一定量的酒精在0℃时的体积为5.250L,在40℃时的体积为5.481L,求这些酒精在10℃和30℃时的体积各是多少?
解:设体积与温度之间的函数关系为y=kx+b,由已知得
k·0
+
b
=
5.250,
k·40
+
b
=
5.481.
解得
k=0.005775,b=
5.250
.
因此所求一次函数的解析式为
y=0.005775x+5.250.
【教材P131页】
在10
℃,即x=10时,
体积y=0.005775×10
+5.250=5.30775(L).
在30
℃,即x=30时,
体积y=0.005775×30
+5.250=5.42325(L).
答:这些酒精在10
℃和30
℃时的体积各是5.30775L
和5.42325L.
随堂练习
1.
如图,直线AB对应的函数表达式为(
)
A.
B.
C.
D.
A
2.已知一次函数y=kx+b,当x=1时,y=3,当x=0时,y=1,则当x=2时,y的值是(
)
A.2
B.3
C.4
D.5
D
3.一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图所示,当0≤x≤1时,y关于x的函数解析式为y=60x,那么当1≤x≤2时,y关于x的函数解析式为_______________.
y=100x-40
4.某客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要购买行李票,行李票费用y(元)是行李重量x(千克)的一次函数,其图象如图所示.
求:(1)y与x之间的函数关系式;
(2)问旅客最多可免费携带行李多少千克?
(1)解:设一次函数的表达式为y=kx+b,
由于点(60,
6),B(80,
10)都在一次函数图像上,将这两点坐标带入表达式,得
60k
+
b
=
6,
80k
+
b
=
10.
解得
因此所求一次函数的解析式为
(2)令y=0,则x=30,即旅客最多可免费携带行李30千克.
课堂小结
1.求一次函数表达式的步骤:
(1)设一次函数一般式
(2)根据已知条件列出关于k,b的方程
(3)解方程,求k,b
(4)把k,b代回表达式中,写出表达式
--------设
--------列
--------解
--------写
2.求出表达式后已知其中一个量求另一个量
3.根据函数图象回答或求出相关问题
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
