4.5 一次函数的应用(第1课时) 利用一次函数解决实际问题 课件(共25张PPT)
文档属性
| 名称 | 4.5 一次函数的应用(第1课时) 利用一次函数解决实际问题 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
利用一次函数解决实际问题
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
复习回顾
1.一次函数的表达式为:
y=kx+b(k≠0)
2.待定系数法求一次函数表达式的步骤:
(1)设出一次函数表达式:
y=kx+b(k≠0)
(2)利用给定两点建立二元一次方程组:
(3)解二元一次方程组,得k和b的值,代入表达式即可.
某地为保护环境,鼓励节约用电,实行阶梯电价制度.
规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
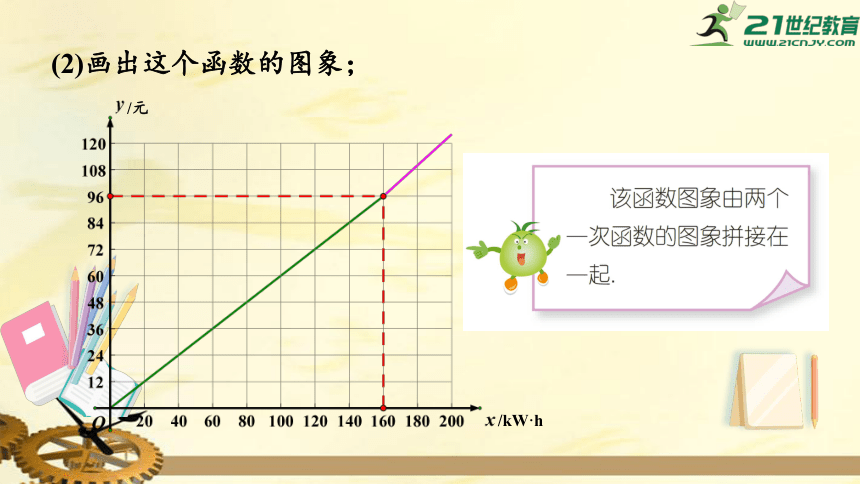
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
探索新知
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
解:电费与用电量相关.
当0≤x≤160时,y=0.6x;
当x>160时,
y=160×0.6+(x-160)×(0.6+0.1)=0.7x-16.
y与x的函数表达式也可以合起来表示为
(2)画出这个函数的图象;
/元
/kW·h
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
当x=150时,y=0.6×150=90,即3月份的电费为90元.
当x=200时,y=0.7×200-16=124,即4月份的电费为124元.
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
【教材P134页】
(1)分别写出y1,y2与x之间的函数表达式;
解:小明所用时间为xh,由“路程=速度×时间”可知y1=
8x,自变量x的取值范围是0≤x≤5.
由于小红比小明晚出发2h,因此小红所用时间为(x-2)h.
从而
y2=40(x-2),
自变量x的取值范围是2≤x≤3.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
/元
/h
l
小明y1=8x
小红y2=40(x-2)
过点M(0,40)作射线l与x轴平行,它先与射线y2=40(x-2)相交,这表明小红先到达乙地.
练习
1.某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8元/天,以后每天收0.5元.
求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式.
解:当0≤t≤2时,y=0.8t
.
当t>2时,y=0.8×2+0.5×(t-2)=0.5t+0.6.
租金y(元)与时间t(天)之间的函数表达式为
【教材P134页】
2.
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36/min;
B方案:零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300
min,他选择哪种付费方式比较合算?
【教材P134页】
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
解:A方案:y
=
25+0.36t(t≥0)
,
B方案:y
=
0.5t(t≥0)
.
(2)分别画出这两个函数的图象;
y
=
25+0.36t(t≥0)
y
=
0.5t(t≥0)
/元
t/min
(3)若林先生每月通话300
min,他选择哪种付费方式比较合算?
解:当t=300时,
A方案:y=25+0.36t=25+0.36×300=133(元);
B方案:y=0.5t=0.5×300=150(元).
150>133,所以此时采用A方案比较合算.
随堂练习
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量(
)
A.小于4件
B.大于4件
C.等于4件
D.大于或等于4件
B
2.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与长跑时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行______米的长跑训练,在0(2)求甲距终点的路程y(米)和跑步时间t(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在155000
甲
(2)解:设一次函数的表达式为y=kx+b,
由于点A(0,
5000),B(20,
0)都在一次函数图像上,将这两点坐标带入表达式,得
k·0
+
b
=
5000,
k·20
+
b
=
0.
解得k=-250,b=5000.
因此所求一次函数的解析式为y=-250x+5000
(3)解:当x=15时,由图象可知乙距离终点2000m,
甲距离终点-250×15+5000=1250m.
两人相距2000-1250=750(m).
在15一次函数的应用
对分段函数图像的理解及运用
建立一次函数模型解决实际问题
课堂小结
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
利用一次函数解决实际问题
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
复习回顾
1.一次函数的表达式为:
y=kx+b(k≠0)
2.待定系数法求一次函数表达式的步骤:
(1)设出一次函数表达式:
y=kx+b(k≠0)
(2)利用给定两点建立二元一次方程组:
(3)解二元一次方程组,得k和b的值,代入表达式即可.
某地为保护环境,鼓励节约用电,实行阶梯电价制度.
规定每户居民每月用电量不超过160kW·h,则按0.6元/(kW·h)收费;若超过160kW·h,则超出部分每1kW·h加收0.1元.
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
(2)画出这个函数的图象;
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
探索新知
(1)写出某户居民某月应缴纳的电费y(元)与用电量x(kW·h)之间的函数表达式;
解:电费与用电量相关.
当0≤x≤160时,y=0.6x;
当x>160时,
y=160×0.6+(x-160)×(0.6+0.1)=0.7x-16.
y与x的函数表达式也可以合起来表示为
(2)画出这个函数的图象;
/元
/kW·h
(3)小王家3月份,4月份分别用电150kW·h和200kW·h,应缴纳电费各多少元?
当x=150时,y=0.6×150=90,即3月份的电费为90元.
当x=200时,y=0.7×200-16=124,即4月份的电费为124元.
甲、乙两地相距40km,小明8:00点骑自行车由甲地去乙地,平均车速为8km/h;小红10:00坐公共汽车也由甲地去乙地,平均车速为40km/h.设小明所用的时间为x(h),小明与甲地的距离为y1(km),小红离甲地的距离为y2(km).
(1)分别写出y1,y2与x之间的函数表达式;
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
【教材P134页】
(1)分别写出y1,y2与x之间的函数表达式;
解:小明所用时间为xh,由“路程=速度×时间”可知y1=
8x,自变量x的取值范围是0≤x≤5.
由于小红比小明晚出发2h,因此小红所用时间为(x-2)h.
从而
y2=40(x-2),
自变量x的取值范围是2≤x≤3.
(2)在同一个直角坐标系中,画出这两个函数的图象,并指出谁先到达乙地.
/元
/h
l
小明y1=8x
小红y2=40(x-2)
过点M(0,40)作射线l与x轴平行,它先与射线y2=40(x-2)相交,这表明小红先到达乙地.
练习
1.某音像店对外出租光盘的收费标准是:每张光盘在出租后头两天的租金为0.8元/天,以后每天收0.5元.
求一张光盘在租出后第n天的租金y(元)与时间t(天)之间的函数表达式.
解:当0≤t≤2时,y=0.8t
.
当t>2时,y=0.8×2+0.5×(t-2)=0.5t+0.6.
租金y(元)与时间t(天)之间的函数表达式为
【教材P134页】
2.
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费25元,另收通话费为0.36/min;
B方案:零月租费,通话费为0.5元/min.
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
(2)分别画出这两个函数的图象;
(3)若林先生每月通话300
min,他选择哪种付费方式比较合算?
【教材P134页】
(1)试写出A,B两种方案所付话费y(元)与通话时间t(min)之间的函数表达式;
解:A方案:y
=
25+0.36t(t≥0)
,
B方案:y
=
0.5t(t≥0)
.
(2)分别画出这两个函数的图象;
y
=
25+0.36t(t≥0)
y
=
0.5t(t≥0)
/元
t/min
(3)若林先生每月通话300
min,他选择哪种付费方式比较合算?
解:当t=300时,
A方案:y=25+0.36t=25+0.36×300=133(元);
B方案:y=0.5t=0.5×300=150(元).
150>133,所以此时采用A方案比较合算.
随堂练习
1.如图,l1反映某公司产品的销售收入与销售量的关系,l2反映该公司产品的销售成本与销售量的关系,根据图象判断该公司盈利时的销售量(
)
A.小于4件
B.大于4件
C.等于4件
D.大于或等于4件
B
2.甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与长跑时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行______米的长跑训练,在0
(3)当x=15时,两人相距多少米?在15
甲
(2)解:设一次函数的表达式为y=kx+b,
由于点A(0,
5000),B(20,
0)都在一次函数图像上,将这两点坐标带入表达式,得
k·0
+
b
=
5000,
k·20
+
b
=
0.
解得k=-250,b=5000.
因此所求一次函数的解析式为y=-250x+5000
(3)解:当x=15时,由图象可知乙距离终点2000m,
甲距离终点-250×15+5000=1250m.
两人相距2000-1250=750(m).
在15
对分段函数图像的理解及运用
建立一次函数模型解决实际问题
课堂小结
课堂小结
1.
说一说本节课的收获。
2.
你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
