第4章 一次函数 小结与复习 课件(共28张PPT)
文档属性
| 名称 | 第4章 一次函数 小结与复习 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
小结与复习
第4章 一次函数
湘教版·八年级数学下册 上课课件
学习目标
【知识与技能】
使学生理解一次函数的意义,掌握根据条件确定一次函数表达式的方法,会画一次函数图象.探究并掌握一次函数性质,并用之解决实际问题.
【过程与方法】
通过例题讲解,学会一次函数性质及应用.
【情感态度】
体会函数作为数学模型在分析解决实际问题中的重要作用.
【教学重点】
应用一次函数的概念、图象和性质解题.
【教学难点】
一次函数在实际问题中的应用.
知识框图
变量
函数
函数的表示法
一次函数
列表法
图像法
公式法
一次函数的图像
用待定系数法确定一次函数的表达式
一次函数的应用
知识回顾
1.一次函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k_____),那么y叫做x的一次函数.
kx+b
≠0
特别地,当b____时,函数y=____(k____)叫做正比例函数.
kx
=0
≠0
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,
⑵比例系数_____.
1
≠0
例1.若y=(m-1)x|m|+1是一次函数,则m的值为______.
【解析】本题考查一次函数的概念.由一次函数的概念可知解析式中自变量x的次数是1次,故|m|=1,所以m=±1,又因为m-1≠0,所以m=-1.
-1
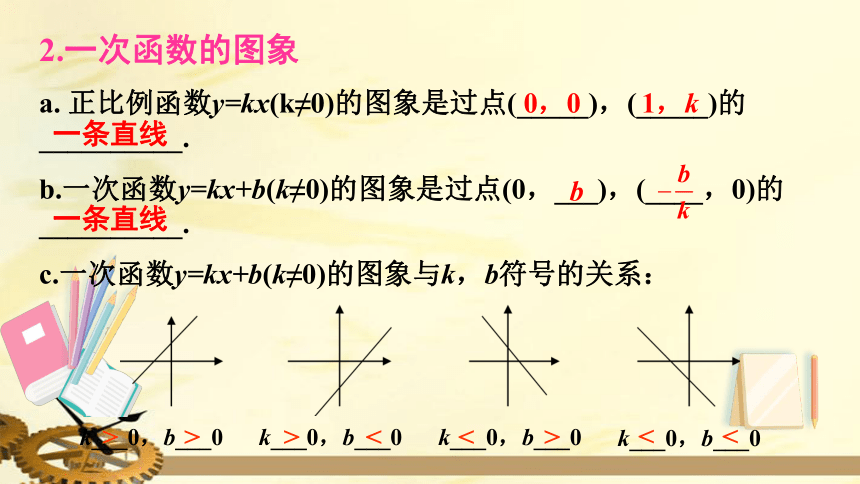
2.一次函数的图象
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(_____)的__________.
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________.
0,0
1,k
一条直线
b
一条直线
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
>
>
<
<
>
<
<
例2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
【解析】根据每段中离家的距离随时间的变化情况即可进行判断,故选B.
B
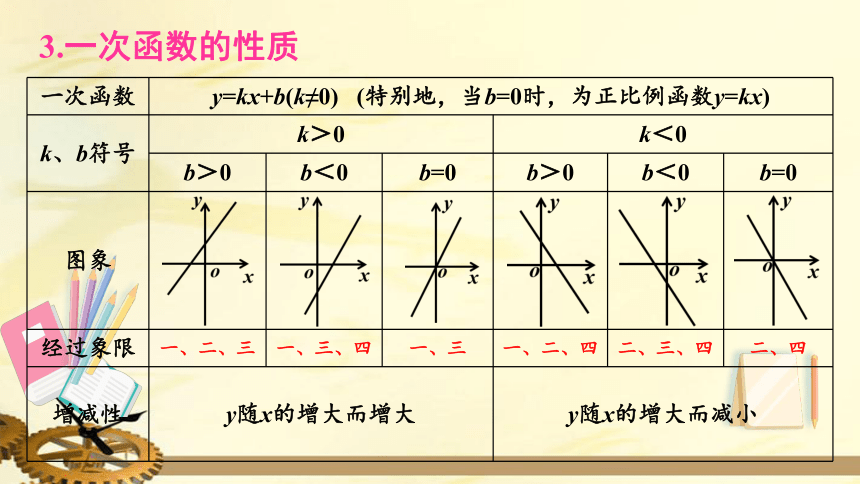
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 3.一次函数的性质
例3. (1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
【解析】(1)因为k=2>0,所以由正比例函数的性质可知,它的图象经过第一、三象限,y随x的增大而增大;(2)y=(2m-1)xm -3是正比例函数的条件是m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这些条件得:当m2-3=1,2m-1<0时, y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,故(1)一、三;增大;(2)-2.
一、三
增大
-2
4.一次函数的应用
(1)待定系数法:
①设这个函数表达式为y=kx+b;
②把已知点的坐标x,y的对应值代入解析式列出方程组;
③解这个二元一次方程组,求出k、b的值;
④把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
(2)利用一次函数解决实际问题:
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.将验证并化简函数表达式,得出问题的变化规律.
例4.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:货车的速度V货=300÷5=60(千米/时),由图象可知货车比轿车迟到0.5小时,∴此时货车距乙地的路程为0.5×60=30(千米);
(2)求线段CD对应的函数解析式.
解:设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,∴2.5k+b=80,4.5k+b=300,解得k=110,b=-195.
∴CD段函数解析式为:y=110x-195(2.5≤x≤4.5);
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,∵v货车=60千米/时,v轿车=300-804.5-2.5=110(千米/时)
∴110(x-4.5)+60x=300,解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
随堂练习
1.某型号体温计中,刻度为35 ℃处,水银柱长2.5 cm.体温每升高1 ℃,水银柱就伸长0.7 cm.
(1)求水银柱长y(cm) 随体温x(℃) 而变化的函数表达式,其中35≤x≤42. 这是不是一次函数?画出它的图象.
(2)分别求当体温为37 ℃,38.6 ℃时,水银柱长多少?
(1)解:y=2.5+(x-35)·0.7=0.7x-22(35≤x≤42),是一次函数.
(2)解:当x=37时,y=3.9;
当x=38.6时,y=5.02.
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
解:与x轴的交点分别为(-6,0),( ,0),( ,0).
3.某公司急需租一辆汽车,甲汽车出租公司的出租条件为每千米的租车费为2 元,乙汽车出租公司的条件是每月需支付固定租金800 元,另外每千米的租车费为1.2 元. 若设汽车行驶路程为x(km),租用甲公司的费用为y1(元),租用乙公司的费用为y2(元).
(1)分别写出y1,y2随x而变化的函数表达式;
(2)在1 个月内,当汽车行驶路程超过多少千米时, 租用乙公司的汽车较合算?
(1)解:y1=2x(x≥0);y2=800+1.2x (x≥0)
y1=2x
y2=800+1.2x
(2)解:分别画出函数y1=2x(x≥0)与y2=800+1.2x (x≥0)图像如下图所示,由图象可知当汽车行驶路程超过1100km时, 租用乙公司的汽车较合算.
4.某城市的一种出租汽车,当行驶路程小于3 km时,车费都为10 元;大于或等于3 km,但小于15 km时,超过3 km 的那部分路程每千米收费1.6 元;大于或等于15 km 时,超过15 km 的那部分每千米收费2.4元. 乘客为了估算应付的车费, 需要一个较简单的计费公式.
(1)你能给出估算车费y(元)与行驶路程x(km)之间的函数表达式吗?
解:由题意得出:当行驶路小于3km时,车费都为10元;则y=10(0<x<3);当大于或等于3km但小于15km时,超过3km的那部分路程每千米收费1.5元;则y=10+1.6(x-3)(3≤x<15);当大于或等于15km时,超过15km的那部分每千米收费2.5元,则y=10+1.6(15-3)+2.4(x-15)=29.2+2.4(x-15)(x≥15),
综上所述
(2)画出这个函数的图象;
(3)当行驶路程为30 km时, 估算车费是多少?
解:当行驶路程为35km时,车费是:
29.2+2.4×(30-15)=65.2(元).
答:当行驶路程为30 km时, 估算车费是65.2元.
课堂小结
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
小结与复习
第4章 一次函数
湘教版·八年级数学下册 上课课件
学习目标
【知识与技能】
使学生理解一次函数的意义,掌握根据条件确定一次函数表达式的方法,会画一次函数图象.探究并掌握一次函数性质,并用之解决实际问题.
【过程与方法】
通过例题讲解,学会一次函数性质及应用.
【情感态度】
体会函数作为数学模型在分析解决实际问题中的重要作用.
【教学重点】
应用一次函数的概念、图象和性质解题.
【教学难点】
一次函数在实际问题中的应用.
知识框图
变量
函数
函数的表示法
一次函数
列表法
图像法
公式法
一次函数的图像
用待定系数法确定一次函数的表达式
一次函数的应用
知识回顾
1.一次函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k_____),那么y叫做x的一次函数.
kx+b
≠0
特别地,当b____时,函数y=____(k____)叫做正比例函数.
kx
=0
≠0
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,
⑵比例系数_____.
1
≠0
例1.若y=(m-1)x|m|+1是一次函数,则m的值为______.
【解析】本题考查一次函数的概念.由一次函数的概念可知解析式中自变量x的次数是1次,故|m|=1,所以m=±1,又因为m-1≠0,所以m=-1.
-1
2.一次函数的图象
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(_____)的__________.
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________.
0,0
1,k
一条直线
b
一条直线
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
k___0,b___0
k___0,b___0
k___0,b___0
k___0,b___0
>
>
>
<
<
>
<
<
例2.某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
【解析】根据每段中离家的距离随时间的变化情况即可进行判断,故选B.
B
一次函数 y=kx+b(k≠0) (特别地,当b=0时,为正比例函数y=kx) k、b符号 k>0 k<0 b>0 b<0 b=0 b>0 b<0 b=0
图象
经过象限 一、二、三 一、三、四 一、三 一、二、四 二、三、四 二、四
增减性 y随x的增大而增大 y随x的增大而减小 3.一次函数的性质
例3. (1)正比例函数y=2x的图象经过第_______象限,y随x的增大而______;
(2)已知y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,则m的值是_____.
【解析】(1)因为k=2>0,所以由正比例函数的性质可知,它的图象经过第一、三象限,y随x的增大而增大;(2)y=(2m-1)xm -3是正比例函数的条件是m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这些条件得:当m2-3=1,2m-1<0时, y=(2m-1)xm -3是正比例函数,且y随x的增大而减小,故(1)一、三;增大;(2)-2.
一、三
增大
-2
4.一次函数的应用
(1)待定系数法:
①设这个函数表达式为y=kx+b;
②把已知点的坐标x,y的对应值代入解析式列出方程组;
③解这个二元一次方程组,求出k、b的值;
④把所求出k、b的值代入y=kx+b中,可具体写出一次函数的表达式.
即:一设二列三解四还原.
(2)利用一次函数解决实际问题:
通过建立函数模型,对变量的变化情况进行预测问题的解题步骤:
1.分析数据,找出自变量和因变量,发现对应关系;
2.抽象出函数表达式;
3.将验证并化简函数表达式,得出问题的变化规律.
例4.甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
解:根据图象信息:货车的速度V货=300÷5=60(千米/时),由图象可知货车比轿车迟到0.5小时,∴此时货车距乙地的路程为0.5×60=30(千米);
(2)求线段CD对应的函数解析式.
解:设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,∴2.5k+b=80,4.5k+b=300,解得k=110,b=-195.
∴CD段函数解析式为:y=110x-195(2.5≤x≤4.5);
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:设轿车从甲地出发x小时后再与货车相遇,∵v货车=60千米/时,v轿车=300-804.5-2.5=110(千米/时)
∴110(x-4.5)+60x=300,解得x≈4.68(小时).
答:轿车从甲地出发约4.68小时后再与货车相遇.
随堂练习
1.某型号体温计中,刻度为35 ℃处,水银柱长2.5 cm.体温每升高1 ℃,水银柱就伸长0.7 cm.
(1)求水银柱长y(cm) 随体温x(℃) 而变化的函数表达式,其中35≤x≤42. 这是不是一次函数?画出它的图象.
(2)分别求当体温为37 ℃,38.6 ℃时,水银柱长多少?
(1)解:y=2.5+(x-35)·0.7=0.7x-22(35≤x≤42),是一次函数.
(2)解:当x=37时,y=3.9;
当x=38.6时,y=5.02.
2.在同一直角坐标系中,画出下列一次函数的图象,并利用图象法和公式法分别求出该函数图象与x轴的交点.
解:与x轴的交点分别为(-6,0),( ,0),( ,0).
3.某公司急需租一辆汽车,甲汽车出租公司的出租条件为每千米的租车费为2 元,乙汽车出租公司的条件是每月需支付固定租金800 元,另外每千米的租车费为1.2 元. 若设汽车行驶路程为x(km),租用甲公司的费用为y1(元),租用乙公司的费用为y2(元).
(1)分别写出y1,y2随x而变化的函数表达式;
(2)在1 个月内,当汽车行驶路程超过多少千米时, 租用乙公司的汽车较合算?
(1)解:y1=2x(x≥0);y2=800+1.2x (x≥0)
y1=2x
y2=800+1.2x
(2)解:分别画出函数y1=2x(x≥0)与y2=800+1.2x (x≥0)图像如下图所示,由图象可知当汽车行驶路程超过1100km时, 租用乙公司的汽车较合算.
4.某城市的一种出租汽车,当行驶路程小于3 km时,车费都为10 元;大于或等于3 km,但小于15 km时,超过3 km 的那部分路程每千米收费1.6 元;大于或等于15 km 时,超过15 km 的那部分每千米收费2.4元. 乘客为了估算应付的车费, 需要一个较简单的计费公式.
(1)你能给出估算车费y(元)与行驶路程x(km)之间的函数表达式吗?
解:由题意得出:当行驶路小于3km时,车费都为10元;则y=10(0<x<3);当大于或等于3km但小于15km时,超过3km的那部分路程每千米收费1.5元;则y=10+1.6(x-3)(3≤x<15);当大于或等于15km时,超过15km的那部分每千米收费2.5元,则y=10+1.6(15-3)+2.4(x-15)=29.2+2.4(x-15)(x≥15),
综上所述
(2)画出这个函数的图象;
(3)当行驶路程为30 km时, 估算车费是多少?
解:当行驶路程为35km时,车费是:
29.2+2.4×(30-15)=65.2(元).
答:当行驶路程为30 km时, 估算车费是65.2元.
课堂小结
1. 说一说本节课的收获。
2. 你还存在哪些疑惑?
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
