2020-2021学年人教版八年级数学下册 第二十章 数据的分析 章末训练(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册 第二十章 数据的分析 章末训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 565.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览




文档简介
人教版八年级数学下册 第二十章 数据的分析 章末训练
一、选择题
1. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示,这些成绩的中位数和众数分别是 ( )
A.96分,98分 B.97分,98分
C.98分,96分 D.97分,96分
2. 今年某市扶贫办对贫困户进行精准扶贫,效果显著.为了解他们后续的收入是否稳定,则工作人员需了解贫困户收入的 ( )
A.方差 B.众数 C.平均数 D.频数
3. 在10,16,40,17,20,50,40这组数据中,中位数是 ( )
A.17 B.20 C.50 D.40
4. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:
调查问卷□ 年 月 日?
你平时最喜欢的一种体育运动项目是( )(单选)
A. B. C. D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是 ( )
A.①②③ B.①③⑤ C.②③④ D.②④⑤
5. 某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:-10,+5,0,+5,0,0,-5,0,+5,+10.则可估计这批食品罐头质量的平均数为 ( )
A.453克 B.454克 C.455克 D.456克
6. 10支不同型号的签字笔的相关信息如下表所示,则这10支签字笔的平均单价是 ( )
A.1.4元/支 B.1.5元/支 C.1.6元/支 D.1.7元/支
7. 某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
8. 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是 ( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
二、填空题
9. 2019年5月28日全国部分宜居城市最高气温的数据如下:
宜居城市 大连 青岛 威海 金华 昆明 三亚
最高气温(℃) 25 28 35 30 26 32
则以上最高气温的中位数为________℃.
10. 某校300名学生参加植树活动,要求每人植树2~5(包含2和5)棵,活动结束后随机抽查了20名学生每人的植树量,并分为四类:A类2棵、B类3棵、C类4棵、D类5棵,将各类的人数绘制成如图所示的不完整的条形统计图.
(1)D类学生有 人;?
(2)估计这300名学生共植树 棵.?
11. 设计调查活动要经历5个重要步骤:①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.但这5个步骤的排序不对,正确排序为 .(填序号)?
12. 学校进行广播体操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是 分.?
13. 跳远训练时,甲、乙两名同学在相同条件下各跳了10次,统计他们的平均成绩都是5.68米,且方差为=0.3,=0.4,则成绩较稳定的是 .?
14. 商店想调查哪种品牌的空调销售量大,用?
来描述较好.某同学的身高在全班45人中排名第23,则他的身高值可看作是全班同学身高值的 .(填“中位数”“众数”或“平均数”)?
15. 某公司要招聘一名职员,根据实际需要,从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试,测试成绩如下表所示.如果将学历、经验和工作态度三项得分按2∶1∶3的比例确定两人的最终得分,并以此为依据确定录用者,那么 将被录用(填“甲”或“乙”).?
16. 某校规定学生的数学学期综合成绩由平时、期中和期末三项成绩按3∶x∶(7-x)的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分、90分和85分,他本学期数学学期综合成绩是88分,则x= .?
三、解答题
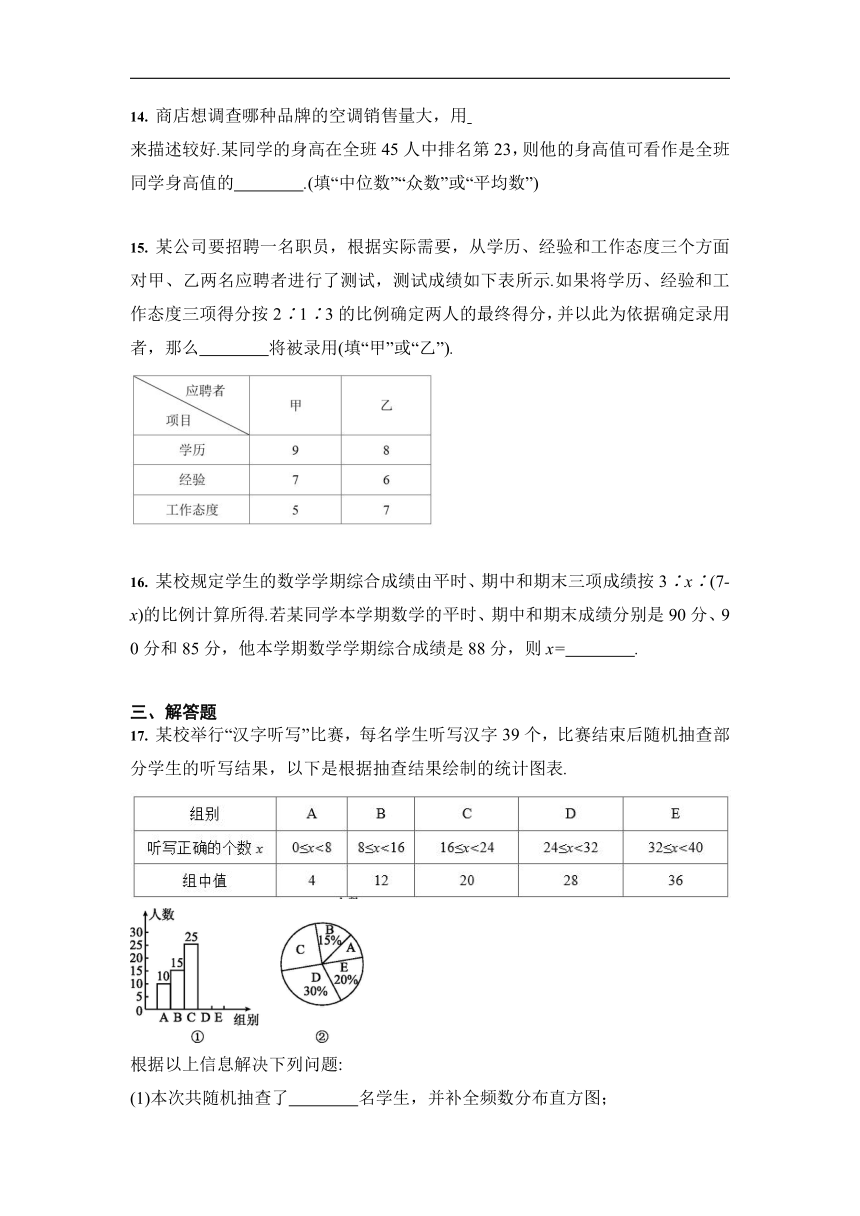
17. 某校举行“汉字听写”比赛,每名学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图表.
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;?
(2)若用组中值代替每组听写正确的个数,则被抽查学生听写正确的个数的平均数是多少?
18. 某班为了从甲、乙两名同学中选出一名班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50名同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分统计表(单位:分)
表2 民主测评得票统计表(单位:张)
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩得分×(1-a)+民主测评得分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)当a在什么范围内时,甲的综合得分高?当a在什么范围内时,乙的综合得分高?
19. 八(1)班同学分成甲、乙两组,开展“社会主义核心价值观”知识竞赛,满分5分,得分均为整数.小马虎根据竞赛成绩,绘制了如图所示的分组成绩条形统计图和全班成绩扇形统计图,经确认,扇形统计图是正确的,条形统计图也只有乙组成绩统计有一处错误.
(1)甲组同学成绩的平均数是 ,中位数是 ,众数是 ;?
(2)指出条形统计图中存在的错误,并求出正确值.
20. 某地区在一次八年级数学质量检测中,有一道满分为8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易程度,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如图所示的两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)a= ,b= ,并把条形统计图补全.?
(2)请估计该地区此题得满分(即8分)的学生人数.
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当021. 某校对八年级甲、乙两班各60名学生进行知识测试,测试完成后分别抽取了12份成绩,整理分析过程如下.
【收集数据】
甲班12名学生测试成绩(单位:分)统计如下:45,59,60,38,57,53,52,58,60,50,43,49;
乙班12名学生测试成绩(单位:分)统计如下:35,55,46,39,54,47,43,57,42,59,60,47.
【整理数据】
按如下分数段整理,描述这两组样本数据:
【分析数据】
两组样本数据的平均数、众数、中位数如下表所示:·
根据以上信息回答下列问题.
(1)a= ,b= ;?
(2)若规定成绩在40分及以上为合格,请估计乙班60名学生中知识测试成绩合格的学生有多少人.
(3)你认为哪个班的学生知识测试成绩的整体水平较好,请说出一条理由.
22. 中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图.
(1)根据图示填写下表;
班级 平均数/分 中位数/分 众数/分
九(1) 85
85
九(2)
80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
{方差公式:s2=[(x1-)2+(x2-)2+…+(xn-)2]}
人教版八年级数学下册 第二十章 数据的分析 章末训练-答案
一、选择题
1. 【答案】A [解析] 由统计图可知:按顺序排列,第13名同学的分数为96分,故中位数为96分;得分人数最多的是98分,共9人,故众数为98分.故选A.
2. 【答案】A
3. 【答案】B
4. 【答案】C
5. 【答案】C [解析] 平均数是454+=454+1=455(克).
6. 【答案】C
7. 【答案】A [解析] 换人前,平均数为
=188(cm),方差为×[(180-188)2+(184-188)2+(188-188)2+(190-188)2+(192-188)2+(194-188)2]=;
换人后,平均数为
=187(cm),方差为×[(180-187)2+(184-187)2+(186-187)2+(188-187)2+(190-187)2+(194-187)2]=.
所以换人后,平均数变小,方差变小.故选A.
8. 【答案】D [解析] 先求出共调查了60人,得分为94分的有12人,得分为98分的有18人,通过计算可知,中位数是96分,平均数为96.4分.
故选D.
二、填空题
9. 【答案】29 【解析】将这组数据按从小到大的顺序排列为25,26,28,30,32,35.数据共6个,是偶数,则中位数是第3和4个数据的平均数,即中位数为(28+30)÷2=29.
10. 【答案】(1)2 (2)990 [解析] (1)由条形统计图,知A,B,C三类的人数分别为4,8,6.
因为20-(4+8+6)=2,
所以D类学生有2人.
(2)样本的平均数==3.3(棵),
因为300×3.3=990(棵),
所以估计300名学生共植树990棵.
11. 【答案】②①④⑤③
12. 【答案】9.1 [解析] 根据加权平均数公式,有=×(8×5+9×8+10×7)=×(40+72+70)=×182=9.1(分).故答案为9.1.
13. 【答案】甲 [解析] 方差越小,数据越稳定.
14. 【答案】众数 中位数
15. 【答案】乙
16. 【答案】3 [解析] 依题意可列方程×[90×3+90x+85×(7-x)]=88,解得x=3.
三、解答题
17. 【答案】
解:(1)由统计图可知,B组有15人,占被抽查学生的15%,所以被抽查的学生人数=15÷15%=100(人).D组人数=100×30%=30(人),E组人数=100×20%=20(人).
补全频数分布直方图如图所示.
(2)因为本次共抽查了100名学生,其中A组学生有10人,C组学生有25人,所以A组学生占抽查总人数的百分比为×100%=10%,C组学生占抽查总人数的百分比为×100%=25%.
4×10%+12×15%+20×25%+28×30%+36×20%=22.8(个).
所以被抽查学生听写正确的个数的平均数是22.8个.
18. 【答案】
解:(1)甲的演讲答辩得分为=92(分),
甲的民主测评得分为40×2+7×1+3×0=87(分).
当a=0.6时,甲的综合得分为
92× (1-0.6)+87×0.6=36.8+52.2=89(分).
(2)因为乙的演讲答辩得分为=89(分),
乙的民主测评得分为42×2+4×1+4×0=88(分),
所以乙的综合得分为89(1-a)+88a.
由(1)知,甲的综合得分为92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,a<0.75.
又因为0.5≤a≤0.8,
所以当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,a>0.75.
又因为0.5≤a≤0.8,
所以当0.7519. 【答案】
解:(1)甲组同学成绩的平均数=(2×3+3×7+4×6+5×4)÷20=3.55(分).
中位数=(3+4)÷2=3.5(分),众数是3分.
故答案为3.55分,3.5分,3分.
(2)乙组得5分的人数统计有误.
理由:由条形统计图和扇形统计图的对应值可得,2÷5%=40,(3+2)÷12.5%=40,(7+5)÷30%=40,(6+8)÷35%=40,(4+4)÷17.5%≠40,故乙组得5分的人数统计有误.
正确人数应为40×17.5%-4=3(人).
20. 【答案】
解:(1)a=25,b=20,补全条形统计图如图.
(2)由(1)可知,得满分的占20%,
所以估计该地区此题得满分(即8分)的学生人数是4500×20%=900(人).
(3)由题意可得
L===0.575.
因为0.575处于0.4与0.7之间,
所以此题对于该地区的八年级学生来说属于中等难度试题.
21. 【答案】
解:(1)60 47
(2)60×=50(人).
即乙班60名学生中知识测试成绩合格的学生有50人.
(3)甲班的学生知识测试成绩的整体水平较好.
理由:因为甲班平均数>乙班平均数,
所以甲班的学生知识测试成绩的整体水平较好(理由合理即可).
22. 【答案】
解:(1)填表如下:
班级 平均数/分 中位数/分 众数/分
九(1) 85 85 85
九(2) 85 80 100
(2)九(1)班成绩好些.因为两个班级的平均数都相同,九(1)班的中位数高,所以在平均数相同的情况下中位数高的九(1)班成绩好些.
(3)s=
=70,
s=
=160.
一、选择题
1. 在光明中学组织的全校师生迎“五四”诗词大赛中,来自不同年级的25名参赛同学的得分情况如图所示,这些成绩的中位数和众数分别是 ( )
A.96分,98分 B.97分,98分
C.98分,96分 D.97分,96分
2. 今年某市扶贫办对贫困户进行精准扶贫,效果显著.为了解他们后续的收入是否稳定,则工作人员需了解贫困户收入的 ( )
A.方差 B.众数 C.平均数 D.频数
3. 在10,16,40,17,20,50,40这组数据中,中位数是 ( )
A.17 B.20 C.50 D.40
4. 某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如下尚不完整的调查问卷:
调查问卷□ 年 月 日?
你平时最喜欢的一种体育运动项目是( )(单选)
A. B. C. D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是 ( )
A.①②③ B.①③⑤ C.②③④ D.②④⑤
5. 某外贸公司要出口一批食品罐头,标准质量为每听454克,现抽取10听样品进行检测,它们的质量与标准质量的差值(单位:克)如下:-10,+5,0,+5,0,0,-5,0,+5,+10.则可估计这批食品罐头质量的平均数为 ( )
A.453克 B.454克 C.455克 D.456克
6. 10支不同型号的签字笔的相关信息如下表所示,则这10支签字笔的平均单价是 ( )
A.1.4元/支 B.1.5元/支 C.1.6元/支 D.1.7元/支
7. 某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员的身高 ( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
8. 某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是 ( )
A.94分,96分 B.96分,96分
C.94分,96.4分 D.96分,96.4分
二、填空题
9. 2019年5月28日全国部分宜居城市最高气温的数据如下:
宜居城市 大连 青岛 威海 金华 昆明 三亚
最高气温(℃) 25 28 35 30 26 32
则以上最高气温的中位数为________℃.
10. 某校300名学生参加植树活动,要求每人植树2~5(包含2和5)棵,活动结束后随机抽查了20名学生每人的植树量,并分为四类:A类2棵、B类3棵、C类4棵、D类5棵,将各类的人数绘制成如图所示的不完整的条形统计图.
(1)D类学生有 人;?
(2)估计这300名学生共植树 棵.?
11. 设计调查活动要经历5个重要步骤:①收集数据;②设计调查问卷;③用样本估计总体;④整理数据;⑤分析数据.但这5个步骤的排序不对,正确排序为 .(填序号)?
12. 学校进行广播体操比赛,如图是20位评委给某班的评分情况统计图,则该班的平均得分是 分.?
13. 跳远训练时,甲、乙两名同学在相同条件下各跳了10次,统计他们的平均成绩都是5.68米,且方差为=0.3,=0.4,则成绩较稳定的是 .?
14. 商店想调查哪种品牌的空调销售量大,用?
来描述较好.某同学的身高在全班45人中排名第23,则他的身高值可看作是全班同学身高值的 .(填“中位数”“众数”或“平均数”)?
15. 某公司要招聘一名职员,根据实际需要,从学历、经验和工作态度三个方面对甲、乙两名应聘者进行了测试,测试成绩如下表所示.如果将学历、经验和工作态度三项得分按2∶1∶3的比例确定两人的最终得分,并以此为依据确定录用者,那么 将被录用(填“甲”或“乙”).?
16. 某校规定学生的数学学期综合成绩由平时、期中和期末三项成绩按3∶x∶(7-x)的比例计算所得.若某同学本学期数学的平时、期中和期末成绩分别是90分、90分和85分,他本学期数学学期综合成绩是88分,则x= .?
三、解答题
17. 某校举行“汉字听写”比赛,每名学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图表.
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;?
(2)若用组中值代替每组听写正确的个数,则被抽查学生听写正确的个数的平均数是多少?
18. 某班为了从甲、乙两名同学中选出一名班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50名同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分统计表(单位:分)
表2 民主测评得票统计表(单位:张)
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩得分×(1-a)+民主测评得分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)当a在什么范围内时,甲的综合得分高?当a在什么范围内时,乙的综合得分高?
19. 八(1)班同学分成甲、乙两组,开展“社会主义核心价值观”知识竞赛,满分5分,得分均为整数.小马虎根据竞赛成绩,绘制了如图所示的分组成绩条形统计图和全班成绩扇形统计图,经确认,扇形统计图是正确的,条形统计图也只有乙组成绩统计有一处错误.
(1)甲组同学成绩的平均数是 ,中位数是 ,众数是 ;?
(2)指出条形统计图中存在的错误,并求出正确值.
20. 某地区在一次八年级数学质量检测中,有一道满分为8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易程度,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如图所示的两幅不完整的统计图.
请根据以上信息解答下列问题:
(1)a= ,b= ,并把条形统计图补全.?
(2)请估计该地区此题得满分(即8分)的学生人数.
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0
【收集数据】
甲班12名学生测试成绩(单位:分)统计如下:45,59,60,38,57,53,52,58,60,50,43,49;
乙班12名学生测试成绩(单位:分)统计如下:35,55,46,39,54,47,43,57,42,59,60,47.
【整理数据】
按如下分数段整理,描述这两组样本数据:
【分析数据】
两组样本数据的平均数、众数、中位数如下表所示:·
根据以上信息回答下列问题.
(1)a= ,b= ;?
(2)若规定成绩在40分及以上为合格,请估计乙班60名学生中知识测试成绩合格的学生有多少人.
(3)你认为哪个班的学生知识测试成绩的整体水平较好,请说出一条理由.
22. 中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图.
(1)根据图示填写下表;
班级 平均数/分 中位数/分 众数/分
九(1) 85
85
九(2)
80
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.
{方差公式:s2=[(x1-)2+(x2-)2+…+(xn-)2]}
人教版八年级数学下册 第二十章 数据的分析 章末训练-答案
一、选择题
1. 【答案】A [解析] 由统计图可知:按顺序排列,第13名同学的分数为96分,故中位数为96分;得分人数最多的是98分,共9人,故众数为98分.故选A.
2. 【答案】A
3. 【答案】B
4. 【答案】C
5. 【答案】C [解析] 平均数是454+=454+1=455(克).
6. 【答案】C
7. 【答案】A [解析] 换人前,平均数为
=188(cm),方差为×[(180-188)2+(184-188)2+(188-188)2+(190-188)2+(192-188)2+(194-188)2]=;
换人后,平均数为
=187(cm),方差为×[(180-187)2+(184-187)2+(186-187)2+(188-187)2+(190-187)2+(194-187)2]=.
所以换人后,平均数变小,方差变小.故选A.
8. 【答案】D [解析] 先求出共调查了60人,得分为94分的有12人,得分为98分的有18人,通过计算可知,中位数是96分,平均数为96.4分.
故选D.
二、填空题
9. 【答案】29 【解析】将这组数据按从小到大的顺序排列为25,26,28,30,32,35.数据共6个,是偶数,则中位数是第3和4个数据的平均数,即中位数为(28+30)÷2=29.
10. 【答案】(1)2 (2)990 [解析] (1)由条形统计图,知A,B,C三类的人数分别为4,8,6.
因为20-(4+8+6)=2,
所以D类学生有2人.
(2)样本的平均数==3.3(棵),
因为300×3.3=990(棵),
所以估计300名学生共植树990棵.
11. 【答案】②①④⑤③
12. 【答案】9.1 [解析] 根据加权平均数公式,有=×(8×5+9×8+10×7)=×(40+72+70)=×182=9.1(分).故答案为9.1.
13. 【答案】甲 [解析] 方差越小,数据越稳定.
14. 【答案】众数 中位数
15. 【答案】乙
16. 【答案】3 [解析] 依题意可列方程×[90×3+90x+85×(7-x)]=88,解得x=3.
三、解答题
17. 【答案】
解:(1)由统计图可知,B组有15人,占被抽查学生的15%,所以被抽查的学生人数=15÷15%=100(人).D组人数=100×30%=30(人),E组人数=100×20%=20(人).
补全频数分布直方图如图所示.
(2)因为本次共抽查了100名学生,其中A组学生有10人,C组学生有25人,所以A组学生占抽查总人数的百分比为×100%=10%,C组学生占抽查总人数的百分比为×100%=25%.
4×10%+12×15%+20×25%+28×30%+36×20%=22.8(个).
所以被抽查学生听写正确的个数的平均数是22.8个.
18. 【答案】
解:(1)甲的演讲答辩得分为=92(分),
甲的民主测评得分为40×2+7×1+3×0=87(分).
当a=0.6时,甲的综合得分为
92× (1-0.6)+87×0.6=36.8+52.2=89(分).
(2)因为乙的演讲答辩得分为=89(分),
乙的民主测评得分为42×2+4×1+4×0=88(分),
所以乙的综合得分为89(1-a)+88a.
由(1)知,甲的综合得分为92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,a<0.75.
又因为0.5≤a≤0.8,
所以当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,a>0.75.
又因为0.5≤a≤0.8,
所以当0.75
解:(1)甲组同学成绩的平均数=(2×3+3×7+4×6+5×4)÷20=3.55(分).
中位数=(3+4)÷2=3.5(分),众数是3分.
故答案为3.55分,3.5分,3分.
(2)乙组得5分的人数统计有误.
理由:由条形统计图和扇形统计图的对应值可得,2÷5%=40,(3+2)÷12.5%=40,(7+5)÷30%=40,(6+8)÷35%=40,(4+4)÷17.5%≠40,故乙组得5分的人数统计有误.
正确人数应为40×17.5%-4=3(人).
20. 【答案】
解:(1)a=25,b=20,补全条形统计图如图.
(2)由(1)可知,得满分的占20%,
所以估计该地区此题得满分(即8分)的学生人数是4500×20%=900(人).
(3)由题意可得
L===0.575.
因为0.575处于0.4与0.7之间,
所以此题对于该地区的八年级学生来说属于中等难度试题.
21. 【答案】
解:(1)60 47
(2)60×=50(人).
即乙班60名学生中知识测试成绩合格的学生有50人.
(3)甲班的学生知识测试成绩的整体水平较好.
理由:因为甲班平均数>乙班平均数,
所以甲班的学生知识测试成绩的整体水平较好(理由合理即可).
22. 【答案】
解:(1)填表如下:
班级 平均数/分 中位数/分 众数/分
九(1) 85 85 85
九(2) 85 80 100
(2)九(1)班成绩好些.因为两个班级的平均数都相同,九(1)班的中位数高,所以在平均数相同的情况下中位数高的九(1)班成绩好些.
(3)s=
=70,
s=
=160.
