4.3 一次函数的图像(第1课时) 正比例函数的图象和性质 课件(共26张PPT)
文档属性
| 名称 | 4.3 一次函数的图像(第1课时) 正比例函数的图象和性质 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
正比例函数的图象和性质
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生能用两点法画出正比例函数的图象.
2.初步了解正比例函数图象的性质.
【过程与方法】
通过画正比例函数的图象,探索正比例函数图象的性质,培养观察能力,体会用数形结合的方式思考问题.
【情感态度】
1.在学习中学会主动参与、积极思维,并获得成功的体验,锻炼克服困难的意志.
2.通过动手操作,培养严谨的学习态度,并养成善于观察、善于归纳的学习习惯.
【教学重点】
正确理解正比例函数的图象及性质.
【教学难点】
通过对正比例函数图象的观察,发现正比例函数图象的性质.
复习回顾
一次函数的定义:
若两个变量x,y间的关系式可以表示成y=kx+b(k、b为常数,k≠0)的形式,则称y是x是一次函数,其中x为自变量,y为因变量.
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
探索新知
画正比例函数y=2x的图像.
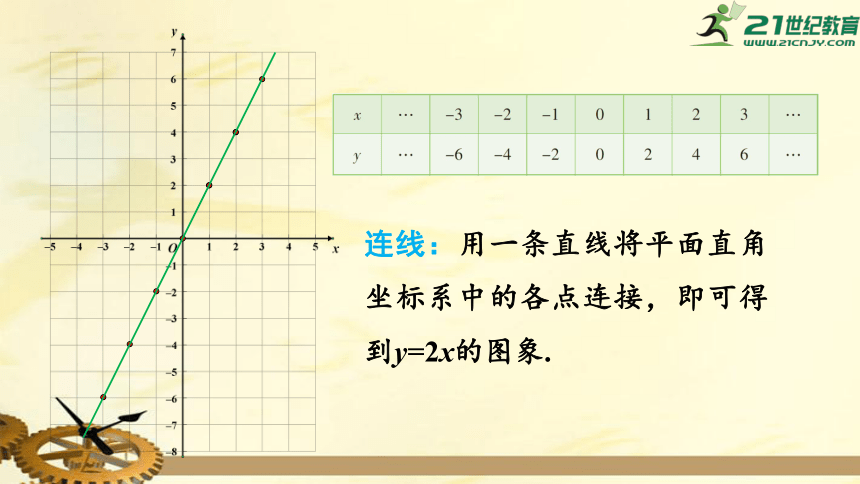
列表:先取自变量x的一些值,计算出相应的函数值,列成表格如下:
描点:建立平面直角坐标系,以自变量值为横坐标,相应的函数值为纵坐标,描出这些点,如图:
连线:用一条直线将平面直角坐标系中的各点连接,即可得到y=2x的图象.
总结归纳
画函数图象的一般步骤:
①
列表
②
描点
③
连线
能够简化吗?
类似地,数学上已经证明:正比例函数y=kx(k为常数,k≠0)的图象是一条直线.由于两点确定一条直线,因此画正比例函数的图象,只要描出图象上的两个点,然后过这两点作一条直线即可.我们常常把这条直线叫作“直线y=kx”.
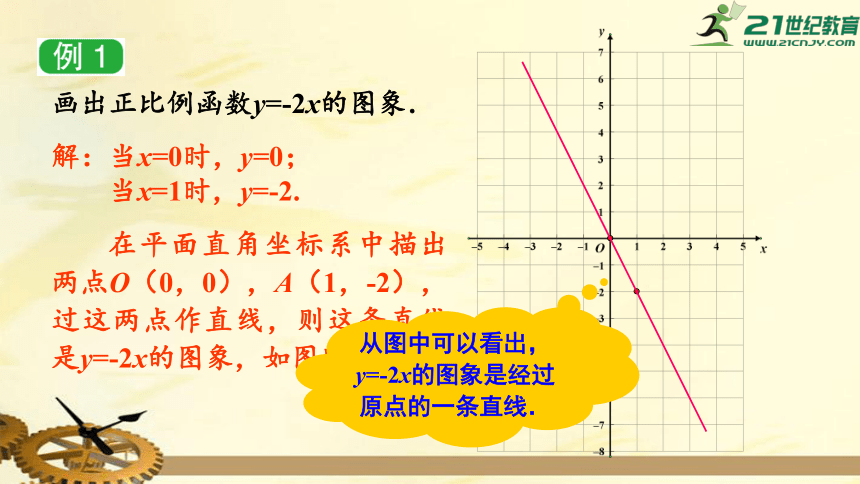
画出正比例函数y=-2x的图象.
解:当x=0时,y=0;
当x=1时,y=-2.
在平面直角坐标系中描出两点O(0,0),A(1,-2),过这两点作直线,则这条直线是y=-2x的图象,如图所示.
从图中可以看出,
y=-2x的图象是经过原点的一条直线.
y=-2x
y=2x
相同点:两图象都是经过原点的一条直线.
思考:观察这两个函数图象有什么相同点?有什么不同点?
y=-2x
y=2x
不同点:函数y=2x的图象经过第________象限,从左向右___
____________,函数y=-2x的图象经过第________象限.从左向右____________.
一、三
呈上升状态
二、四
呈下降状态
在平面直角坐标系中(如图),
任意画一个正比例函数y=kx(k为常数,k≠0)的图象,它是经过原点的一条直线吗?
总结归纳
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0)
经过的象限
k>0
第一、三象限
k<0
第二、四象限
某国家森林公园的一个旅游景点的电梯运行时,以3m/s的速度上升,运行总高度为300m.
(1)求电梯运行高度h(m)随运行时间t(s)而变化的函数表达式;
解:由路程=速度×时间,可知h=3t,0≤t≤100.
(2)画出这个函数的图象.
解:当t=0时,h=0;当t=100时,h=300,在平面直角坐标系中描出两点O(0,0),A(100,300).
过这两点作线段OA,线段OA即函数h=3t(0≤t≤100)的图象,如图所示.
练习
1.画出正比例函数y=
,y=3x的图象,并分别指出其经过哪些象限.
y=3x
解:正比例函数y=
经过二、四象限,正比例函数y=3x经过一、三象限.
2.已知矩形的一边长为6
cm,另一边长为x
cm.面积为y(cm2).
(1)求y随x而变化的函数表达式;
(2)画出该函数的图象;
(3)当x=3,4,5时,y是多少?
解:y=6x
y=6x
当x=3时,y=18;
当x=4时,y=24;
当x=5时,y=30.
随堂练习
1.已知正比例函数y=(1-2m)x的图象经过第二、四象限,则m的取值范围是(
)
A.
m>
B.
m<
C.
m<0
D.
m>0
A
2.
P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,下列判断中,正确的是(
)
A.y1>y2
B.y1C.当x1D.当x1y2
D
3.函数y=-
x的图象是一条经过原点及点(2,____)的直线,这条直线经过第______象限,当x增大时,y随之_______.
-3
二、四
减小
4.一水管向容器为100立方米的空水池注水,注水时间t与注入的水量Q的关系如下表:
t
(分钟)
…
2
4
6
8
10
…
Q
(立方米)
…
4
8
12
16
20
…
(1)求Q与t之间的函数关系式;
(2)求自变量t的取值范围,并画出图象;
(3)当t=40分钟时,求水量Q的值是多少?
解:(1)
Q=2t;
(2)
由题可知0≤Q≤100,即0≤2t≤100,0≤t≤50.
Q=2t
(3)
当t=40时,Q=80.
课堂小结
1.函数与图象之间是一一对应的关系;
2.正比例函数的图象是一条经过原点的直线;
3.作正比例函数图象时,只取原点外的另一个点,就能很快作出.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
正比例函数的图象和性质
第4章
一次函数
湘教版·八年级数学下册
上课课件
学习目标
【知识与技能】
1.使学生能用两点法画出正比例函数的图象.
2.初步了解正比例函数图象的性质.
【过程与方法】
通过画正比例函数的图象,探索正比例函数图象的性质,培养观察能力,体会用数形结合的方式思考问题.
【情感态度】
1.在学习中学会主动参与、积极思维,并获得成功的体验,锻炼克服困难的意志.
2.通过动手操作,培养严谨的学习态度,并养成善于观察、善于归纳的学习习惯.
【教学重点】
正确理解正比例函数的图象及性质.
【教学难点】
通过对正比例函数图象的观察,发现正比例函数图象的性质.
复习回顾
一次函数的定义:
若两个变量x,y间的关系式可以表示成y=kx+b(k、b为常数,k≠0)的形式,则称y是x是一次函数,其中x为自变量,y为因变量.
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
探索新知
画正比例函数y=2x的图像.
列表:先取自变量x的一些值,计算出相应的函数值,列成表格如下:
描点:建立平面直角坐标系,以自变量值为横坐标,相应的函数值为纵坐标,描出这些点,如图:
连线:用一条直线将平面直角坐标系中的各点连接,即可得到y=2x的图象.
总结归纳
画函数图象的一般步骤:
①
列表
②
描点
③
连线
能够简化吗?
类似地,数学上已经证明:正比例函数y=kx(k为常数,k≠0)的图象是一条直线.由于两点确定一条直线,因此画正比例函数的图象,只要描出图象上的两个点,然后过这两点作一条直线即可.我们常常把这条直线叫作“直线y=kx”.
画出正比例函数y=-2x的图象.
解:当x=0时,y=0;
当x=1时,y=-2.
在平面直角坐标系中描出两点O(0,0),A(1,-2),过这两点作直线,则这条直线是y=-2x的图象,如图所示.
从图中可以看出,
y=-2x的图象是经过原点的一条直线.
y=-2x
y=2x
相同点:两图象都是经过原点的一条直线.
思考:观察这两个函数图象有什么相同点?有什么不同点?
y=-2x
y=2x
不同点:函数y=2x的图象经过第________象限,从左向右___
____________,函数y=-2x的图象经过第________象限.从左向右____________.
一、三
呈上升状态
二、四
呈下降状态
在平面直角坐标系中(如图),
任意画一个正比例函数y=kx(k为常数,k≠0)的图象,它是经过原点的一条直线吗?
总结归纳
y=kx
(k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0)
经过的象限
k>0
第一、三象限
k<0
第二、四象限
某国家森林公园的一个旅游景点的电梯运行时,以3m/s的速度上升,运行总高度为300m.
(1)求电梯运行高度h(m)随运行时间t(s)而变化的函数表达式;
解:由路程=速度×时间,可知h=3t,0≤t≤100.
(2)画出这个函数的图象.
解:当t=0时,h=0;当t=100时,h=300,在平面直角坐标系中描出两点O(0,0),A(100,300).
过这两点作线段OA,线段OA即函数h=3t(0≤t≤100)的图象,如图所示.
练习
1.画出正比例函数y=
,y=3x的图象,并分别指出其经过哪些象限.
y=3x
解:正比例函数y=
经过二、四象限,正比例函数y=3x经过一、三象限.
2.已知矩形的一边长为6
cm,另一边长为x
cm.面积为y(cm2).
(1)求y随x而变化的函数表达式;
(2)画出该函数的图象;
(3)当x=3,4,5时,y是多少?
解:y=6x
y=6x
当x=3时,y=18;
当x=4时,y=24;
当x=5时,y=30.
随堂练习
1.已知正比例函数y=(1-2m)x的图象经过第二、四象限,则m的取值范围是(
)
A.
m>
B.
m<
C.
m<0
D.
m>0
A
2.
P1(x1,y1),P2(x2,y2)是正比例函数y=-x图象上的两点,下列判断中,正确的是(
)
A.y1>y2
B.y1
D
3.函数y=-
x的图象是一条经过原点及点(2,____)的直线,这条直线经过第______象限,当x增大时,y随之_______.
-3
二、四
减小
4.一水管向容器为100立方米的空水池注水,注水时间t与注入的水量Q的关系如下表:
t
(分钟)
…
2
4
6
8
10
…
Q
(立方米)
…
4
8
12
16
20
…
(1)求Q与t之间的函数关系式;
(2)求自变量t的取值范围,并画出图象;
(3)当t=40分钟时,求水量Q的值是多少?
解:(1)
Q=2t;
(2)
由题可知0≤Q≤100,即0≤2t≤100,0≤t≤50.
Q=2t
(3)
当t=40时,Q=80.
课堂小结
1.函数与图象之间是一一对应的关系;
2.正比例函数的图象是一条经过原点的直线;
3.作正比例函数图象时,只取原点外的另一个点,就能很快作出.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
