七年级数学复习提纲第13章走进概率

七年级数学复习提纲
第13章 走进概率
学习目标
经历“猜测——实验并收集实验数据——分析实验结果”的活动过程；
能区分确定事件与不确定事件，知道事件发生的可能性是有大小的，能对事件发生的可能性做出描述，能列举出简单实验所有可能发生的结果；
了解必然事件、不可能事件和不确定事件发生的可能性大小，了解事件发生的等可能性的含义，了解概率的意义及概率的取值范围，体会概率是描述不确定事件发生可能性大小的度量，发展随机观念。
能利用概率的意义计算某些事件（古典概型和几何概型）发生的概率，并能设计符合要求的简单数学模型。
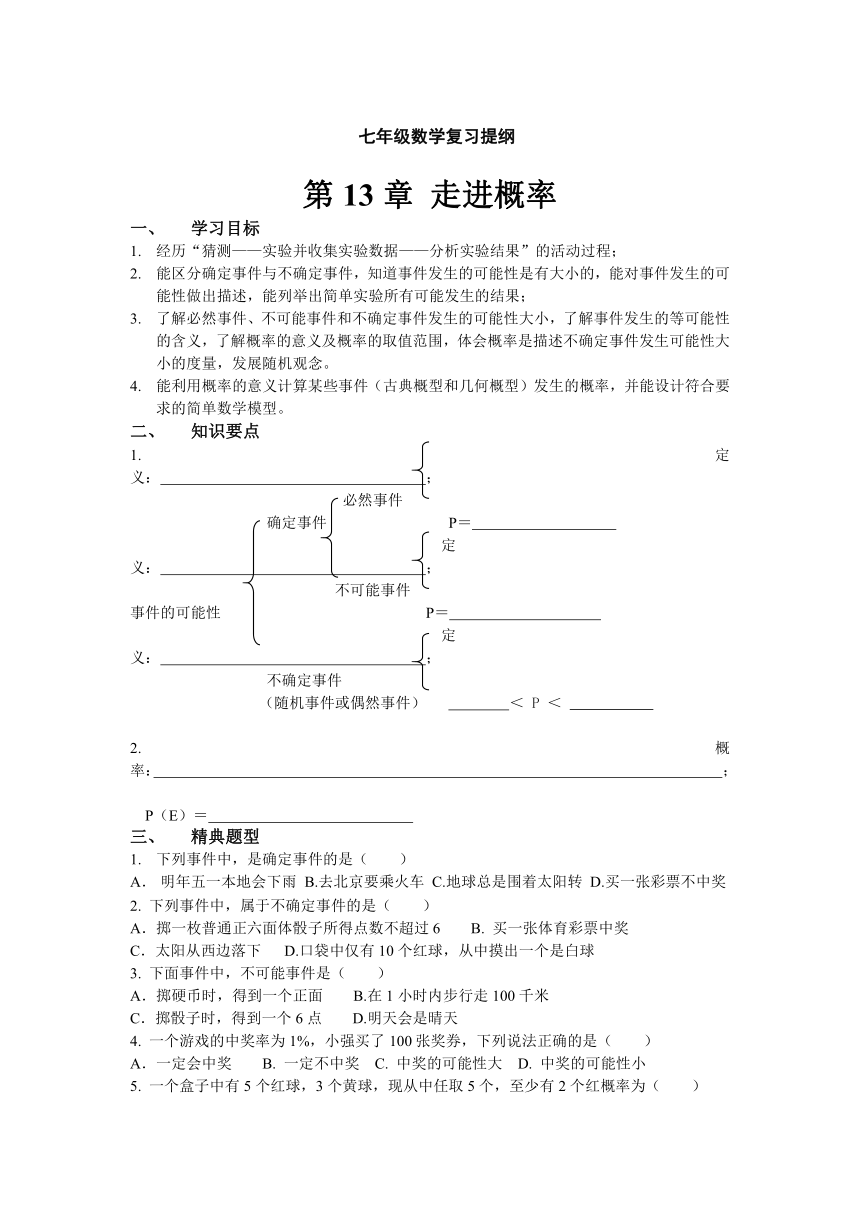
知识要点
1. 定义： ；
必然事件
确定事件 P＝
定义： ；
不可能事件
事件的可能性 P＝
定义： ；
不确定事件
（随机事件或偶然事件） ＜ P ＜
2.概率： ；
P（E）＝
精典题型
下列事件中，是确定事件的是（ ）
明年五一本地会下雨 B.去北京要乘火车 C.地球总是围着太阳转 D.买一张彩票不中奖
2. 下列事件中，属于不确定事件的是（ ）
A．掷一枚普通正六面体骰子所得点数不超过6 B. 买一张体育彩票中奖
C．太阳从西边落下 D.口袋中仅有10个红球，从中摸出一个是白球
3. 下面事件中，不可能事件是（ ）
A．掷硬币时，得到一个正面 B.在1小时内步行走100千米
C．掷骰子时，得到一个6点 D.明天会是晴天
4. 一个游戏的中奖率为1%，小强买了100张奖券，下列说法正确的是（ ）
A．一定会中奖 B. 一定不中奖 C. 中奖的可能性大 D. 中奖的可能性小
5. 一个盒子中有5个红球，3个黄球，现从中任取5个，至少有2个红概率为（ ）
A. B. C. D. 1
6. 从100张已经编号的卡片（从1号到100号），从中任取一张号码是5的倍数的概率是（ ）
A．50% B. 25% C. 20% D. 5%
7. 随机掷一枚均匀的硬币两次，落地后有一次正面朝上的概率是（ ）
A． B. C. D.
8. 在30瓶酸奶中，有3瓶已过了保质期，从中随意抽取一瓶，取得已过保持期酸奶的可能性 ；
9. 盒子里现有5枚白色围棋子，7枚黑色围棋子，则摸不到黑色棋子的概率为 ；
10. 一箱中有24瓶冰红茶饮料，其中有6瓶可以中奖，现从箱中任意摸出一瓶，中奖的概率是 ；
11书包里有数学书3本，英语书2本，语文书5本，从中任意抽取一，则是数学书的概率是 ；
12.小亮和小花用扑克牌做游戏，小花手中有一张牌是“小王”，小亮从小花手中投到“小王”的概率是，则小花手中共有 张牌。
13. 在一个不透明的袋子里装有一些形状、大小完全一样的球（如下表）：
玻 璃 铁 质
红 色 2个 3个
黄 色 4 个 7个
尝试计算下列事件发生的概率：
任意取一个球，是铁质球；
任意取一个球，是红色球；
任意取一个球，是黄色玻璃球；
任意取一个球，是玻璃球；
任意取12个球，恰好红、黄两种颜色的球都有。
14. 两名同学进行射击练习，甲同学射击25次，命中15次；乙同学射击20次，命中2次，谁的命中率高？
15. 妞妞和她的爸爸玩“锤子、剪刀、布”游戏，每次用一只手可以出锤子、剪刀、布三种手势之一，规则是锤子赢剪刀，剪刀赢布，布赢锤子，若两人出相同的手势，则算打平。
（1）请你帮妞妞算算爸爸出“锤子”的概率是多少。
（2）妞妞决定这次出“布”，妞妞赢的概率有多大？
（3）妞妞和爸爸出相同手势的概率是多少？