2020-2021学年人教版数学八年级下册第二十章测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册第二十章测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 21:35:32 | ||
图片预览


文档简介
人教版数学八年级下册第二十章测试卷
姓名:
分数:
一、选择题
1.若1、2、3、x的平均数是6;1、2、3、x、y的平均数是7,则y的值为( )
A.7
B.9
C.11
D.13
2.丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数
3.为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A.方差
B.众数
C.中位数
D.平均数
4.某校一年级学生的平均年龄为7岁,方差为3,5年后该校六年级学生的年龄中( )
A.平均年龄为7岁,方差改变
B.平均年龄为12岁,方差不变C.平均年龄为12岁,方差改变
D.平均年龄不变,方差不变
5.有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的( )
A.平均数
B.中位数
C.众数
D.方差
6.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
A.平均数是9
B.极差是5
C.众数是5
D.中位数是9
7.某市测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
A.50和50
B.50和40
C.40和50
D.40和40
8.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
A.3
B.4
C.5
D.6
9.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
甲
乙
丙
丁
平均数
80
85
85
80
方
差
42
42
54
59
A.甲
B.乙
C.丙
D.丁
二、填空题
10.一组数据2、﹣2、4、1、0的中位数是
.
11.数据1,1,1,3,4的平均数是 ;众数是 .
12.一组数据3,4,0,1,2的平均数与中位数之和是
.
13.某大学生招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是
分.
14.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是
.
三、解答题
15.甲,乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班
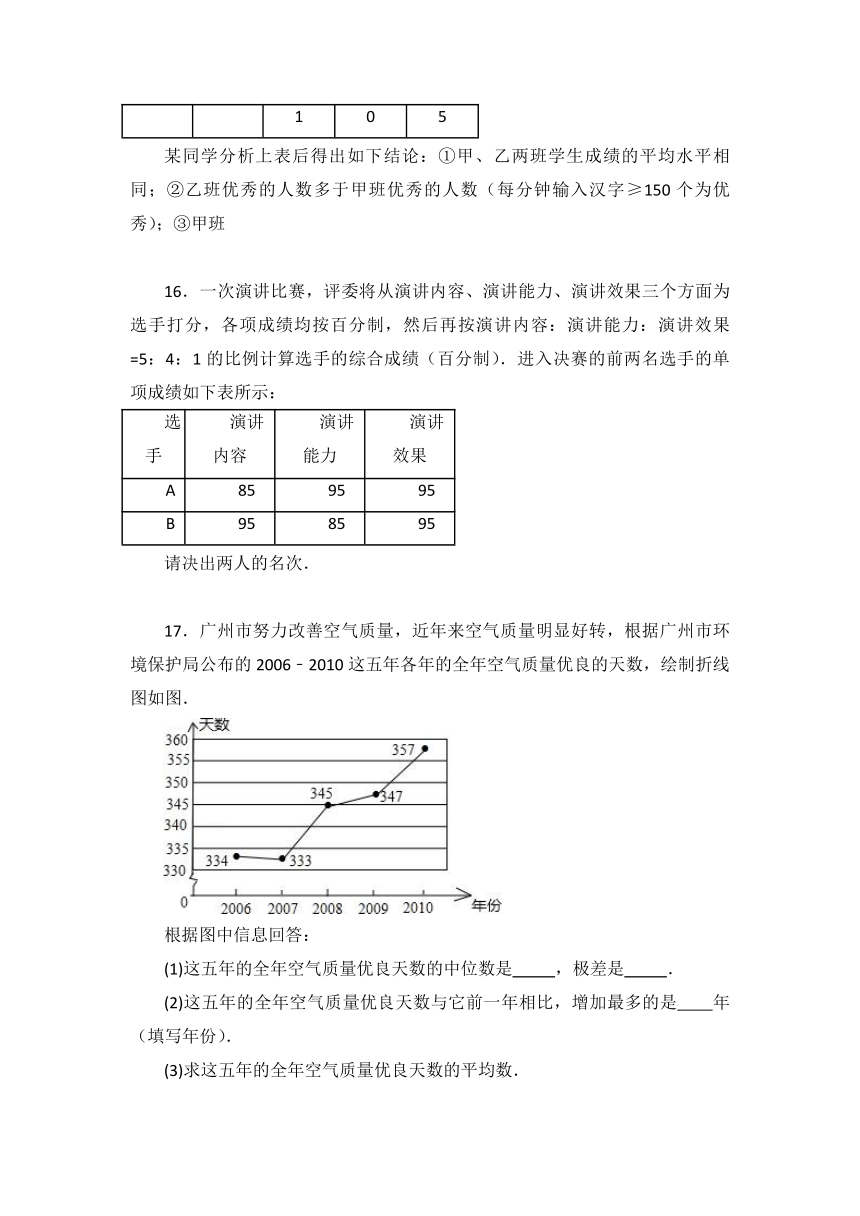
16.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
17.广州市努力改善空气质量,近年来空气质量明显好转,根据广州市环境保护局公布的2006﹣2010这五年各年的全年空气质量优良的天数,绘制折线图如图.
根据图中信息回答:
(1)这五年的全年空气质量优良天数的中位数是
,极差是
.
(2)这五年的全年空气质量优良天数与它前一年相比,增加最多的是 年(填写年份).
(3)求这五年的全年空气质量优良天数的平均数.
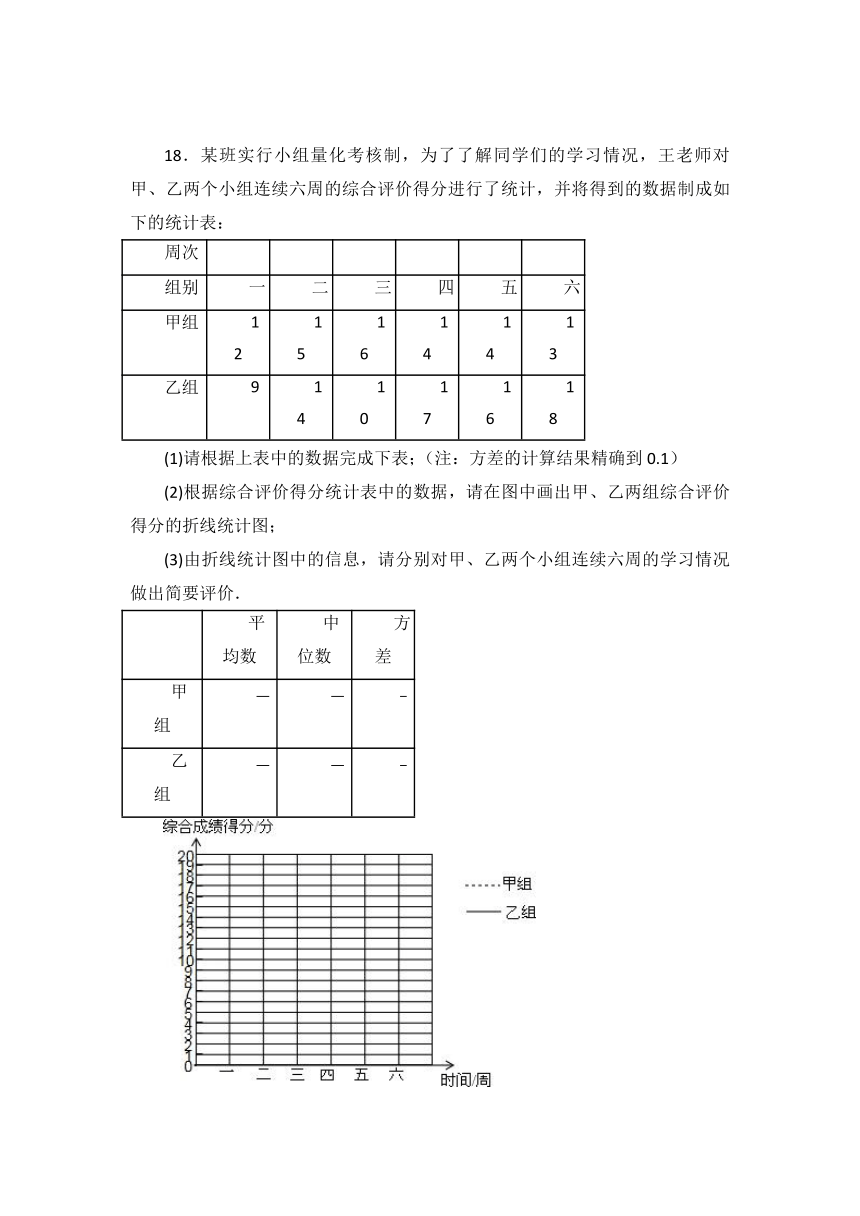
18.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)请根据上表中的数据完成下表;(注:方差的计算结果精确到0.1)
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
平均数
中位数
方差
甲组
乙组
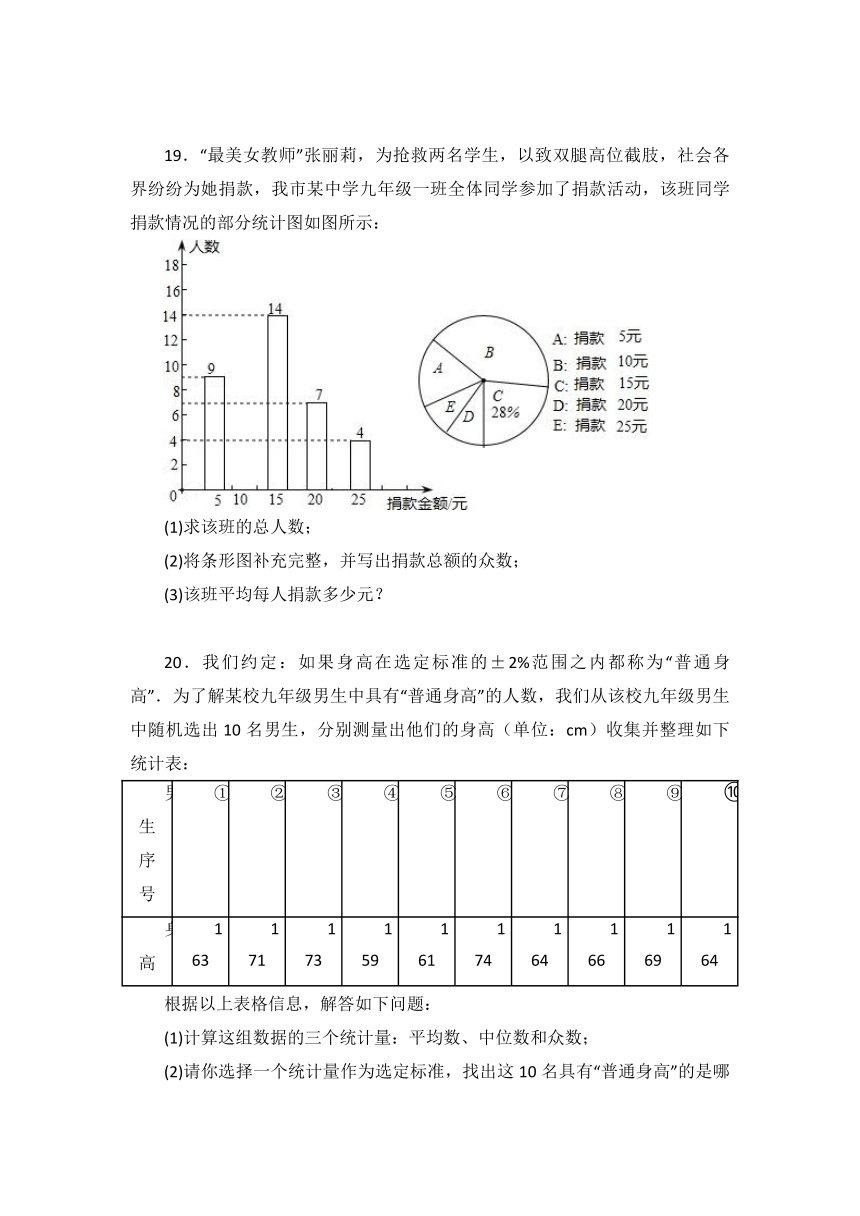
19.“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
20.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理如下统计表:
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择一个统计量作为选定标准,找出这10名具有“普通身高”的是哪几位男生?并说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中“普通身高”的人数约有多少名?
参考答案
1.若1、2、3、x的平均数是6;1、2、3、x、y的平均数是7,则y的值为( )
A.7
B.9
C.11
D.13
【考点】算术平均数.
【专题】选择题.
【分析】根据平均数公式列出方程求得x、y的值.
【解答】解:由题意得:(1+2+3+x)÷4=6①
(1+2+3+x+y)÷5=7②
解①得x=18
把x=18代入②得y=11.
故选C.
【点评】本题考查了平均数的定义.平均数等于所有数据的和除以数据的个数.
2.丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】根据中位数的定义:位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数.
【解答】解:去掉一个最高分和一个最低分对中位数没有影响,
故选D.
【点评】本题考查了统计量的选择,解题的关键是了解中位数的定义,难度不大.
3.为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A.方差
B.众数
C.中位数
D.平均数
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】根据题意,结合员工工资情况,从统计量的角度分析可得答案.
【解答】解:根据题意,了解这家公司的员工的平均工资时,
结合员工情况表,即要全面的了解大多数员工的工资水平,
故最应该关注的数据的中位数,
故选C.
【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
4.某校一年级学生的平均年龄为7岁,方差为3,5年后该校六年级学生的年龄中( )
A.平均年龄为7岁,方差改变
B.平均年龄为12岁,方差不变C.平均年龄为12岁,方差改变
D.平均年龄不变,方差不变
【考点】方差.
【专题】选择题.
【分析】直接利用5年后,平均年龄将增加5,而他们之间岁数差别不变,则方差不变.
【解答】解:∵一年级学生的平均年龄为7岁,方差为3,
∴5年后该校六年级学生的年龄中:平均年龄为12岁,方差不变.
故选B.
【点评】此题主要考查了方差以及平均数,正确把握方差的性质是解题关键.
5.有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的( )
A.平均数
B.中位数
C.众数
D.方差
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】因为第10名同学的成绩排在中间位置,即是中位数.所以需知道这19位同学成绩的中位数.
【解答】解:19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛,中位数就是第10位,因而要判断自己能否进入决赛,他只需知道这19位同学的中位数就可以.
故选B.
【点评】中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.学会运用中位数解决问题.
6.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
A.平均数是9
B.极差是5
C.众数是5
D.中位数是9
【考点】极差;算术平均数;中位数;众数.
【专题】选择题.
【分析】根据极差、平均数、众数、中位数的概念求解.
【解答】解:这组数据的平均数为:=9,
极差为:14﹣5=9,众数为:5,中位数为:9.故选B.
【点评】本题考查了极差、平均数、众数、中位数的知识,掌握各知识点的概念是解答本题的关键.
7.某市测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
A.50和50
B.50和40
C.40和50
D.40和40
【考点】众数;中位数.
【专题】选择题.
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【解答】解:从小到大排列此数据为:37、40、40、50、50、50、75,数据50出现了三次最多,所以50为众数;
50处在第4位是中位数.
故选A.
【点评】本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
8.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
A.3
B.4
C.5
D.6
【考点】算术平均数;众数.
【专题】选择题.
【分析】要求平均数只要求出数据之和再除以总个数即可;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.依此先求出a,再求这组数据的平均数.
【解答】解:数据3,a,4,5的众数为4,即4次数最多;
即a=4.
则其平均数为(3+4+4+5)÷4=4.
故选B.
【点评】本题考查平均数与众数的意义.平均数等于所有数据之和除以数据的总个数;众数是一组数据中出现次数最多的数据.
9.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
甲
乙
丙
丁
平均数
80
85
85
80
方
差
42
42
54
59
A.甲
B.乙
C.丙
D.丁
【考点】方差;算术平均数.
【专题】选择题.
【分析】此题有两个要求:①成绩较好,②状态稳定.于是应选平均数大、方差小的同学参赛.
【解答】解:由于乙的方差较小、平均数较大,故选乙.
故选B.
【点评】本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
10.一组数据2、﹣2、4、1、0的中位数是
.
【考点】中位数.
【专题】填空题.
【分析】按大小顺序排列这组数据,中间两个数的平均数是中位数.
【解答】解:从小到大排列此数据为:﹣2、0、1、2、4,处在中间位置的是1,则1为中位数.
所以本题这组数据的中位数是1.
故答案为1.
【点评】本题属于基础题,考查了确定一组数据的中位数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
11.数据1,1,1,3,4的平均数是 ;众数是 .
【考点】众数;算术平均数.
【专题】填空题.
【分析】利用算术平均数的求法求平均数,众数的定义求众数即可.
【解答】解:平均数为:(1+1+1+3+4)÷5=2;
数据1出现了3次,最多,众数为1.
故答案为2,1.
【点评】本题考查了众数及算术平均数的求法,属于基础题,比较简单.
12.一组数据3,4,0,1,2的平均数与中位数之和是
.
【考点】算术平均数;中位数.
【专题】填空题.
【分析】根据平均数和中位数的概念求出结果,再相加即可.
【解答】解:平均数=(3+4+0+1+2)÷5=2;
数据从小到大排列:0,1,2,3,4,中位数=2;
∴2+2=4.
即平均数与中位数之和是4.故填4.
【点评】考查平均数和中位数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
13.某大学生招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是
分.
【考点】加权平均数.
【专题】填空题.
【分析】按照所给的比例进行计算即可,小明的综合得分=数学成绩×60%+物理成绩×40%.
【解答】解:小明的综合得分=95×60%+90×40%=93(分).
故答案为:93.
【点评】本题考查了加权成绩的计算.加权成绩等于各项成绩乘以不同的权重的和.
14.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是
.
【考点】方差;算术平均数.
【专题】填空题.
【分析】先由平均数公式求得x的值,再由方差公式求解即可.
【解答】解:∵1,3,x,2,5,它的平均数是3,
∴(1+3+x+2+5)÷5=3,
∴x=4,
∴S2=[(1﹣3)2+(3﹣3)2+(4﹣3)2+(2﹣3)2+(5﹣3)2]=2;
∴这个样本的方差是2.
故答案为:2.
【点评】本题考查了平均数和方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
15.甲,乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的是
(把你认为正确结论的序号都填上).
【考点】方差;算术平均数;中位数.
【专题】填空题.
【分析】平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
【解答】解:①由表中可知,平均字数都是135,正确;
②甲班的中位数是149,过半的人数低于150,乙班的中位数是151,过半的人数大于等于151,说明乙的优秀人数多于甲班的,正确;
③甲班的方差大于乙班的,又说明甲班的波动情况大,所以也正确.
故填①②③.
【点评】本题考查了平均数、中位数和方差的意义.对统计中的概念理解是学好统计的关键,这道题把统计初步知识的考查与现代社会生活联系起来,避免了对该部分知识的抽象考查和脱离实际的弊病.
16.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
【考点】加权平均数.
【专题】解答题.
【分析】按照权重为演讲内容:演讲能力:演讲效果=5:4:1的比例计算两人的测试成绩,再进行比较即可求解.
【解答】解:选手A的最后得分是:
(85×5+95×4+95×1)÷(5+4+1)
=900÷10=90,
选手B最后得分是:
(95×5+85×4+95×1)÷(5+4+1)
=910÷10=91.
由上可知选手B获得第一名,选手A获得第二名.
【点评】本题考查的是加权平均数的求法,根据某方面的需要选拔时往往利用加权平均数更合适.
17.广州市努力改善空气质量,近年来空气质量明显好转,根据广州市环境保护局公布的2006﹣2010这五年各年的全年空气质量优良的天数,绘制折线图如图.
根据图中信息回答:
(1)这五年的全年空气质量优良天数的中位数是
,极差是
.
(2)这五年的全年空气质量优良天数与它前一年相比,增加最多的是 年(填写年份).
(3)求这五年的全年空气质量优良天数的平均数.
【考点】折线统计图;算术平均数;中位数;极差.
【专题】解答题.
【分析】(1)把这五年的全年空气质量优良天数按照从小到大排列,根据中位数的定义解答;根据极差的定义,用最大的数减去最小的数即可;
(2)分别求出相邻两年下一年比前一年多的优良天数,然后即可得解;
(3)根据平均数的求解方法列式计算即可得解.
【解答】解:(1)这五年的全年空气质量优良天数按照从小到大排列如下:
333、334、345、347、357,
所以中位数是345;
极差是:357﹣333=24;
(2)2007年与2006年相比,333﹣334=﹣1,
2008年与2007年相比,345﹣333=12,
2009年与2008年相比,347﹣345=2,
2010年与2009年相比,357﹣347=10,
所以增加最多的是2008年;
(3)这五年的全年空气质量优良天数的平均数===343.2天.
【点评】本题考查了折线统计图,要理解极差的概念,中位数的定义,以及算术平均数的求解方法,能够根据计算的数据进行综合分析,熟练掌握对统计图的分析和平均数的计算是解题的关键.
18.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)请根据上表中的数据完成下表;(注:方差的计算结果精确到0.1)
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
平均数
中位数
方差
甲组
乙组
【考点】折线统计图;算术平均数;中位数;方差.
【专题】解答题.
【分析】(1)根据平均数、中位数、方差的定义,可得答案;
(2)根据描点、连线,可得折线统计图;
(3)根据折线统计图中的信息,统计表中的信息,可得答案.
【解答】解:(1)填表如下:
平均数
中位数
方差
甲组
14
14
1.7
乙组
14
15
11.7
(2)如图:
(3)从折线图可看出:甲组成绩相对稳定,但进步不大,且略有下降趋势;乙组成绩不够稳定,但进步较快,呈上升趋势.
【点评】本题考查了折线图的意义和平均数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.
19.“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
【考点】条形统计图;扇形统计图;加权平均数;众数.
【专题】解答题.
【分析】(1)用捐款15元的人数14除以所占的百分比28%,计算即可得解;
(2)用该班总人数减去其它四种捐款额的人数,计算即可求出捐款10元的人数,然后补全条形统计图,根据众数的定义,人数最多即为捐款总额的众数;
(3)根据加权平均数的求解方法列式计算即可得解.
【解答】解:(1)=50(人).
该班总人数为50人;
(2)捐款10元的人数:50﹣9﹣14﹣7﹣4=50﹣34=16,
图形补充如右图所示,众数是10;
(3)(5×9+10×16+15×14+20×7+25×4)=×655=13.1元,
因此,该班平均每人捐款13.1元.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理如下统计表:
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择一个统计量作为选定标准,找出这10名具有“普通身高”的是哪几位男生?并说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中“普通身高”的人数约有多少名?
【考点】众数;用样本估计总体;加权平均数;中位数.
【专题】解答题.
【分析】(1)根据平均数、中位数和众数的定义分别进行计算,即可求出答案;
(2)根据选平均数作为标准,得出身高x满足166.4×(1﹣2%)≤x≤166.4×(1+2%)为“普通身高”,从而得出⑦、⑧、⑨、⑩男生的身高具有“普通身高”;
根据选中位数作为标准,得出身高x满足165×(1﹣2%)≤x≤165×(1+2%),为“普通身高”,从而得出①、⑦、⑧、⑩男生的身高具有“普通身高”;
根据选众数作为标准,得出身高x满足164×(1﹣2%)≤x≤164×(1+2%)为“普通身高”,此时得出①、⑤、⑦、⑧、⑩男生的身高具有“普通身高”.
(3)分三种情况讨论,(1)以平均数作为标准(2)以中位数作为标准(3)以众数数作为标准;分别用总人数乘以所占的百分比,即可得出普通身高的人数.
【解答】解:(1)平均数为:
=166.4(cm),
中位数为:=165(cm),
众数为:164cm;
(2)选平均数作为标准:
身高x满足166.4×(1﹣2%)≤x≤166.4×(1+2%),
即163.072≤x≤169.728时为“普通身高”,
此时⑦、⑧、⑨、⑩男生的身高具有“普通身高”,
选中位数作为标准:
身高x满足165×(1﹣2%)≤x≤165×(1+2%),为“普通身高”,
从而得出①、⑦、⑧、⑩男生的身高具有“普通身高”;
选众数作为标准:
身高x满足164×(1﹣2%)≤x≤164×(1+2%)为“普通身高”,
此时得出①、⑤、⑦、⑧、⑩男生的身高具有“普通身高”.
(3)以平均数作为标准,估计全年级男生中“普通身高”的人数约为:
(人).
【点评】此题考查了中位数、众数、平均数,本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
姓名:
分数:
一、选择题
1.若1、2、3、x的平均数是6;1、2、3、x、y的平均数是7,则y的值为( )
A.7
B.9
C.11
D.13
2.丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数
3.为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A.方差
B.众数
C.中位数
D.平均数
4.某校一年级学生的平均年龄为7岁,方差为3,5年后该校六年级学生的年龄中( )
A.平均年龄为7岁,方差改变
B.平均年龄为12岁,方差不变C.平均年龄为12岁,方差改变
D.平均年龄不变,方差不变
5.有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的( )
A.平均数
B.中位数
C.众数
D.方差
6.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
A.平均数是9
B.极差是5
C.众数是5
D.中位数是9
7.某市测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
A.50和50
B.50和40
C.40和50
D.40和40
8.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
A.3
B.4
C.5
D.6
9.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
甲
乙
丙
丁
平均数
80
85
85
80
方
差
42
42
54
59
A.甲
B.乙
C.丙
D.丁
二、填空题
10.一组数据2、﹣2、4、1、0的中位数是
.
11.数据1,1,1,3,4的平均数是 ;众数是 .
12.一组数据3,4,0,1,2的平均数与中位数之和是
.
13.某大学生招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是
分.
14.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是
.
三、解答题
15.甲,乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班
16.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
17.广州市努力改善空气质量,近年来空气质量明显好转,根据广州市环境保护局公布的2006﹣2010这五年各年的全年空气质量优良的天数,绘制折线图如图.
根据图中信息回答:
(1)这五年的全年空气质量优良天数的中位数是
,极差是
.
(2)这五年的全年空气质量优良天数与它前一年相比,增加最多的是 年(填写年份).
(3)求这五年的全年空气质量优良天数的平均数.
18.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)请根据上表中的数据完成下表;(注:方差的计算结果精确到0.1)
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
平均数
中位数
方差
甲组
乙组
19.“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
20.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理如下统计表:
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择一个统计量作为选定标准,找出这10名具有“普通身高”的是哪几位男生?并说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中“普通身高”的人数约有多少名?
参考答案
1.若1、2、3、x的平均数是6;1、2、3、x、y的平均数是7,则y的值为( )
A.7
B.9
C.11
D.13
【考点】算术平均数.
【专题】选择题.
【分析】根据平均数公式列出方程求得x、y的值.
【解答】解:由题意得:(1+2+3+x)÷4=6①
(1+2+3+x+y)÷5=7②
解①得x=18
把x=18代入②得y=11.
故选C.
【点评】本题考查了平均数的定义.平均数等于所有数据的和除以数据的个数.
2.丽华根据演讲比赛中九位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A.平均数
B.众数
C.方差
D.中位数
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】根据中位数的定义:位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数.
【解答】解:去掉一个最高分和一个最低分对中位数没有影响,
故选D.
【点评】本题考查了统计量的选择,解题的关键是了解中位数的定义,难度不大.
3.为了解某公司员工的年工资情况,小王随机调查了10位员工,其年工资(单位:万元)如下:3,3,3,4,5,5,6,6,8,20,下列统计量中,能合理反映该公司年工资中等水平的是( )
A.方差
B.众数
C.中位数
D.平均数
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】根据题意,结合员工工资情况,从统计量的角度分析可得答案.
【解答】解:根据题意,了解这家公司的员工的平均工资时,
结合员工情况表,即要全面的了解大多数员工的工资水平,
故最应该关注的数据的中位数,
故选C.
【点评】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
4.某校一年级学生的平均年龄为7岁,方差为3,5年后该校六年级学生的年龄中( )
A.平均年龄为7岁,方差改变
B.平均年龄为12岁,方差不变C.平均年龄为12岁,方差改变
D.平均年龄不变,方差不变
【考点】方差.
【专题】选择题.
【分析】直接利用5年后,平均年龄将增加5,而他们之间岁数差别不变,则方差不变.
【解答】解:∵一年级学生的平均年龄为7岁,方差为3,
∴5年后该校六年级学生的年龄中:平均年龄为12岁,方差不变.
故选B.
【点评】此题主要考查了方差以及平均数,正确把握方差的性质是解题关键.
5.有19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛.某同学知道自己的分数后,要判断自己能否进入决赛,他只需知道这19位同学的( )
A.平均数
B.中位数
C.众数
D.方差
【考点】平均数、中位数和众数的比较.
【专题】选择题.
【分析】因为第10名同学的成绩排在中间位置,即是中位数.所以需知道这19位同学成绩的中位数.
【解答】解:19位同学参加歌咏比赛,所得的分数互不相同,取得前10位同学进入决赛,中位数就是第10位,因而要判断自己能否进入决赛,他只需知道这19位同学的中位数就可以.
故选B.
【点评】中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.学会运用中位数解决问题.
6.已知一组数据:12,5,9,5,14,下列说法不正确的是( )
A.平均数是9
B.极差是5
C.众数是5
D.中位数是9
【考点】极差;算术平均数;中位数;众数.
【专题】选择题.
【分析】根据极差、平均数、众数、中位数的概念求解.
【解答】解:这组数据的平均数为:=9,
极差为:14﹣5=9,众数为:5,中位数为:9.故选B.
【点评】本题考查了极差、平均数、众数、中位数的知识,掌握各知识点的概念是解答本题的关键.
7.某市测得一周PM2.5的日均值(单位:)如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是( )
A.50和50
B.50和40
C.40和50
D.40和40
【考点】众数;中位数.
【专题】选择题.
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
【解答】解:从小到大排列此数据为:37、40、40、50、50、50、75,数据50出现了三次最多,所以50为众数;
50处在第4位是中位数.
故选A.
【点评】本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
8.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )
A.3
B.4
C.5
D.6
【考点】算术平均数;众数.
【专题】选择题.
【分析】要求平均数只要求出数据之和再除以总个数即可;众数是一组数据中出现次数最多的数据,注意众数可以不止一个.依此先求出a,再求这组数据的平均数.
【解答】解:数据3,a,4,5的众数为4,即4次数最多;
即a=4.
则其平均数为(3+4+4+5)÷4=4.
故选B.
【点评】本题考查平均数与众数的意义.平均数等于所有数据之和除以数据的总个数;众数是一组数据中出现次数最多的数据.
9.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
甲
乙
丙
丁
平均数
80
85
85
80
方
差
42
42
54
59
A.甲
B.乙
C.丙
D.丁
【考点】方差;算术平均数.
【专题】选择题.
【分析】此题有两个要求:①成绩较好,②状态稳定.于是应选平均数大、方差小的同学参赛.
【解答】解:由于乙的方差较小、平均数较大,故选乙.
故选B.
【点评】本题考查平均数和方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
10.一组数据2、﹣2、4、1、0的中位数是
.
【考点】中位数.
【专题】填空题.
【分析】按大小顺序排列这组数据,中间两个数的平均数是中位数.
【解答】解:从小到大排列此数据为:﹣2、0、1、2、4,处在中间位置的是1,则1为中位数.
所以本题这组数据的中位数是1.
故答案为1.
【点评】本题属于基础题,考查了确定一组数据的中位数的能力.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
11.数据1,1,1,3,4的平均数是 ;众数是 .
【考点】众数;算术平均数.
【专题】填空题.
【分析】利用算术平均数的求法求平均数,众数的定义求众数即可.
【解答】解:平均数为:(1+1+1+3+4)÷5=2;
数据1出现了3次,最多,众数为1.
故答案为2,1.
【点评】本题考查了众数及算术平均数的求法,属于基础题,比较简单.
12.一组数据3,4,0,1,2的平均数与中位数之和是
.
【考点】算术平均数;中位数.
【专题】填空题.
【分析】根据平均数和中位数的概念求出结果,再相加即可.
【解答】解:平均数=(3+4+0+1+2)÷5=2;
数据从小到大排列:0,1,2,3,4,中位数=2;
∴2+2=4.
即平均数与中位数之和是4.故填4.
【点评】考查平均数和中位数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
13.某大学生招生考试只考数学和物理,计算综合得分时,按数学占60%,物理占40%计算,已知小明数学得分为95分,物理得分为90分,那么小明的综合得分是
分.
【考点】加权平均数.
【专题】填空题.
【分析】按照所给的比例进行计算即可,小明的综合得分=数学成绩×60%+物理成绩×40%.
【解答】解:小明的综合得分=95×60%+90×40%=93(分).
故答案为:93.
【点评】本题考查了加权成绩的计算.加权成绩等于各项成绩乘以不同的权重的和.
14.已知一个样本:1,3,5,x,2,它的平均数为3,则这个样本的方差是
.
【考点】方差;算术平均数.
【专题】填空题.
【分析】先由平均数公式求得x的值,再由方差公式求解即可.
【解答】解:∵1,3,x,2,5,它的平均数是3,
∴(1+3+x+2+5)÷5=3,
∴x=4,
∴S2=[(1﹣3)2+(3﹣3)2+(4﹣3)2+(2﹣3)2+(5﹣3)2]=2;
∴这个样本的方差是2.
故答案为:2.
【点评】本题考查了平均数和方差:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
15.甲,乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级
参赛人数
中位数
方差
平均字数
甲
55
149
191
135
乙
55
151
110
135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的是
(把你认为正确结论的序号都填上).
【考点】方差;算术平均数;中位数.
【专题】填空题.
【分析】平均数表示一组数据的平均程度.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
【解答】解:①由表中可知,平均字数都是135,正确;
②甲班的中位数是149,过半的人数低于150,乙班的中位数是151,过半的人数大于等于151,说明乙的优秀人数多于甲班的,正确;
③甲班的方差大于乙班的,又说明甲班的波动情况大,所以也正确.
故填①②③.
【点评】本题考查了平均数、中位数和方差的意义.对统计中的概念理解是学好统计的关键,这道题把统计初步知识的考查与现代社会生活联系起来,避免了对该部分知识的抽象考查和脱离实际的弊病.
16.一次演讲比赛,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容:演讲能力:演讲效果=5:4:1的比例计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
请决出两人的名次.
【考点】加权平均数.
【专题】解答题.
【分析】按照权重为演讲内容:演讲能力:演讲效果=5:4:1的比例计算两人的测试成绩,再进行比较即可求解.
【解答】解:选手A的最后得分是:
(85×5+95×4+95×1)÷(5+4+1)
=900÷10=90,
选手B最后得分是:
(95×5+85×4+95×1)÷(5+4+1)
=910÷10=91.
由上可知选手B获得第一名,选手A获得第二名.
【点评】本题考查的是加权平均数的求法,根据某方面的需要选拔时往往利用加权平均数更合适.
17.广州市努力改善空气质量,近年来空气质量明显好转,根据广州市环境保护局公布的2006﹣2010这五年各年的全年空气质量优良的天数,绘制折线图如图.
根据图中信息回答:
(1)这五年的全年空气质量优良天数的中位数是
,极差是
.
(2)这五年的全年空气质量优良天数与它前一年相比,增加最多的是 年(填写年份).
(3)求这五年的全年空气质量优良天数的平均数.
【考点】折线统计图;算术平均数;中位数;极差.
【专题】解答题.
【分析】(1)把这五年的全年空气质量优良天数按照从小到大排列,根据中位数的定义解答;根据极差的定义,用最大的数减去最小的数即可;
(2)分别求出相邻两年下一年比前一年多的优良天数,然后即可得解;
(3)根据平均数的求解方法列式计算即可得解.
【解答】解:(1)这五年的全年空气质量优良天数按照从小到大排列如下:
333、334、345、347、357,
所以中位数是345;
极差是:357﹣333=24;
(2)2007年与2006年相比,333﹣334=﹣1,
2008年与2007年相比,345﹣333=12,
2009年与2008年相比,347﹣345=2,
2010年与2009年相比,357﹣347=10,
所以增加最多的是2008年;
(3)这五年的全年空气质量优良天数的平均数===343.2天.
【点评】本题考查了折线统计图,要理解极差的概念,中位数的定义,以及算术平均数的求解方法,能够根据计算的数据进行综合分析,熟练掌握对统计图的分析和平均数的计算是解题的关键.
18.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次
组别
一
二
三
四
五
六
甲组
12
15
16
14
14
13
乙组
9
14
10
17
16
18
(1)请根据上表中的数据完成下表;(注:方差的计算结果精确到0.1)
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图;
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况做出简要评价.
平均数
中位数
方差
甲组
乙组
【考点】折线统计图;算术平均数;中位数;方差.
【专题】解答题.
【分析】(1)根据平均数、中位数、方差的定义,可得答案;
(2)根据描点、连线,可得折线统计图;
(3)根据折线统计图中的信息,统计表中的信息,可得答案.
【解答】解:(1)填表如下:
平均数
中位数
方差
甲组
14
14
1.7
乙组
14
15
11.7
(2)如图:
(3)从折线图可看出:甲组成绩相对稳定,但进步不大,且略有下降趋势;乙组成绩不够稳定,但进步较快,呈上升趋势.
【点评】本题考查了折线图的意义和平均数的概念.平均数是指在一组数据中所有数据之和再除以数据的个数.平均数是表示一组数据集中趋势的量数,它是反映数据集中趋势的一项指标.解答平均数应用题的关键在于确定“总数量”以及和总数量对应的总份数.
19.“最美女教师”张丽莉,为抢救两名学生,以致双腿高位截肢,社会各界纷纷为她捐款,我市某中学九年级一班全体同学参加了捐款活动,该班同学捐款情况的部分统计图如图所示:
(1)求该班的总人数;
(2)将条形图补充完整,并写出捐款总额的众数;
(3)该班平均每人捐款多少元?
【考点】条形统计图;扇形统计图;加权平均数;众数.
【专题】解答题.
【分析】(1)用捐款15元的人数14除以所占的百分比28%,计算即可得解;
(2)用该班总人数减去其它四种捐款额的人数,计算即可求出捐款10元的人数,然后补全条形统计图,根据众数的定义,人数最多即为捐款总额的众数;
(3)根据加权平均数的求解方法列式计算即可得解.
【解答】解:(1)=50(人).
该班总人数为50人;
(2)捐款10元的人数:50﹣9﹣14﹣7﹣4=50﹣34=16,
图形补充如右图所示,众数是10;
(3)(5×9+10×16+15×14+20×7+25×4)=×655=13.1元,
因此,该班平均每人捐款13.1元.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.我们约定:如果身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理如下统计表:
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数和众数;
(2)请你选择一个统计量作为选定标准,找出这10名具有“普通身高”的是哪几位男生?并说明理由;
(3)若该年级共有280名男生,按(2)中选定标准,请你估算出该年级男生中“普通身高”的人数约有多少名?
【考点】众数;用样本估计总体;加权平均数;中位数.
【专题】解答题.
【分析】(1)根据平均数、中位数和众数的定义分别进行计算,即可求出答案;
(2)根据选平均数作为标准,得出身高x满足166.4×(1﹣2%)≤x≤166.4×(1+2%)为“普通身高”,从而得出⑦、⑧、⑨、⑩男生的身高具有“普通身高”;
根据选中位数作为标准,得出身高x满足165×(1﹣2%)≤x≤165×(1+2%),为“普通身高”,从而得出①、⑦、⑧、⑩男生的身高具有“普通身高”;
根据选众数作为标准,得出身高x满足164×(1﹣2%)≤x≤164×(1+2%)为“普通身高”,此时得出①、⑤、⑦、⑧、⑩男生的身高具有“普通身高”.
(3)分三种情况讨论,(1)以平均数作为标准(2)以中位数作为标准(3)以众数数作为标准;分别用总人数乘以所占的百分比,即可得出普通身高的人数.
【解答】解:(1)平均数为:
=166.4(cm),
中位数为:=165(cm),
众数为:164cm;
(2)选平均数作为标准:
身高x满足166.4×(1﹣2%)≤x≤166.4×(1+2%),
即163.072≤x≤169.728时为“普通身高”,
此时⑦、⑧、⑨、⑩男生的身高具有“普通身高”,
选中位数作为标准:
身高x满足165×(1﹣2%)≤x≤165×(1+2%),为“普通身高”,
从而得出①、⑦、⑧、⑩男生的身高具有“普通身高”;
选众数作为标准:
身高x满足164×(1﹣2%)≤x≤164×(1+2%)为“普通身高”,
此时得出①、⑤、⑦、⑧、⑩男生的身高具有“普通身高”.
(3)以平均数作为标准,估计全年级男生中“普通身高”的人数约为:
(人).
【点评】此题考查了中位数、众数、平均数,本题属于基础题,考查了确定一组数据的中位数和众数的能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
