18.1.1平行四边形的性质(2) 课件(共23张PPT)
文档属性
| 名称 | 18.1.1平行四边形的性质(2) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 21:12:40 | ||
图片预览





文档简介
第十八章 平行四边形
18.1.1平行四边形的性质(2)
2021年春人教版八年级(下)数学
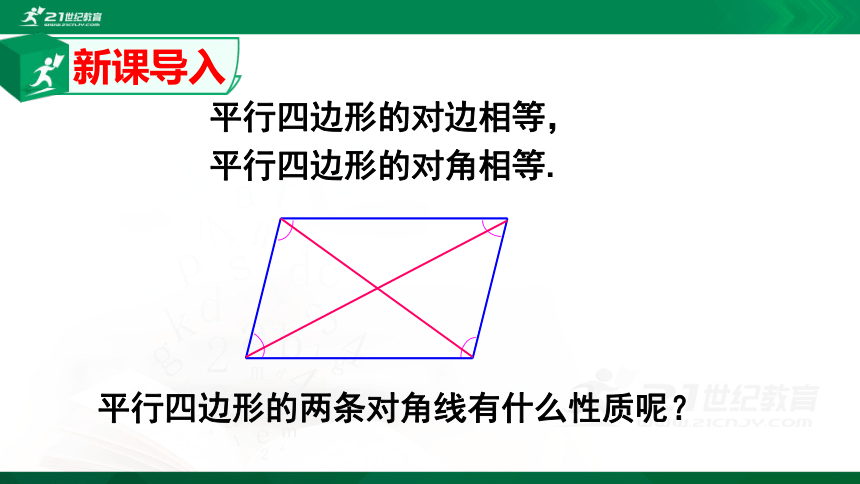
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的两条对角线有什么性质呢?
新课导入
1. 知道平行四边形的对角线互相平分的性质.
2.能运用这一性质进行推理与计算.
性质的探究.(重点)
性质的灵活运用.(难点)
学习目标
一,平行四边形的两条对角线关系
探究
如图,在 ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
A
B
C
D
O
探究新知
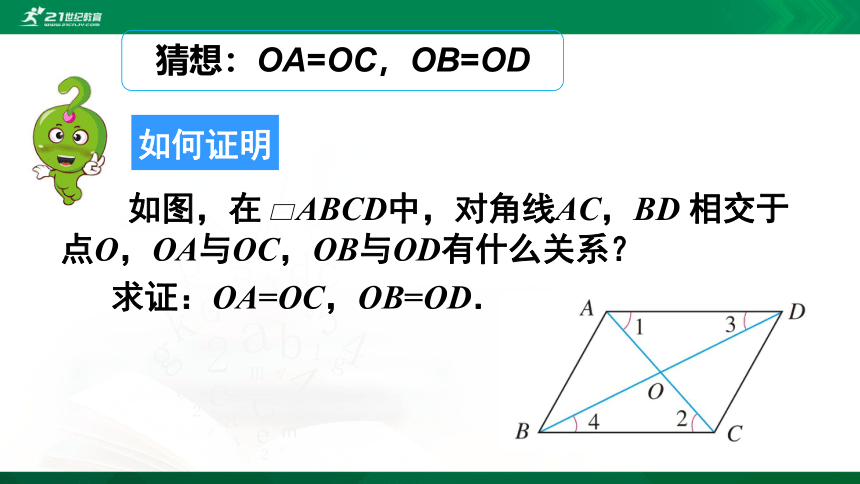
猜想:OA=OC,OB=OD
如何证明
如图,在 ABCD中,对角线AC,BD 相交于点O,OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
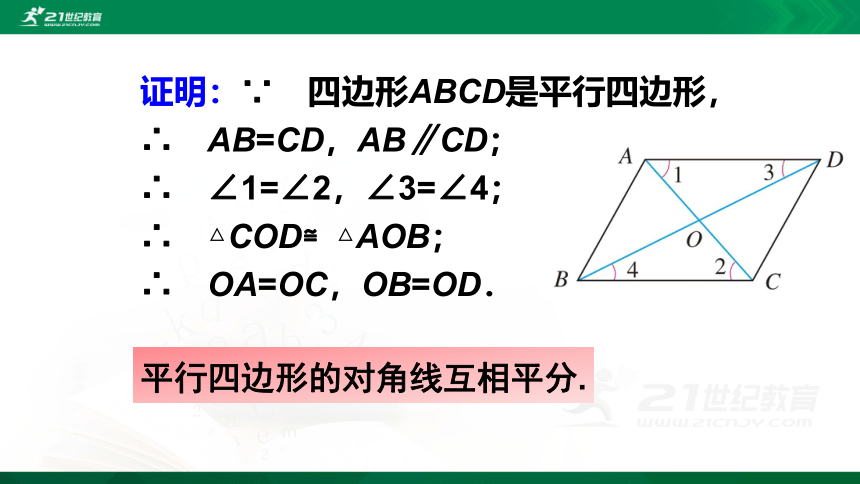
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
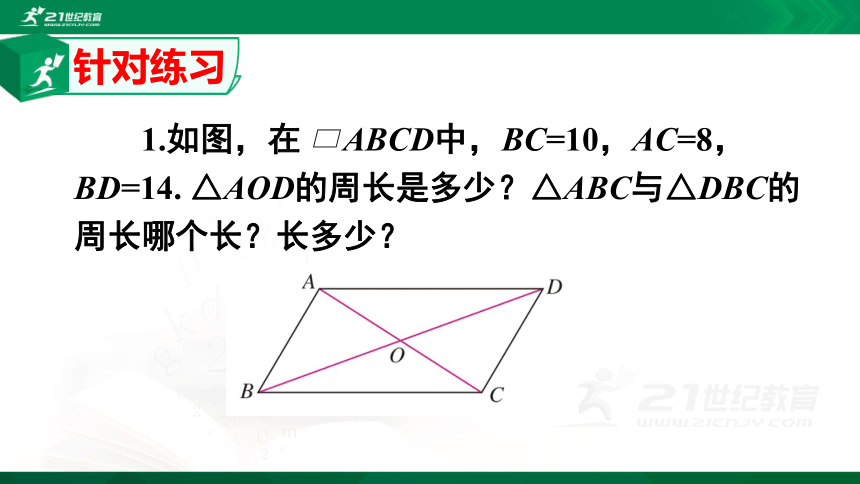
1.如图,在 ABCD中,BC=10,AC=8,BD=14. △AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
针对练习
解:∵四边形ABCD是平行四边形
∴AD=BC=10
OA=OC=4
OD=OB=7
∴ l△AOD= AD+OA+OD=10+4+7=21
∵ AB=CD BC=BC
BD – AC=14 – 8=6
∴△DBC的周长较长,长6.
2. ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC长为( )
A、5cm B、15cm
C、6cm D、16cm
A
二,平行四边形的性质应用
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥BC. 求BC,CD,AC,OA的长,以及
ABCD的面积
探究新知
解: ∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC.
∴△ABC是直角三角形.
根据勾股定理,
又OA=OC,∴
1.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.
求证:OE=OF.
针对练习
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC (平行四边形的性质)
∴∠EAO=∠FCO(两直线平行,内错角相等)
在△AOE和△COF中
∠AOE = ∠ COF﹙对顶角相等﹚
OA = OC
∠EAO = ∠FCO
∴ △AOE≌△COF (ASA )
∴ OE = OF (全等三角形的对应边相等)
2.平行四边形的两条对角线把它分成的四个三角形( )
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
我们证明了平行四边形具有以下性质:(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
归纳小结
1. ABCD中,AC、BD相交于O, ABCD的周长为20cm,△AOB的周长比△BOC的周长小4cm,则AB=_____,BC=_____.
3cm
7cm
课堂练习
2. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
33
3.一个平行四边形的一边长为8,一条对角线长为6,则另一条对角线x的取值范围为:_____________
10<x<22.
4.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
证明:由平行四边形的性质 得:OB=OD. ∵AB∥CD,
∴∠EBO=∠FDO.
又∵∠EOB=∠FOD,
∴△EOB≌△FOD.
∴OE=OF.
5.如图,在 ABCD中,对角线AC、BD相交于O,AC=6,BD=8,AB=5,
(1)求 ABCD的周长;
(2)求 ABCD的面积.
解:(1)由平行四边形的性质得:
OC=OA=????????AC=3,OB=OD=????????BD=4.
在△AOB中,OA2+OB2=32+42=52=AB2.
?
∴△AOB是直角三角形,∠AOB=90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
A
B
C
D
O
在 ABCD中,
AO=CO,BO=DO.
课堂小结
谢谢聆听
18.1.1平行四边形的性质(2)
2021年春人教版八年级(下)数学
平行四边形的对边相等,
平行四边形的对角相等.
平行四边形的两条对角线有什么性质呢?
新课导入
1. 知道平行四边形的对角线互相平分的性质.
2.能运用这一性质进行推理与计算.
性质的探究.(重点)
性质的灵活运用.(难点)
学习目标
一,平行四边形的两条对角线关系
探究
如图,在 ABCD中,连接AC,BD,并设它们相交于点O,OA与OC,OB与OD有什么关系?你能证明发现的结论吗?
A
B
C
D
O
探究新知
猜想:OA=OC,OB=OD
如何证明
如图,在 ABCD中,对角线AC,BD 相交于点O,OA与OC,OB与OD有什么关系?
求证:OA=OC,OB=OD.
证明:∵ 四边形ABCD是平行四边形,
∴ AB=CD,AB∥CD;
∴ ∠1=∠2,∠3=∠4;
∴ △COD≌△AOB;
∴ OA=OC,OB=OD.
平行四边形的对角线互相平分.
1.如图,在 ABCD中,BC=10,AC=8,BD=14. △AOD的周长是多少?△ABC与△DBC的周长哪个长?长多少?
针对练习
解:∵四边形ABCD是平行四边形
∴AD=BC=10
OA=OC=4
OD=OB=7
∴ l△AOD= AD+OA+OD=10+4+7=21
∵ AB=CD BC=BC
BD – AC=14 – 8=6
∴△DBC的周长较长,长6.
2. ABCD的周长为40cm,△ABC的周长为25cm,则对角线AC长为( )
A、5cm B、15cm
C、6cm D、16cm
A
二,平行四边形的性质应用
例2 如图,在 ABCD中,AB=10,AD=8,AC⊥BC. 求BC,CD,AC,OA的长,以及
ABCD的面积
探究新知
解: ∵四边形ABCD是平行四边形,
∴BC=AD=8,CD=AB=10.
∵AC⊥BC.
∴△ABC是直角三角形.
根据勾股定理,
又OA=OC,∴
1.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.
求证:OE=OF.
针对练习
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC (平行四边形的性质)
∴∠EAO=∠FCO(两直线平行,内错角相等)
在△AOE和△COF中
∠AOE = ∠ COF﹙对顶角相等﹚
OA = OC
∠EAO = ∠FCO
∴ △AOE≌△COF (ASA )
∴ OE = OF (全等三角形的对应边相等)
2.平行四边形的两条对角线把它分成的四个三角形( )
A、都是等腰三角形
B、都是全等三角形
C、都是直角三角形
D、是面积相等的三角形
D
我们证明了平行四边形具有以下性质:(1)平行四边形的对边相等;
(2)平行四边形的对角相等;
(3)平行四边形的对角线互相平分.
归纳小结
1. ABCD中,AC、BD相交于O, ABCD的周长为20cm,△AOB的周长比△BOC的周长小4cm,则AB=_____,BC=_____.
3cm
7cm
课堂练习
2. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
33
3.一个平行四边形的一边长为8,一条对角线长为6,则另一条对角线x的取值范围为:_____________
10<x<22.
4.如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
证明:由平行四边形的性质 得:OB=OD. ∵AB∥CD,
∴∠EBO=∠FDO.
又∵∠EOB=∠FOD,
∴△EOB≌△FOD.
∴OE=OF.
5.如图,在 ABCD中,对角线AC、BD相交于O,AC=6,BD=8,AB=5,
(1)求 ABCD的周长;
(2)求 ABCD的面积.
解:(1)由平行四边形的性质得:
OC=OA=????????AC=3,OB=OD=????????BD=4.
在△AOB中,OA2+OB2=32+42=52=AB2.
?
∴△AOB是直角三角形,∠AOB=90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
A
B
C
D
O
在 ABCD中,
AO=CO,BO=DO.
课堂小结
谢谢聆听
