福建省泉州南安国光中学2019-2020学年度下期九年级数学第一次网测数学试题(word版含答案)
文档属性
| 名称 | 福建省泉州南安国光中学2019-2020学年度下期九年级数学第一次网测数学试题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 21:22:54 | ||
图片预览



文档简介
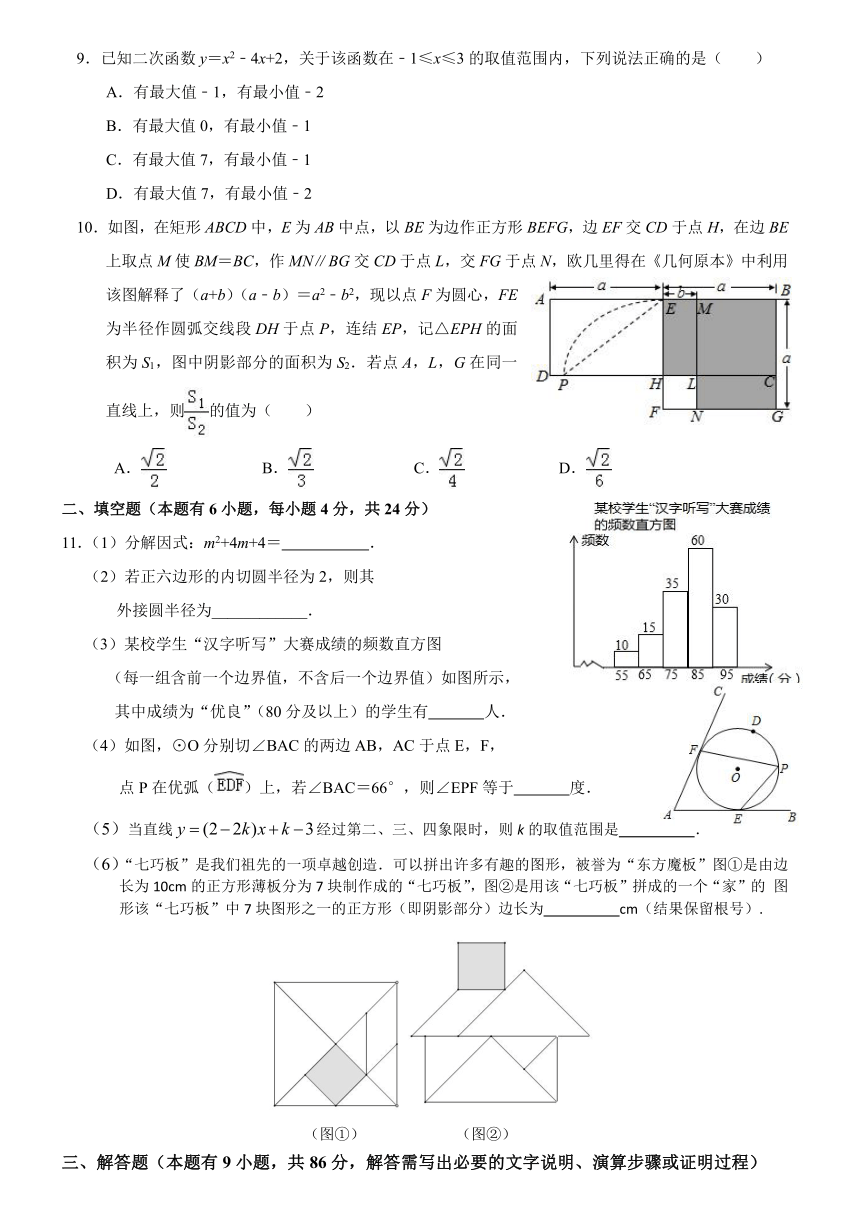
国光中学2020年春季防疫期网络考试
初三数学科试卷
(试卷满分:150分;考试时间:120分钟)
班级 座号 姓名 成绩
一、选择题(本题有10小题,每小题4分,共40分)
1.计算:(﹣3)×5的结果是( )
A.﹣15 B.15 C.﹣2 D.2
2.太阳距离银河系中心约为250 000 000 000 000 000公里,其中数据
250 000 000 000 000 000用科学记数法表示为( )
A.0.25×1018 B.2.5×1017 C.25×1016 D.2.5×1016
3.某露天舞台如图所示,它的俯视图是( )
4.在同一副扑克牌中抽取2张“方块”,3张”梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )
A. B. C. D.
5.对某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),
绘制成如图所示统计图.已知选择鲳鱼的有40人,那么选择黄鱼
的有( )
A.20人 B.40人 C.60人 D.80人
6.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A.y= B.y= C.y= D.y=
7.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A. B.2π C.3π D.6π
8.某简易房示意图如图所示,它是一个轴对称图形,
则屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
9.已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值﹣1,有最小值﹣2
B.有最大值0,有最小值﹣1
C.有最大值7,有最小值﹣1
D.有最大值7,有最小值﹣2
10.如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N,欧几里得在《几何原本》中利用该图解释了(a+b)(a﹣b)=a2﹣b2,现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则的值为( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.(1)分解因式:m2+4m+4= .
(2)若正六边形的内切圆半径为2,则其
外接圆半径为____________.
(3)某校学生“汉字听写”大赛成绩的频数直方图
(每一组含前一个边界值,不含后一个边界值)如图所示,
其中成绩为“优良”(80分及以上)的学生有 人.
(4)如图,⊙O分别切∠BAC的两边AB,AC于点E,F,
点P在优弧()上,若∠BAC=66°,则∠EPF等于 度.
(5)当直线经过第二、三、四象限时,则k的取值范围是 .
(6)“七巧板”是我们祖先的一项卓越创造.可以拼出许多有趣的图形,被誉为“东方魔板”图①是由边长为10cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的 图形该“七巧板”中7块图形之一的正方形(即阴影部分)边长为 cm(结果保留根号).
(图①) (图②)
三、解答题(本题有9小题,共86分,解答需写出必要的文字说明、演算步骤或证明过程)
12.(24分)(1)计算: |﹣6|﹣+(1﹣)0﹣(﹣3).
(2)解方程
(3)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作
CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF.
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
13.(16分)(1)车间有20名工人,某一天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) 9 10 11 12 13 15 16 19 20
工人人数(人) 1 1 6 4 2 2 2 1 1
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
(2)如图,AD是△ABC的角平分线.
(1)作线段AD的垂直平分线EF,分别交AB、AC于点E、F;
(2)(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)
连接DE、DF,四边形AEDF是_________形.(直接写出答案)
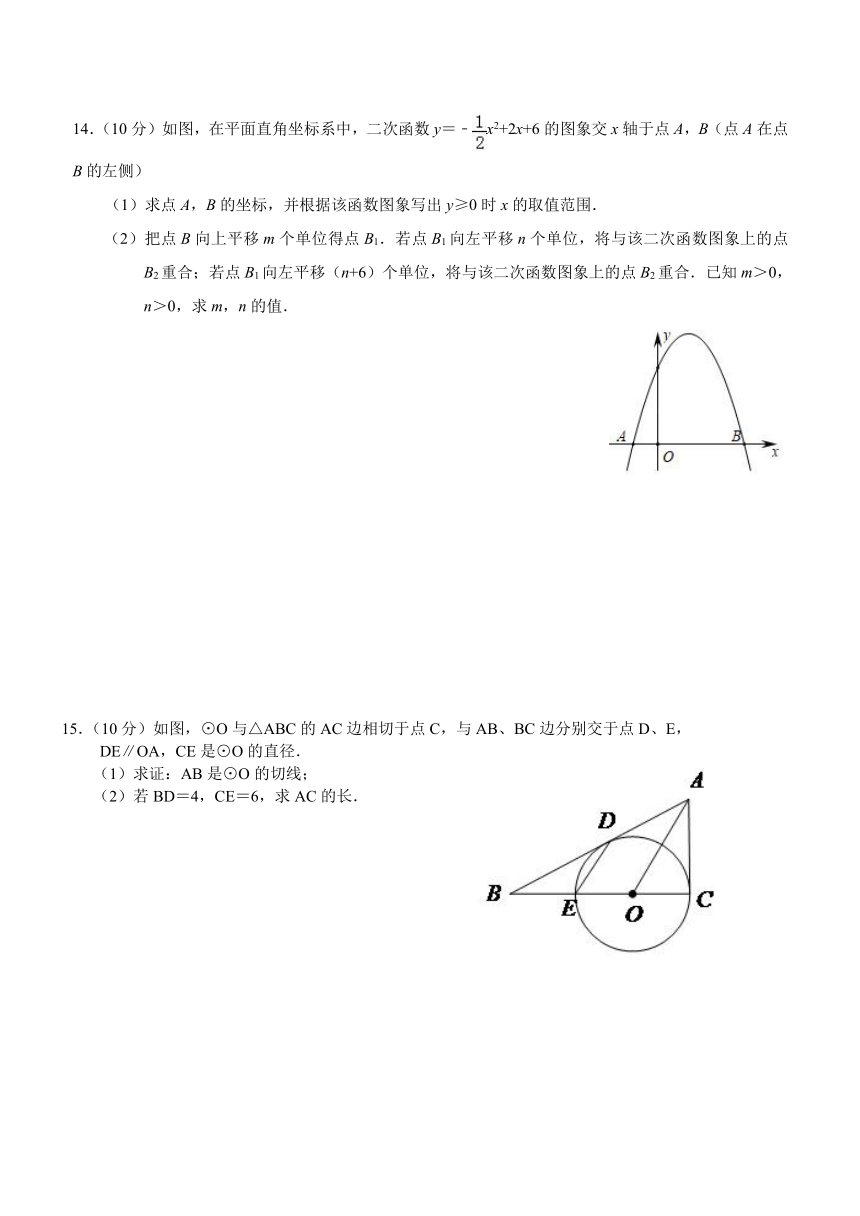
14.(10分)如图,在平面直角坐标系中,二次函数y=﹣x2+2x+6的图象交x轴于点A,B(点A在点B的左侧)
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围.
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B2重合.已知m>0,n>0,求m,n的值.
15.(10分)如图,⊙O与△ABC的AC边相切于点C,与AB、BC边分别交于点D、E,
DE∥OA,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若BD=4,CE=6,求AC的长.
16.(12分)某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
17.(14分)如图,在平面直角坐标系中,直线y=﹣x+4分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某一点Q1向终点Q2匀速运动,它们同时到达终点.
(1)求点B的坐标和OE的长
(2)设点Q2为(m,n),当=tan∠EOF时,求点Q2的坐标.
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点,当点Q在线段上时,设=s,AP=t,求s关于t 的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
答案
1~10 A. B.B.A. D.A.C.B.D.C.
11. (m+2)2 .
12.
13 90.
14. 57°
15. 1<k<3
16.
17.解:(1)原式=6﹣3+1+3
=7;
18.去分母:2x-5+3(x-2)=3x-3,
去括号:2x-5+3x-6=3x-3,
移项,合并:2x=8,
系数化为1:x=4,
经检验,x=4是原分式方程的解.
19.(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,
∴BD=CD,
∴△BDE≌△CDF(AAS);
(2)解:∵△BDE≌△CDF,
∴BE=CF=2,
∴AB=AE+BE=1+2=3,
∵AD⊥BC,BD=CD,
∴AC=AB=3.
20.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)中位数为=12(个),众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
21.(8分)
(1)如图所示:直线EF就是线段AD的垂直平分线.
(2)菱形.
22.(10分)解:(1)令y=0,则﹣,
解得,x1=﹣2,x2=6,
∴A(﹣2,0),B(6,0),
由函数图象得,当y≥0时,﹣2≤x≤6;
(2)由题意得,B1(6﹣n,m),B2(﹣n,m),
函数图象的对称轴为直线,
∵点B1,B2在二次函数图象上且纵坐标相同,
∴,
∴n=1,
∴,
∴m,n的值分别为,1.
23.(10分)证明:(1)连接OD,
∵DE∥OA,
∴∠AOC=∠OED,∠AOD=∠ODE,
∵OD=OE,∴∠OED=∠ODE,
∴∠AOC=∠AOD,
又∵OA=OA,OD=OC,
∴△AOC≌△AOD(SAS),
∴∠ADO=∠ACO.
∵CE是⊙O的直径,AC为⊙O的切线,
∴OC⊥AC,
∴∠ OCA=90°,
∴∠ADO==90°,
∴OD⊥AB,
∵OD为⊙O的半径,
∴AB是⊙O的切线.
(2)∵CE=6,
∴OD=OC=3,
∵∠BDO=90°,
∴,
∵BD=4,
∴OB==5,
∴BC=8,
∵∠BDO=∠ OCA=90°,∠B=∠B,
∴△BDO∽△BCA,
∴,
∴,
∴AC=6.
24.解:(1)设成人有x人,少年y人,
,
解得,,
答:该旅行团中成人与少年分别是17人、5人;
(2)①由题意可得,
由成人8人和少年5人带队,则所需门票的总费用是:100×8+5×100×0.8+(10﹣8)×100×0.6=1320(元),
答:由成人8人和少年5人带队,则所需门票的总费用是1320元;
②设可以安排成人a人,少年b人带队,则1≤a≤17,1≤b≤5,
当10≤a≤17时,
若a=10,则费用为100×10+100×b×0.8≤1200,得b≤2.5,
∴b的最大值是2,此时a+b=12,费用为1160元;
若a=11,则费用为100×11+100×b×0.8≤1200,得b≤,
∴b的最大值是1,此时a+b=12,费用为1180元;
若a≥12,100a≥1200,即成人门票至少是1200元,不合题意,舍去;
当1≤a<10时,
若a=9,则费用为100×9+100b×0.8+100×1×0.6≤1200,得b≤3,
∴b的最大值是3,a+b=12,费用为1200元;
若a=8,则费用为100×8+100b×0.8+100×2×0.6≤1200,得b≤3.5,
∴b的最大值是3,a+b=11<12,不合题意,舍去;
同理,当a<8时,a+b<12,不合题意,舍去;
综上所述,最多安排成人和少年12人带队,有三个方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中成人10人,少年2人时购票费用最少.
25.(14分)解:(1)令y=0,则﹣x+4=0,
∴x=8,
∴B(8,0),
∵C(0,4),
∴OC=4,OB=8,
在Rt△BOC中,BC==4;
(2)如图1,作EM⊥OC于M,则EM∥CD,
∵E是BC的中点
∴M是OC的中点
∴EM=OB=4,OE=BC=2
∵∠CDN=∠NEM,∠CND=∠MNE
∴△CDN∽△MEN,
∴=1,
∴CN=MN=1,
∴EN==,
∵S△ONE=EN?OF=ON?EM,
∴OF==,
由勾股定理得:EF===,
∴tan∠EOF===,
∴==,
∵n=﹣m+4,
∴m=6,n=1,
∴Q2(6,1);
(3)①∵动点P、Q同时作匀速直线运动,
∴s关于t成一次函数关系,设s=kt+b,
∵当点P运动到AO中点时,点Q恰好与点C重合,
∴t=2时,CD=4,DQ3=2,
∴s=Q3C==2,
∵Q3(﹣4,6),Q2(6,1),
∴t=4时,s==5,
将或代入得,解得:,
∴s=﹣,
②(i)当PQ∥OE时,如图2,∠QPB=∠EOB=∠OBE,
作QH⊥x轴于点H,则PH=BH=PB,
Rt△ABQ3中,AQ3=6,AB=4+8=12,
∴BQ3==6,
∵BQ=6﹣s=6﹣t+=7﹣t,
∵cos∠QBH====,
∴BH=14﹣3t,
∴PB=28﹣6t,
∴t+28﹣6t=12,t=;
(ii)当PQ∥OF时,如图3,过点Q作QG⊥AQ3于点G,过点P作PH⊥GQ于点H,
由△Q3QG∽△CBO得:Q3G:QG:Q3Q=1:2:,
∵Q3Q=s=t﹣,
∴Q3G=t﹣1,GQ=3t﹣2,
∴PH=AG=AQ3﹣Q3G=6﹣(t﹣1)=7﹣t,
∴QH=QG﹣AP=3t﹣2﹣t=2t﹣2,
∵∠HPQ=∠CDN,
∴tan∠HPQ=tan∠CDN=,
∴2t﹣2=,t=,
(iii)由图形可知PQ不可能与EF平行,
综上,当PQ与△OEF的一边平行时,AP的长为或.
初三数学科试卷
(试卷满分:150分;考试时间:120分钟)
班级 座号 姓名 成绩
一、选择题(本题有10小题,每小题4分,共40分)
1.计算:(﹣3)×5的结果是( )
A.﹣15 B.15 C.﹣2 D.2
2.太阳距离银河系中心约为250 000 000 000 000 000公里,其中数据
250 000 000 000 000 000用科学记数法表示为( )
A.0.25×1018 B.2.5×1017 C.25×1016 D.2.5×1016
3.某露天舞台如图所示,它的俯视图是( )
4.在同一副扑克牌中抽取2张“方块”,3张”梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( )
A. B. C. D.
5.对某社区居民最爱吃的鱼类进行问卷调查后(每人选一种),
绘制成如图所示统计图.已知选择鲳鱼的有40人,那么选择黄鱼
的有( )
A.20人 B.40人 C.60人 D.80人
6.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A.y= B.y= C.y= D.y=
7.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A. B.2π C.3π D.6π
8.某简易房示意图如图所示,它是一个轴对称图形,
则屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
9.已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( )
A.有最大值﹣1,有最小值﹣2
B.有最大值0,有最小值﹣1
C.有最大值7,有最小值﹣1
D.有最大值7,有最小值﹣2
10.如图,在矩形ABCD中,E为AB中点,以BE为边作正方形BEFG,边EF交CD于点H,在边BE上取点M使BM=BC,作MN∥BG交CD于点L,交FG于点N,欧几里得在《几何原本》中利用该图解释了(a+b)(a﹣b)=a2﹣b2,现以点F为圆心,FE为半径作圆弧交线段DH于点P,连结EP,记△EPH的面积为S1,图中阴影部分的面积为S2.若点A,L,G在同一直线上,则的值为( )
A. B. C. D.
二、填空题(本题有6小题,每小题4分,共24分)
11.(1)分解因式:m2+4m+4= .
(2)若正六边形的内切圆半径为2,则其
外接圆半径为____________.
(3)某校学生“汉字听写”大赛成绩的频数直方图
(每一组含前一个边界值,不含后一个边界值)如图所示,
其中成绩为“优良”(80分及以上)的学生有 人.
(4)如图,⊙O分别切∠BAC的两边AB,AC于点E,F,
点P在优弧()上,若∠BAC=66°,则∠EPF等于 度.
(5)当直线经过第二、三、四象限时,则k的取值范围是 .
(6)“七巧板”是我们祖先的一项卓越创造.可以拼出许多有趣的图形,被誉为“东方魔板”图①是由边长为10cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的 图形该“七巧板”中7块图形之一的正方形(即阴影部分)边长为 cm(结果保留根号).
(图①) (图②)
三、解答题(本题有9小题,共86分,解答需写出必要的文字说明、演算步骤或证明过程)
12.(24分)(1)计算: |﹣6|﹣+(1﹣)0﹣(﹣3).
(2)解方程
(3)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作
CF∥AB交ED的延长线于点F.
(1)求证:△BDE≌△CDF.
(2)当AD⊥BC,AE=1,CF=2时,求AC的长.
13.(16分)(1)车间有20名工人,某一天他们生产的零件个数统计如下表.
车间20名工人某一天生产的零件个数统计表
生产零件的个数(个) 9 10 11 12 13 15 16 19 20
工人人数(人) 1 1 6 4 2 2 2 1 1
(1)求这一天20名工人生产零件的平均个数.
(2)为了提高大多数工人的积极性,管理者准备实行“每天定额生产,超产有奖”的措施.如果你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
(2)如图,AD是△ABC的角平分线.
(1)作线段AD的垂直平分线EF,分别交AB、AC于点E、F;
(2)(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)
连接DE、DF,四边形AEDF是_________形.(直接写出答案)
14.(10分)如图,在平面直角坐标系中,二次函数y=﹣x2+2x+6的图象交x轴于点A,B(点A在点B的左侧)
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围.
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B2重合.已知m>0,n>0,求m,n的值.
15.(10分)如图,⊙O与△ABC的AC边相切于点C,与AB、BC边分别交于点D、E,
DE∥OA,CE是⊙O的直径.
(1)求证:AB是⊙O的切线;
(2)若BD=4,CE=6,求AC的长.
16.(12分)某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
17.(14分)如图,在平面直角坐标系中,直线y=﹣x+4分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某一点Q1向终点Q2匀速运动,它们同时到达终点.
(1)求点B的坐标和OE的长
(2)设点Q2为(m,n),当=tan∠EOF时,求点Q2的坐标.
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点,当点Q在线段上时,设=s,AP=t,求s关于t 的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
答案
1~10 A. B.B.A. D.A.C.B.D.C.
11. (m+2)2 .
12.
13 90.
14. 57°
15. 1<k<3
16.
17.解:(1)原式=6﹣3+1+3
=7;
18.去分母:2x-5+3(x-2)=3x-3,
去括号:2x-5+3x-6=3x-3,
移项,合并:2x=8,
系数化为1:x=4,
经检验,x=4是原分式方程的解.
19.(1)证明:∵CF∥AB,
∴∠B=∠FCD,∠BED=∠F,
∵AD是BC边上的中线,
∴BD=CD,
∴△BDE≌△CDF(AAS);
(2)解:∵△BDE≌△CDF,
∴BE=CF=2,
∴AB=AE+BE=1+2=3,
∵AD⊥BC,BD=CD,
∴AC=AB=3.
20.解:(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个);
答:这一天20名工人生产零件的平均个数为13个;
(2)中位数为=12(个),众数为11个,
当定额为13个时,有8人达标,6人获奖,不利于提高工人的积极性;
当定额为12个时,有12人达标,6人获奖,不利于提高大多数工人的积极性;
当定额为11个时,有18人达标,12人获奖,有利于提高大多数工人的积极性;
∴定额为11个时,有利于提高大多数工人的积极性.
21.(8分)
(1)如图所示:直线EF就是线段AD的垂直平分线.
(2)菱形.
22.(10分)解:(1)令y=0,则﹣,
解得,x1=﹣2,x2=6,
∴A(﹣2,0),B(6,0),
由函数图象得,当y≥0时,﹣2≤x≤6;
(2)由题意得,B1(6﹣n,m),B2(﹣n,m),
函数图象的对称轴为直线,
∵点B1,B2在二次函数图象上且纵坐标相同,
∴,
∴n=1,
∴,
∴m,n的值分别为,1.
23.(10分)证明:(1)连接OD,
∵DE∥OA,
∴∠AOC=∠OED,∠AOD=∠ODE,
∵OD=OE,∴∠OED=∠ODE,
∴∠AOC=∠AOD,
又∵OA=OA,OD=OC,
∴△AOC≌△AOD(SAS),
∴∠ADO=∠ACO.
∵CE是⊙O的直径,AC为⊙O的切线,
∴OC⊥AC,
∴∠ OCA=90°,
∴∠ADO==90°,
∴OD⊥AB,
∵OD为⊙O的半径,
∴AB是⊙O的切线.
(2)∵CE=6,
∴OD=OC=3,
∵∠BDO=90°,
∴,
∵BD=4,
∴OB==5,
∴BC=8,
∵∠BDO=∠ OCA=90°,∠B=∠B,
∴△BDO∽△BCA,
∴,
∴,
∴AC=6.
24.解:(1)设成人有x人,少年y人,
,
解得,,
答:该旅行团中成人与少年分别是17人、5人;
(2)①由题意可得,
由成人8人和少年5人带队,则所需门票的总费用是:100×8+5×100×0.8+(10﹣8)×100×0.6=1320(元),
答:由成人8人和少年5人带队,则所需门票的总费用是1320元;
②设可以安排成人a人,少年b人带队,则1≤a≤17,1≤b≤5,
当10≤a≤17时,
若a=10,则费用为100×10+100×b×0.8≤1200,得b≤2.5,
∴b的最大值是2,此时a+b=12,费用为1160元;
若a=11,则费用为100×11+100×b×0.8≤1200,得b≤,
∴b的最大值是1,此时a+b=12,费用为1180元;
若a≥12,100a≥1200,即成人门票至少是1200元,不合题意,舍去;
当1≤a<10时,
若a=9,则费用为100×9+100b×0.8+100×1×0.6≤1200,得b≤3,
∴b的最大值是3,a+b=12,费用为1200元;
若a=8,则费用为100×8+100b×0.8+100×2×0.6≤1200,得b≤3.5,
∴b的最大值是3,a+b=11<12,不合题意,舍去;
同理,当a<8时,a+b<12,不合题意,舍去;
综上所述,最多安排成人和少年12人带队,有三个方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中成人10人,少年2人时购票费用最少.
25.(14分)解:(1)令y=0,则﹣x+4=0,
∴x=8,
∴B(8,0),
∵C(0,4),
∴OC=4,OB=8,
在Rt△BOC中,BC==4;
(2)如图1,作EM⊥OC于M,则EM∥CD,
∵E是BC的中点
∴M是OC的中点
∴EM=OB=4,OE=BC=2
∵∠CDN=∠NEM,∠CND=∠MNE
∴△CDN∽△MEN,
∴=1,
∴CN=MN=1,
∴EN==,
∵S△ONE=EN?OF=ON?EM,
∴OF==,
由勾股定理得:EF===,
∴tan∠EOF===,
∴==,
∵n=﹣m+4,
∴m=6,n=1,
∴Q2(6,1);
(3)①∵动点P、Q同时作匀速直线运动,
∴s关于t成一次函数关系,设s=kt+b,
∵当点P运动到AO中点时,点Q恰好与点C重合,
∴t=2时,CD=4,DQ3=2,
∴s=Q3C==2,
∵Q3(﹣4,6),Q2(6,1),
∴t=4时,s==5,
将或代入得,解得:,
∴s=﹣,
②(i)当PQ∥OE时,如图2,∠QPB=∠EOB=∠OBE,
作QH⊥x轴于点H,则PH=BH=PB,
Rt△ABQ3中,AQ3=6,AB=4+8=12,
∴BQ3==6,
∵BQ=6﹣s=6﹣t+=7﹣t,
∵cos∠QBH====,
∴BH=14﹣3t,
∴PB=28﹣6t,
∴t+28﹣6t=12,t=;
(ii)当PQ∥OF时,如图3,过点Q作QG⊥AQ3于点G,过点P作PH⊥GQ于点H,
由△Q3QG∽△CBO得:Q3G:QG:Q3Q=1:2:,
∵Q3Q=s=t﹣,
∴Q3G=t﹣1,GQ=3t﹣2,
∴PH=AG=AQ3﹣Q3G=6﹣(t﹣1)=7﹣t,
∴QH=QG﹣AP=3t﹣2﹣t=2t﹣2,
∵∠HPQ=∠CDN,
∴tan∠HPQ=tan∠CDN=,
∴2t﹣2=,t=,
(iii)由图形可知PQ不可能与EF平行,
综上,当PQ与△OEF的一边平行时,AP的长为或.
同课章节目录
