黑龙江省哈尔滨工业大学附属中学2019——2020学年六年级下学期月考数学试卷(4月份)(五四学制) (word版含解析)
文档属性
| 名称 | 黑龙江省哈尔滨工业大学附属中学2019——2020学年六年级下学期月考数学试卷(4月份)(五四学制) (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-07 00:00:00 | ||
图片预览



文档简介
2019-2020学年黑龙江省哈尔滨工大附中六年级(下)月考数学试卷(4月份)(五四学制)
一.选择题(每题3分,共30分)
1.下列各对数中,数值相等的是( )
A.﹣27与(﹣2)7 B.﹣32与(﹣3)2
C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)3
2.x﹣y的相反数是( )
A.x+y B.﹣x﹣y C.y﹣x D.x﹣y
3.下列计算正确的是( )
A.4a﹣9a=5a B.a﹣a=a
C.a3﹣a2=a D.a+a=a2
4.如图,从上面看如图的几何体得到的平面图形是( )
A. B. C. D.
5.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
6.下面调查统计中,适合做全面调查的是( )
A.雪花牌电冰箱的市场占有率
B.蓓蕾专栏电视节目的收视率
C.飞马牌汽车每百公里的耗油量
D.今天班主任张老师与几名同学谈话
7.为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )
A.抽取的50名男生是总体
B.50名男生是样本容量
C.每一名男生的体重是个体
D.这种调查是全面调查
8.若a为有理数,则下列说法正确的是( )
A.﹣(a﹣2)2是负数 B.|a2+3|是正数
C.﹣1+(1﹣a)4是负数 D.以上说法都不对
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
10.下列说法不正确有( )个
(1)一个数的平方一定大于这个数;
(2)是有理数;
(3)一个数的平方一定小于这个数的绝对值;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是±1或0.
A.1 B.2 C.3 D.4
二.填空题:(每小题3分,共30分)
11.地球上的海洋面积约为36100000千米2,用科学记数法表示为 千米2.
12.的值是 .
13.若a2=4,|b|=3且a>b,则a﹣b= .
14.若x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,则正整数n的值为 .
15.已知关于x,y的多项式﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7不含二次项,则m+n= .
16.已知一个样本有100个数据,这组数据的最大值为36,最小值为12,如果组距取4,则把数据分成 组.
17.若定义一种新运算,规定=ad﹣bc,则= .
18.如果2x2﹣3x的值为﹣1,则6x﹣4x2+3的值为 .
19.火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x、y、z的箱子按如图所示的方式打包,则打包带的长至少为 .
20.在数轴上A、B两点分别表示的数是2和8,在数轴上,点A右侧有另外一点P到A、B的距离和是10,则点P表示的数是 .
三、解答题
21.计算:
(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2;
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×].
22.先化简,再求值:5ab﹣2[3ab﹣(4ab2+ab)]﹣5ab2,其中a=,b=﹣.
23.某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如图的两幅统计图:
(1)该调查小组共抽取了 名学生;
(2)样本学生中阳光体育运动时间为1.5小时的人数是 ,并补全频数分布直方图;
(3)请通过计算估计该市中小学生一天中阳光体育运动的平均时间.
24.如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为300米,宽为100米,圆形花坛的半径为20米,求广场空地的面积(π取3.14).
25.在长江某段笔直的航道上依次有三个城市A、O、B,长江水流的方向为自西向东,水流的速度为每小时m千米,以O为原点建立数轴,取向东的方向为正方向,选取1千米为一个单位长度,A、B两城市所对应的数分别为a、b,满足|a+200|+(a+b)2=0.
(1)求A、B两个城市所对应的数;
(2)有两艘轮船P、Q分别从A、B两个城市同时出发相向而行,两船在静水中的速度分别为每小时40千米和每小时60千米,求P、Q两船相遇地点C所对应的数;
(3)在(2)的条件下,当m=10时,P、Q两船继续按原速原方向行驶,当Q到达A城市后,立即返回,两船都向东继续行驶,从相遇时刻起经过多长时间P、Q两船相距200千米?并直接写出此时P船在数轴上所对应的数.
2019-2020学年黑龙江省哈尔滨工大附中六年级(下)月考数学试卷(4月份)(五四学制)
参考答案与试题解析
一.选择题(每题3分,共30分)
1.下列各对数中,数值相等的是( )
A.﹣27与(﹣2)7 B.﹣32与(﹣3)2
C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)3
【分析】根据有理数乘方的法则对个选项的值进行逐一判断,找出数值相同的项.
【解答】解:A、根据有理数乘方的法则可知,(﹣2)7=﹣27,故A选项符合题意;
B、﹣32=﹣9,(﹣3)2=9,故B选项不符合题意;
C、﹣3×23=﹣24,﹣32×2=﹣18,故C选项不符合题意;
D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,故D选项不符合题意.
故选:A.
2.x﹣y的相反数是( )
A.x+y B.﹣x﹣y C.y﹣x D.x﹣y
【分析】根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:将x﹣y括起来,前面加一个“﹣”号,即可得到x﹣y的相反数﹣(x﹣y)=y﹣x.
故选:C.
3.下列计算正确的是( )
A.4a﹣9a=5a B.a﹣a=a
C.a3﹣a2=a D.a+a=a2
【分析】根据合并同类项的法则把系数相加即可.
【解答】解:A、系数相加字母及指数不变,故A不符合题意;
B、系数相加字母及指数不变,故B符合题意;
C、不是同类项不能合并,故C不符合题意;
D、系数相加字母及指数不变,故D不符合题意;
故选:B.
4.如图,从上面看如图的几何体得到的平面图形是( )
A. B. C. D.
【分析】从上面看得到从左往右2列,正方形的个数依次为2,1,依此画出图形即可.
【解答】解:根据几何体可得此图形的俯视图从左往右有2列,正方形的个数依次为2,1.
故选:A.
5.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
【分析】根据由几个单项式的和组成的式子叫多项式解答即可.
【解答】解:在式子,2πx2y,,y2﹣5,π+6,中,
多项式有:,y2﹣5,共2个.
故选:B.
6.下面调查统计中,适合做全面调查的是( )
A.雪花牌电冰箱的市场占有率
B.蓓蕾专栏电视节目的收视率
C.飞马牌汽车每百公里的耗油量
D.今天班主任张老师与几名同学谈话
【分析】适合普查的方式一般有以下几种:
①范围较小;②容易掌控;③不具有破坏性;
④可操作性较强.
【解答】解:A、B、C中,容量太大,不易做全面调查,故选D.
7.为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )
A.抽取的50名男生是总体
B.50名男生是样本容量
C.每一名男生的体重是个体
D.这种调查是全面调查
【分析】根据总体的定义判断A,总体:所要考察对象的全体;
根据样本容量的定义判断B,个体:每一个考察对象;
根据个体的定义判断C,样本:从总体中抽取的部分考察对象称为样本;
根据普查的定义判断D,普查就是都查一遍,比如全国人口普查,就是把中国所有的人都点一遍.抽查就是抽取其中的一部分来检查统计,适用于破坏性或者工作量大的统计调查工作.
【解答】解:A、级498名男生的体重是全体,故本选项不合题意;
B、50是样本容量,故本选项不合题意;
C、每一名男生的体重是个体,故本选项符合题意;
D、从七年级498名学生中抽取50名学生进行测量,这种调查是抽样调查,故本选项符合题意.
故选:C.
8.若a为有理数,则下列说法正确的是( )
A.﹣(a﹣2)2是负数 B.|a2+3|是正数
C.﹣1+(1﹣a)4是负数 D.以上说法都不对
【分析】利用偶次幂和绝对值都具有非负性解答即可.
【解答】解:A、﹣(a﹣2)2是负数,说法错误,例如a=2时,﹣(a﹣2)2是零,不是负数;
B、|a2+3|是正数,说法正确;
C、﹣1+(1﹣a)4是负数,说法错误,例如a=1,﹣1+(1﹣a)4是零;
D、以上说法都不对,说法错误;
故选:B.
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:因圆柱的展开面为长方形,AC展开应该是两直线,且有公共点C.
故选:B.
10.下列说法不正确有( )个
(1)一个数的平方一定大于这个数;
(2)是有理数;
(3)一个数的平方一定小于这个数的绝对值;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是±1或0.
A.1 B.2 C.3 D.4
【分析】根据有理数的乘方、有理数和绝对值的性质分别对每一项进行分析,即可得出答案.
【解答】解:(1)一个数的平方为正数与0,不一定都大于这个数;
(2)是有理数;
(3)一个数的平方不一定小于这个数的绝对值,例如,(﹣1)2=|﹣1|;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是1或0;
其中不正确有3个;
故选:C.
二.填空题:(每小题3分,共30分)
11.地球上的海洋面积约为36100000千米2,用科学记数法表示为 3.61×107 千米2.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将36100000用科学记数法表示为:3.61×107.
故答案为:3.61×107.
12.的值是 .
【分析】积的乘方,等于每个因式乘方的积,据此计算即可.
【解答】解:
=
=
=
=
=
=.
故答案为:.
13.若a2=4,|b|=3且a>b,则a﹣b= 1或5 .
【分析】先根据已知条件确定a、b的值,再计算a﹣b.
【解答】解:∵a2=4,|b|=3,
∴a=±2,b=±3.
由a>b,可得a=2,b=±3.
当a=2,b=﹣3时,a﹣b=2+3=5;
当a=﹣2,b=﹣3时,a﹣b=﹣2﹣(﹣3)=1.
故答案为:1或5.
14.若x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,则正整数n的值为 2或1 .
【分析】根据多项式的次数定义和n是正整数得出4+n=6或4+n=5,求出n的值即可.
【解答】解:∵x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,
又∵n是正整数,
∴4+n=6或4+n=5,
∴n=2或n=1;
故答案为:2或1.
15.已知关于x,y的多项式﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7不含二次项,则m+n= ﹣1.5 .
【分析】先合并同类项,然后根据多项式不含二次项可知5m=0,2n+3=0,从而可求得m、n的值,然后代入计算即可.
【解答】解:﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7=﹣5x2y﹣(2n+3)xy+5my2+4x﹣7,
∵多项式不含二次项,
∴5m=0,2n+3=0,
解得m=0,n=﹣1.5,
∴m+n=﹣1.5,
故答案为:﹣1.5.
16.已知一个样本有100个数据,这组数据的最大值为36,最小值为12,如果组距取4,则把数据分成 6 组.
【分析】根据题意和题目中的数据,可以计算出要分成几组.
【解答】解:36﹣12=24,
24÷4=6,
即这些数据要分成6组,
故答案为:6.
17.若定义一种新运算,规定=ad﹣bc,则= ﹣43 .
【分析】根据=ad﹣bc,用5与﹣2的积减去﹣3与﹣11的积,求出的值是多少即可.
【解答】解:∵=ad﹣bc,
∴
=5×(﹣2)﹣(﹣3)×(﹣11)
=﹣10﹣33
=﹣43.
故答案为:﹣43.
18.如果2x2﹣3x的值为﹣1,则6x﹣4x2+3的值为 5 .
【分析】首先把6x﹣4x2+3化成﹣2(2x2﹣3x)+3,然后把2x2﹣3x=﹣1代入化简后的算式求解即可.
【解答】解:∵2x2﹣3x=﹣1,
∴6x﹣4x2+3
=﹣2(2x2﹣3x)+3
=﹣2×(﹣1)+3
=2+3
=5.
故答案为:5.
19.火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x、y、z的箱子按如图所示的方式打包,则打包带的长至少为 4y+6z+2x .
【分析】本题实际上就是求长方体的侧面的周长.
【解答】解:根据题意,得
2×(y+z)×2+2×(z+x)=4y+6z+2x.
故答案为:4y+6z+2x.
20.在数轴上A、B两点分别表示的数是2和8,在数轴上,点A右侧有另外一点P到A、B的距离和是10,则点P表示的数是 10 .
【分析】根据数轴上两点距离的计算方法,列方程求解即可.
【解答】解:∵数轴上A、B两点分别表示的数是2和8,
∴AB=|8﹣2|=6,
又∵点A右侧有另外一点P到A、B的距离和是10,
∴点P在点B的右侧,
设点P所表示的数为x,
则(x﹣2)+(x﹣8)=10,
解得x=10,
故答案为:10.
三、解答题
21.计算:
(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2;
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×].
【分析】(1)首先计算乘方,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先计算乘方和中括号里面的运算,然后计算中括号外面的乘法,求出算式的值是多少即可.
【解答】解:(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2
=×××
=.
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×]
=﹣3×[25×(﹣)+60×]
=﹣3×(﹣15+15)
=﹣3×0
=0.
22.先化简,再求值:5ab﹣2[3ab﹣(4ab2+ab)]﹣5ab2,其中a=,b=﹣.
【分析】原式去括号合并得到最简结果,将a与b的值代入计算即可求出值.
【解答】解:原式=5ab﹣6ab+8ab2+ab﹣5ab2=3ab2,
当a=,b=﹣时,原式=.
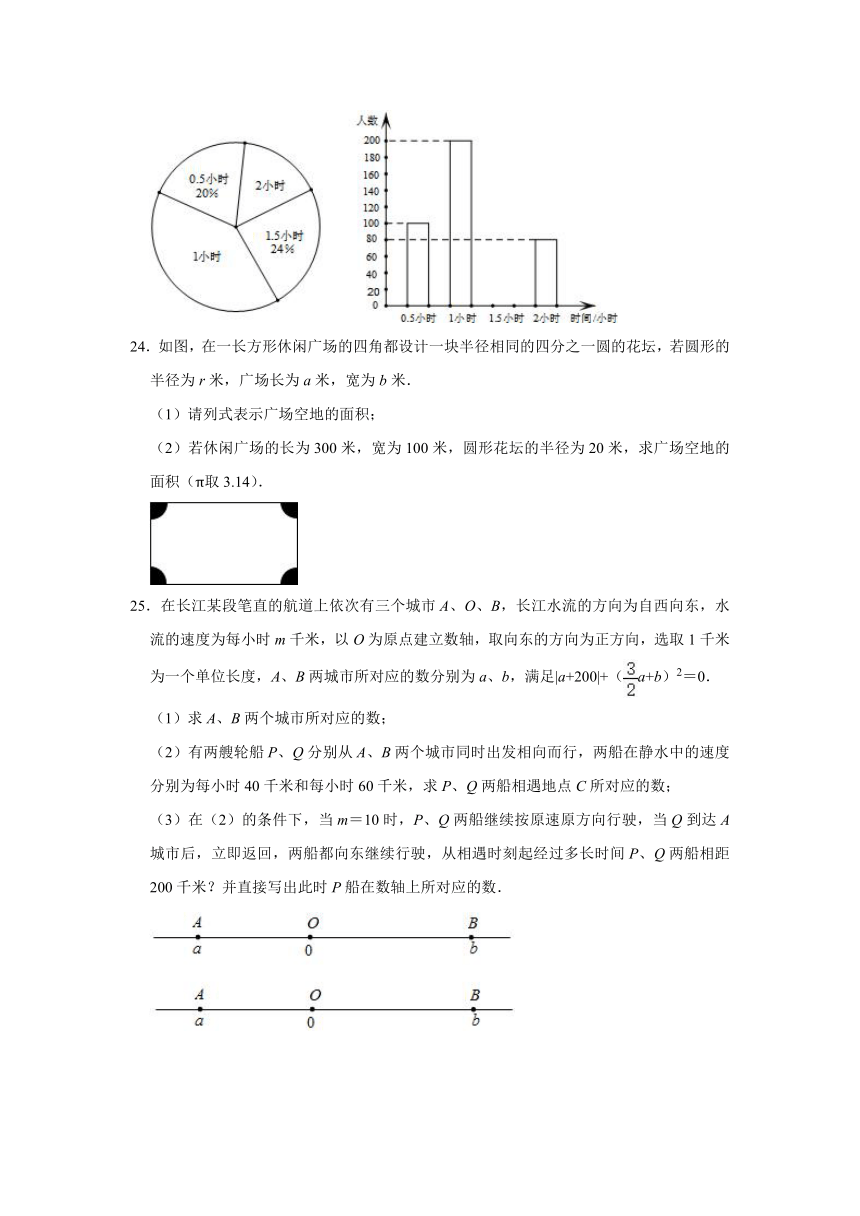
23.某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如图的两幅统计图:
(1)该调查小组共抽取了 500 名学生;
(2)样本学生中阳光体育运动时间为1.5小时的人数是 120 ,并补全频数分布直方图;
(3)请通过计算估计该市中小学生一天中阳光体育运动的平均时间.
【分析】(1)利用0.5小时的人数为:100人,所占比例为:20%,即可求出样本容量;
(2)利用样本容量乘以1.5小时的百分数,即可求出1.5小时的人数,画图即可;
(3)计算出该市中小学生一天中阳光体育运动的平均时间即可.
【解答】解:(1)由题意可得:0.5小时的人数为:100人,所占比例为:20%,
100÷20%=500,
∴本次调查共抽样了500名学生;
故答案为500;
(2)1.5小时的人数为:500×24%=120(人)
故答案为120,
如图所示:
(3)根据题意得:=1.18,即该市中小学生一天中阳光体育运动的平均时间约1小时.
24.如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为300米,宽为100米,圆形花坛的半径为20米,求广场空地的面积(π取3.14).
【分析】(1)根据广场空地的面积等于长方形的面积减去四个四分之一圆形的花坛的面积即可得;
(2)根据题(1)的结论,将相应的数代入计算即可得.
【解答】解:(1)矩形的面积为ab,
四分之一圆形的花坛的面积为πr2,
则广场空地的面积为ab﹣4×πr2=ab﹣πr2,
答:广场空地的面积为(ab﹣πr2)米2;
(2)由题意得:a=300米,b=100米,r=20米,
代入(1)的式子得:300×100﹣π×202=30000﹣400π=30000﹣400×3.14=28744(米2),
答:广场空地的面积为28744米2.
25.在长江某段笔直的航道上依次有三个城市A、O、B,长江水流的方向为自西向东,水流的速度为每小时m千米,以O为原点建立数轴,取向东的方向为正方向,选取1千米为一个单位长度,A、B两城市所对应的数分别为a、b,满足|a+200|+(a+b)2=0.
(1)求A、B两个城市所对应的数;
(2)有两艘轮船P、Q分别从A、B两个城市同时出发相向而行,两船在静水中的速度分别为每小时40千米和每小时60千米,求P、Q两船相遇地点C所对应的数;
(3)在(2)的条件下,当m=10时,P、Q两船继续按原速原方向行驶,当Q到达A城市后,立即返回,两船都向东继续行驶,从相遇时刻起经过多长时间P、Q两船相距200千米?并直接写出此时P船在数轴上所对应的数.
【分析】(1)由非负数的性质可求a,b的值,即可求A,B两点所对应的数;
(2)设t小时相遇,根据题意列出方程,可求t的值,即可得相遇地点C所对应的数;
(3)分当Q到达A城市前,当Q到达A城市后两种情况讨论,列出方程可求时间,即可求P船在数轴上所对应的数.
【解答】解:(1)∵|a+200|+(a+b)2=0,
∴a+200=0,a+b=0.
解得a=﹣200,b=300,
∴A,B两个城市所对应的数分别是﹣200,300;
(2)设t小时相遇,
根据题意可得:(40+m+60﹣m)t=300﹣(﹣200),
∴t=5,
∴相遇地点C所对应的数=﹣200+5(40+m)=5m;
(3)当m=10,即相遇地点C所对应的数为50.
设从相遇时刻起经过x小时,P、Q两船相距200千米,
当Q到达A城市前,(40+10+60﹣10)x=200,
解得:x=2,符合题意,
P船在数轴上所对应的数为:50+50×2=150;
当Q到达A城市后,70(x﹣5)+200=50x+250 或 70(x﹣5)﹣200=50x+250,
解得:x=20或x=40,符合题意,
P船在数轴上所对应的数为:50+50×20=1050,或50+50×40=2050.
故从相遇时刻起经过2或20或40小时P、Q两船相距200千米,此时P船在数轴上所对应的数分别是150或1050或2050.
一.选择题(每题3分,共30分)
1.下列各对数中,数值相等的是( )
A.﹣27与(﹣2)7 B.﹣32与(﹣3)2
C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)3
2.x﹣y的相反数是( )
A.x+y B.﹣x﹣y C.y﹣x D.x﹣y
3.下列计算正确的是( )
A.4a﹣9a=5a B.a﹣a=a
C.a3﹣a2=a D.a+a=a2
4.如图,从上面看如图的几何体得到的平面图形是( )
A. B. C. D.
5.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
6.下面调查统计中,适合做全面调查的是( )
A.雪花牌电冰箱的市场占有率
B.蓓蕾专栏电视节目的收视率
C.飞马牌汽车每百公里的耗油量
D.今天班主任张老师与几名同学谈话
7.为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )
A.抽取的50名男生是总体
B.50名男生是样本容量
C.每一名男生的体重是个体
D.这种调查是全面调查
8.若a为有理数,则下列说法正确的是( )
A.﹣(a﹣2)2是负数 B.|a2+3|是正数
C.﹣1+(1﹣a)4是负数 D.以上说法都不对
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
10.下列说法不正确有( )个
(1)一个数的平方一定大于这个数;
(2)是有理数;
(3)一个数的平方一定小于这个数的绝对值;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是±1或0.
A.1 B.2 C.3 D.4
二.填空题:(每小题3分,共30分)
11.地球上的海洋面积约为36100000千米2,用科学记数法表示为 千米2.
12.的值是 .
13.若a2=4,|b|=3且a>b,则a﹣b= .
14.若x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,则正整数n的值为 .
15.已知关于x,y的多项式﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7不含二次项,则m+n= .
16.已知一个样本有100个数据,这组数据的最大值为36,最小值为12,如果组距取4,则把数据分成 组.
17.若定义一种新运算,规定=ad﹣bc,则= .
18.如果2x2﹣3x的值为﹣1,则6x﹣4x2+3的值为 .
19.火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x、y、z的箱子按如图所示的方式打包,则打包带的长至少为 .
20.在数轴上A、B两点分别表示的数是2和8,在数轴上,点A右侧有另外一点P到A、B的距离和是10,则点P表示的数是 .
三、解答题
21.计算:
(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2;
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×].
22.先化简,再求值:5ab﹣2[3ab﹣(4ab2+ab)]﹣5ab2,其中a=,b=﹣.
23.某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如图的两幅统计图:
(1)该调查小组共抽取了 名学生;
(2)样本学生中阳光体育运动时间为1.5小时的人数是 ,并补全频数分布直方图;
(3)请通过计算估计该市中小学生一天中阳光体育运动的平均时间.
24.如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为300米,宽为100米,圆形花坛的半径为20米,求广场空地的面积(π取3.14).
25.在长江某段笔直的航道上依次有三个城市A、O、B,长江水流的方向为自西向东,水流的速度为每小时m千米,以O为原点建立数轴,取向东的方向为正方向,选取1千米为一个单位长度,A、B两城市所对应的数分别为a、b,满足|a+200|+(a+b)2=0.
(1)求A、B两个城市所对应的数;
(2)有两艘轮船P、Q分别从A、B两个城市同时出发相向而行,两船在静水中的速度分别为每小时40千米和每小时60千米,求P、Q两船相遇地点C所对应的数;
(3)在(2)的条件下,当m=10时,P、Q两船继续按原速原方向行驶,当Q到达A城市后,立即返回,两船都向东继续行驶,从相遇时刻起经过多长时间P、Q两船相距200千米?并直接写出此时P船在数轴上所对应的数.
2019-2020学年黑龙江省哈尔滨工大附中六年级(下)月考数学试卷(4月份)(五四学制)
参考答案与试题解析
一.选择题(每题3分,共30分)
1.下列各对数中,数值相等的是( )
A.﹣27与(﹣2)7 B.﹣32与(﹣3)2
C.﹣3×23与﹣32×2 D.﹣(﹣3)2与﹣(﹣2)3
【分析】根据有理数乘方的法则对个选项的值进行逐一判断,找出数值相同的项.
【解答】解:A、根据有理数乘方的法则可知,(﹣2)7=﹣27,故A选项符合题意;
B、﹣32=﹣9,(﹣3)2=9,故B选项不符合题意;
C、﹣3×23=﹣24,﹣32×2=﹣18,故C选项不符合题意;
D、﹣(﹣3)2=﹣9,﹣(﹣2)3=8,故D选项不符合题意.
故选:A.
2.x﹣y的相反数是( )
A.x+y B.﹣x﹣y C.y﹣x D.x﹣y
【分析】根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:将x﹣y括起来,前面加一个“﹣”号,即可得到x﹣y的相反数﹣(x﹣y)=y﹣x.
故选:C.
3.下列计算正确的是( )
A.4a﹣9a=5a B.a﹣a=a
C.a3﹣a2=a D.a+a=a2
【分析】根据合并同类项的法则把系数相加即可.
【解答】解:A、系数相加字母及指数不变,故A不符合题意;
B、系数相加字母及指数不变,故B符合题意;
C、不是同类项不能合并,故C不符合题意;
D、系数相加字母及指数不变,故D不符合题意;
故选:B.
4.如图,从上面看如图的几何体得到的平面图形是( )
A. B. C. D.
【分析】从上面看得到从左往右2列,正方形的个数依次为2,1,依此画出图形即可.
【解答】解:根据几何体可得此图形的俯视图从左往右有2列,正方形的个数依次为2,1.
故选:A.
5.在式子,2πx2y,,y2﹣5,π+6,中,多项式的个数是( )
A.1 B.2 C.3 D.4
【分析】根据由几个单项式的和组成的式子叫多项式解答即可.
【解答】解:在式子,2πx2y,,y2﹣5,π+6,中,
多项式有:,y2﹣5,共2个.
故选:B.
6.下面调查统计中,适合做全面调查的是( )
A.雪花牌电冰箱的市场占有率
B.蓓蕾专栏电视节目的收视率
C.飞马牌汽车每百公里的耗油量
D.今天班主任张老师与几名同学谈话
【分析】适合普查的方式一般有以下几种:
①范围较小;②容易掌控;③不具有破坏性;
④可操作性较强.
【解答】解:A、B、C中,容量太大,不易做全面调查,故选D.
7.为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )
A.抽取的50名男生是总体
B.50名男生是样本容量
C.每一名男生的体重是个体
D.这种调查是全面调查
【分析】根据总体的定义判断A,总体:所要考察对象的全体;
根据样本容量的定义判断B,个体:每一个考察对象;
根据个体的定义判断C,样本:从总体中抽取的部分考察对象称为样本;
根据普查的定义判断D,普查就是都查一遍,比如全国人口普查,就是把中国所有的人都点一遍.抽查就是抽取其中的一部分来检查统计,适用于破坏性或者工作量大的统计调查工作.
【解答】解:A、级498名男生的体重是全体,故本选项不合题意;
B、50是样本容量,故本选项不合题意;
C、每一名男生的体重是个体,故本选项符合题意;
D、从七年级498名学生中抽取50名学生进行测量,这种调查是抽样调查,故本选项符合题意.
故选:C.
8.若a为有理数,则下列说法正确的是( )
A.﹣(a﹣2)2是负数 B.|a2+3|是正数
C.﹣1+(1﹣a)4是负数 D.以上说法都不对
【分析】利用偶次幂和绝对值都具有非负性解答即可.
【解答】解:A、﹣(a﹣2)2是负数,说法错误,例如a=2时,﹣(a﹣2)2是零,不是负数;
B、|a2+3|是正数,说法正确;
C、﹣1+(1﹣a)4是负数,说法错误,例如a=1,﹣1+(1﹣a)4是零;
D、以上说法都不对,说法错误;
故选:B.
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:因圆柱的展开面为长方形,AC展开应该是两直线,且有公共点C.
故选:B.
10.下列说法不正确有( )个
(1)一个数的平方一定大于这个数;
(2)是有理数;
(3)一个数的平方一定小于这个数的绝对值;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是±1或0.
A.1 B.2 C.3 D.4
【分析】根据有理数的乘方、有理数和绝对值的性质分别对每一项进行分析,即可得出答案.
【解答】解:(1)一个数的平方为正数与0,不一定都大于这个数;
(2)是有理数;
(3)一个数的平方不一定小于这个数的绝对值,例如,(﹣1)2=|﹣1|;
(4)一个数的平方不可能为负数;
(5)平方等于本身的数是1或0;
其中不正确有3个;
故选:C.
二.填空题:(每小题3分,共30分)
11.地球上的海洋面积约为36100000千米2,用科学记数法表示为 3.61×107 千米2.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:将36100000用科学记数法表示为:3.61×107.
故答案为:3.61×107.
12.的值是 .
【分析】积的乘方,等于每个因式乘方的积,据此计算即可.
【解答】解:
=
=
=
=
=
=.
故答案为:.
13.若a2=4,|b|=3且a>b,则a﹣b= 1或5 .
【分析】先根据已知条件确定a、b的值,再计算a﹣b.
【解答】解:∵a2=4,|b|=3,
∴a=±2,b=±3.
由a>b,可得a=2,b=±3.
当a=2,b=﹣3时,a﹣b=2+3=5;
当a=﹣2,b=﹣3时,a﹣b=﹣2﹣(﹣3)=1.
故答案为:1或5.
14.若x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,则正整数n的值为 2或1 .
【分析】根据多项式的次数定义和n是正整数得出4+n=6或4+n=5,求出n的值即可.
【解答】解:∵x2y3﹣0.1x4yn+xy5是关于x,y的六次多项式,
又∵n是正整数,
∴4+n=6或4+n=5,
∴n=2或n=1;
故答案为:2或1.
15.已知关于x,y的多项式﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7不含二次项,则m+n= ﹣1.5 .
【分析】先合并同类项,然后根据多项式不含二次项可知5m=0,2n+3=0,从而可求得m、n的值,然后代入计算即可.
【解答】解:﹣5x2y﹣2nxy+5my2﹣3xy+4x﹣7=﹣5x2y﹣(2n+3)xy+5my2+4x﹣7,
∵多项式不含二次项,
∴5m=0,2n+3=0,
解得m=0,n=﹣1.5,
∴m+n=﹣1.5,
故答案为:﹣1.5.
16.已知一个样本有100个数据,这组数据的最大值为36,最小值为12,如果组距取4,则把数据分成 6 组.
【分析】根据题意和题目中的数据,可以计算出要分成几组.
【解答】解:36﹣12=24,
24÷4=6,
即这些数据要分成6组,
故答案为:6.
17.若定义一种新运算,规定=ad﹣bc,则= ﹣43 .
【分析】根据=ad﹣bc,用5与﹣2的积减去﹣3与﹣11的积,求出的值是多少即可.
【解答】解:∵=ad﹣bc,
∴
=5×(﹣2)﹣(﹣3)×(﹣11)
=﹣10﹣33
=﹣43.
故答案为:﹣43.
18.如果2x2﹣3x的值为﹣1,则6x﹣4x2+3的值为 5 .
【分析】首先把6x﹣4x2+3化成﹣2(2x2﹣3x)+3,然后把2x2﹣3x=﹣1代入化简后的算式求解即可.
【解答】解:∵2x2﹣3x=﹣1,
∴6x﹣4x2+3
=﹣2(2x2﹣3x)+3
=﹣2×(﹣1)+3
=2+3
=5.
故答案为:5.
19.火车站和汽车站都为旅客提供打包服务,如果长、宽、高分别为x、y、z的箱子按如图所示的方式打包,则打包带的长至少为 4y+6z+2x .
【分析】本题实际上就是求长方体的侧面的周长.
【解答】解:根据题意,得
2×(y+z)×2+2×(z+x)=4y+6z+2x.
故答案为:4y+6z+2x.
20.在数轴上A、B两点分别表示的数是2和8,在数轴上,点A右侧有另外一点P到A、B的距离和是10,则点P表示的数是 10 .
【分析】根据数轴上两点距离的计算方法,列方程求解即可.
【解答】解:∵数轴上A、B两点分别表示的数是2和8,
∴AB=|8﹣2|=6,
又∵点A右侧有另外一点P到A、B的距离和是10,
∴点P在点B的右侧,
设点P所表示的数为x,
则(x﹣2)+(x﹣8)=10,
解得x=10,
故答案为:10.
三、解答题
21.计算:
(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2;
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×].
【分析】(1)首先计算乘方,然后从左向右依次计算,求出算式的值是多少即可.
(2)首先计算乘方和中括号里面的运算,然后计算中括号外面的乘法,求出算式的值是多少即可.
【解答】解:(1)(﹣3)÷(﹣)×0.75×||÷|﹣3|2
=×××
=.
(2)﹣32××[(﹣5)2×(﹣)﹣240÷(﹣4)×]
=﹣3×[25×(﹣)+60×]
=﹣3×(﹣15+15)
=﹣3×0
=0.
22.先化简,再求值:5ab﹣2[3ab﹣(4ab2+ab)]﹣5ab2,其中a=,b=﹣.
【分析】原式去括号合并得到最简结果,将a与b的值代入计算即可求出值.
【解答】解:原式=5ab﹣6ab+8ab2+ab﹣5ab2=3ab2,
当a=,b=﹣时,原式=.
23.某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如图的两幅统计图:
(1)该调查小组共抽取了 500 名学生;
(2)样本学生中阳光体育运动时间为1.5小时的人数是 120 ,并补全频数分布直方图;
(3)请通过计算估计该市中小学生一天中阳光体育运动的平均时间.
【分析】(1)利用0.5小时的人数为:100人,所占比例为:20%,即可求出样本容量;
(2)利用样本容量乘以1.5小时的百分数,即可求出1.5小时的人数,画图即可;
(3)计算出该市中小学生一天中阳光体育运动的平均时间即可.
【解答】解:(1)由题意可得:0.5小时的人数为:100人,所占比例为:20%,
100÷20%=500,
∴本次调查共抽样了500名学生;
故答案为500;
(2)1.5小时的人数为:500×24%=120(人)
故答案为120,
如图所示:
(3)根据题意得:=1.18,即该市中小学生一天中阳光体育运动的平均时间约1小时.
24.如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为a米,宽为b米.
(1)请列式表示广场空地的面积;
(2)若休闲广场的长为300米,宽为100米,圆形花坛的半径为20米,求广场空地的面积(π取3.14).
【分析】(1)根据广场空地的面积等于长方形的面积减去四个四分之一圆形的花坛的面积即可得;
(2)根据题(1)的结论,将相应的数代入计算即可得.
【解答】解:(1)矩形的面积为ab,
四分之一圆形的花坛的面积为πr2,
则广场空地的面积为ab﹣4×πr2=ab﹣πr2,
答:广场空地的面积为(ab﹣πr2)米2;
(2)由题意得:a=300米,b=100米,r=20米,
代入(1)的式子得:300×100﹣π×202=30000﹣400π=30000﹣400×3.14=28744(米2),
答:广场空地的面积为28744米2.
25.在长江某段笔直的航道上依次有三个城市A、O、B,长江水流的方向为自西向东,水流的速度为每小时m千米,以O为原点建立数轴,取向东的方向为正方向,选取1千米为一个单位长度,A、B两城市所对应的数分别为a、b,满足|a+200|+(a+b)2=0.
(1)求A、B两个城市所对应的数;
(2)有两艘轮船P、Q分别从A、B两个城市同时出发相向而行,两船在静水中的速度分别为每小时40千米和每小时60千米,求P、Q两船相遇地点C所对应的数;
(3)在(2)的条件下,当m=10时,P、Q两船继续按原速原方向行驶,当Q到达A城市后,立即返回,两船都向东继续行驶,从相遇时刻起经过多长时间P、Q两船相距200千米?并直接写出此时P船在数轴上所对应的数.
【分析】(1)由非负数的性质可求a,b的值,即可求A,B两点所对应的数;
(2)设t小时相遇,根据题意列出方程,可求t的值,即可得相遇地点C所对应的数;
(3)分当Q到达A城市前,当Q到达A城市后两种情况讨论,列出方程可求时间,即可求P船在数轴上所对应的数.
【解答】解:(1)∵|a+200|+(a+b)2=0,
∴a+200=0,a+b=0.
解得a=﹣200,b=300,
∴A,B两个城市所对应的数分别是﹣200,300;
(2)设t小时相遇,
根据题意可得:(40+m+60﹣m)t=300﹣(﹣200),
∴t=5,
∴相遇地点C所对应的数=﹣200+5(40+m)=5m;
(3)当m=10,即相遇地点C所对应的数为50.
设从相遇时刻起经过x小时,P、Q两船相距200千米,
当Q到达A城市前,(40+10+60﹣10)x=200,
解得:x=2,符合题意,
P船在数轴上所对应的数为:50+50×2=150;
当Q到达A城市后,70(x﹣5)+200=50x+250 或 70(x﹣5)﹣200=50x+250,
解得:x=20或x=40,符合题意,
P船在数轴上所对应的数为:50+50×20=1050,或50+50×40=2050.
故从相遇时刻起经过2或20或40小时P、Q两船相距200千米,此时P船在数轴上所对应的数分别是150或1050或2050.
同课章节目录
