新人教版数学七年级上 第2章《整式的加减》复习教学设计
文档属性
| 名称 | 新人教版数学七年级上 第2章《整式的加减》复习教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 35.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-05 19:32:46 | ||
图片预览


文档简介
第2章《整式的加减》复习
【教学目标】:
知识与技能:
1、理解整式、单项式、多项式的概念,对于给出的式子,会确定是不是整式、单项式、多项式,并能指明单项式的系数、次数、多项式的项数、次数,会把一个多项式按某一个字母的降幂或升幂排列。
2、会判断给出的项是不是同类项,掌握合并同类项的要点,会熟练地合并同类项。
3、 能熟练的运用去括号、添括号、合并同类项的法则,进行整式的加减运算.
过程与方法:提高学生概念的辨别能力以及整式加减的运算能力.
情感与态度:感受细心对解决好问题很有帮助.
【教学重点】:运用法则进行整式的加减.
【教学难点】:当括号外面有负因数时去括号.
【教材教法】:分析例题,归纳法则,点拨提升.
【教学突破点】 :错题分析,分类型复习
【课型】: 复习课 (说明:题量较大,可根据实际情况酌情选用)
【教学过程】:
. “复习与小结”是进行有效学习的重要方法,它既能使学生有目的地梳理所学知识,形成知识体系,又能促使学生反思知识获得的过程,形成自己对所学知识较为深刻而独特的理解。学生在此过程中还能提高自己的归纳、概括等能力,形成反思的意识。教师应引导学生进行独立思考,然后与同伴进行交流。在学生充分交流的基础上,教师可引导学生明确下面的内容:
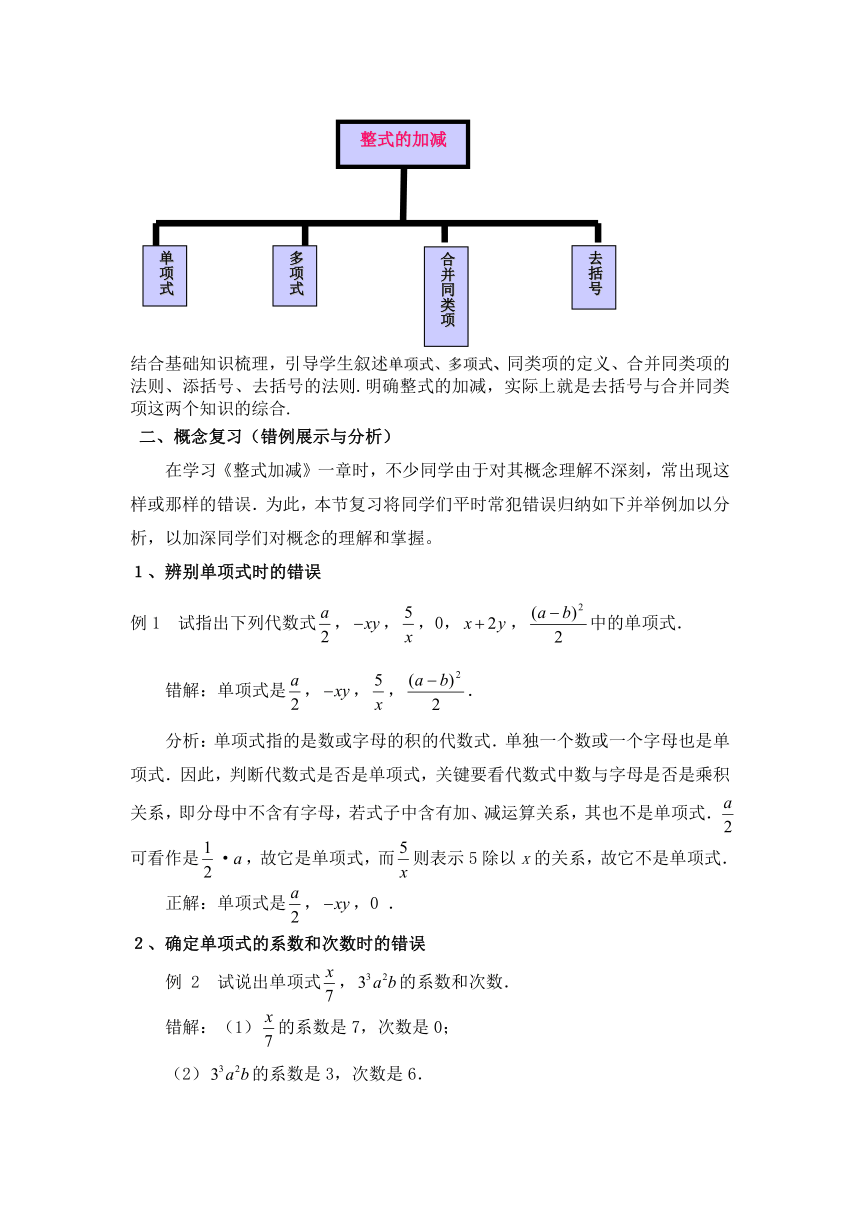
一、本章内容框架图
结合基础知识梳理,引导学生叙述单项式、多项式、同类项的定义、合并同类项的法则、添括号、去括号的法则.明确整式的加减,实际上就是去括号与合并同类项这两个知识的综合.
二、概念复习(错例展示与分析)
在学习《整式加减》一章时,不少同学由于对其概念理解不深刻,常出现这样或那样的错误.为此,本节复习将同学们平时常犯错误归纳如下并举例加以分析,以加深同学们对概念的理解和掌握。
1、辨别单项式时的错误
例1 试指出下列代数式,,,0,,中的单项式.
错解:单项式是,,,.
分析:单项式指的是数或字母的积的代数式.单独一个数或一个字母也是单项式.因此,判断代数式是否是单项式,关键要看代数式中数与字母是否是乘积关系,即分母中不含有字母,若式子中含有加、减运算关系,其也不是单项式.可看作是·,故它是单项式,而则表示5除以x的关系,故它不是单项式.
正解:单项式是,,0 .
2、确定单项式的系数和次数时的错误
例 2 试说出单项式,的系数和次数.
错解:(1)的系数是7,次数是0;
(2)的系数是3,次数是6.
分析:单项式的系数:是指单项式中的数字因数;单项数的次数:是指单项式中所有字母的指数的和.
正确答案是:的系数是,次数是1;的系数是33,次数是3.
3、辨别多项式时的错误
例 3 试指出下列代数式,,中的多项式.
错解:多项式是,.
分析:几个单项式的和叫做多项式. 因此,判断代数式是否是多项式,关键要看代数式中的每一项是否是单项式. 中不是单项式,故它不是多项式; =,故它是多项式.
正解:多项式是,.
4、确定多项式的次数和项时的错误
例 4 试说出多项式的次数、三次项、二次项以及一次项的系数和常数项.
错解:此多项式的次数是4次,三次项是和,二次项是和,一次项的系数5,常数项是7 .
分析:错解的原因:一是没有理解单项式的定义;二是对多项式的次数和项的定义理解不清.多项式的次数是指多项式里次数最高项的次数,这里是次数最高项,其次数是6;多项式的项是指在多项式中,每一个单项式.特别注意多项式的项包括它前面的性质符号.
正解:此多项式的次数是 6次,三次项是和,二次项是,一次项的系数,常数项是.
5、判断同类项时的错误
例 5 试判断下列各组单项式是否是同类项:
①3x3y2与—5x2y3 ;②4ab2与—2xy2; ③3x3y2与—y2x3.
错解:①、②、③都是同类项.
分析:由于同类项必须同时满足两个条件:(1)所含字母相同;(2)相同字母的次数相同,二者缺一不可.同类项与系数大小、字母的排列顺序无关.这里3x3y2与—5x2y3字母相同而相同字母的次数不同,故不是同类项;4ab2与—2xy2由于字母不同,故也不是同类项.
正解:只有③是同类项.
6、合并同类项时的错误
例 6 下列各题合并同类项的结果是否正确?
①3a3 + 2a3 = 5a6; ②3x2 + 2x3 = 5x5;
③5y2 — 3y2 = 2; ④ 4x2y — 5y2x = — x2y .
错解:①②③④都正确.
分析:合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母和字母指数不变.错解的原因是:(1)合并同类项时,把字母的次数相加,如①;(2)合并同类项时,把字母及字母的次数漏掉,如③;(3)不是同类项不能合并,如②④.正确答案是:都错误.
8、去括号时的错误
例 7 计算:(1)(8a — 7b)—(4a — 5b);
(2)(5x2 — 2x + 3)—3(x2 — 2x +1).
错解:(1)原式 = 8a — 7b — 4a — 5b = 4a — 12b;
(2)原式 = 5x2 — 2x + 3 —3x2 — 2x + 1 = 2x2— 4x + 4.
分析:(1)错解的原因是:由去括号法则知,括号前面是“ — ”号,把括号和它前面的“ —”号去掉,括号里的各项都改变符号.而只改变第一项的符号;(2)错解的原因有二:①去括号时,括号前面的系数应乘括号内的每一项,而只乘了括号内的第一项;②括号前面是“— ”号,却只改变第一项的符号.
正解:(1)原式 = 8a —7b — 4a + 5b = 4a — 2b;
(2)原式 = 5x2— 2x + 3— 3x2 + 6x — 3 = 2x2 + 4x.
三、整式的加减基本运算(例题讲解)
1、单项式的和
例1、求单项式5x2y,-2x2y,-2xy2 ,4x2y的和.
分析:求几个单项式的和,要先用加号将几个单项式连成和的形式,若某个单项式前面是负号,在和式中要连同负号一起用括号括起来,然后去括号,再合并同类项.
解: 5x2y +(-2x2y)+(- 2xy2 )+ 4x2y------------- 添括号
= 5x2y - 2x2y - 2xy2 +4x2y-------------------------去括号
=( 5x2y - 2x2y +4x2y)- 2xy2----------------------结合同类项
= 7x2y - 2xy2--------------------------------------合并同类项
2、求几个多项式的和或差
例2 求整式x2—5x—3与—2x2+3x—2的差.
分析:求几个多项式的和或差,要先将每个多项式用括号括起来,并用加号或减号连接,然后按照去括号,合并同类项的法则进行运算.注意:求“……”与“……”的差,“与”字前面的是被减式.
解:(x2—5x—3)—(—2x2+3x—2) -----------------------------添括号
=x2—5x—3+2x2—3x+2-------------------------------------去括号
=(x2+2x2)+(—5x—3x)+(—3+2)---------------------结合同类项
=3x2—8x—1----------------------------合并同类项
变式:
(1)若两个单项式的和是2x2+xy+3y2,一个加式是x2-xy,求另一个加式.
(2)已知某多项式与3x2-6x+5的差是4x 2+7x-6,求此多项式.
3、括号前带乘数的整式的加减
例3、计算6x2—4(2x2+3x—1)
分析:在整式的加减中,若某个括号前带有乘数,为了避免出现错误,可先将此数与括号内每一项相乘,再去括号.
解: 6x2—4(2x2+3x—1)
=6x2—(8x2+12x—4)
=6x2—8x2—12x+4
=—2x2—12x+4.
变式:
1、已知:A=3xm+ym,B=2ym-xm,C=5xm -7ym. 求:1)A -B -C ; 2)2A -3C
2、有两个多项式:A=2a2 -4a+1,B=(2a2 -2a)+3,当a取任意有理数时,能比较A与B的大小吗
4、先化简,后求值
例4、 先化简,再求值
5(3x2y—xy2)—(xy2+3x2y).其中x=,y=—1.
解: 5(3x2y—xy2)—(xy2+3x2y)
=15x2y—5xy2—xy2—3x2y
=12x2y—6xy2.
当x=,y=—1时,原式=12×()2×(—1)—6××(—1)2
=—3—3
=—6.
5、整体思想的应用
例5 、已知x=y+3,求代数式(x—y)2—的值.
分析:在整式的加减中,有时根据式子的特点,将整式中的“部分”看成一个整体,可给运算带来方便.
解:(x—y)2+
=(x—y)2+(x—y)+2
当x=y+3,即x—y=3时,原式=32+3+2=14.
归纳整式加减的一般步骤:
1、如果遇到括号按去括号法则先去括号.
2、结合同类项.
3、合并同类项
四、课堂小结
以你在学习第2章《整式的加减》的经验教训,对同学们提几点建议.
五、作业
1、求单项式5x2y,2x2y,2xy2,4x2y的和.
2、求单项式单项式4x,—11x2,—5x,8x2,—3的和
3、求5x2y + 2x2y与 2xy2 + 4x2y的和.
4、求5x2y - 2x2y 与- 2xy2 + 4x2y的和.
5、求5x2y - 2x2y 与 - 2xy2 + 4x2y的差
6、先化简,再求值:
其中x=-2,y=-3,Z=1.
选做题:
若代数式2x2+3y+7的值是8,那么代数式4x2+6y+9的值是 .
提示:观察 2x2+3y+7和 4x2+6y+9的字母部分有何联系,或许你能找到解决问题的办法.
合并同类项
整式的加减
单项式
多项式
去括号
【教学目标】:
知识与技能:
1、理解整式、单项式、多项式的概念,对于给出的式子,会确定是不是整式、单项式、多项式,并能指明单项式的系数、次数、多项式的项数、次数,会把一个多项式按某一个字母的降幂或升幂排列。
2、会判断给出的项是不是同类项,掌握合并同类项的要点,会熟练地合并同类项。
3、 能熟练的运用去括号、添括号、合并同类项的法则,进行整式的加减运算.
过程与方法:提高学生概念的辨别能力以及整式加减的运算能力.
情感与态度:感受细心对解决好问题很有帮助.
【教学重点】:运用法则进行整式的加减.
【教学难点】:当括号外面有负因数时去括号.
【教材教法】:分析例题,归纳法则,点拨提升.
【教学突破点】 :错题分析,分类型复习
【课型】: 复习课 (说明:题量较大,可根据实际情况酌情选用)
【教学过程】:
. “复习与小结”是进行有效学习的重要方法,它既能使学生有目的地梳理所学知识,形成知识体系,又能促使学生反思知识获得的过程,形成自己对所学知识较为深刻而独特的理解。学生在此过程中还能提高自己的归纳、概括等能力,形成反思的意识。教师应引导学生进行独立思考,然后与同伴进行交流。在学生充分交流的基础上,教师可引导学生明确下面的内容:
一、本章内容框架图
结合基础知识梳理,引导学生叙述单项式、多项式、同类项的定义、合并同类项的法则、添括号、去括号的法则.明确整式的加减,实际上就是去括号与合并同类项这两个知识的综合.
二、概念复习(错例展示与分析)
在学习《整式加减》一章时,不少同学由于对其概念理解不深刻,常出现这样或那样的错误.为此,本节复习将同学们平时常犯错误归纳如下并举例加以分析,以加深同学们对概念的理解和掌握。
1、辨别单项式时的错误
例1 试指出下列代数式,,,0,,中的单项式.
错解:单项式是,,,.
分析:单项式指的是数或字母的积的代数式.单独一个数或一个字母也是单项式.因此,判断代数式是否是单项式,关键要看代数式中数与字母是否是乘积关系,即分母中不含有字母,若式子中含有加、减运算关系,其也不是单项式.可看作是·,故它是单项式,而则表示5除以x的关系,故它不是单项式.
正解:单项式是,,0 .
2、确定单项式的系数和次数时的错误
例 2 试说出单项式,的系数和次数.
错解:(1)的系数是7,次数是0;
(2)的系数是3,次数是6.
分析:单项式的系数:是指单项式中的数字因数;单项数的次数:是指单项式中所有字母的指数的和.
正确答案是:的系数是,次数是1;的系数是33,次数是3.
3、辨别多项式时的错误
例 3 试指出下列代数式,,中的多项式.
错解:多项式是,.
分析:几个单项式的和叫做多项式. 因此,判断代数式是否是多项式,关键要看代数式中的每一项是否是单项式. 中不是单项式,故它不是多项式; =,故它是多项式.
正解:多项式是,.
4、确定多项式的次数和项时的错误
例 4 试说出多项式的次数、三次项、二次项以及一次项的系数和常数项.
错解:此多项式的次数是4次,三次项是和,二次项是和,一次项的系数5,常数项是7 .
分析:错解的原因:一是没有理解单项式的定义;二是对多项式的次数和项的定义理解不清.多项式的次数是指多项式里次数最高项的次数,这里是次数最高项,其次数是6;多项式的项是指在多项式中,每一个单项式.特别注意多项式的项包括它前面的性质符号.
正解:此多项式的次数是 6次,三次项是和,二次项是,一次项的系数,常数项是.
5、判断同类项时的错误
例 5 试判断下列各组单项式是否是同类项:
①3x3y2与—5x2y3 ;②4ab2与—2xy2; ③3x3y2与—y2x3.
错解:①、②、③都是同类项.
分析:由于同类项必须同时满足两个条件:(1)所含字母相同;(2)相同字母的次数相同,二者缺一不可.同类项与系数大小、字母的排列顺序无关.这里3x3y2与—5x2y3字母相同而相同字母的次数不同,故不是同类项;4ab2与—2xy2由于字母不同,故也不是同类项.
正解:只有③是同类项.
6、合并同类项时的错误
例 6 下列各题合并同类项的结果是否正确?
①3a3 + 2a3 = 5a6; ②3x2 + 2x3 = 5x5;
③5y2 — 3y2 = 2; ④ 4x2y — 5y2x = — x2y .
错解:①②③④都正确.
分析:合并同类项的法则是:同类项的系数相加,所得的结果作为系数,字母和字母指数不变.错解的原因是:(1)合并同类项时,把字母的次数相加,如①;(2)合并同类项时,把字母及字母的次数漏掉,如③;(3)不是同类项不能合并,如②④.正确答案是:都错误.
8、去括号时的错误
例 7 计算:(1)(8a — 7b)—(4a — 5b);
(2)(5x2 — 2x + 3)—3(x2 — 2x +1).
错解:(1)原式 = 8a — 7b — 4a — 5b = 4a — 12b;
(2)原式 = 5x2 — 2x + 3 —3x2 — 2x + 1 = 2x2— 4x + 4.
分析:(1)错解的原因是:由去括号法则知,括号前面是“ — ”号,把括号和它前面的“ —”号去掉,括号里的各项都改变符号.而只改变第一项的符号;(2)错解的原因有二:①去括号时,括号前面的系数应乘括号内的每一项,而只乘了括号内的第一项;②括号前面是“— ”号,却只改变第一项的符号.
正解:(1)原式 = 8a —7b — 4a + 5b = 4a — 2b;
(2)原式 = 5x2— 2x + 3— 3x2 + 6x — 3 = 2x2 + 4x.
三、整式的加减基本运算(例题讲解)
1、单项式的和
例1、求单项式5x2y,-2x2y,-2xy2 ,4x2y的和.
分析:求几个单项式的和,要先用加号将几个单项式连成和的形式,若某个单项式前面是负号,在和式中要连同负号一起用括号括起来,然后去括号,再合并同类项.
解: 5x2y +(-2x2y)+(- 2xy2 )+ 4x2y------------- 添括号
= 5x2y - 2x2y - 2xy2 +4x2y-------------------------去括号
=( 5x2y - 2x2y +4x2y)- 2xy2----------------------结合同类项
= 7x2y - 2xy2--------------------------------------合并同类项
2、求几个多项式的和或差
例2 求整式x2—5x—3与—2x2+3x—2的差.
分析:求几个多项式的和或差,要先将每个多项式用括号括起来,并用加号或减号连接,然后按照去括号,合并同类项的法则进行运算.注意:求“……”与“……”的差,“与”字前面的是被减式.
解:(x2—5x—3)—(—2x2+3x—2) -----------------------------添括号
=x2—5x—3+2x2—3x+2-------------------------------------去括号
=(x2+2x2)+(—5x—3x)+(—3+2)---------------------结合同类项
=3x2—8x—1----------------------------合并同类项
变式:
(1)若两个单项式的和是2x2+xy+3y2,一个加式是x2-xy,求另一个加式.
(2)已知某多项式与3x2-6x+5的差是4x 2+7x-6,求此多项式.
3、括号前带乘数的整式的加减
例3、计算6x2—4(2x2+3x—1)
分析:在整式的加减中,若某个括号前带有乘数,为了避免出现错误,可先将此数与括号内每一项相乘,再去括号.
解: 6x2—4(2x2+3x—1)
=6x2—(8x2+12x—4)
=6x2—8x2—12x+4
=—2x2—12x+4.
变式:
1、已知:A=3xm+ym,B=2ym-xm,C=5xm -7ym. 求:1)A -B -C ; 2)2A -3C
2、有两个多项式:A=2a2 -4a+1,B=(2a2 -2a)+3,当a取任意有理数时,能比较A与B的大小吗
4、先化简,后求值
例4、 先化简,再求值
5(3x2y—xy2)—(xy2+3x2y).其中x=,y=—1.
解: 5(3x2y—xy2)—(xy2+3x2y)
=15x2y—5xy2—xy2—3x2y
=12x2y—6xy2.
当x=,y=—1时,原式=12×()2×(—1)—6××(—1)2
=—3—3
=—6.
5、整体思想的应用
例5 、已知x=y+3,求代数式(x—y)2—的值.
分析:在整式的加减中,有时根据式子的特点,将整式中的“部分”看成一个整体,可给运算带来方便.
解:(x—y)2+
=(x—y)2+(x—y)+2
当x=y+3,即x—y=3时,原式=32+3+2=14.
归纳整式加减的一般步骤:
1、如果遇到括号按去括号法则先去括号.
2、结合同类项.
3、合并同类项
四、课堂小结
以你在学习第2章《整式的加减》的经验教训,对同学们提几点建议.
五、作业
1、求单项式5x2y,2x2y,2xy2,4x2y的和.
2、求单项式单项式4x,—11x2,—5x,8x2,—3的和
3、求5x2y + 2x2y与 2xy2 + 4x2y的和.
4、求5x2y - 2x2y 与- 2xy2 + 4x2y的和.
5、求5x2y - 2x2y 与 - 2xy2 + 4x2y的差
6、先化简,再求值:
其中x=-2,y=-3,Z=1.
选做题:
若代数式2x2+3y+7的值是8,那么代数式4x2+6y+9的值是 .
提示:观察 2x2+3y+7和 4x2+6y+9的字母部分有何联系,或许你能找到解决问题的办法.
合并同类项
整式的加减
单项式
多项式
去括号
