新人教版数学七年级上 第一章§1.2《有理数》教案(5课时)
文档属性
| 名称 | 新人教版数学七年级上 第一章§1.2《有理数》教案(5课时) |  | |
| 格式 | zip | ||
| 文件大小 | 54.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-05 20:41:54 | ||
图片预览




文档简介
第一章§1.2《有理数》教案(5课时)
§1.2.1有理数;
[学情分析]有理数是学生在学习了自然数和小数等的概念上的一次扩展,它不仅是整个中学学生学习的基础,而且也是学生在日常生活中最常见的数学概念。
[教学目标]
1.知识与技能
①理解有理数的意义.
②能把给出的有理数按要求分类.
③了解0在有理数分类的作用.
2.过程与方法
经历本节的学习,培养学生树立分类讨论的观点和能正确地进行分类的能力.
3.情感、态度与价值观
通过联系与发展、对立与统一的思考方法对学生进行辩证唯物主义教育.
[教学重点]理解有理数的概念。
[教学难点]掌握有理数的两种分类.
[教学策略]由于有理数的概念较易被学生理解,而前一段的教学内容刚刚引进了负数的概念,因此可以把这部分的内容提前到学完负数之后。并可以向学生展示数的扩展示意图:
[教与学互动设计]
(一)创设情境,导入新课
接球游戏:在游戏过程中,发现数字不够用了,引出负数概念
(二)合作交流,解读探究
学生列举,如:3,5.7,-7,-9,-10,0,,,-3, -7.4,5.2…
议一议 你能说说这些数的特点吗?
学生回答,并相互补充:有小学学过的整数、0、分数,也有负整数、负分数.
说明:我们把所有的这些数统称为有理数.
试一试 你能对以上各种类型的数作出一张分类表吗?
有理数
说明:以上分类,若学生思考有困难,可加以引导:因为整数和分数统称为有理数,所以有理数可分为整数和分数两大类,那么整数又包含那些数?分数呢?
做一做 以上按整数和分数来分,那可不可以按性质(正数、负数)来分呢,试一试.
有理数
(3)数的集合
把所有正数组成的集合,叫做正数集合.
试一试 试着归纳总结,什么是负数集合、整数集合、分数集合、有理数集合.
(三)应用迁移,巩固提高
例1 把下列各数填入相应的集合内:
,3.1416,0,2004,-,-0.23456,10%,10.l,0.67,-89
正数集合 负数集合 整数集合 分数集合
例2 以下是两位同学的分类方法,你认为他们的分类的结果正确吗?为什么?
有理数 有理数
[点评] 以上是对各类有理数的特点及有理数的分类进行的训练,基础性强,需要重视
例3下列说法正确的是(B)
①0是最小的正整数 ②0是最小的有理数
③0不是负数 ④0既是非正数,也是非负数
A.1个 B.2个 C.3个 D.4个
例4 如果用字母表示一个数,那a可能是什么样的数,一定为正数吗?与你的伙伴交流一下你的看法.
[点评] 此题开放性较强.同时,要求学生能用分类的思想对a全面认识.
(四)总结反思,拓展升华
提问:今天你获得了哪些知识?
由学生自己小结,然后教师总结:今天我们学习了有理数的定义和两种分类的方法.我们要能正确地判断一个数属于哪一类,要特别注意“0”的正确说法.
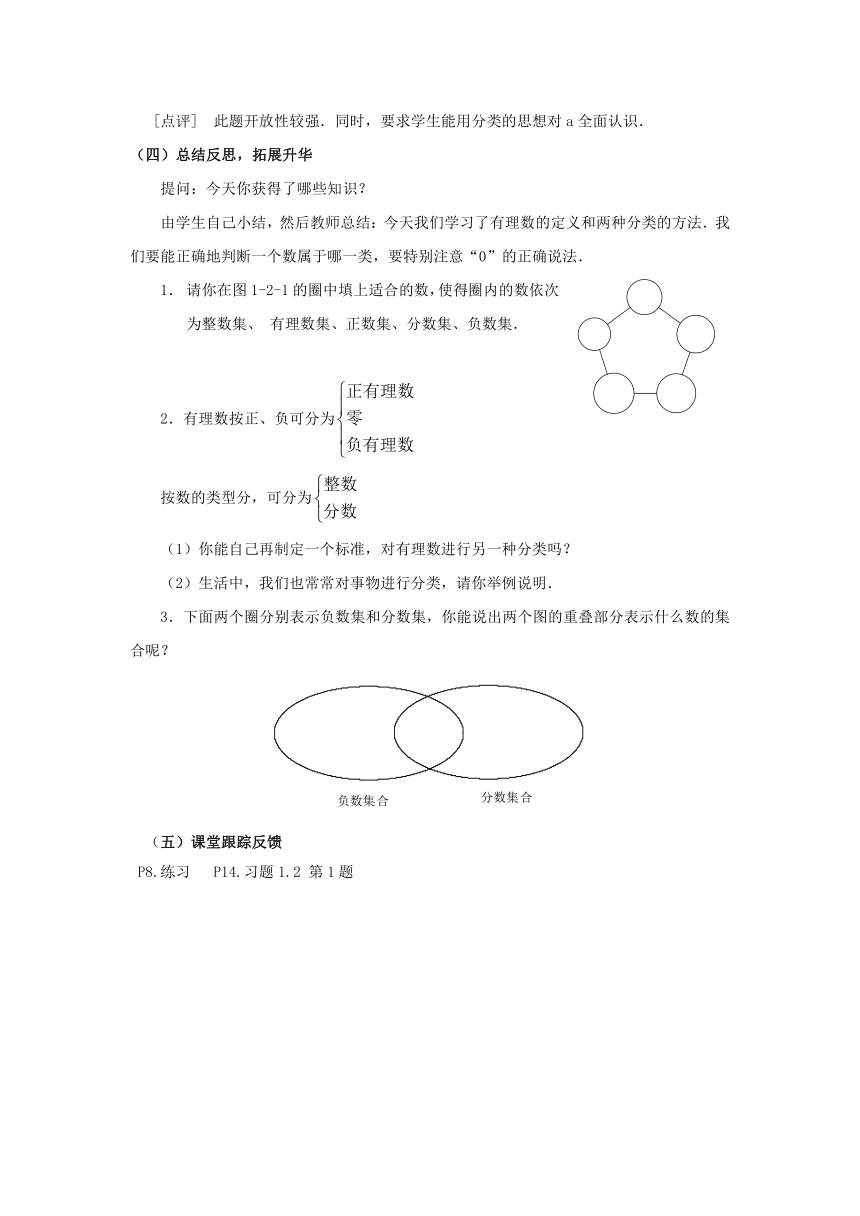
请你在图1-2-1的圈中填上适合的数,使得圈内的数依次为整数集、有理数集、正数集、分数集、负数集.
2.有理数按正、负可分为
按数的类型分,可分为
(1)你能自己再制定一个标准,对有理数进行另一种分类吗?
(2)生活中,我们也常常对事物进行分类,请你举例说明.
3.下面两个圈分别表示负数集和分数集,你能说出两个图的重叠部分表示什么数的集合呢?
(五)课堂跟踪反馈
P8.练习 P14.习题1.2 第1题
§1.2.2数轴:
[学情分析]数轴概念是数形结合的基础,是帮助学生理解数学、学好数学的重要思想方法。,本节后面的相反数等的概念和运算都是结合数轴进行的,由此可见学生学好数轴概念的重要性。数轴是用“长度”度量各类量的抽象,日常生活中常见的用温度计度量温度,用弹簧称(刻度在直线上)称重量等,都已为学生学习数轴概念打下了基础。在教学中,数轴的三要素都要将认真分析它的作用,使学生从直观认识上升到理性认识。
[教学目标]
1、知识目标:①掌握数轴三要素,能正确画出数轴.
②能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数.
2、过程与方法目标:
①使学生受到把实际问题抽象成数学问题的训练,逐步形成应用数学的意识.
②结合本节内容,对学生渗透数形结合的重要思想方法.
3.情感与能力目标:
使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点.
[教学重难点]
重点:数轴的概念.
难点:从直观认识到理性认识,从而建立数轴概念.
[教与学互动设计]
(一)创设情境,导入新课
情景设计: 在我校正门口所对的马路上,在学校东50m和西150m处分别有一个书店和一个超市,学校西100m和160m处分别有一个邮局和医院,分别用A、B、C、D表示书店、超市、邮局、医院,你会画图表示这一情境吗?(学生画图)
(二)合作交流,解读探究
师:对照大家画的图,为了使表达更清楚,我们把0左右两边的数分别用正数和负数来表示,即用一直线上的点把正数、负数、0都表示出来.也就是本节内容──数轴.
点拨 (1)引导学生学会画数轴.
第一步:画直线定原点
第二步:规定从原点向右的方向为正(左边为负方向)
第三步:选择适当的长度为单位长度(据情况而定)
拿出教学温度计,参照学生所画的数轴,观察温度计的结构和数轴的结构是否有共同之处.
对比思考:原点相当于什么;正方向与什么一致;单位长度又是什么?
(2)有了以上基础,我们可以来试着定义数轴:
规定了原点、正方向和单位长度的直线叫数轴.
做一做 学生自己练习画出数轴.
试一试:你能利用你自己画的数轴上的点来表示数4,1.5,-3,-,0吗?
讨论 若a是一个正数,则数轴上表示数a的点在原点的什么位置上?与原点相距多少个单位长度;表示-a的点在原点的什么位置上?与原点又相距了多少个长度单位?
小结 整数能在数轴上都找到点吗?分数呢?
(三)应用迁移,巩固提高
例1 下列所画数轴对不对?如果不对,指出错在哪里.
例2 试一试:用你画的数轴上的点表示4,1.5,-3,-,0
例3 如果a是一个正数,则数轴上表示数a的点在原点的什么位置上?表示-a的点在原点的什么位置上呢?
[提示] 由数轴上数的特点不准得到,正数都在原点的右边,负数都在原点左边.
[答案] 所有的有理数都可以在数轴上找个点与它对应,原点右边的点表示正数,原点左边的点表示负数.
[点评] 数与数轴上的点结合,这是一种重要的数学思想,数形结合.
例4 下列语句:①数轴上的点又能表示整数;②数轴是一条直线;③数轴上的一个点只能表示一个数;④数轴上找不到既不表示正数,又不表示负数的点;⑤数轴上的点所表示的数都是有理数.正确的说法有(B)
A.1个 B.2个 C.3个 D.4个
[提示]题中,结合数轴上的点与有理数的特点,可见①中错误的;②、③是正确的;④中可以含有0,⑤中应该是所有的有理数都可以在数轴上找出对应的点,但并不是数轴上的点都表示有理数.
例5 (1)与原点的距离为2.5个单位的点有 两 个,它们分别表示有理数 2.5 和 -2.5 .
(2)一个蜗牛从原点开始,先向左爬了4个单位,再向右爬了7个单位到达终点,那么终点表示的数是 +3 .
例6 在数轴上表示-2和1,并根据数轴指出所有大于-2而小于1的整数.
[点评] 本题反映了数形结合的思想方法.
例7 数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若这个数轴上随意画出一条长2000cm的线段AB,则线段AB盖住的整点是(C)
A.1998或1999 B.1999或2000
C.2000或2001 D.2001或2002
[点评] 本题体现了新课程标准的探索和实践能力.
(四)总结反思,拓展升华
数轴是非常重要的工具,它使数和直线上的点建立了对立关系.它揭示了数和形的内在联系,为我们今后进一步研究问题提供了新方法和新思想.大家要掌握数轴的三要素,正确画出数轴.提醒大家,所有的有理数都可以用数轴上的相关点来表示,但反过来并不成立,即数轴上的点并不都表示有理数.
一条直线的流水线上,依次有5个卡通人,它们站立的位置在数轴上依次用点M1、M2、M3、M4、M5表示,如图:
(1)点M4和M2所表示的有理数是什么?
(2)点M3和M5两点间的距离为多少?
(3)怎样将点M3移动,使它先达到M2,再达到M5,请用文字说明;
(4)若原点是一休息游乐所,那5个卡通人到游乐所休息的总路程为多少?
(五)课堂跟踪反馈
P11练习;P14习题2,3
§1.2.3相反数
[学情分析]在学完数轴之后,我们可以从数轴上直观的定义相反数的几何定义,这也是数形结合思想的初步应用。
[教学目标]
1、知识目标:①借助数轴了解相反数的概念,知道互为相反数的位置关系.
②给一个数,能求出它的相反数.
2、过程与方法目标:
①训练学生利用数轴应用数形结合的方法解决问题.
②培养学生自己归纳总结规律的能力.
3、知识与情感目标:
①通过相反数的学习,渗透数形结合的思想.
②感受事物之间对立、统一联系的辩证思想.
[教学重难点]
重点:理解相反数的意义.
难点:理解和掌握双重符号简化的规律.
[教与学互动设计]
(一)创设情境,导入新课
活动 请一个学生到讲台前面对大家,向前走5步,向后走5步.
交流 如果向前走为正,那向前走5步与向后走5步分别记作什么?
(二)合作交流,解读探究
1.观察下列数:6和-6,2和-2,7和-7,和-,并把它们在数轴上标出.
想一想 (1)上述各对数之间有什么特点?
(2)表示这两对数的点在数轴上有什么特点?
(3)你能够写出具有上述特点的数吗?
观察 像这样只有符号不同的两个数叫相反数.
两个互为相反数的数,在数轴上的对应点(0除外),是在原点两旁,并且距离原点相等的两个点.即:互为相反数的两个数在数轴上的对应点关于原点对称.我们把a的相反数记为-a,并且规定0的相反数就是零.
[总结]1.在正数前面添上一个“-”号,就得到这个正数的相反数,是一个负数;把负数前的“-”号去掉,就得到这个负数的相反数,是一个正数.
2.在任意一个数前面添上“-”号,新的数就是原数的相反数.如-(+5)=-5,表示+5的相反数为-5;-(-5)=5,表示-5的相反数是5;-0=0,表示0的相反数是0.
(三)应用迁移,巩固提高
例1 填空
(1)-5.8是 5.8 的相反数, 3 的相反数是-(+3),a的相反数是 –a ,a-b的相反数是 -(a-b) ,0的相反数是 0 .
(2)正数的相反数是 负数 ,负数的相反数是 正数 , 0 的相反数是它本身.
例2 下列判断不正确的有 (C)
①互为相反数的两个数一定不相等;②互为相反数的数在数轴上的点一定在原点的两边;③所有的有理数都有相反数;④相反数是符号相反的两个点.
A.1个 B.2个 C.3个 D.4个
例3 化简下列各符号:
(1)-[-(-2)] (2)+{-[-(+5)]}
(3)-{-{-…-(-6)}…}(共n个负号)
[提示] 化简的规律是:有偶数个负号,结果为正;有奇数个负号,结果为负.
例4 数轴上A点表示+4,B、C两点所表示的数是互为相反数,且C到A的距离为2,点B和点C各对应什么数?
[提示] 画出数轴,结合数轴的特点来分析.
[点评] 经历观察数学活动,发展自己的指导能力.
(四)总结反思,拓展升华
归纳 ①相反数的概念及表示方法.
②相反数的代数意义和几何意义.
③符号的化简.
1.(1)王亮说:“一个数总比它的相反数大”.你认为正确吗?为什么?
(2)若数轴上表示一对相反数的两点之间的距离为26.8,求这两个数.
2.你若a是不小于-1又不大于3的数,那么a的相反数是什么样的数呢?
[点评] 在解决问题中,能进行简单的、有条理的思考.
(五)课堂跟踪反馈
P11练习:1,2,3;P15.3
§1.2.4绝对值
[教学目标]
知识目标:
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
2、过程与方法目标:
经历绝对值的代数定义转化成数学式子的过程中,培养学生运用数学转化思想指导思维活动的能力
3、知识与情感目标:
①通过解释绝对值的几何意义,渗透数形结合的思想.
②体验运用直观知识解决数学问题的成功.
[教学重难点]
重点:给出一个数,会求它的绝对值.
难点:绝对值的几何意义、代数定义的导出.
[教与学互动设计]
(一)创设情境,导入新课
活动 请两同学到讲台前,分别向左、向右行3米.
交流 ①他们所走的路线相同吗? ②若向右为正,分别可怎样表示他们的位置? ③他们所走的路程的远近是多少?
(二)合作交流,解读探究
观察 出示一组数6与-6,3.5与-3.5,1和-1,它们是一对互为________,它们的__________不同,__________相同.
[总结] 例如6和-6两个数在数轴上的两点虽然分布在原点的两边,但它们到原点的距离相等,如果我们不考虑两点在原点的哪一边,只考虑它们离开原点的距离,这个距离都是6,我们就把这个距离叫做6和-6的绝对值.
绝对值:在数轴上表示数a的点与原点的距离叫做a的绝对值,记作│a│.
想一想 (1)-3的绝对值是什么? (2)+2的绝对值是多少?
(3)-12的绝对值呢? (4)a的绝对值呢?
交流 同桌间合作交流,每位同学任说五个数,由同桌指出它们的绝对值.
思考 例1 求8,-8,3,-3,,-的绝对值.(出示胶片)
由此,你想到什么规律?
总结 1.互为相反数的两个数的绝对值相同.
2.正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是零.
讨论 字母a可以代表任意的数,那么表示什么数?这时a的绝对值分别是多少?
学生活动:分组讨论,教师加入讨论,学生相反补充回答.
归纳 若a>0,则│a│=a
若a<0,则│a│=-a
若a=0,则│a│=0
(三)应用迁移,巩固提高
例题填空:
(1)绝对值等于4的数有 2 个,它们是 ±4 .
(2)绝对值等于-3的数有 0 个.
(3)绝对值等于本身的数有 无数 个,它们是 0和正数(非负数) .
(4)①若│a│=2,则a= ±2 .
②若│-a│=3,则a= ±3 .
(5)绝对值不大于2的整数是 0,±1,±2 .
[点评]去绝对值符号,首先要判断绝对值里的正负情况,由此发展自身的合情推理能力.
(四)总结反思,拓展升华
本节课,我们学习认识了绝对值,要注意掌握以下两点:①一个数的绝对值是在数轴上表示这个数的点到原点的距离;②求一个数的绝对值必须先判断是正数还是负数.
(五)课堂跟踪反馈
P12练习; P15.习题4
§1.2.5有理数的大小比较
[学情分析]学生在学习了数轴之后,可以直观地从数轴上点的位置来判断两个数的大小。在学习了绝对值之后,又可以利用绝对值的特点来比较两个数的大小,尤其是两个负数的大小。可借此向学生展示数学方法的多样性。
[教学目标]
1.知识与技能
会利用绝对值比较两个负数的大小.
2.过程与方法
利用绝对值概念比较有理数的大小,培养学生的逻辑思维能力.
3.情感、态度与价值观
敢于面对数学活动中的困难,有学好数学的自信心.
[教学重,难点]
重点:利用绝对值比较两个负数的大小.
难点:利用绝对值比较两个异分母负分数的大小.
[教与学互动设计]
(一)创设情境,导入新课
投影 你能比较下列各组数的大小吗?
(1)│-3│与│-8│ (2)4与-5 (3)0与3
(4)-7和0 (5)0.9和1.2
(二)合作交流,解读探究
讨论交流 由以上各组数的大小比较可见:正数都大于0,0都大于负数,正数都大于负数.
思考 若任取两个负数,该如何比较它的大小呢?
点拨 若-7表示-7℃,-1表示-1℃,则两个温度谁高谁低?
[总结] 两个负数,绝对值大的反而小,或说,两个负数绝对值小的反而大.
注意 ①比较两个负数的大小又多了一种方法,即:两个负数,绝对值大的反而小.
②异号的两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑先比较它们的绝对值.
③在数轴上表示有理数,它们从左到右的顺序也就是从小到大的顺序,即:左边的数总比右边的数要小.即:利用数轴来比较有理数的大小.
(三)应用迁移,巩固提高
例1 比较下列各组数的大小
(1)-和-2.7
(2)-和-
例2 按从大到小的顺序,用“〈”号把下列数连接起来.
-4,-(-),│-0.6│,-0.6,-│4.2│
自己任写三个数,使它大于-而小于-.
[点评] 此题是一个开放型问题,培养学生发散性思维.
例4 已知│a│=4,│b│=3,且a>b,求a、b的值.
(四)总结反思,拓展升华
1.本节课所学的有理数的大小比较你能掌握两种方法吗?
(1)利用数轴,在数轴上把这些数表示出来,然后根据“数轴上左边的数总比右边的数大”来比较;
(2)利用比较法则:“正数大于零,负数小于零,两个负数,绝对值大的反而小”来进行.
2.(1)阅读下列比较-a与-a的大小的解题过程:
解:∵│-a│=a,│-a│=a
又∵a>a ∴-a<-a
你认为上述解答过程正确吗?与同学们研究,并发表你的看法.
(五)课堂跟踪反馈 P14.练习 P15,习题5
…
…
…
…
§1.2.1有理数;
[学情分析]有理数是学生在学习了自然数和小数等的概念上的一次扩展,它不仅是整个中学学生学习的基础,而且也是学生在日常生活中最常见的数学概念。
[教学目标]
1.知识与技能
①理解有理数的意义.
②能把给出的有理数按要求分类.
③了解0在有理数分类的作用.
2.过程与方法
经历本节的学习,培养学生树立分类讨论的观点和能正确地进行分类的能力.
3.情感、态度与价值观
通过联系与发展、对立与统一的思考方法对学生进行辩证唯物主义教育.
[教学重点]理解有理数的概念。
[教学难点]掌握有理数的两种分类.
[教学策略]由于有理数的概念较易被学生理解,而前一段的教学内容刚刚引进了负数的概念,因此可以把这部分的内容提前到学完负数之后。并可以向学生展示数的扩展示意图:
[教与学互动设计]
(一)创设情境,导入新课
接球游戏:在游戏过程中,发现数字不够用了,引出负数概念
(二)合作交流,解读探究
学生列举,如:3,5.7,-7,-9,-10,0,,,-3, -7.4,5.2…
议一议 你能说说这些数的特点吗?
学生回答,并相互补充:有小学学过的整数、0、分数,也有负整数、负分数.
说明:我们把所有的这些数统称为有理数.
试一试 你能对以上各种类型的数作出一张分类表吗?
有理数
说明:以上分类,若学生思考有困难,可加以引导:因为整数和分数统称为有理数,所以有理数可分为整数和分数两大类,那么整数又包含那些数?分数呢?
做一做 以上按整数和分数来分,那可不可以按性质(正数、负数)来分呢,试一试.
有理数
(3)数的集合
把所有正数组成的集合,叫做正数集合.
试一试 试着归纳总结,什么是负数集合、整数集合、分数集合、有理数集合.
(三)应用迁移,巩固提高
例1 把下列各数填入相应的集合内:
,3.1416,0,2004,-,-0.23456,10%,10.l,0.67,-89
正数集合 负数集合 整数集合 分数集合
例2 以下是两位同学的分类方法,你认为他们的分类的结果正确吗?为什么?
有理数 有理数
[点评] 以上是对各类有理数的特点及有理数的分类进行的训练,基础性强,需要重视
例3下列说法正确的是(B)
①0是最小的正整数 ②0是最小的有理数
③0不是负数 ④0既是非正数,也是非负数
A.1个 B.2个 C.3个 D.4个
例4 如果用字母表示一个数,那a可能是什么样的数,一定为正数吗?与你的伙伴交流一下你的看法.
[点评] 此题开放性较强.同时,要求学生能用分类的思想对a全面认识.
(四)总结反思,拓展升华
提问:今天你获得了哪些知识?
由学生自己小结,然后教师总结:今天我们学习了有理数的定义和两种分类的方法.我们要能正确地判断一个数属于哪一类,要特别注意“0”的正确说法.
请你在图1-2-1的圈中填上适合的数,使得圈内的数依次为整数集、有理数集、正数集、分数集、负数集.
2.有理数按正、负可分为
按数的类型分,可分为
(1)你能自己再制定一个标准,对有理数进行另一种分类吗?
(2)生活中,我们也常常对事物进行分类,请你举例说明.
3.下面两个圈分别表示负数集和分数集,你能说出两个图的重叠部分表示什么数的集合呢?
(五)课堂跟踪反馈
P8.练习 P14.习题1.2 第1题
§1.2.2数轴:
[学情分析]数轴概念是数形结合的基础,是帮助学生理解数学、学好数学的重要思想方法。,本节后面的相反数等的概念和运算都是结合数轴进行的,由此可见学生学好数轴概念的重要性。数轴是用“长度”度量各类量的抽象,日常生活中常见的用温度计度量温度,用弹簧称(刻度在直线上)称重量等,都已为学生学习数轴概念打下了基础。在教学中,数轴的三要素都要将认真分析它的作用,使学生从直观认识上升到理性认识。
[教学目标]
1、知识目标:①掌握数轴三要素,能正确画出数轴.
②能将已知数在数轴上表示出来,能说出数轴上已知点所表示的数.
2、过程与方法目标:
①使学生受到把实际问题抽象成数学问题的训练,逐步形成应用数学的意识.
②结合本节内容,对学生渗透数形结合的重要思想方法.
3.情感与能力目标:
使学生进一步形成数学来源于实践,反过来又服务于实践的辩证唯物主义观点.
[教学重难点]
重点:数轴的概念.
难点:从直观认识到理性认识,从而建立数轴概念.
[教与学互动设计]
(一)创设情境,导入新课
情景设计: 在我校正门口所对的马路上,在学校东50m和西150m处分别有一个书店和一个超市,学校西100m和160m处分别有一个邮局和医院,分别用A、B、C、D表示书店、超市、邮局、医院,你会画图表示这一情境吗?(学生画图)
(二)合作交流,解读探究
师:对照大家画的图,为了使表达更清楚,我们把0左右两边的数分别用正数和负数来表示,即用一直线上的点把正数、负数、0都表示出来.也就是本节内容──数轴.
点拨 (1)引导学生学会画数轴.
第一步:画直线定原点
第二步:规定从原点向右的方向为正(左边为负方向)
第三步:选择适当的长度为单位长度(据情况而定)
拿出教学温度计,参照学生所画的数轴,观察温度计的结构和数轴的结构是否有共同之处.
对比思考:原点相当于什么;正方向与什么一致;单位长度又是什么?
(2)有了以上基础,我们可以来试着定义数轴:
规定了原点、正方向和单位长度的直线叫数轴.
做一做 学生自己练习画出数轴.
试一试:你能利用你自己画的数轴上的点来表示数4,1.5,-3,-,0吗?
讨论 若a是一个正数,则数轴上表示数a的点在原点的什么位置上?与原点相距多少个单位长度;表示-a的点在原点的什么位置上?与原点又相距了多少个长度单位?
小结 整数能在数轴上都找到点吗?分数呢?
(三)应用迁移,巩固提高
例1 下列所画数轴对不对?如果不对,指出错在哪里.
例2 试一试:用你画的数轴上的点表示4,1.5,-3,-,0
例3 如果a是一个正数,则数轴上表示数a的点在原点的什么位置上?表示-a的点在原点的什么位置上呢?
[提示] 由数轴上数的特点不准得到,正数都在原点的右边,负数都在原点左边.
[答案] 所有的有理数都可以在数轴上找个点与它对应,原点右边的点表示正数,原点左边的点表示负数.
[点评] 数与数轴上的点结合,这是一种重要的数学思想,数形结合.
例4 下列语句:①数轴上的点又能表示整数;②数轴是一条直线;③数轴上的一个点只能表示一个数;④数轴上找不到既不表示正数,又不表示负数的点;⑤数轴上的点所表示的数都是有理数.正确的说法有(B)
A.1个 B.2个 C.3个 D.4个
[提示]题中,结合数轴上的点与有理数的特点,可见①中错误的;②、③是正确的;④中可以含有0,⑤中应该是所有的有理数都可以在数轴上找出对应的点,但并不是数轴上的点都表示有理数.
例5 (1)与原点的距离为2.5个单位的点有 两 个,它们分别表示有理数 2.5 和 -2.5 .
(2)一个蜗牛从原点开始,先向左爬了4个单位,再向右爬了7个单位到达终点,那么终点表示的数是 +3 .
例6 在数轴上表示-2和1,并根据数轴指出所有大于-2而小于1的整数.
[点评] 本题反映了数形结合的思想方法.
例7 数轴上表示整数的点称为整点,某数轴的单位长度是1cm,若这个数轴上随意画出一条长2000cm的线段AB,则线段AB盖住的整点是(C)
A.1998或1999 B.1999或2000
C.2000或2001 D.2001或2002
[点评] 本题体现了新课程标准的探索和实践能力.
(四)总结反思,拓展升华
数轴是非常重要的工具,它使数和直线上的点建立了对立关系.它揭示了数和形的内在联系,为我们今后进一步研究问题提供了新方法和新思想.大家要掌握数轴的三要素,正确画出数轴.提醒大家,所有的有理数都可以用数轴上的相关点来表示,但反过来并不成立,即数轴上的点并不都表示有理数.
一条直线的流水线上,依次有5个卡通人,它们站立的位置在数轴上依次用点M1、M2、M3、M4、M5表示,如图:
(1)点M4和M2所表示的有理数是什么?
(2)点M3和M5两点间的距离为多少?
(3)怎样将点M3移动,使它先达到M2,再达到M5,请用文字说明;
(4)若原点是一休息游乐所,那5个卡通人到游乐所休息的总路程为多少?
(五)课堂跟踪反馈
P11练习;P14习题2,3
§1.2.3相反数
[学情分析]在学完数轴之后,我们可以从数轴上直观的定义相反数的几何定义,这也是数形结合思想的初步应用。
[教学目标]
1、知识目标:①借助数轴了解相反数的概念,知道互为相反数的位置关系.
②给一个数,能求出它的相反数.
2、过程与方法目标:
①训练学生利用数轴应用数形结合的方法解决问题.
②培养学生自己归纳总结规律的能力.
3、知识与情感目标:
①通过相反数的学习,渗透数形结合的思想.
②感受事物之间对立、统一联系的辩证思想.
[教学重难点]
重点:理解相反数的意义.
难点:理解和掌握双重符号简化的规律.
[教与学互动设计]
(一)创设情境,导入新课
活动 请一个学生到讲台前面对大家,向前走5步,向后走5步.
交流 如果向前走为正,那向前走5步与向后走5步分别记作什么?
(二)合作交流,解读探究
1.观察下列数:6和-6,2和-2,7和-7,和-,并把它们在数轴上标出.
想一想 (1)上述各对数之间有什么特点?
(2)表示这两对数的点在数轴上有什么特点?
(3)你能够写出具有上述特点的数吗?
观察 像这样只有符号不同的两个数叫相反数.
两个互为相反数的数,在数轴上的对应点(0除外),是在原点两旁,并且距离原点相等的两个点.即:互为相反数的两个数在数轴上的对应点关于原点对称.我们把a的相反数记为-a,并且规定0的相反数就是零.
[总结]1.在正数前面添上一个“-”号,就得到这个正数的相反数,是一个负数;把负数前的“-”号去掉,就得到这个负数的相反数,是一个正数.
2.在任意一个数前面添上“-”号,新的数就是原数的相反数.如-(+5)=-5,表示+5的相反数为-5;-(-5)=5,表示-5的相反数是5;-0=0,表示0的相反数是0.
(三)应用迁移,巩固提高
例1 填空
(1)-5.8是 5.8 的相反数, 3 的相反数是-(+3),a的相反数是 –a ,a-b的相反数是 -(a-b) ,0的相反数是 0 .
(2)正数的相反数是 负数 ,负数的相反数是 正数 , 0 的相反数是它本身.
例2 下列判断不正确的有 (C)
①互为相反数的两个数一定不相等;②互为相反数的数在数轴上的点一定在原点的两边;③所有的有理数都有相反数;④相反数是符号相反的两个点.
A.1个 B.2个 C.3个 D.4个
例3 化简下列各符号:
(1)-[-(-2)] (2)+{-[-(+5)]}
(3)-{-{-…-(-6)}…}(共n个负号)
[提示] 化简的规律是:有偶数个负号,结果为正;有奇数个负号,结果为负.
例4 数轴上A点表示+4,B、C两点所表示的数是互为相反数,且C到A的距离为2,点B和点C各对应什么数?
[提示] 画出数轴,结合数轴的特点来分析.
[点评] 经历观察数学活动,发展自己的指导能力.
(四)总结反思,拓展升华
归纳 ①相反数的概念及表示方法.
②相反数的代数意义和几何意义.
③符号的化简.
1.(1)王亮说:“一个数总比它的相反数大”.你认为正确吗?为什么?
(2)若数轴上表示一对相反数的两点之间的距离为26.8,求这两个数.
2.你若a是不小于-1又不大于3的数,那么a的相反数是什么样的数呢?
[点评] 在解决问题中,能进行简单的、有条理的思考.
(五)课堂跟踪反馈
P11练习:1,2,3;P15.3
§1.2.4绝对值
[教学目标]
知识目标:
①能根据一个数的绝对值表示“距离”,初步理解绝对值的概念,能求一个数的绝对值.
②通过应用绝对值解决实际问题,体会绝对值的意义和作用.
2、过程与方法目标:
经历绝对值的代数定义转化成数学式子的过程中,培养学生运用数学转化思想指导思维活动的能力
3、知识与情感目标:
①通过解释绝对值的几何意义,渗透数形结合的思想.
②体验运用直观知识解决数学问题的成功.
[教学重难点]
重点:给出一个数,会求它的绝对值.
难点:绝对值的几何意义、代数定义的导出.
[教与学互动设计]
(一)创设情境,导入新课
活动 请两同学到讲台前,分别向左、向右行3米.
交流 ①他们所走的路线相同吗? ②若向右为正,分别可怎样表示他们的位置? ③他们所走的路程的远近是多少?
(二)合作交流,解读探究
观察 出示一组数6与-6,3.5与-3.5,1和-1,它们是一对互为________,它们的__________不同,__________相同.
[总结] 例如6和-6两个数在数轴上的两点虽然分布在原点的两边,但它们到原点的距离相等,如果我们不考虑两点在原点的哪一边,只考虑它们离开原点的距离,这个距离都是6,我们就把这个距离叫做6和-6的绝对值.
绝对值:在数轴上表示数a的点与原点的距离叫做a的绝对值,记作│a│.
想一想 (1)-3的绝对值是什么? (2)+2的绝对值是多少?
(3)-12的绝对值呢? (4)a的绝对值呢?
交流 同桌间合作交流,每位同学任说五个数,由同桌指出它们的绝对值.
思考 例1 求8,-8,3,-3,,-的绝对值.(出示胶片)
由此,你想到什么规律?
总结 1.互为相反数的两个数的绝对值相同.
2.正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是零.
讨论 字母a可以代表任意的数,那么表示什么数?这时a的绝对值分别是多少?
学生活动:分组讨论,教师加入讨论,学生相反补充回答.
归纳 若a>0,则│a│=a
若a<0,则│a│=-a
若a=0,则│a│=0
(三)应用迁移,巩固提高
例题填空:
(1)绝对值等于4的数有 2 个,它们是 ±4 .
(2)绝对值等于-3的数有 0 个.
(3)绝对值等于本身的数有 无数 个,它们是 0和正数(非负数) .
(4)①若│a│=2,则a= ±2 .
②若│-a│=3,则a= ±3 .
(5)绝对值不大于2的整数是 0,±1,±2 .
[点评]去绝对值符号,首先要判断绝对值里的正负情况,由此发展自身的合情推理能力.
(四)总结反思,拓展升华
本节课,我们学习认识了绝对值,要注意掌握以下两点:①一个数的绝对值是在数轴上表示这个数的点到原点的距离;②求一个数的绝对值必须先判断是正数还是负数.
(五)课堂跟踪反馈
P12练习; P15.习题4
§1.2.5有理数的大小比较
[学情分析]学生在学习了数轴之后,可以直观地从数轴上点的位置来判断两个数的大小。在学习了绝对值之后,又可以利用绝对值的特点来比较两个数的大小,尤其是两个负数的大小。可借此向学生展示数学方法的多样性。
[教学目标]
1.知识与技能
会利用绝对值比较两个负数的大小.
2.过程与方法
利用绝对值概念比较有理数的大小,培养学生的逻辑思维能力.
3.情感、态度与价值观
敢于面对数学活动中的困难,有学好数学的自信心.
[教学重,难点]
重点:利用绝对值比较两个负数的大小.
难点:利用绝对值比较两个异分母负分数的大小.
[教与学互动设计]
(一)创设情境,导入新课
投影 你能比较下列各组数的大小吗?
(1)│-3│与│-8│ (2)4与-5 (3)0与3
(4)-7和0 (5)0.9和1.2
(二)合作交流,解读探究
讨论交流 由以上各组数的大小比较可见:正数都大于0,0都大于负数,正数都大于负数.
思考 若任取两个负数,该如何比较它的大小呢?
点拨 若-7表示-7℃,-1表示-1℃,则两个温度谁高谁低?
[总结] 两个负数,绝对值大的反而小,或说,两个负数绝对值小的反而大.
注意 ①比较两个负数的大小又多了一种方法,即:两个负数,绝对值大的反而小.
②异号的两数比较大小,要考虑它们的正负;同号两数比较大小,要考虑先比较它们的绝对值.
③在数轴上表示有理数,它们从左到右的顺序也就是从小到大的顺序,即:左边的数总比右边的数要小.即:利用数轴来比较有理数的大小.
(三)应用迁移,巩固提高
例1 比较下列各组数的大小
(1)-和-2.7
(2)-和-
例2 按从大到小的顺序,用“〈”号把下列数连接起来.
-4,-(-),│-0.6│,-0.6,-│4.2│
自己任写三个数,使它大于-而小于-.
[点评] 此题是一个开放型问题,培养学生发散性思维.
例4 已知│a│=4,│b│=3,且a>b,求a、b的值.
(四)总结反思,拓展升华
1.本节课所学的有理数的大小比较你能掌握两种方法吗?
(1)利用数轴,在数轴上把这些数表示出来,然后根据“数轴上左边的数总比右边的数大”来比较;
(2)利用比较法则:“正数大于零,负数小于零,两个负数,绝对值大的反而小”来进行.
2.(1)阅读下列比较-a与-a的大小的解题过程:
解:∵│-a│=a,│-a│=a
又∵a>a ∴-a<-a
你认为上述解答过程正确吗?与同学们研究,并发表你的看法.
(五)课堂跟踪反馈 P14.练习 P15,习题5
…
…
…
…
