江苏省百师联盟2020-2021学年高三下学期3月摸底联考数学试卷(word版含答案)
文档属性
| 名称 | 江苏省百师联盟2020-2021学年高三下学期3月摸底联考数学试卷(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 00:00:00 | ||
图片预览




文档简介
2021届高三百师联盟3月摸底联考数学试卷
2021.3
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合M=,N=,则集合MN=
A.
B.
C.
D.
2.复数z满足:,=
A.
B.
C.
D.
3.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止2020年10月10日,我国共进行了六次人口普查,右图是这次人口普查的人数和增幅情况,下列说法正确的是
A.人口数逐次增加,第二次增幅最大
B.第六次普查人数最多,第四次增幅最小
C.第六次普查人数最多,第三次增幅最大
D.人口数逐次增加,从第二次开始增幅减小
4.已知圆C:x2+y2﹣4x﹣2y+3=0,过原点的直线l与圆C相交于A,B两点,则当△ABC的面积最大时,直线l的方程为
A.或
B.或
C.或
D.
5.将3名男生1名女生分配到甲、乙、丙三个社区参加社会实践,每个社区至少一名同学,则恰好一名女生和一名男生分到甲社区的概率是
A.
B.
C.
D.
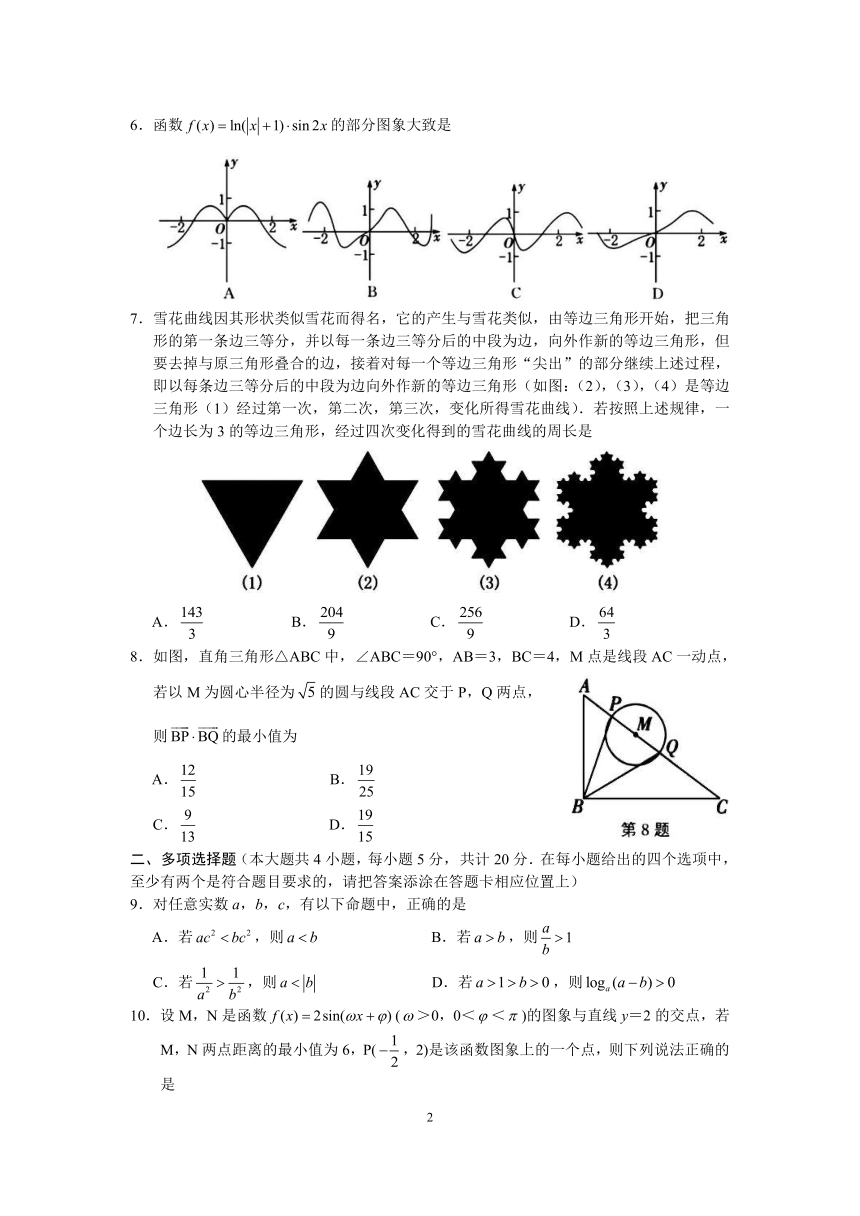
6.函数的部分图象大致是
7.雪花曲线因其形状类似雪花而得名,它的产生与雪花类似,由等边三角形开始,把三角形的第一条边三等分,并以每一条边三等分后的中段为边,向外作新的等边三角形,但要去掉与原三角形叠合的边,接着对每一个等边三角形“尖出”的部分继续上述过程,即以每条边三等分后的中段为边向外作新的等边三角形(如图:(2),(3),(4)是等边三角形(1)经过第一次,第二次,第三次,变化所得雪花曲线).若按照上述规律,一个边长为3的等边三角形,经过四次变化得到的雪花曲线的周长是
A.
B.
C.
D.
8.如图,直角三角形△ABC中,∠ABC=90°,AB=3,BC=4,M点是线段AC一动点,若以M为圆心半径为的圆与线段AC交于P,Q两点,
则的最小值为
A.
B.
C.
D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.对任意实数a,b,c,有以下命题中,正确的是
A.若,则
B.若,则
C.若,则
D.若,则
10.设M,N是函数(>0,0<<)的图象与直线y=2的交点,若M,N两点距离的最小值为6,P(,2)是该函数图象上的一个点,则下列说法正确的是
A.该函数图象的一个对称中心是(7,0)
B.该函数图象的对称轴方程是,kZ
C.在[,]上单调递增
D.
11.如图所示,在棱长为1的正方体ABCD—A1B1C1D1中,M,N分别为棱A1D1,DD1的中点,则以下四个结论正确的是
A.B1C∥MN
B.B1C⊥平面MNC1
C.A到直线MN的距离为
D.过MN作该正方体外接球的截面,所得截面的面积的
最小值为
12.已知函数在区间(1,e)内有唯一零点,则m的可能取值为
A.
B.
C.
D.
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.若,则=
.
14.若的展开式中的系数为160,则a=
.
15.函数是定义在R上的函数,且,为的导函数,且>0,则不等式的解集是
.
16.过抛物线C:x2=2py上点M作抛物线D:y2=4x的两条切线l1,l2,切点分别为P,Q,若△MPQ的重心为G(1,),则p=
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在①,;②;③这三个条件中任选一个,补充在下面问题中,并作答:
(1)求的通项公式;
(2)求的前n项和.
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分12分)
已知a,b,c是△ABC的内角A,B,C的对边,且5cosBcosC+2=5sinBsinC+cos2A.
(1)求角A的大小;
(2)若△ABC的面积S=,c=,求sinBsinC的值.
19.(本小题满分12分)
如图,在直角△ABC中,直角边AC=2,∠A=60°,M为AB的中点,Q为BC的中点,将三角形△AMC沿着MC折起,使A1M⊥MB,(A1为A翻折后所在的点),连接MQ.
(1)求证:MQ⊥AB;
(2)求直线MB与面A1MC所成角的正弦值.
20.(本小题满分12分)
近年来,我国的电子商务行业发展迅速,与此同时,相关管理部门建立了针对电商的商品和服务评价系统.现从评价系统中选出200次成功的交易,并对其评价进行统计,对商品的好评率为,对服务的好评率为,其中对商品和服务均为好评的有80次.
(1)是否可以在犯错误概率不超过0.1的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的4次购物中,设对商品和服务全好评的次数为随机变量X,求对商品和服务全好评的次数X的分布列及其期望.
参考公式:独立性检验统计量,其中.
临界值表:
P()
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
21.(本小题满分12分)
已知椭圆C:(a>b>0)的上、下顶点分别为A,B,P为直线y=2上的动点,当点P位于点(1,2)时,△ABP的面积S△ABP=1,椭圆C上任意一点到椭圆的左焦点F的最短距离为.
(1)求椭圆C的方程;
(2)连接PA,PB,直线PA,PB分别交椭圆于M、N(异于点A,B)两点,证明:直线MN过定点.
22.(本小题满分12分)
已知函数,x[0,].
(1)证明:当a=﹣1时,函数有唯一的极大值点;
(2)当﹣2<a<0时,证明:.
参考答案
1.B
2.A
3.C
4.A
5.D
6.B
7.C
8.B
9.AC
10.ABD
11.ACD
12.BC
13.或3
14.2
15.(,1)(2,)
16.
17.
18.
19.
20.
21.
22.
2
2021.3
一、单项选择题(本大题共8小题,每小题5分,共计40分.在每小题给出的四个选项中,只有一个是符合题目要求的,请把答案添涂在答题卡相应位置上)
1.已知集合M=,N=,则集合MN=
A.
B.
C.
D.
2.复数z满足:,=
A.
B.
C.
D.
3.人口普查是世界各国所广泛采用的搜集人口资料的一种科学方法,是提供全国基本人口数据的主要来源.根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作,人口普查资料是制定人口政策的依据和前提.截止2020年10月10日,我国共进行了六次人口普查,右图是这次人口普查的人数和增幅情况,下列说法正确的是
A.人口数逐次增加,第二次增幅最大
B.第六次普查人数最多,第四次增幅最小
C.第六次普查人数最多,第三次增幅最大
D.人口数逐次增加,从第二次开始增幅减小
4.已知圆C:x2+y2﹣4x﹣2y+3=0,过原点的直线l与圆C相交于A,B两点,则当△ABC的面积最大时,直线l的方程为
A.或
B.或
C.或
D.
5.将3名男生1名女生分配到甲、乙、丙三个社区参加社会实践,每个社区至少一名同学,则恰好一名女生和一名男生分到甲社区的概率是
A.
B.
C.
D.
6.函数的部分图象大致是
7.雪花曲线因其形状类似雪花而得名,它的产生与雪花类似,由等边三角形开始,把三角形的第一条边三等分,并以每一条边三等分后的中段为边,向外作新的等边三角形,但要去掉与原三角形叠合的边,接着对每一个等边三角形“尖出”的部分继续上述过程,即以每条边三等分后的中段为边向外作新的等边三角形(如图:(2),(3),(4)是等边三角形(1)经过第一次,第二次,第三次,变化所得雪花曲线).若按照上述规律,一个边长为3的等边三角形,经过四次变化得到的雪花曲线的周长是
A.
B.
C.
D.
8.如图,直角三角形△ABC中,∠ABC=90°,AB=3,BC=4,M点是线段AC一动点,若以M为圆心半径为的圆与线段AC交于P,Q两点,
则的最小值为
A.
B.
C.
D.
二、?多项选择题(本大题共4小题,每小题5分,?共计20分.在每小题给出的四个选项中,至少有两个是符合题目要求的,请把答案添涂在答题卡相应位置上)
9.对任意实数a,b,c,有以下命题中,正确的是
A.若,则
B.若,则
C.若,则
D.若,则
10.设M,N是函数(>0,0<<)的图象与直线y=2的交点,若M,N两点距离的最小值为6,P(,2)是该函数图象上的一个点,则下列说法正确的是
A.该函数图象的一个对称中心是(7,0)
B.该函数图象的对称轴方程是,kZ
C.在[,]上单调递增
D.
11.如图所示,在棱长为1的正方体ABCD—A1B1C1D1中,M,N分别为棱A1D1,DD1的中点,则以下四个结论正确的是
A.B1C∥MN
B.B1C⊥平面MNC1
C.A到直线MN的距离为
D.过MN作该正方体外接球的截面,所得截面的面积的
最小值为
12.已知函数在区间(1,e)内有唯一零点,则m的可能取值为
A.
B.
C.
D.
三、填空题(本大题共4小题,?每小题5分,共计20分.请把答案填写在答题卡相应位置上)
13.若,则=
.
14.若的展开式中的系数为160,则a=
.
15.函数是定义在R上的函数,且,为的导函数,且>0,则不等式的解集是
.
16.过抛物线C:x2=2py上点M作抛物线D:y2=4x的两条切线l1,l2,切点分别为P,Q,若△MPQ的重心为G(1,),则p=
.
四、解答题(本大题共6小题,共计70分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)
在①,;②;③这三个条件中任选一个,补充在下面问题中,并作答:
(1)求的通项公式;
(2)求的前n项和.
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分12分)
已知a,b,c是△ABC的内角A,B,C的对边,且5cosBcosC+2=5sinBsinC+cos2A.
(1)求角A的大小;
(2)若△ABC的面积S=,c=,求sinBsinC的值.
19.(本小题满分12分)
如图,在直角△ABC中,直角边AC=2,∠A=60°,M为AB的中点,Q为BC的中点,将三角形△AMC沿着MC折起,使A1M⊥MB,(A1为A翻折后所在的点),连接MQ.
(1)求证:MQ⊥AB;
(2)求直线MB与面A1MC所成角的正弦值.
20.(本小题满分12分)
近年来,我国的电子商务行业发展迅速,与此同时,相关管理部门建立了针对电商的商品和服务评价系统.现从评价系统中选出200次成功的交易,并对其评价进行统计,对商品的好评率为,对服务的好评率为,其中对商品和服务均为好评的有80次.
(1)是否可以在犯错误概率不超过0.1的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的4次购物中,设对商品和服务全好评的次数为随机变量X,求对商品和服务全好评的次数X的分布列及其期望.
参考公式:独立性检验统计量,其中.
临界值表:
P()
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
21.(本小题满分12分)
已知椭圆C:(a>b>0)的上、下顶点分别为A,B,P为直线y=2上的动点,当点P位于点(1,2)时,△ABP的面积S△ABP=1,椭圆C上任意一点到椭圆的左焦点F的最短距离为.
(1)求椭圆C的方程;
(2)连接PA,PB,直线PA,PB分别交椭圆于M、N(异于点A,B)两点,证明:直线MN过定点.
22.(本小题满分12分)
已知函数,x[0,].
(1)证明:当a=﹣1时,函数有唯一的极大值点;
(2)当﹣2<a<0时,证明:.
参考答案
1.B
2.A
3.C
4.A
5.D
6.B
7.C
8.B
9.AC
10.ABD
11.ACD
12.BC
13.或3
14.2
15.(,1)(2,)
16.
17.
18.
19.
20.
21.
22.
2
同课章节目录
