5.4数列的应用-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析
文档属性
| 名称 | 5.4数列的应用-【新教材】2020-2021学年人教B版(2019)高中数学选择性必修第三册课时练习Word含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 465.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-09 22:24:48 | ||
图片预览



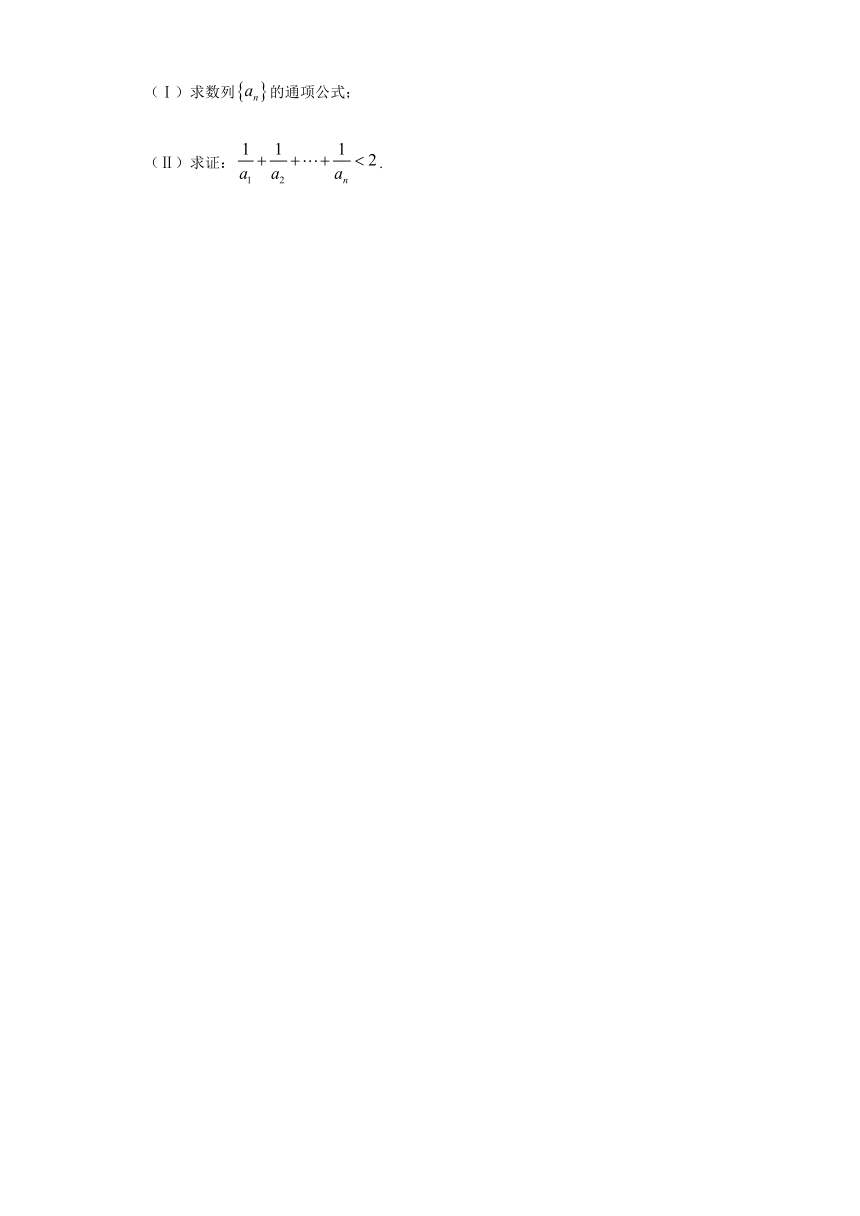

文档简介
5.4数列的应用课时作业
A级 巩固基础
一、单选题
1.按活期存入银行1000元,年利率是0.52%,那么按照单利,第5年末的本利和是( )
A.1036元 B.1028元 C.1043元 D.1026元
2.一批设备价值万元,由于使用磨损,每年比上一年价值降低,则年后这批设备的价值为( )
A. B. C. D.
3.2019年我国国内生产总值增长率为6.1%,达到了990865亿元,实现了新的跨越,2020年我们将全面建成小康社会,实现第一个一百年的奋斗目标.如果从2020年初开始,以后每年的国内生产总值都按得增长率6.1%增长,那么2021年的国内生产总值为( )
A.105.13万亿元 B.111.54万亿元 C.118.35万亿元 D.116.2万亿元
4.甲、乙两物体分别从相距70m的两处同时相向运动.甲第1分钟走2m,以后每分钟比前一分钟多走1m,乙每分钟走5m,如果甲、乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1m,乙继续每分钟走5m.那么从开始运动( )分钟后第二次相遇.
A.5 B.7 C.15 D.18
5.某银行设立了教育助学低息贷款,其中规定一年期以上贷款月均等额还本付息(利息按月以复利计算).如果小新同学贷款10000元,一年还清,假设月利率为0.25%,那么小新同学每月应还的钱约为( )(1.002512≈1.03)
A.833 B.858 C.883 D.902
6.我国古代数学名著《算法统宗》中说:九百九十六斤棉,赠分八子做盘缠;次第每人多十七,要将第八数来言;务要分明依次第,孝和休惹外人传,说的是,有斤棉花全部赠送给个子女做旅费,从第个孩子开始,以后每人依次多斤,直到第个孩子为止.在这个问题中,第个孩子分到的棉花为( )
A.斤 B.斤 C.斤 D.斤
7.我国工农业总产值从年到年的年间翻了两番,设平均每年的增长率为,则有( )
A. B.
C. D.
8.调查表明,酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过如果某人喝了少量酒后,血液中酒精含量将迅速上升到,在停止喝酒后,血液中酒精含量就以每小时的速度减小,问他至少要经过几小时才可以加强机动车(精确到小时)( )
A.1小时 B.2小时 C.4小时 D.6小时
B级 综合应用
9.某林厂现在的森林木材存量是1 800万 m3,木材以每年25%的增长率生长,而每年要砍伐固定的木材量为x万 m3,为达到经两次砍伐后木材存量增加50%的目标,则x的值是( )
A.40 B.45
C.50 D.55
10.有一套丛书共6册,计划2018年出版第一册,每两年出版一册,那么出版齐这套丛书的年份是( )
A.2022 B.2024
C.2026 D.2028
二、填空题
11.在数列{an}中,若a4=1,a12=5,且任意连续三项的和都是15,则a2018=______.
12.今年元旦,市民小王向朋友小李借款100万元用于购房,双方约定年利率为,按复利计算(即本年利息计入次年本金生息),借款分三次等额归还,从明年的元旦开始,连续三年都是在元旦还款,则每次的还款额是__________元.(四舍五入,精确到整数)
13.已知衡量病毒传播能力的最重要指标叫做传播指数.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是确诊病例增长率×系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确诊病例的平均增长率为40%,两例连续病例的间隔时间的平均数5天,根据以上计算,若甲得这种传染病,则4轮传播后由甲引起的得病的总人数约为__________.
14.党的十九大明确把精准脱贫作为决胜全面建设小康社会必须打好的三个攻坚战之一,作出了新的部署.某地区现有万农村贫困人口,如果计划在未来年内完成脱贫任务,并且后一年的脱贫任务是前一年的一半,为了按时完成脱贫攻坚任务,那么第一年需要完成的脱贫任务是______万人.
C级 拓展探究
三、解答题
15.某公司自2020年起,每年投入的设备升级资金为500万元,预计自2020年起(2020年为第1年),因为设备升级,第n年可新增的盈利(单位:万元),求:
(1)第几年起,当年新增盈利超过当年设备升级资金;
(2)第几年起,累计新增盈利总额超过累计设备升级资金总额.
16.已知数列中,,数列的前n项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)求证:.
参考答案
1.D
【分析】
根据单利计算公式直接计算第5年的本利和.
【详解】
因为是按照单利计算,所以第5年的利息是,
第五年末的本利和是.
故选:D
2.D
【分析】
利用每年后的价值成等比数列,可求得结果.
【详解】
依题意可知第一年后的价值为 ,第二年后的价值为,
依此类推可知每年后的价值成等比数列,其首项,公比为,
所以年后这批设备的价值为.
故选:D。
【点睛】
本题考查了数列的简单应用,考查了等比数列的通项公式,属于基础题.
3.A
【分析】
根据2020年初国内生产总值为99.0865万亿,然后计算99.0865(1+6.1%),可得结果.
【详解】
由题可知:2020年初国内生产总值为99.0865万亿
则2021年的国内生产总值为99.0865(1+6.1%)=105.13万亿元
故选:A
【点睛】
本题考查等比数列在实际应用中的应用,理清思路,审清题意,属基础题.
4.C
【分析】
设n分钟后第2次相遇,使用等差数列的前项和公式,列出式子2n++5n=3×70,简单计算,可得结果.
【详解】
设n分钟后第2次相遇,
依题意:2n++5n=3×70,
整理得n2+13n-6×70=0,
解得n=15,n=-28(舍去).
故第2次相遇是在开始运动后15min.
故选:C
【点睛】
本题考查等差数列的前项和公式的应用,重在审清题意,属基础题.
5.B
【分析】
先计算本息和,然后假设每月应还钱数,根据等比数列求和公式,列出式子,最后简单计算,可得结果.
【详解】
贷款10000元两年到期时本金与利息之和为:
10000×(1+0. 25%)12=10000×1.002512(元).
设每月还x元,
则x+1.0025x+…+1.002512x=
即≈10300
所以x≈858(元),即每月应还858元.
故选:B
【点睛】
本题考查等比数列在实际中的应用,审清题意,细心计算,属基础题.
6.C
【分析】
设第一个孩子分配到斤棉花,利用等差数列前项和公式得:,解方程从而得到.
【详解】
解:设第一个孩子分配到斤棉花,
则由题意得:,
解得=65,
故选:C.
【点睛】
本题考查等差数列首项的求法,是基础题,解题时要认真审题,注意等差数列的公式的合理运用.
7.D
【分析】
设的总产值为,我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的倍,然后根据平均增长率的定义列等式即可.
【详解】
本题为增长率模型函数,为指数函数形式.
设年总产值为,由于我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的,则.
故选D.
【点睛】
本题考查平均增长律的定义,根据题意列式是解本题的关键,考查分析问题和解决问题的能力,属于基础题.
8.C
【分析】
设n个小时后才可以驾车,由题意得方程,解得即可.
【详解】
设n个小时后才可以驾车,根据题意可知,每小时酒精下降的量成等比数列,公比为进而可得方程得,即,所以至少要经过4小时后才可以驾驶机动车.
故选C.
【点睛】
本题主要考查了等比数列的性质及实际应用,考查了学生运用所学知识解决实际问题的能力,属于基础题.
9.C
【分析】
分成两次来计算,首先计算第一年砍伐和增长后得到的,然后再算第二年砍伐和增长后得到的,结合木材增加列方程,可求得的值.
【详解】
经过一次刊发后,木材存量为,经过两次砍伐后,木材存量为.由题意有,解得,故选.
【点睛】
本小题主要考查增长和减少同时进行的实际问题,由于题目砍伐的次数只有两次,所以只需要计算两次,按的增长要求列出方程,可求得的值.属于中档题.
10.D
【分析】
由2018年出版第一册,每两年出版一册,可得出版齐这套丛书共需10年,从而可得结果.
【详解】
因为2018年出版第一册,每两年出版一册,
所以2020年出版第二册;
2022年出版第三册;
2024年出版第四册;
2026年出版第五册;
2028年出版第六册;
即出版齐这套丛书的年份是2028年,故选D.
【点睛】
本题主要考查阅读能力以及数列的实际应用,属于简单题.
11.9
【解析】
分析:将an+an+1+an+2=15中n换为n+1,可得数列{an}是周期为3的数列.求出a2,a1,即可得到a2018
详解:由题意可得an+an+1+an+2=15,将n换为an+1+an+2+an+3=15,可得an+3=an,可得数列{an是周期为3的数列.故,由an+an+1+an+2=15,n取1可得,故,故答案为9.
点睛:本题考查了数列的周期性、递推关系,考查了推理能力与计算能力,属于中档题.
12.
【分析】
先设每次的还款额为元,贷款额为元,根据题中条件,逐年列出欠款,根据题中条件,列出方程求解,即可得出结果.
【详解】
设每次的还款额为元,记贷款额为元,
由题意,第一次还款后欠款额为;
第二次还款后欠款额为,
第三次还款后欠款额为,
因为三次将欠款还完,所以,
整理得,
解得元.
故答案为:.
13.120
【分析】
先求出传播指数RO,再计算出每轮感染的人数,相加即得.
【详解】
由题意知,,
所以得病总人数为:(人).
故答案为:120
【点睛】
本题考查数列的应用,解题关键是理解新概念“传播指数”,可以用数列表示该问题,传播指数就是等比数列的公比,属基础题.
14.16
【分析】
设第三年脱贫人口为x万,则第二年脱贫人口为2x万,第一年脱贫人口为4x万,根据题意列出方程求解x即可得解.
【详解】
设第三年脱贫人口为x万,根据题意,第二年脱贫人口为2x万,第一年脱贫人口为4x万,
三年完成脱贫任务则,解得,
所以第一年脱贫人口应为16万.
故答案为:16
【点睛】
本题考查材料解析,属于基础题.
15.(1)第7年;(2)第12年.
【分析】
(1)分段解不等式,(2)对进行讨论,求的前项和,令,解不等式.
【详解】
(1)当时,,解得,即,不成立,
当时,,即,随着的增大而减小,
当时,不成立,当时,成立,
故第7年起,当年新增盈利超过当年设备升级资金;
(2)当时,累计新增盈利总额
,
可得所求超过5,
当时,,
整理得,由于随着的增大而减小
又当时,,故不成立,
当时,,故成立,
故从第12年起,累计新增盈利总额超过累计设备升级资金总额.
16.(Ⅰ);(Ⅱ)证明见解析.
【分析】
(Ⅰ)根据题意中表达式,令,可求得表达式,两式相减,根据,即可求得数列的通项公式,经检验n=1满足题意,即可得答案;
(Ⅱ)根据(Ⅰ)可得,即可进行证明,经检验n=1满足题意,即可得证.
【详解】
(Ⅰ)由可得,两式相减,
所以,又(满足上式),
所以.
(Ⅱ)由(Ⅰ)可知,
所以,
又满足题意,
所以对于任意,都有.
A级 巩固基础
一、单选题
1.按活期存入银行1000元,年利率是0.52%,那么按照单利,第5年末的本利和是( )
A.1036元 B.1028元 C.1043元 D.1026元
2.一批设备价值万元,由于使用磨损,每年比上一年价值降低,则年后这批设备的价值为( )
A. B. C. D.
3.2019年我国国内生产总值增长率为6.1%,达到了990865亿元,实现了新的跨越,2020年我们将全面建成小康社会,实现第一个一百年的奋斗目标.如果从2020年初开始,以后每年的国内生产总值都按得增长率6.1%增长,那么2021年的国内生产总值为( )
A.105.13万亿元 B.111.54万亿元 C.118.35万亿元 D.116.2万亿元
4.甲、乙两物体分别从相距70m的两处同时相向运动.甲第1分钟走2m,以后每分钟比前一分钟多走1m,乙每分钟走5m,如果甲、乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1m,乙继续每分钟走5m.那么从开始运动( )分钟后第二次相遇.
A.5 B.7 C.15 D.18
5.某银行设立了教育助学低息贷款,其中规定一年期以上贷款月均等额还本付息(利息按月以复利计算).如果小新同学贷款10000元,一年还清,假设月利率为0.25%,那么小新同学每月应还的钱约为( )(1.002512≈1.03)
A.833 B.858 C.883 D.902
6.我国古代数学名著《算法统宗》中说:九百九十六斤棉,赠分八子做盘缠;次第每人多十七,要将第八数来言;务要分明依次第,孝和休惹外人传,说的是,有斤棉花全部赠送给个子女做旅费,从第个孩子开始,以后每人依次多斤,直到第个孩子为止.在这个问题中,第个孩子分到的棉花为( )
A.斤 B.斤 C.斤 D.斤
7.我国工农业总产值从年到年的年间翻了两番,设平均每年的增长率为,则有( )
A. B.
C. D.
8.调查表明,酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过如果某人喝了少量酒后,血液中酒精含量将迅速上升到,在停止喝酒后,血液中酒精含量就以每小时的速度减小,问他至少要经过几小时才可以加强机动车(精确到小时)( )
A.1小时 B.2小时 C.4小时 D.6小时
B级 综合应用
9.某林厂现在的森林木材存量是1 800万 m3,木材以每年25%的增长率生长,而每年要砍伐固定的木材量为x万 m3,为达到经两次砍伐后木材存量增加50%的目标,则x的值是( )
A.40 B.45
C.50 D.55
10.有一套丛书共6册,计划2018年出版第一册,每两年出版一册,那么出版齐这套丛书的年份是( )
A.2022 B.2024
C.2026 D.2028
二、填空题
11.在数列{an}中,若a4=1,a12=5,且任意连续三项的和都是15,则a2018=______.
12.今年元旦,市民小王向朋友小李借款100万元用于购房,双方约定年利率为,按复利计算(即本年利息计入次年本金生息),借款分三次等额归还,从明年的元旦开始,连续三年都是在元旦还款,则每次的还款额是__________元.(四舍五入,精确到整数)
13.已知衡量病毒传播能力的最重要指标叫做传播指数.它指的是,在自然情况下(没有外力介入,同时所有人都没有免疫力),一个感染到某种传染病的人,会把疾病传染给多少人的平均数.它的简单计算公式是确诊病例增长率×系列间隔,其中系列间隔是指在一个传播链中,两例连续病例的间隔时间(单位:天).根据统计,确诊病例的平均增长率为40%,两例连续病例的间隔时间的平均数5天,根据以上计算,若甲得这种传染病,则4轮传播后由甲引起的得病的总人数约为__________.
14.党的十九大明确把精准脱贫作为决胜全面建设小康社会必须打好的三个攻坚战之一,作出了新的部署.某地区现有万农村贫困人口,如果计划在未来年内完成脱贫任务,并且后一年的脱贫任务是前一年的一半,为了按时完成脱贫攻坚任务,那么第一年需要完成的脱贫任务是______万人.
C级 拓展探究
三、解答题
15.某公司自2020年起,每年投入的设备升级资金为500万元,预计自2020年起(2020年为第1年),因为设备升级,第n年可新增的盈利(单位:万元),求:
(1)第几年起,当年新增盈利超过当年设备升级资金;
(2)第几年起,累计新增盈利总额超过累计设备升级资金总额.
16.已知数列中,,数列的前n项和为,且.
(Ⅰ)求数列的通项公式;
(Ⅱ)求证:.
参考答案
1.D
【分析】
根据单利计算公式直接计算第5年的本利和.
【详解】
因为是按照单利计算,所以第5年的利息是,
第五年末的本利和是.
故选:D
2.D
【分析】
利用每年后的价值成等比数列,可求得结果.
【详解】
依题意可知第一年后的价值为 ,第二年后的价值为,
依此类推可知每年后的价值成等比数列,其首项,公比为,
所以年后这批设备的价值为.
故选:D。
【点睛】
本题考查了数列的简单应用,考查了等比数列的通项公式,属于基础题.
3.A
【分析】
根据2020年初国内生产总值为99.0865万亿,然后计算99.0865(1+6.1%),可得结果.
【详解】
由题可知:2020年初国内生产总值为99.0865万亿
则2021年的国内生产总值为99.0865(1+6.1%)=105.13万亿元
故选:A
【点睛】
本题考查等比数列在实际应用中的应用,理清思路,审清题意,属基础题.
4.C
【分析】
设n分钟后第2次相遇,使用等差数列的前项和公式,列出式子2n++5n=3×70,简单计算,可得结果.
【详解】
设n分钟后第2次相遇,
依题意:2n++5n=3×70,
整理得n2+13n-6×70=0,
解得n=15,n=-28(舍去).
故第2次相遇是在开始运动后15min.
故选:C
【点睛】
本题考查等差数列的前项和公式的应用,重在审清题意,属基础题.
5.B
【分析】
先计算本息和,然后假设每月应还钱数,根据等比数列求和公式,列出式子,最后简单计算,可得结果.
【详解】
贷款10000元两年到期时本金与利息之和为:
10000×(1+0. 25%)12=10000×1.002512(元).
设每月还x元,
则x+1.0025x+…+1.002512x=
即≈10300
所以x≈858(元),即每月应还858元.
故选:B
【点睛】
本题考查等比数列在实际中的应用,审清题意,细心计算,属基础题.
6.C
【分析】
设第一个孩子分配到斤棉花,利用等差数列前项和公式得:,解方程从而得到.
【详解】
解:设第一个孩子分配到斤棉花,
则由题意得:,
解得=65,
故选:C.
【点睛】
本题考查等差数列首项的求法,是基础题,解题时要认真审题,注意等差数列的公式的合理运用.
7.D
【分析】
设的总产值为,我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的倍,然后根据平均增长率的定义列等式即可.
【详解】
本题为增长率模型函数,为指数函数形式.
设年总产值为,由于我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的,则.
故选D.
【点睛】
本题考查平均增长律的定义,根据题意列式是解本题的关键,考查分析问题和解决问题的能力,属于基础题.
8.C
【分析】
设n个小时后才可以驾车,由题意得方程,解得即可.
【详解】
设n个小时后才可以驾车,根据题意可知,每小时酒精下降的量成等比数列,公比为进而可得方程得,即,所以至少要经过4小时后才可以驾驶机动车.
故选C.
【点睛】
本题主要考查了等比数列的性质及实际应用,考查了学生运用所学知识解决实际问题的能力,属于基础题.
9.C
【分析】
分成两次来计算,首先计算第一年砍伐和增长后得到的,然后再算第二年砍伐和增长后得到的,结合木材增加列方程,可求得的值.
【详解】
经过一次刊发后,木材存量为,经过两次砍伐后,木材存量为.由题意有,解得,故选.
【点睛】
本小题主要考查增长和减少同时进行的实际问题,由于题目砍伐的次数只有两次,所以只需要计算两次,按的增长要求列出方程,可求得的值.属于中档题.
10.D
【分析】
由2018年出版第一册,每两年出版一册,可得出版齐这套丛书共需10年,从而可得结果.
【详解】
因为2018年出版第一册,每两年出版一册,
所以2020年出版第二册;
2022年出版第三册;
2024年出版第四册;
2026年出版第五册;
2028年出版第六册;
即出版齐这套丛书的年份是2028年,故选D.
【点睛】
本题主要考查阅读能力以及数列的实际应用,属于简单题.
11.9
【解析】
分析:将an+an+1+an+2=15中n换为n+1,可得数列{an}是周期为3的数列.求出a2,a1,即可得到a2018
详解:由题意可得an+an+1+an+2=15,将n换为an+1+an+2+an+3=15,可得an+3=an,可得数列{an是周期为3的数列.故,由an+an+1+an+2=15,n取1可得,故,故答案为9.
点睛:本题考查了数列的周期性、递推关系,考查了推理能力与计算能力,属于中档题.
12.
【分析】
先设每次的还款额为元,贷款额为元,根据题中条件,逐年列出欠款,根据题中条件,列出方程求解,即可得出结果.
【详解】
设每次的还款额为元,记贷款额为元,
由题意,第一次还款后欠款额为;
第二次还款后欠款额为,
第三次还款后欠款额为,
因为三次将欠款还完,所以,
整理得,
解得元.
故答案为:.
13.120
【分析】
先求出传播指数RO,再计算出每轮感染的人数,相加即得.
【详解】
由题意知,,
所以得病总人数为:(人).
故答案为:120
【点睛】
本题考查数列的应用,解题关键是理解新概念“传播指数”,可以用数列表示该问题,传播指数就是等比数列的公比,属基础题.
14.16
【分析】
设第三年脱贫人口为x万,则第二年脱贫人口为2x万,第一年脱贫人口为4x万,根据题意列出方程求解x即可得解.
【详解】
设第三年脱贫人口为x万,根据题意,第二年脱贫人口为2x万,第一年脱贫人口为4x万,
三年完成脱贫任务则,解得,
所以第一年脱贫人口应为16万.
故答案为:16
【点睛】
本题考查材料解析,属于基础题.
15.(1)第7年;(2)第12年.
【分析】
(1)分段解不等式,(2)对进行讨论,求的前项和,令,解不等式.
【详解】
(1)当时,,解得,即,不成立,
当时,,即,随着的增大而减小,
当时,不成立,当时,成立,
故第7年起,当年新增盈利超过当年设备升级资金;
(2)当时,累计新增盈利总额
,
可得所求超过5,
当时,,
整理得,由于随着的增大而减小
又当时,,故不成立,
当时,,故成立,
故从第12年起,累计新增盈利总额超过累计设备升级资金总额.
16.(Ⅰ);(Ⅱ)证明见解析.
【分析】
(Ⅰ)根据题意中表达式,令,可求得表达式,两式相减,根据,即可求得数列的通项公式,经检验n=1满足题意,即可得答案;
(Ⅱ)根据(Ⅰ)可得,即可进行证明,经检验n=1满足题意,即可得证.
【详解】
(Ⅰ)由可得,两式相减,
所以,又(满足上式),
所以.
(Ⅱ)由(Ⅰ)可知,
所以,
又满足题意,
所以对于任意,都有.
