第一章 抛体运动 单元提高卷 Word版含解析
文档属性
| 名称 | 第一章 抛体运动 单元提高卷 Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 548.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-08 09:53:01 | ||
图片预览



文档简介
第一章
1.(多选)一艘船过河时,船头始终与船实际运动的方向垂直,水速恒为v1,船相对于水的速度大小恒为v2,船过河的时间为t,则( )
A.v1有可能等于v2
B.船的实际速度大小为
C.船头方向与河岸上游的夹角θ大小满足cos θ=
D.河宽为t
【答案】CD
【解析】由于船相对于水的速度始终与船实际运动的方向垂直,即船相对于水的速度始终与船实际速度v垂直,由几何关系可知,v1大于v2,A错误;船的实际速度大小为,B错误;cos θ=,C正确;河宽为v2tsin θ=t,D正确.
2.人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度v0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度是( )
A.v0sin θ B.
C.v0cos θ D.
【答案】D
【解析】由运动的合成与分解可知,物体A参与这样的两个分运动,一个是沿着与它相连接的绳子方向的运动,另一个是垂直于绳子斜向上的运动.而物体A实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A的合运动.它们之间的关系如图所示.由三角函数知识,可得vA=,所以D正确.
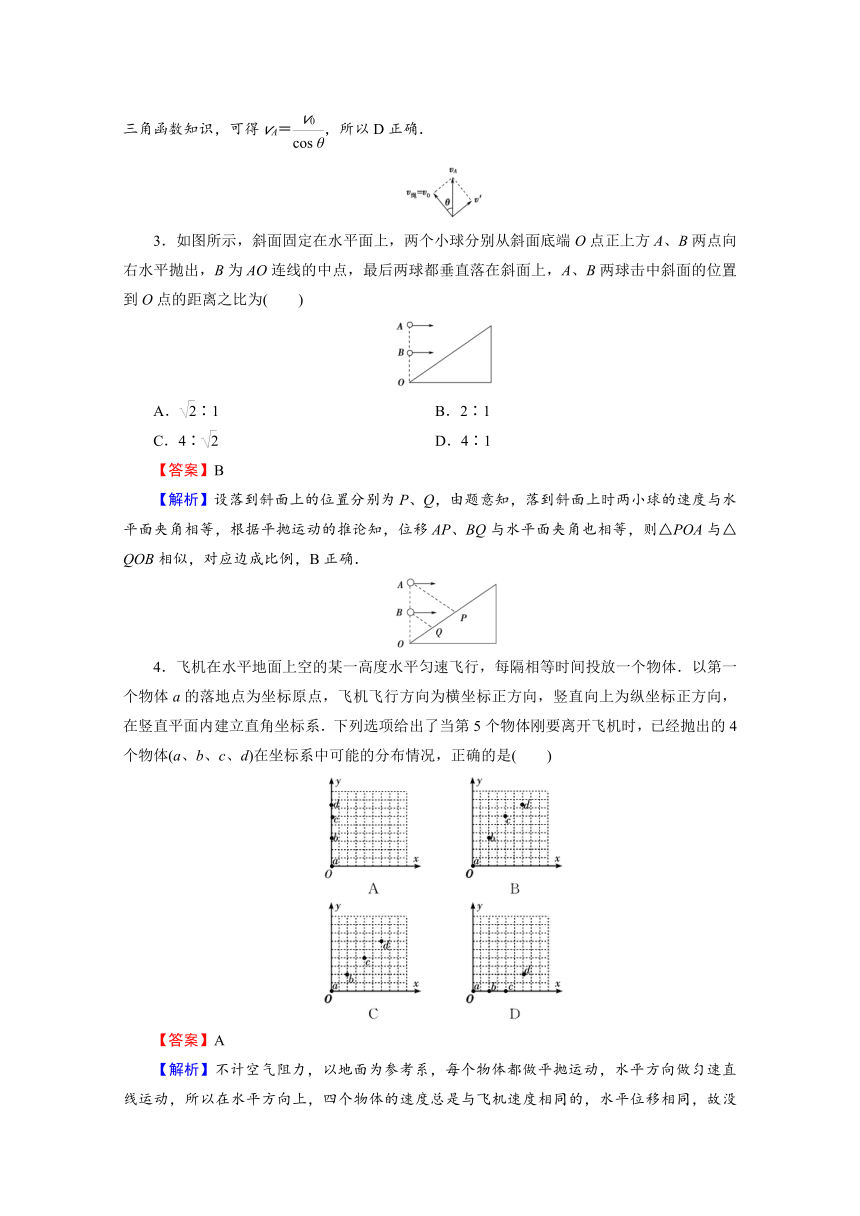
3.如图所示,斜面固定在水平面上,两个小球分别从斜面底端O点正上方A、B两点向右水平抛出,B为AO连线的中点,最后两球都垂直落在斜面上,A、B两球击中斜面的位置到O点的距离之比为( )
A.∶1 B.2∶1
C.4∶ D.4∶1
【答案】B
【解析】设落到斜面上的位置分别为P、Q,由题意知,落到斜面上时两小球的速度与水平面夹角相等,根据平抛运动的推论知,位移AP、BQ与水平面夹角也相等,则△POA与△QOB相似,对应边成比例,B正确.
4.飞机在水平地面上空的某一高度水平匀速飞行,每隔相等时间投放一个物体.以第一个物体a的落地点为坐标原点,飞机飞行方向为横坐标正方向,竖直向上为纵坐标正方向,在竖直平面内建立直角坐标系.下列选项给出了当第5个物体刚要离开飞机时,已经抛出的4个物体(a、b、c、d)在坐标系中可能的分布情况,正确的是( )
【答案】A
【解析】不计空气阻力,以地面为参考系,每个物体都做平抛运动,水平方向做匀速直线运动,所以在水平方向上,四个物体的速度总是与飞机速度相同的,水平位移相同,故没有位移差,看起来在一条竖直线上;竖直方向做自由落体运动,最先释放的物体间的距离大些,相当于同一个物体做自由落体运动在不同时刻的位置,故A正确,B、C错误;D中a、b、c三个物体落到地面,水平方向间隔2个格,c和d在水平方向也间隔2个格,那么d也一定落到地面,从图像可得d并未落到地面,所以D错误.
5.如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端c处.在c点正上方且与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的三等分点d处.若不计空气阻力,下列关系式正确的是( )
A.ta=tb B.ta=3tb
C.va=vb D.va=vb
【答案】C
【解析】由于a、b两球下降的高度之比为3∶1,根据h=gt2可知下落时间t=,则两小球运动的时间关系是ta=tb,故A、B错误;因为两球水平位移之比为3∶2,由v0=,得va=vb,故C正确,D错误.
6.如图所示,将一小球从斜面上方的P点沿不同的方向以相同的速率抛出,不计空气阻力.要使得小球从抛出到落到斜面的时间最短,小球抛出的方向是( )
A.水平向左 B.竖直向下
C.垂直斜面向下 D.平行于斜面向下
【答案】C
【解析】小球抛出后加速度都为g,方向竖直向下,各个小球垂直于斜面方向的分加速度相等.由x=v0t+at2,x、a相等,垂直斜面向下抛出时垂直斜面向下方向的分初速度最大,所用时间最短,故C正确,B、C、D错误.
7.质量m=2 kg的物体(可视为质点)静止在光滑水平面上的直角坐标系的原点处,先用沿x轴正方向的力F1=8 N作用2 s,然后撤去F1;再用沿y轴正方向的力F2=10 N作用2 s.则物体在这4 s内的轨迹为( )
A B
C D
【答案】D
【解析】物体在F1的作用下由静止开始从坐标系原点沿x轴正方向做匀加速直线运动,加速度a1==4 m/s2,末速度v1=a1t1=8 m/s,对应位移x1=a1t=8 m;到2 s末撤去F1再受到沿y轴正方向的力F2的作用,物体在x轴正方向做匀速运动,x2=v1t2=16 m,在y轴正方向做匀加速运动,y轴正方向的加速度a2==5 m/s2,对应的位移y=a2t=10 m,物体做曲线运动.再根据曲线运动的加速度方向大致指向轨迹的凹侧,可知A、B、C均错误,D正确.
8.光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角(如图所示),与此同时对质点施加沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
A.因为有Fx,质点一定做曲线运动
B.如果Fy>Fx,质点向y轴一侧做曲线运动
C.质点不可能做直线运动
D.如果Fx>Fycot α,质点向x轴一侧做曲线运动
【答案】D
【解析】若Fx=Fycot α,则合力方向与速度方向在同一条直线上,物体做直线运动,A、C错误;因为不确定cot α的大小,所以无法通过比较Fy与Fx的大小来确定质点向哪一侧做曲线运动,B错误;若Fx>Fycot α,则合力方向与速度方向不在同一条直线上,合力偏向于速度方向下侧,质点向x轴一侧做曲线运动,故D正确.
9.(多选)如图所示,长为l的轻杆,一端固定一个质量为m的小球,另一端有固定转动轴O,杆可在竖直面内绕转动轴O无摩擦转动.质量为m的物块放置在光滑水平面上.开始时,使小球靠在物块的光滑侧面上,轻杆与水平面夹角为45°,用手控制物块静止.然后释放物块,此后球与物块运动的过程中,下列说法正确的是( )
A.球与物块分离前,球与物块速度相等
B.球与物块分离前,物块速度逐渐增大
C.球与物块分离前,杆上弹力逐渐增大
D.球与物块分离时,球加速度等于重力加速度g
【答案】BD
【解析】设球的速度为v,根据题意得物块与球的水平速度相等,设杆与地面夹角为θ,由运动的分解有vx=vsin θ,所以分离前,球与物块速度不相等,A错误;由于地面光滑,球水平方向只受到杆对球的弹力,所以分离前,物块受力即加速度始终向左,一直加速,B正确;对小球和物块整体受力分析,受重力、杆的弹力F、地面的支持力FN,在水平方向运用牛顿第二定律得Fcos θ=(M+m)ax.根据题意知,水平方向加速度逐渐变小,所以弹力变小,当恰好分离时,水平加速度为零,弹力为零,球只受重力,加速度为g,C错误,D正确.
10.(多选)“嫦娥四号”探月卫星的成功发射,标志着我国航天技术又迈上了一个新台阶.将来我国宇航员还会乘坐探月卫星登上月球,如图所示是宇航员在月球表面水平抛出小球的闪光照片的一部分.已知照片上小方格代表的实际边长为a,闪光周期为T,据此可知( )
A.月球上的重力加速度为
B.小球平抛的初速度为
C.照片上A点一定是平抛的起始位置
D.小球运动到D点时速度大小为
【答案】BC
【解析】由闪光照片可知,小球竖直方向位移差Δy=2a,由Δy=gT2,可得月球上的重力加速度g=,A错误;由小球在水平方向做匀速直线运动,可得3a=v0T,解得v0=,B正确;小球在平抛出后第一个T时间内竖直方向位移y1=gT2=××T2=a,所以照片上A点一定是平抛的起始位置,C正确;小球运动到D点时竖直速度vy=g·3T=·3T=,水平速度为v0=,小球运动到D点时速度大小v==,D错误.
11.如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球落在圆环时的时间越长
B.即使v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角也相同
C.若v0取值适当,可以使小球垂直撞击半圆环
D.无论v0取何值,小球都不可能垂直撞击半圆环
【答案】D
【解析】小球落在环上的最低点C时时间最长,所以A错误;v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角不相同,B错误;要使小球垂直撞击半圆环.设小球落点与圆心的连线与水平方向夹角为θ,根据平抛运动规律,v0t=R(1+cos θ),Rsin θ=gt2,tan θ=,联立解得cos θ=1,即垂直撞击到B点,这是不可能的,所以D正确,C错误.
12.图甲是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹.
(1)以下是实验过程中的一些做法,其中合理的有________.
a.安装斜槽轨道,使其末端保持水平
b.每次小球释放的初始位置可以任意选择
c.每次小球应从同一高度由静止释放
d.为描出小球的运动轨迹,描绘的点可以用折线连接
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图乙中y-x2图像能说明平抛小球运动轨迹为抛物线的是________.
(3)图丙是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取两点A、B,测得A、B两点纵坐标y1=5.0 cm,y2=45.0 cm,A、B两点水平间距Δx=40.0 cm.则平抛小球的初速度v0=________m/s.
【答案】(1)ac (2)c (3)2.0
【解析】 (1)为了保证小球的初速度水平,安装斜槽轨道时,斜槽末端必须保持水平,故a正确;为了保证小球每次平抛运动的初速度相等,每一次让小球从斜槽的同一位置由静止释放,故b错误,c正确;为描出小球的运动轨迹,描绘的点要用平滑曲线连接,故d错误.
(2)根据平抛运动的规律有x=v0t,y=gt2,得y==kx2,其中k==定值,可知y与x2的图线是过原点的倾斜直线,因此,题图乙中y-x2图像能说明平抛小球运动轨迹为抛物线的是c.
(3)根据y1=gt,得t1=,
根据y2=gt,得t2=,
则小球的初速度v0=.
已知y1=5.0 cm=0.05 m,y2=45.0 cm=0.45 m,Δx=40.0 cm=0.4 m,代入上式解得v0≈2.0 m/s.
13.如图所示,水平屋顶高h0=5 m,围墙高h=3.2 m,围墙到房子的水平距离l=3 m,围墙外空地宽x=10 m.g取10 m/s2.为使小球从屋顶水平飞出落在围墙外的空地上,求:
(1)小球离开屋顶时速度v0的大小范围.
(2)小球落在空地上的最小速度.
【答案】(1)5 m/s≤v0≤13 m/s (2)5 m/s
【解析】(1)设小球恰好落到空地的右侧边缘时的水平初速度为v01,则小球的水平位移为l+x=v01t1.
小球的竖直位移h0=gt,
解以上两式得v01=(l+x)=13 m/s.
设小球恰好越过围墙的边缘时的水平初速度为v02,则此过程中小球的水平位移l=v02t2,
小球的竖直位移h0-h=gt,
解以上两式得v02=l=5 m/s,
小球离开屋顶时的速度大小为5 m/s≤v0≤13 m/s.
(2)小球落在空地上,下落高度一定,落地时的竖直分速度一定,当小球恰好越过围墙的边缘落在空地上时,落地速度最小.
竖直方向有v=2gh0,又有vmin=,
解得vmin=5 m/s.
1.(多选)一艘船过河时,船头始终与船实际运动的方向垂直,水速恒为v1,船相对于水的速度大小恒为v2,船过河的时间为t,则( )
A.v1有可能等于v2
B.船的实际速度大小为
C.船头方向与河岸上游的夹角θ大小满足cos θ=
D.河宽为t
【答案】CD
【解析】由于船相对于水的速度始终与船实际运动的方向垂直,即船相对于水的速度始终与船实际速度v垂直,由几何关系可知,v1大于v2,A错误;船的实际速度大小为,B错误;cos θ=,C正确;河宽为v2tsin θ=t,D正确.
2.人用绳子通过定滑轮拉物体A,A穿在光滑的竖直杆上,当以速度v0匀速地拉绳使物体A到达如图所示位置时,绳与竖直杆的夹角为θ,则物体A实际运动的速度是( )
A.v0sin θ B.
C.v0cos θ D.
【答案】D
【解析】由运动的合成与分解可知,物体A参与这样的两个分运动,一个是沿着与它相连接的绳子方向的运动,另一个是垂直于绳子斜向上的运动.而物体A实际运动轨迹是沿着竖直杆向上的,这一轨迹所对应的运动就是物体A的合运动.它们之间的关系如图所示.由三角函数知识,可得vA=,所以D正确.
3.如图所示,斜面固定在水平面上,两个小球分别从斜面底端O点正上方A、B两点向右水平抛出,B为AO连线的中点,最后两球都垂直落在斜面上,A、B两球击中斜面的位置到O点的距离之比为( )
A.∶1 B.2∶1
C.4∶ D.4∶1
【答案】B
【解析】设落到斜面上的位置分别为P、Q,由题意知,落到斜面上时两小球的速度与水平面夹角相等,根据平抛运动的推论知,位移AP、BQ与水平面夹角也相等,则△POA与△QOB相似,对应边成比例,B正确.
4.飞机在水平地面上空的某一高度水平匀速飞行,每隔相等时间投放一个物体.以第一个物体a的落地点为坐标原点,飞机飞行方向为横坐标正方向,竖直向上为纵坐标正方向,在竖直平面内建立直角坐标系.下列选项给出了当第5个物体刚要离开飞机时,已经抛出的4个物体(a、b、c、d)在坐标系中可能的分布情况,正确的是( )
【答案】A
【解析】不计空气阻力,以地面为参考系,每个物体都做平抛运动,水平方向做匀速直线运动,所以在水平方向上,四个物体的速度总是与飞机速度相同的,水平位移相同,故没有位移差,看起来在一条竖直线上;竖直方向做自由落体运动,最先释放的物体间的距离大些,相当于同一个物体做自由落体运动在不同时刻的位置,故A正确,B、C错误;D中a、b、c三个物体落到地面,水平方向间隔2个格,c和d在水平方向也间隔2个格,那么d也一定落到地面,从图像可得d并未落到地面,所以D错误.
5.如图所示,在斜面顶端a处以速度va水平抛出一小球,经过时间ta恰好落在斜面底端c处.在c点正上方且与a等高的b处以速度vb水平抛出另一小球,经过时间tb恰好落在斜面的三等分点d处.若不计空气阻力,下列关系式正确的是( )
A.ta=tb B.ta=3tb
C.va=vb D.va=vb
【答案】C
【解析】由于a、b两球下降的高度之比为3∶1,根据h=gt2可知下落时间t=,则两小球运动的时间关系是ta=tb,故A、B错误;因为两球水平位移之比为3∶2,由v0=,得va=vb,故C正确,D错误.
6.如图所示,将一小球从斜面上方的P点沿不同的方向以相同的速率抛出,不计空气阻力.要使得小球从抛出到落到斜面的时间最短,小球抛出的方向是( )
A.水平向左 B.竖直向下
C.垂直斜面向下 D.平行于斜面向下
【答案】C
【解析】小球抛出后加速度都为g,方向竖直向下,各个小球垂直于斜面方向的分加速度相等.由x=v0t+at2,x、a相等,垂直斜面向下抛出时垂直斜面向下方向的分初速度最大,所用时间最短,故C正确,B、C、D错误.
7.质量m=2 kg的物体(可视为质点)静止在光滑水平面上的直角坐标系的原点处,先用沿x轴正方向的力F1=8 N作用2 s,然后撤去F1;再用沿y轴正方向的力F2=10 N作用2 s.则物体在这4 s内的轨迹为( )
A B
C D
【答案】D
【解析】物体在F1的作用下由静止开始从坐标系原点沿x轴正方向做匀加速直线运动,加速度a1==4 m/s2,末速度v1=a1t1=8 m/s,对应位移x1=a1t=8 m;到2 s末撤去F1再受到沿y轴正方向的力F2的作用,物体在x轴正方向做匀速运动,x2=v1t2=16 m,在y轴正方向做匀加速运动,y轴正方向的加速度a2==5 m/s2,对应的位移y=a2t=10 m,物体做曲线运动.再根据曲线运动的加速度方向大致指向轨迹的凹侧,可知A、B、C均错误,D正确.
8.光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角(如图所示),与此同时对质点施加沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
A.因为有Fx,质点一定做曲线运动
B.如果Fy>Fx,质点向y轴一侧做曲线运动
C.质点不可能做直线运动
D.如果Fx>Fycot α,质点向x轴一侧做曲线运动
【答案】D
【解析】若Fx=Fycot α,则合力方向与速度方向在同一条直线上,物体做直线运动,A、C错误;因为不确定cot α的大小,所以无法通过比较Fy与Fx的大小来确定质点向哪一侧做曲线运动,B错误;若Fx>Fycot α,则合力方向与速度方向不在同一条直线上,合力偏向于速度方向下侧,质点向x轴一侧做曲线运动,故D正确.
9.(多选)如图所示,长为l的轻杆,一端固定一个质量为m的小球,另一端有固定转动轴O,杆可在竖直面内绕转动轴O无摩擦转动.质量为m的物块放置在光滑水平面上.开始时,使小球靠在物块的光滑侧面上,轻杆与水平面夹角为45°,用手控制物块静止.然后释放物块,此后球与物块运动的过程中,下列说法正确的是( )
A.球与物块分离前,球与物块速度相等
B.球与物块分离前,物块速度逐渐增大
C.球与物块分离前,杆上弹力逐渐增大
D.球与物块分离时,球加速度等于重力加速度g
【答案】BD
【解析】设球的速度为v,根据题意得物块与球的水平速度相等,设杆与地面夹角为θ,由运动的分解有vx=vsin θ,所以分离前,球与物块速度不相等,A错误;由于地面光滑,球水平方向只受到杆对球的弹力,所以分离前,物块受力即加速度始终向左,一直加速,B正确;对小球和物块整体受力分析,受重力、杆的弹力F、地面的支持力FN,在水平方向运用牛顿第二定律得Fcos θ=(M+m)ax.根据题意知,水平方向加速度逐渐变小,所以弹力变小,当恰好分离时,水平加速度为零,弹力为零,球只受重力,加速度为g,C错误,D正确.
10.(多选)“嫦娥四号”探月卫星的成功发射,标志着我国航天技术又迈上了一个新台阶.将来我国宇航员还会乘坐探月卫星登上月球,如图所示是宇航员在月球表面水平抛出小球的闪光照片的一部分.已知照片上小方格代表的实际边长为a,闪光周期为T,据此可知( )
A.月球上的重力加速度为
B.小球平抛的初速度为
C.照片上A点一定是平抛的起始位置
D.小球运动到D点时速度大小为
【答案】BC
【解析】由闪光照片可知,小球竖直方向位移差Δy=2a,由Δy=gT2,可得月球上的重力加速度g=,A错误;由小球在水平方向做匀速直线运动,可得3a=v0T,解得v0=,B正确;小球在平抛出后第一个T时间内竖直方向位移y1=gT2=××T2=a,所以照片上A点一定是平抛的起始位置,C正确;小球运动到D点时竖直速度vy=g·3T=·3T=,水平速度为v0=,小球运动到D点时速度大小v==,D错误.
11.如图所示,AB为半圆环ACB的水平直径,C为环上的最低点,环半径为R.一个小球从A点以速度v0水平抛出,不计空气阻力,则下列判断正确的是( )
A.v0越大,小球落在圆环时的时间越长
B.即使v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角也相同
C.若v0取值适当,可以使小球垂直撞击半圆环
D.无论v0取何值,小球都不可能垂直撞击半圆环
【答案】D
【解析】小球落在环上的最低点C时时间最长,所以A错误;v0取值不同,小球掉到环上时的速度方向和水平方向之间的夹角不相同,B错误;要使小球垂直撞击半圆环.设小球落点与圆心的连线与水平方向夹角为θ,根据平抛运动规律,v0t=R(1+cos θ),Rsin θ=gt2,tan θ=,联立解得cos θ=1,即垂直撞击到B点,这是不可能的,所以D正确,C错误.
12.图甲是“研究平抛物体运动”的实验装置图,通过描点画出平抛小球的运动轨迹.
(1)以下是实验过程中的一些做法,其中合理的有________.
a.安装斜槽轨道,使其末端保持水平
b.每次小球释放的初始位置可以任意选择
c.每次小球应从同一高度由静止释放
d.为描出小球的运动轨迹,描绘的点可以用折线连接
(2)实验得到平抛小球的运动轨迹,在轨迹上取一些点,以平抛起点O为坐标原点,测量它们的水平坐标x和竖直坐标y,图乙中y-x2图像能说明平抛小球运动轨迹为抛物线的是________.
(3)图丙是某同学根据实验画出的平抛小球的运动轨迹,O为平抛的起点,在轨迹上任取两点A、B,测得A、B两点纵坐标y1=5.0 cm,y2=45.0 cm,A、B两点水平间距Δx=40.0 cm.则平抛小球的初速度v0=________m/s.
【答案】(1)ac (2)c (3)2.0
【解析】 (1)为了保证小球的初速度水平,安装斜槽轨道时,斜槽末端必须保持水平,故a正确;为了保证小球每次平抛运动的初速度相等,每一次让小球从斜槽的同一位置由静止释放,故b错误,c正确;为描出小球的运动轨迹,描绘的点要用平滑曲线连接,故d错误.
(2)根据平抛运动的规律有x=v0t,y=gt2,得y==kx2,其中k==定值,可知y与x2的图线是过原点的倾斜直线,因此,题图乙中y-x2图像能说明平抛小球运动轨迹为抛物线的是c.
(3)根据y1=gt,得t1=,
根据y2=gt,得t2=,
则小球的初速度v0=.
已知y1=5.0 cm=0.05 m,y2=45.0 cm=0.45 m,Δx=40.0 cm=0.4 m,代入上式解得v0≈2.0 m/s.
13.如图所示,水平屋顶高h0=5 m,围墙高h=3.2 m,围墙到房子的水平距离l=3 m,围墙外空地宽x=10 m.g取10 m/s2.为使小球从屋顶水平飞出落在围墙外的空地上,求:
(1)小球离开屋顶时速度v0的大小范围.
(2)小球落在空地上的最小速度.
【答案】(1)5 m/s≤v0≤13 m/s (2)5 m/s
【解析】(1)设小球恰好落到空地的右侧边缘时的水平初速度为v01,则小球的水平位移为l+x=v01t1.
小球的竖直位移h0=gt,
解以上两式得v01=(l+x)=13 m/s.
设小球恰好越过围墙的边缘时的水平初速度为v02,则此过程中小球的水平位移l=v02t2,
小球的竖直位移h0-h=gt,
解以上两式得v02=l=5 m/s,
小球离开屋顶时的速度大小为5 m/s≤v0≤13 m/s.
(2)小球落在空地上,下落高度一定,落地时的竖直分速度一定,当小球恰好越过围墙的边缘落在空地上时,落地速度最小.
竖直方向有v=2gh0,又有vmin=,
解得vmin=5 m/s.
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
