五年级数学下册试题 一课一练《因数与倍数》 苏教版(含答案)
文档属性
| 名称 | 五年级数学下册试题 一课一练《因数与倍数》 苏教版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 38.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 11:43:26 | ||
图片预览

文档简介
《因数与倍数》习题
第一课时
一、填空题。
1.
一个数是3、5、7的倍数,这个数最小是(
)。
2.
是3的倍数的最小三位数是(
)。
3.
一个数是9的倍数,还是72的因数,这个数是(
)。
4.
一个数的最小倍数除以它的最大因数,商是(
)。
5.
一个自然数比20小,它既是2的倍数,又有因数7,这个自然数是(
)。
6.
一个四位数,最高位是3的倍数,百位上是最小的偶数,十位是所有整数共同的因数,个位是奇数,这个数最大是(
)。
二、判断题。
1.
25÷10=2.5,商没有余数,所以25是10的倍数。
(
)
2.
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
(
)
3.
36的全部因数是2、3、4、6、9、12和18,共有7个。
(
)
4.
因为18÷9=2,所以18是倍数,9是因数。
(
)
5.
任何一个自然数最少有两个因数。
(
)
6.
一个数如果是24的倍数,则这个数一定是4和8的倍数。
(
)
7.
因为1.2÷0.6=2,所以1.2是0.6的倍数。
(
)
8.
个位上是3、6、9的数都是3的倍数。
(
)
三、解答题。
1.
王老师拿了32颗糖平均分给一些小朋友,正好分完。小朋友的人数可能是多少?
第二课时
1.
下面的数中,哪些是合数,哪些是质数。
1、13、24、29、41、57、63、79、87
合数有:
质数有:
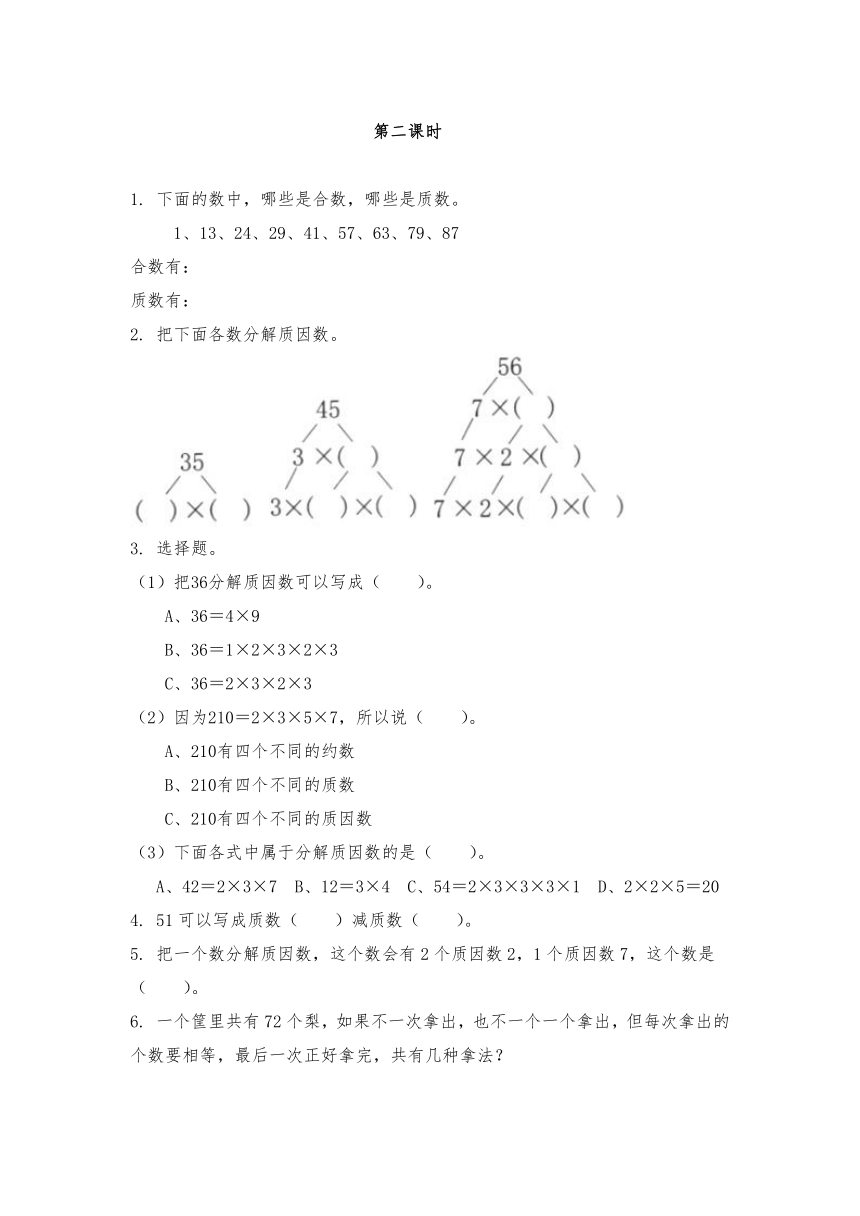
2.
把下面各数分解质因数。
3.
选择题。
(1)把36分解质因数可以写成(
)。
A、36=4×9
B、36=1×2×3×2×3
C、36=2×3×2×3
(2)因为210=2×3×5×7,所以说(
)。
A、210有四个不同的约数
B、210有四个不同的质数
C、210有四个不同的质因数
(3)下面各式中属于分解质因数的是(
)。
A、42=2×3×7
B、12=3×4
C、54=2×3×3×3×1
D、2×2×5=20
4.
51可以写成质数(
)减质数(
)。
5.
把一个数分解质因数,这个数会有2个质因数2,1个质因数7,这个数是(
)。
6.
一个筐里共有72个梨,如果不一次拿出,也不一个一个拿出,但每次拿出的个数要相等,最后一次正好拿完,共有几种拿法?
7.既是质数又是偶数的自然数是(
);既是偶数,又是合数的最小自然数是(
);既是奇数,又是合数的最小自然数是(
);既不是质数,也不是合数的非零自然数是(
)。
8.两个质数的和是18,积是65,这两个质数分别是多少?
9.一个两位质数,交换个位与十位上的数字,所得的两位数仍是质数,这个数是多少?
10.用10以内的质数组成一个三位数,且每个数只能用一次,使它能同时被3、5整除,这个数最小是多少?最大是多少?
11.将下面的8个数分成两组(每组4个数),怎样分才能使两组数的乘积相等?
6、10、14、15、18、21、33、44
12.从小到大写出5个质数,使后面的数都比前面的数大12。
13.把30、33、42、52、65、66、77、78、105九个数分成三组,使每个组的数的乘积相等。
第一课时答案
一、填空题。
1.
105
2.
102
3.
9、18、36或72
4.
1
5.
14
6.
9019
二、判断题。
1.
×
2.
√
3.
×
4.
×
5.
×
6.
√
7.
×
8.
×
三、解答题。
1.
32的因数有:1、2、4、8、16、32。
据题意不可能分给一个小朋友。
答:小朋友的人数可能是2、4、8、16、32人。
第二课时答案
1.
合数有:24,57,63,87
质数有:13,29,41,79
2.
35=5×7
45=3×15=3×3×5
56=7×8=7×2×4=7×2×2×2
3.(1)C
(2)C
(3)A
4.
53
2
5.
28
6.
答:2、3、4、6、8、9、12、18、24、36;所以共有10种拿法。
7.
2,4,9,1
8.
答:这两个质数分别是13和5。
9.
答:13和31;37和73;79和97。(答案不唯一)
10.
答:可以这样想:10以内质数有2、3、5、7;同时能被3、5整除,个位上的数只能是5,这个三位数各数位之和也必须是3的倍数,所以只能用3和7。因此这个数最小是375,最大是735。
11.
把这8个数进行质因数分解,有:
44=11×2×2
33=11×3
21=7×3
18=3×3×2
15=5×3
14=7×2
10=5×2
6=3×2
通过观察可得:(44,21,15,6)和(33,14,10,18)
12.
分别为:5
17
29
41
53。
13.
30=2×3×5
33=3×11
42=2×3×7
52=2×2×13
65=5×13
66=2×3×11
77=7×11
78=2×3×13
105=3×5×7
在这9个数的所有质因数中,一共有6个2,6个3,3个5,3个7,3个11,3个13,所以每组应有2个2,2个3,1个5,1个7,1个11,1个13。
所以这3组分别是(33,52,105)、(77,78,30)、(66,65,42)。
第一课时
一、填空题。
1.
一个数是3、5、7的倍数,这个数最小是(
)。
2.
是3的倍数的最小三位数是(
)。
3.
一个数是9的倍数,还是72的因数,这个数是(
)。
4.
一个数的最小倍数除以它的最大因数,商是(
)。
5.
一个自然数比20小,它既是2的倍数,又有因数7,这个自然数是(
)。
6.
一个四位数,最高位是3的倍数,百位上是最小的偶数,十位是所有整数共同的因数,个位是奇数,这个数最大是(
)。
二、判断题。
1.
25÷10=2.5,商没有余数,所以25是10的倍数。
(
)
2.
一个数的因数的个数是有限的,一个数的倍数的个数是无限的。
(
)
3.
36的全部因数是2、3、4、6、9、12和18,共有7个。
(
)
4.
因为18÷9=2,所以18是倍数,9是因数。
(
)
5.
任何一个自然数最少有两个因数。
(
)
6.
一个数如果是24的倍数,则这个数一定是4和8的倍数。
(
)
7.
因为1.2÷0.6=2,所以1.2是0.6的倍数。
(
)
8.
个位上是3、6、9的数都是3的倍数。
(
)
三、解答题。
1.
王老师拿了32颗糖平均分给一些小朋友,正好分完。小朋友的人数可能是多少?
第二课时
1.
下面的数中,哪些是合数,哪些是质数。
1、13、24、29、41、57、63、79、87
合数有:
质数有:
2.
把下面各数分解质因数。
3.
选择题。
(1)把36分解质因数可以写成(
)。
A、36=4×9
B、36=1×2×3×2×3
C、36=2×3×2×3
(2)因为210=2×3×5×7,所以说(
)。
A、210有四个不同的约数
B、210有四个不同的质数
C、210有四个不同的质因数
(3)下面各式中属于分解质因数的是(
)。
A、42=2×3×7
B、12=3×4
C、54=2×3×3×3×1
D、2×2×5=20
4.
51可以写成质数(
)减质数(
)。
5.
把一个数分解质因数,这个数会有2个质因数2,1个质因数7,这个数是(
)。
6.
一个筐里共有72个梨,如果不一次拿出,也不一个一个拿出,但每次拿出的个数要相等,最后一次正好拿完,共有几种拿法?
7.既是质数又是偶数的自然数是(
);既是偶数,又是合数的最小自然数是(
);既是奇数,又是合数的最小自然数是(
);既不是质数,也不是合数的非零自然数是(
)。
8.两个质数的和是18,积是65,这两个质数分别是多少?
9.一个两位质数,交换个位与十位上的数字,所得的两位数仍是质数,这个数是多少?
10.用10以内的质数组成一个三位数,且每个数只能用一次,使它能同时被3、5整除,这个数最小是多少?最大是多少?
11.将下面的8个数分成两组(每组4个数),怎样分才能使两组数的乘积相等?
6、10、14、15、18、21、33、44
12.从小到大写出5个质数,使后面的数都比前面的数大12。
13.把30、33、42、52、65、66、77、78、105九个数分成三组,使每个组的数的乘积相等。
第一课时答案
一、填空题。
1.
105
2.
102
3.
9、18、36或72
4.
1
5.
14
6.
9019
二、判断题。
1.
×
2.
√
3.
×
4.
×
5.
×
6.
√
7.
×
8.
×
三、解答题。
1.
32的因数有:1、2、4、8、16、32。
据题意不可能分给一个小朋友。
答:小朋友的人数可能是2、4、8、16、32人。
第二课时答案
1.
合数有:24,57,63,87
质数有:13,29,41,79
2.
35=5×7
45=3×15=3×3×5
56=7×8=7×2×4=7×2×2×2
3.(1)C
(2)C
(3)A
4.
53
2
5.
28
6.
答:2、3、4、6、8、9、12、18、24、36;所以共有10种拿法。
7.
2,4,9,1
8.
答:这两个质数分别是13和5。
9.
答:13和31;37和73;79和97。(答案不唯一)
10.
答:可以这样想:10以内质数有2、3、5、7;同时能被3、5整除,个位上的数只能是5,这个三位数各数位之和也必须是3的倍数,所以只能用3和7。因此这个数最小是375,最大是735。
11.
把这8个数进行质因数分解,有:
44=11×2×2
33=11×3
21=7×3
18=3×3×2
15=5×3
14=7×2
10=5×2
6=3×2
通过观察可得:(44,21,15,6)和(33,14,10,18)
12.
分别为:5
17
29
41
53。
13.
30=2×3×5
33=3×11
42=2×3×7
52=2×2×13
65=5×13
66=2×3×11
77=7×11
78=2×3×13
105=3×5×7
在这9个数的所有质因数中,一共有6个2,6个3,3个5,3个7,3个11,3个13,所以每组应有2个2,2个3,1个5,1个7,1个11,1个13。
所以这3组分别是(33,52,105)、(77,78,30)、(66,65,42)。
