2020--2021学年七年级数学 北师大版下册 4.1 认识三角形课件(第1课时 35张)
文档属性
| 名称 | 2020--2021学年七年级数学 北师大版下册 4.1 认识三角形课件(第1课时 35张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 555.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 00:00:00 | ||
图片预览




文档简介
4.1 认识三角形
(第1课时)
北师大版 数学 七年级 下册
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新知
1.认识三角形的概念及基本要素,掌握三角形内角和等于180°.
2. 会把三角形按角分类,熟记直角三角形的性质.
素养目标
3. 会运用三角形内角和定理进行计算.
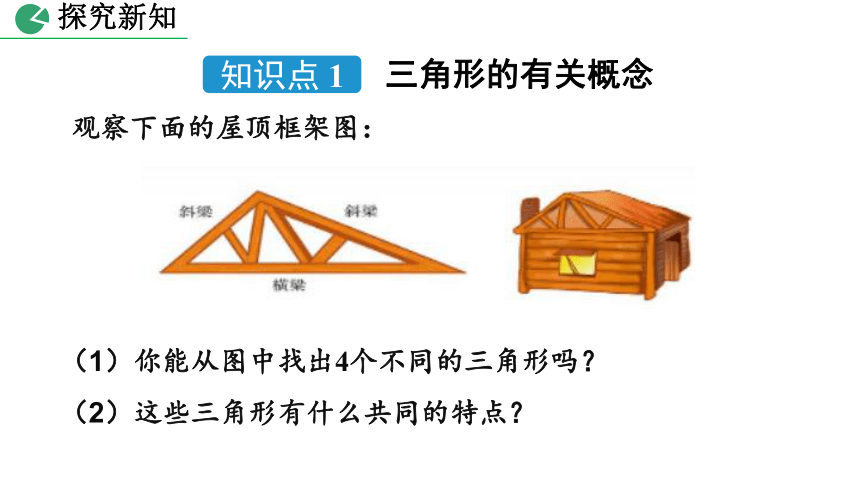
观察下面的屋顶框架图:
(1)你能从图中找出4个不同的三角形吗?
(2)这些三角形有什么共同的特点?
知识点 1
三角形的有关概念
探究新知
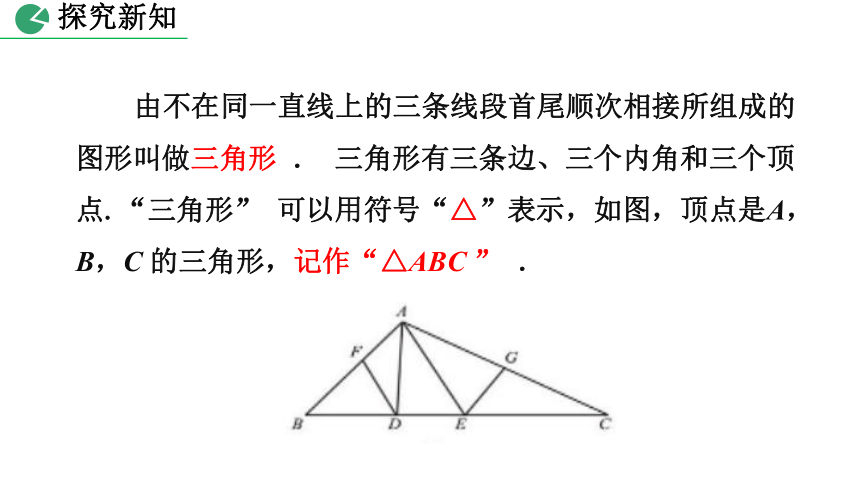
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形 . 三角形有三条边、三个内角和三个顶点.“三角形” 可以用符号“△”表示,如图,顶点是A,B,C 的三角形,记作“△ABC ” .
探究新知
△ABC 的三边,有时也用a,b,c 来表示.如图,顶点A所对的边BC用a表示,边AC,边 AB 分别用b,c来表示.
探究新知
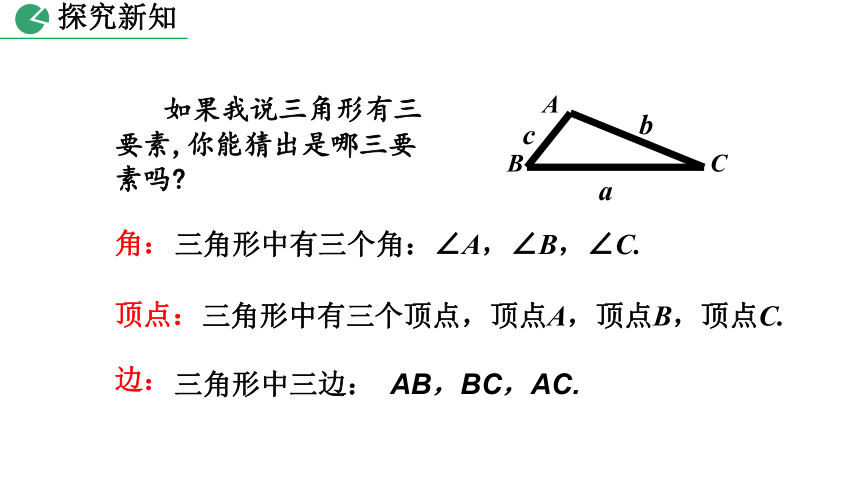
边:
三角形中三边: AB,BC,AC.
如果我说三角形有三要素,你能猜出是哪三要素吗?
A
B
C
b
a
c
角:
三角形中有三个角:∠A,∠B,∠C.
顶点:
三角形中有三个顶点,顶点A,顶点B,顶点C.
探究新知
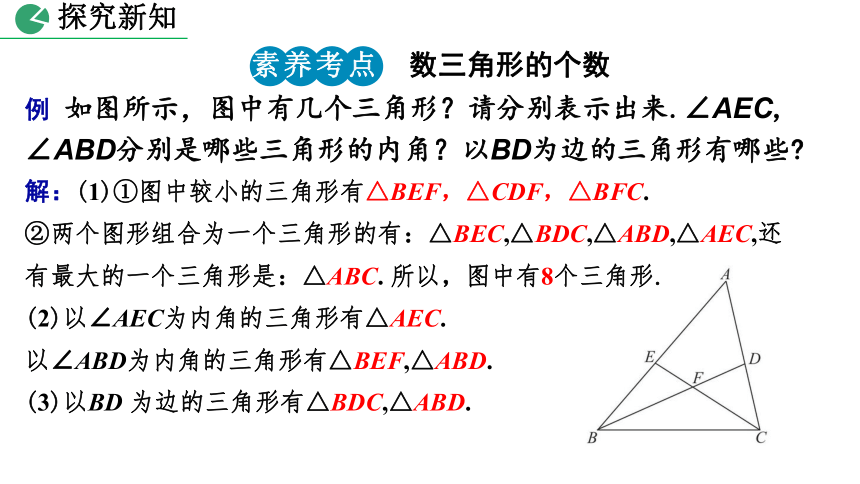
例 如图所示,图中有几个三角形?请分别表示出来.∠AEC, ∠ABD分别是哪些三角形的内角?以BD为边的三角形有哪些?
素养考点 1
数三角形的个数
解:(1)①图中较小的三角形有△BEF,△CDF,△BFC.
②两个图形组合为一个三角形的有:△BEC,△BDC,△ABD,△AEC,还有最大的一个三角形是:△ABC. 所以,图中有8个三角形.
(2)以∠AEC为内角的三角形有△AEC.
以∠ABD为内角的三角形有△BEF,△ABD.
(3)以BD 为边的三角形有△BDC,△ABD.
探究新知
复杂图形中确定三角形个数的三个要求
(1)按一定方向数:按从上到下或从左到右等一定的方向数.
(2)按从小到大的顺序数:先数单一的三角形,再数组合的三角形.
(3)不重不漏:边数边记,要做到不重复、不遗漏.
探究新知
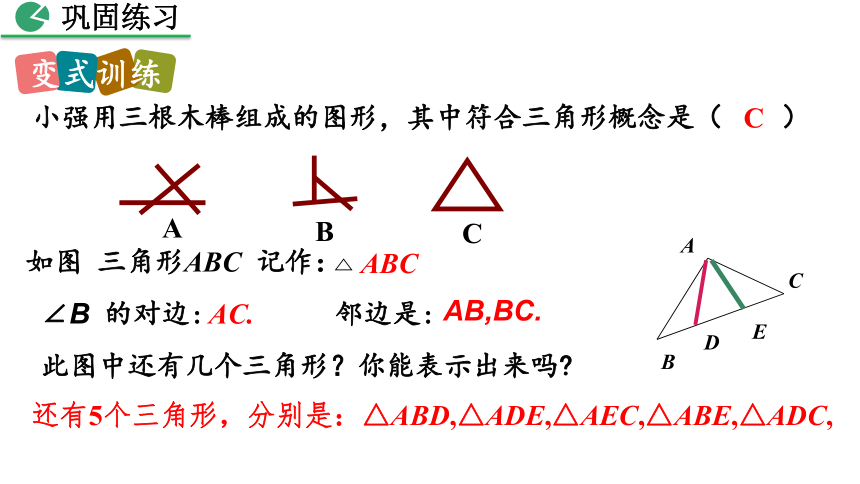
如图 三角形ABC 记作:
∠B 的对边: 邻边是:
小强用三根木棒组成的图形,其中符合三角形概念是( )
B
此图中还有几个三角形?你能表示出来吗?
A
C
ABC
AC.
AB,BC.
A
B
C
D
E
C
还有5个三角形,分别是:△ABD,△ADE,△AEC,△ABE,△ADC,
巩固练习
变式训练
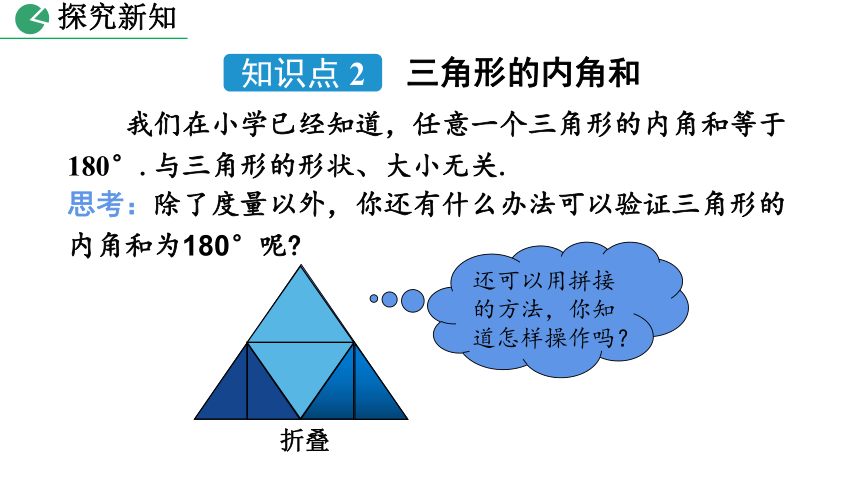
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?
折叠
还可以用拼接的方法,你知道怎样操作吗?
知识点 2
三角形的内角和
探究新知
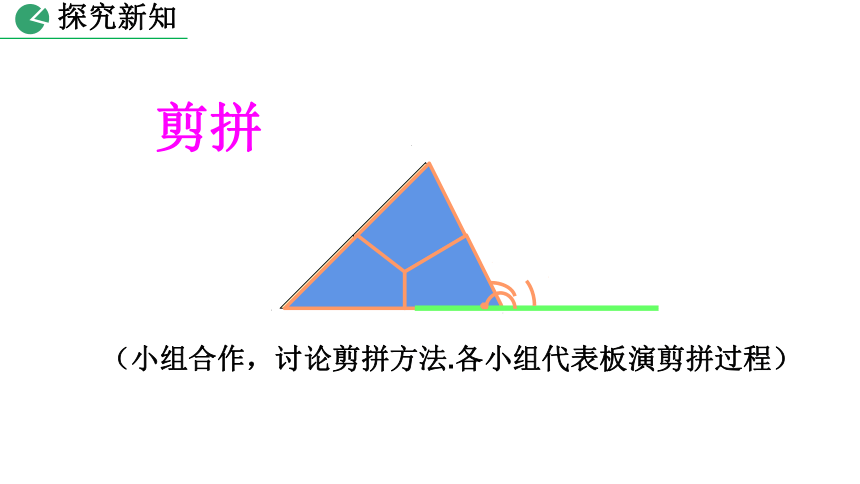
剪拼
A
B
C
2
1
(小组合作,讨论剪拼方法.各小组代表板演剪拼过程)
探究新知
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
探究新知
验证结论
三角形三个内角的和等于180°.
试说明:∠A+∠B+∠C=180°.
已知:△ABC.
方法1:过点A作l∥BC,
所以∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
因为∠2+∠1+∠BAC=180°,
所以∠B+∠C+∠BAC=180°.
1
2
探究新知
方法2:延长BC到D,过点C作CE∥BA,
所以 ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°,
所以∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
探究新知
C
B
A
E
D
F
方法3:过D作DE∥AC,作DF∥AB.
所以 ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
所以 ∠A=∠EDF.
因为∠EDB+∠EDF+∠FDC=180°,
所以∠A+∠B+∠C=180°.
探究新知
思考:多种方法说明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
探究新知
例 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, ∠BAD = ∠CAD ,求∠ADB的度数.
A
B
C
D
解:由∠BAD = ∠CAD ,得
∠BAD= ∠BAC=20 °.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°.
利用三角形的内角和定理求角的度数
素养考点 1
探究新知
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:因为∠A=50°,∠B=70°,
所以∠ACB=180°-∠A-∠B=60°.
因为CD是∠ACB的平分线,
所以∠BCD= ∠ACB=30°.
因为DE∥BC,
所以∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
巩固练习
变式训练
议一议:
(1)图1中小明所拿三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由.
(2)图2中三角形被遮住的两个内角可能是什么角?将所得结果与(1)的结果进行比较.
探究新知
知识点 3
三角形按角分类
图1
图2
小明所拿三角形被遮住的两个内角是锐角,小颖的也是锐角,因为三角形的内角和是180°,所以一个三角形内不能有两个直角或钝角.
三角形被遮住的两个内角可能是锐角,也可能一个直角和一个锐角,或一个钝角和一个锐角.
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
按三角形内角的大小把三角形分为三类
探究新知
例 在△ABC中,∠C=65°,∠B=25°,则这个三角形是 _______ .
解析:∠A=180°-∠C-∠B=180°-65°-25°=90°.故为直角三角形.
探究新知
素养考点 1
三角形分类的应用
提示:要确定三角形的类型,至少需要知道两个角的度数或两个角的和.
直角三角形
观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
巩固练习
变式训练
锐角三角形
直角三角形
钝角三角形
直角边
直角边
斜边
常用符号“Rt?ABC”来
表示直角三角形ABC.
思考: 直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余.
直角三角形
知识点 4
直角三角形的性质
探究新知
例 若一直角三角形的两个锐角的差是20°,则其较大锐角的度数是 .
解:设较大的锐角度数是x°,则较小的锐角为(90﹣x)°,
由题意得,x﹣(90﹣x)=20,
解得x=55,
即较大锐角的度数是55°.
55°
探究新知
素养考点 1
直角三角形性质的应用
直角三角形的一锐角为60°,则另一锐角为 .
解:因为直角三角形的一锐角为60°,
所以另一锐角为90°﹣60°=30°.
故答案为30°.
30°
巩固练习
变式训练
(2020?吉林)将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75°
C.65° D.60°
连接中考
B
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
课堂检测
基础巩固题
2.如图,共有三角形的个数是( )
A.3 B.4 C.5 D.6
D
课堂检测
基础巩固题
3.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
4.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
5.在△ABC中,∠A=45°,∠B比∠C大15°,则∠B=( )
A.125° B.100° C.75° D.50°
D
D
C
课堂检测
基础巩固题
6.如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
解:在△BDF中,
∠B=180°-∠BFD-∠D=180°-90°-50°=40°,
在△ACB中,∠A=40°,
故∠ACB=180°-∠A-∠B=180°-40°-40°=100°.
课堂检测
基础巩固题
如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:因为∠A+∠ADE=180°,
所以AB∥DE,
所以∠CED=∠B=78°.
又因为∠C=60°,
所以∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)
=42°.
课堂检测
能力提升题
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:因为△ABC中,∠A=60°.
所以∠ABC+∠ACB=120°.
因为BP平分∠ABC,CP平分∠ACB,
所以∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
因为∠PBC+∠PCB+∠BPC=180°,
所以∠BPC=180°-60°=120°.
课堂检测
拓广探索题
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 .
3.直角三角形的两个锐角互余.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第1课时)
北师大版 数学 七年级 下册
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新知
1.认识三角形的概念及基本要素,掌握三角形内角和等于180°.
2. 会把三角形按角分类,熟记直角三角形的性质.
素养目标
3. 会运用三角形内角和定理进行计算.
观察下面的屋顶框架图:
(1)你能从图中找出4个不同的三角形吗?
(2)这些三角形有什么共同的特点?
知识点 1
三角形的有关概念
探究新知
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形 . 三角形有三条边、三个内角和三个顶点.“三角形” 可以用符号“△”表示,如图,顶点是A,B,C 的三角形,记作“△ABC ” .
探究新知
△ABC 的三边,有时也用a,b,c 来表示.如图,顶点A所对的边BC用a表示,边AC,边 AB 分别用b,c来表示.
探究新知
边:
三角形中三边: AB,BC,AC.
如果我说三角形有三要素,你能猜出是哪三要素吗?
A
B
C
b
a
c
角:
三角形中有三个角:∠A,∠B,∠C.
顶点:
三角形中有三个顶点,顶点A,顶点B,顶点C.
探究新知
例 如图所示,图中有几个三角形?请分别表示出来.∠AEC, ∠ABD分别是哪些三角形的内角?以BD为边的三角形有哪些?
素养考点 1
数三角形的个数
解:(1)①图中较小的三角形有△BEF,△CDF,△BFC.
②两个图形组合为一个三角形的有:△BEC,△BDC,△ABD,△AEC,还有最大的一个三角形是:△ABC. 所以,图中有8个三角形.
(2)以∠AEC为内角的三角形有△AEC.
以∠ABD为内角的三角形有△BEF,△ABD.
(3)以BD 为边的三角形有△BDC,△ABD.
探究新知
复杂图形中确定三角形个数的三个要求
(1)按一定方向数:按从上到下或从左到右等一定的方向数.
(2)按从小到大的顺序数:先数单一的三角形,再数组合的三角形.
(3)不重不漏:边数边记,要做到不重复、不遗漏.
探究新知
如图 三角形ABC 记作:
∠B 的对边: 邻边是:
小强用三根木棒组成的图形,其中符合三角形概念是( )
B
此图中还有几个三角形?你能表示出来吗?
A
C
ABC
AC.
AB,BC.
A
B
C
D
E
C
还有5个三角形,分别是:△ABD,△ADE,△AEC,△ABE,△ADC,
巩固练习
变式训练
我们在小学已经知道,任意一个三角形的内角和等于180°.与三角形的形状、大小无关.
思考:除了度量以外,你还有什么办法可以验证三角形的内角和为180°呢?
折叠
还可以用拼接的方法,你知道怎样操作吗?
知识点 2
三角形的内角和
探究新知
剪拼
A
B
C
2
1
(小组合作,讨论剪拼方法.各小组代表板演剪拼过程)
探究新知
三角形的三个内角拼到一起恰好构成一个平角.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
探究新知
验证结论
三角形三个内角的和等于180°.
试说明:∠A+∠B+∠C=180°.
已知:△ABC.
方法1:过点A作l∥BC,
所以∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
因为∠2+∠1+∠BAC=180°,
所以∠B+∠C+∠BAC=180°.
1
2
探究新知
方法2:延长BC到D,过点C作CE∥BA,
所以 ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°,
所以∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
探究新知
C
B
A
E
D
F
方法3:过D作DE∥AC,作DF∥AB.
所以 ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
所以 ∠A=∠EDF.
因为∠EDB+∠EDF+∠FDC=180°,
所以∠A+∠B+∠C=180°.
探究新知
思考:多种方法说明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
A
B
C
D
E
探究新知
例 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °, ∠BAD = ∠CAD ,求∠ADB的度数.
A
B
C
D
解:由∠BAD = ∠CAD ,得
∠BAD= ∠BAC=20 °.
在△ABD中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°.
利用三角形的内角和定理求角的度数
素养考点 1
探究新知
如图,CD是∠ACB的平分线,DE∥BC,∠A=50°,∠B=70°,求∠EDC,∠BDC的度数.
解:因为∠A=50°,∠B=70°,
所以∠ACB=180°-∠A-∠B=60°.
因为CD是∠ACB的平分线,
所以∠BCD= ∠ACB=30°.
因为DE∥BC,
所以∠EDC=∠BCD=30°,
在△BDC中,∠BDC=180°-∠B-∠BCD=80°.
巩固练习
变式训练
议一议:
(1)图1中小明所拿三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由.
(2)图2中三角形被遮住的两个内角可能是什么角?将所得结果与(1)的结果进行比较.
探究新知
知识点 3
三角形按角分类
图1
图2
小明所拿三角形被遮住的两个内角是锐角,小颖的也是锐角,因为三角形的内角和是180°,所以一个三角形内不能有两个直角或钝角.
三角形被遮住的两个内角可能是锐角,也可能一个直角和一个锐角,或一个钝角和一个锐角.
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
按三角形内角的大小把三角形分为三类
探究新知
例 在△ABC中,∠C=65°,∠B=25°,则这个三角形是 _______ .
解析:∠A=180°-∠C-∠B=180°-65°-25°=90°.故为直角三角形.
探究新知
素养考点 1
三角形分类的应用
提示:要确定三角形的类型,至少需要知道两个角的度数或两个角的和.
直角三角形
观察下面的三角形,并把它们的标号填入相应图内:
锐角三角形 直角三角形 钝角三角形
③⑤
①④⑥
②⑦
巩固练习
变式训练
锐角三角形
直角三角形
钝角三角形
直角边
直角边
斜边
常用符号“Rt?ABC”来
表示直角三角形ABC.
思考: 直角三角形的两个锐角之间
有什么关系?
直角三角形的两个锐角互余.
直角三角形
知识点 4
直角三角形的性质
探究新知
例 若一直角三角形的两个锐角的差是20°,则其较大锐角的度数是 .
解:设较大的锐角度数是x°,则较小的锐角为(90﹣x)°,
由题意得,x﹣(90﹣x)=20,
解得x=55,
即较大锐角的度数是55°.
55°
探究新知
素养考点 1
直角三角形性质的应用
直角三角形的一锐角为60°,则另一锐角为 .
解:因为直角三角形的一锐角为60°,
所以另一锐角为90°﹣60°=30°.
故答案为30°.
30°
巩固练习
变式训练
(2020?吉林)将一副三角尺按如图所示的方式摆放,则∠α的大小为( )
A.85° B.75°
C.65° D.60°
连接中考
B
1.求出下列各图中的x值.
x=70
x=60
x=30
x=50
课堂检测
基础巩固题
2.如图,共有三角形的个数是( )
A.3 B.4 C.5 D.6
D
课堂检测
基础巩固题
3.在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A.等边三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
4.一个三角形三个内角的度数之比为2:3:7,这个三角形一定是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
5.在△ABC中,∠A=45°,∠B比∠C大15°,则∠B=( )
A.125° B.100° C.75° D.50°
D
D
C
课堂检测
基础巩固题
6.如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.
解:在△BDF中,
∠B=180°-∠BFD-∠D=180°-90°-50°=40°,
在△ACB中,∠A=40°,
故∠ACB=180°-∠A-∠B=180°-40°-40°=100°.
课堂检测
基础巩固题
如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
解:因为∠A+∠ADE=180°,
所以AB∥DE,
所以∠CED=∠B=78°.
又因为∠C=60°,
所以∠EDC=180°-(∠CED+∠C)
=180°-(78°+60°)
=42°.
课堂检测
能力提升题
如图,在△ABC中,BP平分∠ABC,CP平分∠ACB,若∠BAC=60°,求∠BPC的度数.
解:因为△ABC中,∠A=60°.
所以∠ABC+∠ACB=120°.
因为BP平分∠ABC,CP平分∠ACB,
所以∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
因为∠PBC+∠PCB+∠BPC=180°,
所以∠BPC=180°-60°=120°.
课堂检测
拓广探索题
1.三角形三个内角的和等于180 ? .
2.三角形按角的大小分类:
⑴锐角三角形 :三个内角都是锐角;
⑵直角三角形 :有一个内角为直角;
⑶钝角三角形 :有一个内角为钝角 .
3.直角三角形的两个锐角互余.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
