4.3 用频率估计概率 课件(共31张PPT)
文档属性
| 名称 | 4.3 用频率估计概率 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 13:25:09 | ||
图片预览










文档简介
(共31张PPT)
用频率估计概率
第4章
概率
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.理解当试验的可能结果不是有限个,或各种结果发生的可能性不相等时,一般用统计频率的方法来估计概率.
2.了解用频率估计概率的方法与列举法求概率的区别,并能够通过对事件发生频率的分析,估计事件发生的概率.
【过程与方法】
通过做抛掷硬币试验,让学生体会到为什么可以用频率来估计概率.
【情感态度】
通过本节课学习,让同学们体会到科学来源于实践的道理,激发他们动手、动脑、探究、归纳的兴趣和欲望.
【教学重点】
了解用频率估计概率的必要性和合理性.
【教学难点】
大量重复试验得到频率值的分析,对频率与概率之间关系的理解.
情境导入
问题1
抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
会出现“正面朝上”和“反面朝上”两种情况.
问题2
它们的概率是多少?
都是
.
问题3
在实际掷硬币时,会出现什么情况呢?
探究新知
(1)抛掷一枚均匀硬币400次,每隔50次,分别记录“正面朝上”和“反面朝上”的次数,汇总数据后,完成下表:
累计抛掷次数
50
100
150
200
250
300
350
400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
(2)根据上表的数据,在下图中画折线统计图表示“正面朝上”的频率.
(2)根据上表的数据,在下图中画折线统计图表示“正面朝上”的频率.
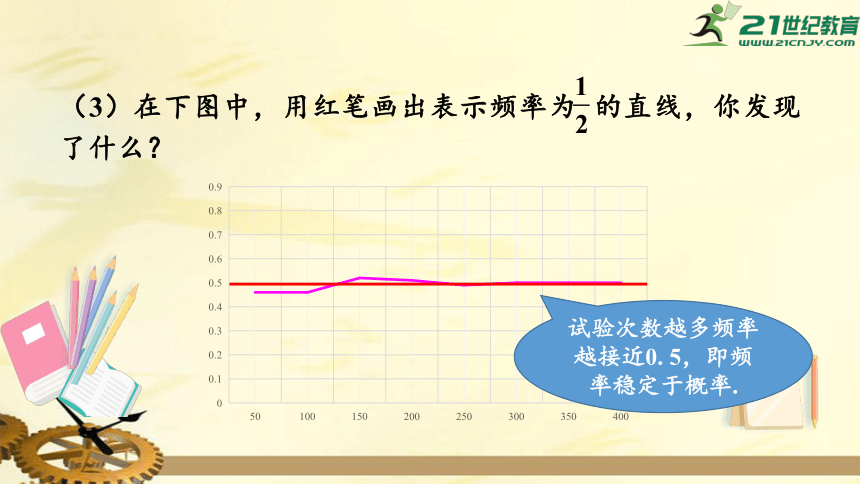
(3)在下图中,用红笔画出表示频率为
的直线,你发现了什么?
试验次数越多频率越接近0.
5,即频率稳定于概率.
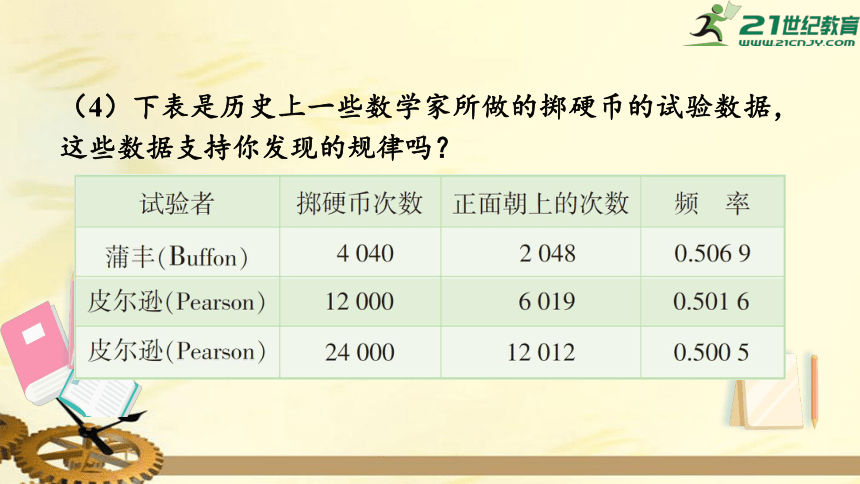
(4)下表是历史上一些数学家所做的掷硬币的试验数据,
这些数据支持你发现的规律吗?
归纳
①随着掷硬币次数的增加,“正面朝上”的频率稳定在
左右.
②通过大量的重复试验,可以用随机事件发生的频率来估计该事件发生的概率.
对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,
当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,
就不能用前面的方法来求概率.
思考:频率是否可以估计该随机事件的概率呢?
在一块平整地板上抛掷一个矿泉水瓶盖,瓶盖落地后有两种可能情况:“开口朝上”和“开口不朝上”.
由于瓶盖头重脚轻,上下不对称,“开口朝上”和“开口不朝上”
的可能性一样吗?如果不一样,出现哪种情况的可能性大一些?
我们借助重复试验来解决这个问题.
(1)全班同学分成6组,每组同学依次抛掷瓶盖80次,观察瓶盖着地时的情况,并根据全班试验结果填写下表:
累计抛掷次数
80
160
240
320
400
480
“开口朝上”的频数
“开口朝上”的频率
43
84
127
170
212
258
0.538
0.525
0.529
0.531
0.530
0.538
(2)根据上表中的数据,在下图中画折线统计图表示“开口朝上”的频率.
(2)根据上表中的数据,在下图中画折线统计图表示“开口朝上”的频率.
(3)观察下图,随着抛掷次数的增加,“开口朝上”的频率是如何变化的?
试验次数越多频率越接近0.
53,即频率稳定于概率.
(4)该试验中,是“开口朝上”的可能性大还是“开口不朝上”
的可能性大?
“开口朝上”的可能性大
归纳
在同样条件下,大量重复实验时,如果事件A发生的频率
稳定在某个常数P,那么事件A发生的概率P(A)=P.
在抛瓶盖试验中,“开口朝上”
的频率稳定于哪一个数值?
你能估计出瓶盖“开口朝上”
的概率吗?
频率与概率的区别和联系
1.频率和概率都是刻画随机事件发生可能性大小的量.
2.频率与试验次数及具体试验有关,具有随机性.
3.概率是刻画随机事件发生可能性大小的,是一个固定值,不具有随机性.
4.每次试验的可能结果不是有限个或各种可能结果发生的可能性不相等时,用频率估计概率.
瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生哪种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.
由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(2)估计这种瓷砖的合格品率(精确到0.01);
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品频率
稳定在0.962的附近,所以我们可取p=
0.96
作为该型号瓷砖的合格品率的估计.
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
500000×96%=480000(块)
可以估计该型号合格品数为480000块.
练习
如图是一个能自由转动的转盘,盘面被分成8个相同的扇形,颜色分为红、黄、蓝3
种.
转盘的指针固定,让转盘自由转动,当它停止后,记下指针指向的颜色.如此重复做50次,把结果记录在下表中:
(1)试估计当圆盘停下来时,指针指向黄色的概率是多少?
(2)如果自由转动圆盘240次,那么指针指向黄色的次数大约是多少?
随堂练习
1.关于频率与概率的关系,下列说法中正确的是(
)
A.频率等于概率
B.当试验次数很大时,频率稳定在概率的附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
B
2.在一个不透明的口袋里装着只有颜色不同的黑、白两种球共20只,某学习小组做摸球实验,每次摸完再把它放回袋中,不断重复,下表是摸球实验的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近多少?假如你摸一次,你摸到白球的概率P(白球)=________.
(2)试估算口袋中黑、白两种颜色的球分别有_______只,________只.
0.6
8
12
课堂小结
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
用频率估计概率
第4章
概率
湘教版·九年级数学下册
上课课件
学习目标
【知识与技能】
1.理解当试验的可能结果不是有限个,或各种结果发生的可能性不相等时,一般用统计频率的方法来估计概率.
2.了解用频率估计概率的方法与列举法求概率的区别,并能够通过对事件发生频率的分析,估计事件发生的概率.
【过程与方法】
通过做抛掷硬币试验,让学生体会到为什么可以用频率来估计概率.
【情感态度】
通过本节课学习,让同学们体会到科学来源于实践的道理,激发他们动手、动脑、探究、归纳的兴趣和欲望.
【教学重点】
了解用频率估计概率的必要性和合理性.
【教学难点】
大量重复试验得到频率值的分析,对频率与概率之间关系的理解.
情境导入
问题1
抛掷一枚均匀硬币,硬币落地后,会出现哪些可能的结果呢?
会出现“正面朝上”和“反面朝上”两种情况.
问题2
它们的概率是多少?
都是
.
问题3
在实际掷硬币时,会出现什么情况呢?
探究新知
(1)抛掷一枚均匀硬币400次,每隔50次,分别记录“正面朝上”和“反面朝上”的次数,汇总数据后,完成下表:
累计抛掷次数
50
100
150
200
250
300
350
400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
(2)根据上表的数据,在下图中画折线统计图表示“正面朝上”的频率.
(2)根据上表的数据,在下图中画折线统计图表示“正面朝上”的频率.
(3)在下图中,用红笔画出表示频率为
的直线,你发现了什么?
试验次数越多频率越接近0.
5,即频率稳定于概率.
(4)下表是历史上一些数学家所做的掷硬币的试验数据,
这些数据支持你发现的规律吗?
归纳
①随着掷硬币次数的增加,“正面朝上”的频率稳定在
左右.
②通过大量的重复试验,可以用随机事件发生的频率来估计该事件发生的概率.
对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,而对于一般的随机事件,
当试验所有的可能结果不是有限个,或者各种可能结果发生的可能性不相等时,
就不能用前面的方法来求概率.
思考:频率是否可以估计该随机事件的概率呢?
在一块平整地板上抛掷一个矿泉水瓶盖,瓶盖落地后有两种可能情况:“开口朝上”和“开口不朝上”.
由于瓶盖头重脚轻,上下不对称,“开口朝上”和“开口不朝上”
的可能性一样吗?如果不一样,出现哪种情况的可能性大一些?
我们借助重复试验来解决这个问题.
(1)全班同学分成6组,每组同学依次抛掷瓶盖80次,观察瓶盖着地时的情况,并根据全班试验结果填写下表:
累计抛掷次数
80
160
240
320
400
480
“开口朝上”的频数
“开口朝上”的频率
43
84
127
170
212
258
0.538
0.525
0.529
0.531
0.530
0.538
(2)根据上表中的数据,在下图中画折线统计图表示“开口朝上”的频率.
(2)根据上表中的数据,在下图中画折线统计图表示“开口朝上”的频率.
(3)观察下图,随着抛掷次数的增加,“开口朝上”的频率是如何变化的?
试验次数越多频率越接近0.
53,即频率稳定于概率.
(4)该试验中,是“开口朝上”的可能性大还是“开口不朝上”
的可能性大?
“开口朝上”的可能性大
归纳
在同样条件下,大量重复实验时,如果事件A发生的频率
稳定在某个常数P,那么事件A发生的概率P(A)=P.
在抛瓶盖试验中,“开口朝上”
的频率稳定于哪一个数值?
你能估计出瓶盖“开口朝上”
的概率吗?
频率与概率的区别和联系
1.频率和概率都是刻画随机事件发生可能性大小的量.
2.频率与试验次数及具体试验有关,具有随机性.
3.概率是刻画随机事件发生可能性大小的,是一个固定值,不具有随机性.
4.每次试验的可能结果不是有限个或各种可能结果发生的可能性不相等时,用频率估计概率.
瓷砖生产受烧制时间、温度、材质的影响,一块砖坯放在炉中烧制,可能成为合格品,也可能成为次品或废品,究竟发生哪种结果,在烧制前无法预知,所以这是一种随机现象.而烧制的结果是“合格品”是一个随机事件,这个事件的概率称为“合格品率”.
由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(1)计算上表中合格品率的各频率(精确到0.001);
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(2)估计这种瓷砖的合格品率(精确到0.01);
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
观察上表,可以发现,当抽取的瓷砖数n≥400时,合格品频率
稳定在0.962的附近,所以我们可取p=
0.96
作为该型号瓷砖的合格品率的估计.
抽取瓷砖数n
100
200
300
400
500
600
800
1000
2000
合格品数m
95
192
287
385
481
577
770
961
1924
合格品率
(3)若该厂本月生产该型号瓷砖500000块,试估计合格品数.
0.950
0.960
0.957
0.963
0.962
0.962
0.963
0.961
0.962
500000×96%=480000(块)
可以估计该型号合格品数为480000块.
练习
如图是一个能自由转动的转盘,盘面被分成8个相同的扇形,颜色分为红、黄、蓝3
种.
转盘的指针固定,让转盘自由转动,当它停止后,记下指针指向的颜色.如此重复做50次,把结果记录在下表中:
(1)试估计当圆盘停下来时,指针指向黄色的概率是多少?
(2)如果自由转动圆盘240次,那么指针指向黄色的次数大约是多少?
随堂练习
1.关于频率与概率的关系,下列说法中正确的是(
)
A.频率等于概率
B.当试验次数很大时,频率稳定在概率的附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
B
2.在一个不透明的口袋里装着只有颜色不同的黑、白两种球共20只,某学习小组做摸球实验,每次摸完再把它放回袋中,不断重复,下表是摸球实验的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近多少?假如你摸一次,你摸到白球的概率P(白球)=________.
(2)试估算口袋中黑、白两种颜色的球分别有_______只,________只.
0.6
8
12
课堂小结
1.用频率估计概率的条件及方法,应用以上的内容解决一些实际问题.
2.从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,立即可以发现:在大量的偶然之中存在着必然的规律.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
