抛物线及其标准方程
图片预览






文档简介
(共29张PPT)
抛物线及其标准方程
生活中存在着各种形式的抛物线
我们对抛物线已有了哪些认识?
y
x
o
二次函数是开口向上或向下的抛物线。
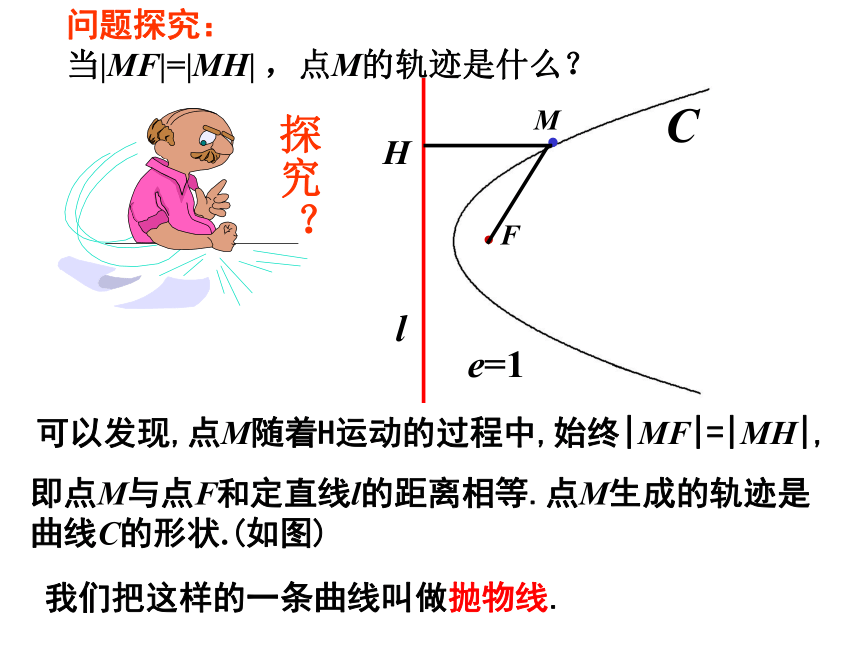
问题探究:
当|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
M
·
F
l
·
e=1
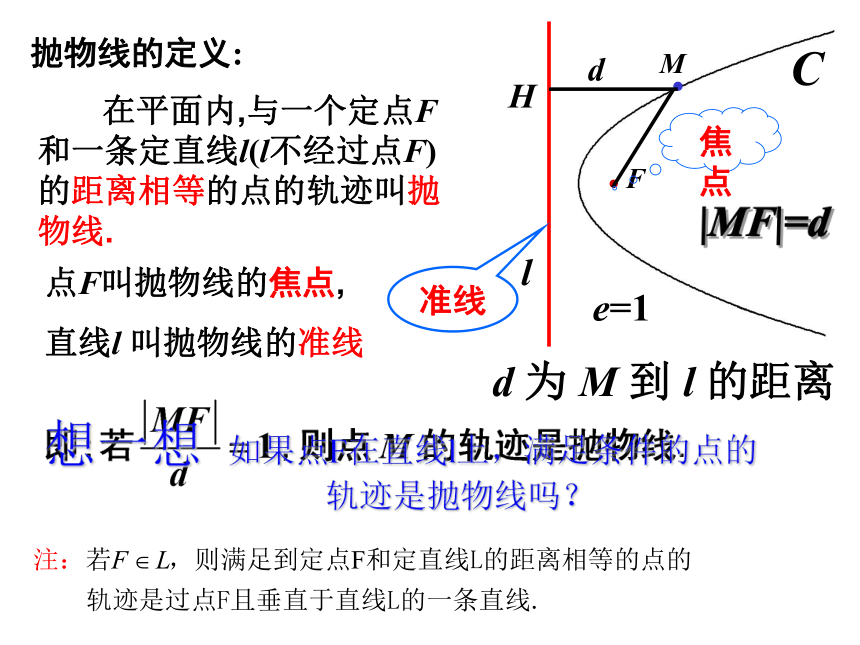
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
d 为 M 到 l 的距离
准线
焦点
d
抛物线的定义:
想一想 如果点F在直线l上,满足条件的点的
轨迹是抛物线吗?
如何建立直角坐标系?
想一想
探索研究 推出方程
求曲线方程的基本步骤
·
F
L
.
F
M
.
抛物线的标准方程:
设|FK|=p(p>0),M(x,y)
由抛物线定义知:|MF|=d
即:
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
说明:
焦点到准线的距离.
x
它所表示的抛物线的焦点F在 x 轴的正半轴上,坐标是( ),它的
准线方程是 .
y
o
L
F
p的几何意义:
已知抛物线的标准方程,
求其焦点坐标和准线方程.
标准方程 焦点坐标 准线方程
巩固练习1
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
x
y
o
L
F
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
想一想:
抛物线的位置及其方程还有没有其它的形式?
F
l
F
l
F
l
F
l
问题:仿照前面求抛物线标准方程的方法,你能建立适当的坐标系,求下列后三幅图中抛物线的方程吗
(1)
(2)
(3)
(4)
图
形
焦点位置
标准方程
焦点坐标
准线方程
不同位置的抛物线标准方程
x轴的
正方向
x轴的
负方向
y轴的
正方向
y轴的
负方向
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
(P>0)
抛物线方程
左右型
标准方程为
y2 =±2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =±2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
抛物线的标准方程
上下型
1、一次项的变量如为x(或y),
则x轴(或y轴)为抛物线的对
称轴,焦点就在对称轴上。
2、一次项的系数符号决定了开
口方向。
【小结】
▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口
椭 圆:看分母大小
双曲线:看符号
P58思考:
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
*
例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
解: ∵2P=6,∴P=3
∴抛物线的焦点坐标是( ,0)
准线方程是x=
是一次项系数的
是一次项系数的
的相反数
*
例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,
所以设所求的标准方程为x2= -2py
由题意得 , 即p=4
∴所求的标准方程为x2= -8y
(课本59页练习1)根据下列条件写出抛物线的标准方程;
(1)焦点是(3,0);
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
y2=12x
y2=x
y2=4x
y2=-4x
x2=4y
x2=-4y
F(5,0)
F(0,-2)
x=-5
y=2
y=-
(课本59页练习2)求下列抛物线的焦点坐标和准线方程:
(1)y2=20x
(2)x2= y
(3)2y2+5x=0
(4)x2+8y=0
F(0, )
x=
F(- ,0)
练习:课本59页练习3
小 结 :
1、学习好一个概念--抛物线
2、掌握好一种题型--
3、注重好一种思想--数形结合
有关抛物线的标准方程和它的焦点坐标、准线方程的求法
抛物线及其标准方程
生活中存在着各种形式的抛物线
我们对抛物线已有了哪些认识?
y
x
o
二次函数是开口向上或向下的抛物线。
问题探究:
当|MF|=|MH| ,点M的轨迹是什么?
探究?
可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)
M
·
F
l
·
e=1
我们把这样的一条曲线叫做抛物线.
M
·
F
l
·
e=1
在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.
点F叫抛物线的焦点,
直线l 叫抛物线的准线
d 为 M 到 l 的距离
准线
焦点
d
抛物线的定义:
想一想 如果点F在直线l上,满足条件的点的
轨迹是抛物线吗?
如何建立直角坐标系?
想一想
探索研究 推出方程
求曲线方程的基本步骤
·
F
L
.
F
M
.
抛物线的标准方程:
设|FK|=p(p>0),M(x,y)
由抛物线定义知:|MF|=d
即:
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
说明:
焦点到准线的距离.
x
它所表示的抛物线的焦点F在 x 轴的正半轴上,坐标是( ),它的
准线方程是 .
y
o
L
F
p的几何意义:
已知抛物线的标准方程,
求其焦点坐标和准线方程.
标准方程 焦点坐标 准线方程
巩固练习1
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
x
y
o
L
F
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.
想一想:
抛物线的位置及其方程还有没有其它的形式?
F
l
F
l
F
l
F
l
问题:仿照前面求抛物线标准方程的方法,你能建立适当的坐标系,求下列后三幅图中抛物线的方程吗
(1)
(2)
(3)
(4)
图
形
焦点位置
标准方程
焦点坐标
准线方程
不同位置的抛物线标准方程
x轴的
正方向
x轴的
负方向
y轴的
正方向
y轴的
负方向
y2=2px
y2=-2px
x2=2py
x2=-2py
F(-
-
-
-
(P>0)
抛物线方程
左右型
标准方程为
y2 =±2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =±2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
抛物线的标准方程
上下型
1、一次项的变量如为x(或y),
则x轴(或y轴)为抛物线的对
称轴,焦点就在对称轴上。
2、一次项的系数符号决定了开
口方向。
【小结】
▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口
椭 圆:看分母大小
双曲线:看符号
P58思考:
二次函数 的图像为什么是抛物线?
当a>0时与当a<0时,结论都为:
*
例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;
解: ∵2P=6,∴P=3
∴抛物线的焦点坐标是( ,0)
准线方程是x=
是一次项系数的
是一次项系数的
的相反数
*
例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程。
解: 因为焦点在y的负半轴上,
所以设所求的标准方程为x2= -2py
由题意得 , 即p=4
∴所求的标准方程为x2= -8y
(课本59页练习1)根据下列条件写出抛物线的标准方程;
(1)焦点是(3,0);
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
y2=12x
y2=x
y2=4x
y2=-4x
x2=4y
x2=-4y
F(5,0)
F(0,-2)
x=-5
y=2
y=-
(课本59页练习2)求下列抛物线的焦点坐标和准线方程:
(1)y2=20x
(2)x2= y
(3)2y2+5x=0
(4)x2+8y=0
F(0, )
x=
F(- ,0)
练习:课本59页练习3
小 结 :
1、学习好一个概念--抛物线
2、掌握好一种题型--
3、注重好一种思想--数形结合
有关抛物线的标准方程和它的焦点坐标、准线方程的求法
