2020--2021学年北师大版七年级数学下册5.3 简单的轴对称图形(第3课时)课件(共27张)
文档属性
| 名称 | 2020--2021学年北师大版七年级数学下册5.3 简单的轴对称图形(第3课时)课件(共27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 637.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 13:47:20 | ||
图片预览





文档简介
5.3 简单的轴对称图形
(第3课时)
北师大版 数学 七年级 下册
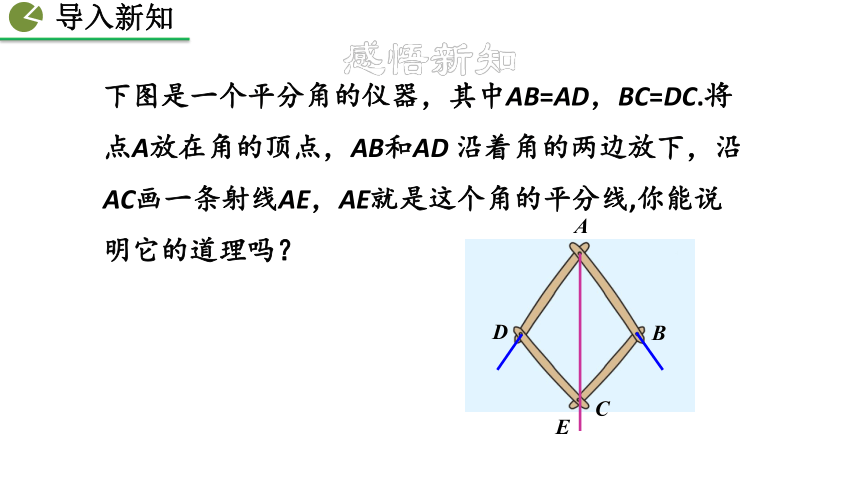
A
B
D
C
E
下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD 沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,你能说明它的道理吗?
导入新知
1. 通过操作、验证等方式,探究并掌握角平分线的性质.
2. 学会角平分线的画法.
素养目标
3. 能运用角的平分线性质解决简单的几何问题.
做一做:
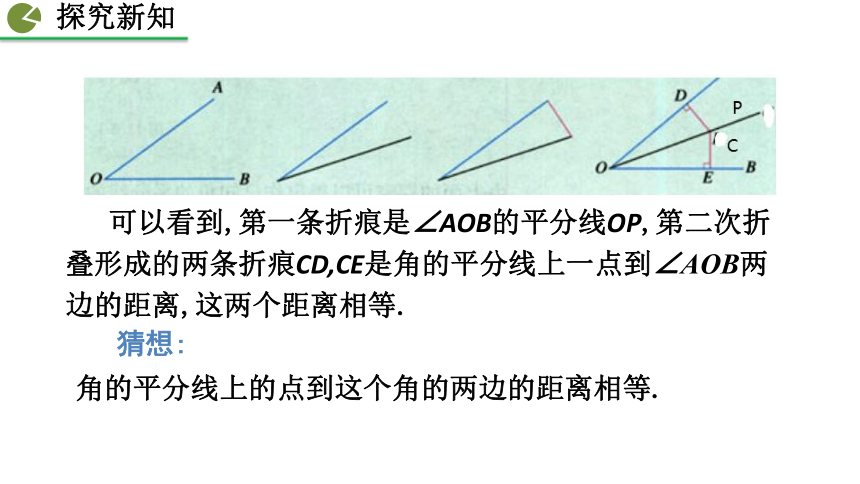
(1)在一张纸上任意画∠AOB,沿角的两边将角剪下,将这个角对折,使角的两边重合;
(2)在折痕(即角平分线)上任意取一点C,过点C分别向∠AOB的两边折垂线,垂足分别为D,E,将∠AOB再次对折,折痕CD与CE能重合吗?
改变点C的位置,CD和CE还相等吗?
知识点 1
角平分线的性质
探究新知
猜想:
可以看到,第一条折痕是∠AOB的平分线OP,第二次折叠形成的两条折痕CD,CE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.
角的平分线上的点到这个角的两边的距离相等.
探究新知
验证猜想
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
试说明:PD=PE.
C
A
O
B
P
D
E
解:
因为 PD⊥OA,PE⊥OB,
所以 ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
所以△PDO ≌△PEO(AAS).
所以PD=PE.
探究新知
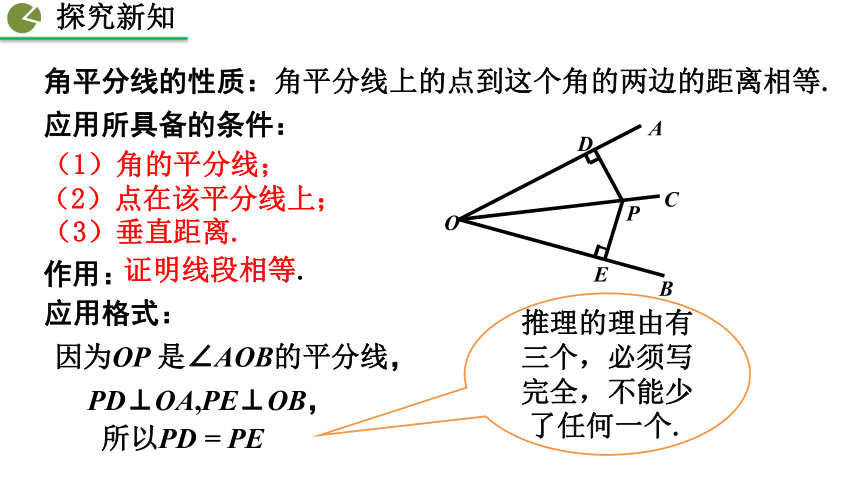
角平分线的性质:角平分线上的点到这个角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
作用:
证明线段相等.
应用格式:
因为OP 是∠AOB的平分线,
所以PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
探究新知
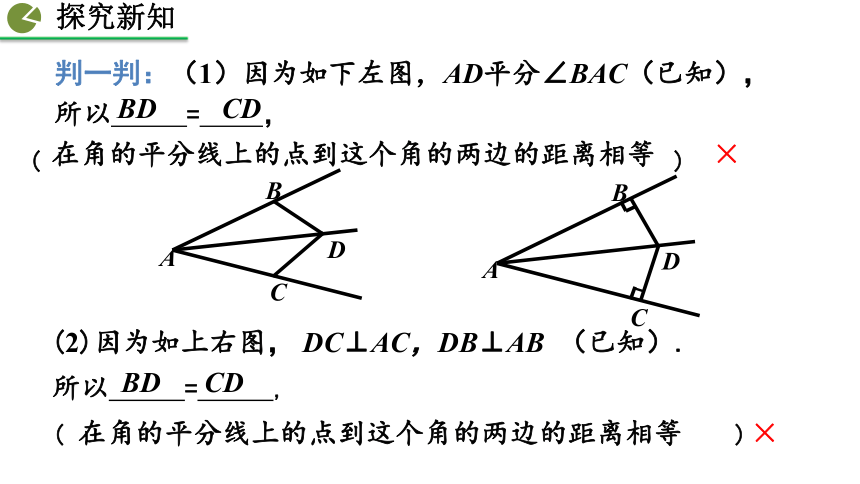
判一判:(1)因为如下左图,AD平分∠BAC(已知),
所以 = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)因为如上右图, DC⊥AC,DB⊥AB (已知).
所以 = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
探究新知
例1 已知:如图,在△ABC中,AD是它的角平分线,且∠ B= ∠ C,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: 因为AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
所以 DE=DF, ∠DEB=∠DFC=90 °.
在△BDE 和 △CDF中,
所以△BDE ≌ △CDF(AAS).
所以EB=FC.
角平分线的性质的应用
素养考点 1
∠ B= ∠C ,
DE=DF ,
∠DEB=∠DFC
探究新知
如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.试说明:PM=PN.
解:因为OD平分∠AOB,∠1=∠2,
又因为OA=OB,OD=OD,
所以△AOD≌△BOD,所以∠3=∠4,
又因为PM⊥DB,PN⊥DA,
所以PM=PN(角平分线上的点到角两边的距离相等).
巩固练习
变式训练
例2 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,
PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
探究新知
利用角平分线的性质求线段的长度
素养考点 2
解析:因为AM 是∠BAC的平分线,
PD⊥OB,PE⊥OC,
所以PD = PE=4
A
B
C
P
如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
则点P到AB的距离为_______.
D
4
巩固练习
变式训练
探究1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
探究2:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
探究新知
知识点 2
角平分线的画法
探究3:如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
探究新知
解: 在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
所以 △ACD≌ △ACB(SSS)
所以∠CAD=∠CAB(全等三角形的对应边相等)
所以AE平分∠DAB(角平分线的定义)
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
探究新知
探究4:如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
利用尺规,作∠AOB的平分线.
已知:∠AOB.
求作:射线 OC,使∠AOC =∠BOC.
探究新知
2.分别以D,E为圆心.大于 DE的长为半径作弧.两弧在∠AOB的内部交于C.
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
3.作射线OC.
OC就是∠AOB的平分线.
O
B
A
C
E
D
探究新知
先任意画一个角,然后将它四等分.
作法:画出已知角∠AOB .
1.作∠AOB 的平分线OC.
2.分别作∠AOC和∠BOC的平分线OD、OE,即将∠AOB四等分 .
O
B
A
C
E
D
巩固练习
(2020?怀化)在Rt△ABC中,∠B=90°,AD平分∠BAC,
交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A.3 B.1.5 C.2 D.6
连接中考
A
1.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
基础巩固题
课堂检测
2.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA C.AAS
D.角平分线上的点到角两
边的距离相等
A
B
M
N
C
O
A
课堂检测
基础巩固题
3. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
解析:过点D作DF⊥AC于F,
因为AD是△ABC的角平分线,
DE⊥AB,
所以DF=DE=2,
解得AC=3.
课堂检测
基础巩固题
4.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.
解:(1)DC=DE.理由如下:角平分线上的点到角两边的距离相等.
(2)因为BD平分∠ABC ,所以∠ABD= ∠DBC
在△CDB和△EDB中,
DC=DE, ∠BED= ∠DCB , ∠ABD= ∠DBC
所以△CDB≌△EDB(AAS),
所以BE=BC=8.
所以AE=AB-BE=2.
所以△AED的周长=AE+ED+DA=2+6=8.
E
D
C
B
A
8
10
C
D
课堂检测
基础巩固题
如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.试说明:CE=CF.
解:因为CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
所以DE=DF, ∠DCE= ∠DCF, ∠DEC= ∠DFC.
所以△CDE≌△CDF(AAS),
所以CE=CF.
课堂检测
能力提升题
如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
因为 AD∥BC,
所以 MN⊥BC,MN的长即为AD与BC之间的距离.
因为AP平分∠BAD, PM⊥AD , PE⊥AB,
所以PM= PE.
同理, PN= PE.
所以PM= PN= PE=3.
所以MN=6.即AD与BC之间的距离为6.
课堂检测
拓广探索题
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
(第3课时)
北师大版 数学 七年级 下册
A
B
D
C
E
下图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD 沿着角的两边放下,沿AC画一条射线AE,AE就是这个角的平分线,你能说明它的道理吗?
导入新知
1. 通过操作、验证等方式,探究并掌握角平分线的性质.
2. 学会角平分线的画法.
素养目标
3. 能运用角的平分线性质解决简单的几何问题.
做一做:
(1)在一张纸上任意画∠AOB,沿角的两边将角剪下,将这个角对折,使角的两边重合;
(2)在折痕(即角平分线)上任意取一点C,过点C分别向∠AOB的两边折垂线,垂足分别为D,E,将∠AOB再次对折,折痕CD与CE能重合吗?
改变点C的位置,CD和CE还相等吗?
知识点 1
角平分线的性质
探究新知
猜想:
可以看到,第一条折痕是∠AOB的平分线OP,第二次折叠形成的两条折痕CD,CE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.
角的平分线上的点到这个角的两边的距离相等.
探究新知
验证猜想
已知:如图, ∠AOC= ∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
试说明:PD=PE.
C
A
O
B
P
D
E
解:
因为 PD⊥OA,PE⊥OB,
所以 ∠PDO= ∠PEO=90 °.
在△PDO和△PEO中,
∠PDO= ∠PEO,
∠AOC= ∠BOC,
OP= OP,
所以△PDO ≌△PEO(AAS).
所以PD=PE.
探究新知
角平分线的性质:角平分线上的点到这个角的两边的距离相等.
应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
作用:
证明线段相等.
应用格式:
因为OP 是∠AOB的平分线,
所以PD = PE
推理的理由有三个,必须写完全,不能少了任何一个.
PD⊥OA,PE⊥OB,
B
A
D
O
P
E
C
探究新知
判一判:(1)因为如下左图,AD平分∠BAC(已知),
所以 = ,( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
(2)因为如上右图, DC⊥AC,DB⊥AB (已知).
所以 = ,
( )
在角的平分线上的点到这个角的两边的距离相等
BD CD
×
B
A
D
C
探究新知
例1 已知:如图,在△ABC中,AD是它的角平分线,且∠ B= ∠ C,DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: 因为AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
所以 DE=DF, ∠DEB=∠DFC=90 °.
在△BDE 和 △CDF中,
所以△BDE ≌ △CDF(AAS).
所以EB=FC.
角平分线的性质的应用
素养考点 1
∠ B= ∠C ,
DE=DF ,
∠DEB=∠DFC
探究新知
如图,已知:OD平分∠AOB,在OA,OB边上取OA=OB,PM⊥BD,PN⊥AD,垂足分别为M,N.试说明:PM=PN.
解:因为OD平分∠AOB,∠1=∠2,
又因为OA=OB,OD=OD,
所以△AOD≌△BOD,所以∠3=∠4,
又因为PM⊥DB,PN⊥DA,
所以PM=PN(角平分线上的点到角两边的距离相等).
巩固练习
变式训练
例2 如图,AM是∠BAC的平分线,点P在AM上,PD⊥AB,PE⊥AC,垂足分别是D、E,
PD=4cm,则PE=______cm.
B
A
C
P
M
D
E
4
探究新知
利用角平分线的性质求线段的长度
素养考点 2
解析:因为AM 是∠BAC的平分线,
PD⊥OB,PE⊥OC,
所以PD = PE=4
A
B
C
P
如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
则点P到AB的距离为_______.
D
4
巩固练习
变式训练
探究1:在纸上画一个角,你能得到这个角的平分线吗?
用量角器度量,也可用折纸的方法.
探究2:如果把前面的纸片换成木板、钢板等,还能用对折的方法得到木板、钢板的角平分线吗?
探究新知
知识点 2
角平分线的画法
探究3:如图,是一个角平分仪,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
B
C
(E)
D
探究新知
解: 在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
所以 △ACD≌ △ACB(SSS)
所以∠CAD=∠CAB(全等三角形的对应边相等)
所以AE平分∠DAB(角平分线的定义)
A
B
M
N
C
O
已知:∠AOB.
求作:∠AOB的平分线.
作法:
(1)以点O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点MN为圆心,大于 MN的长为半径画弧,两弧在∠AOB的内部相交于点C.
(3)画射线OC.射线OC即为所求.
探究新知
探究4:如果没有此仪器,我们用数学作图工具,能实现该仪器的功能吗?
利用尺规,作∠AOB的平分线.
已知:∠AOB.
求作:射线 OC,使∠AOC =∠BOC.
探究新知
2.分别以D,E为圆心.大于 DE的长为半径作弧.两弧在∠AOB的内部交于C.
作法:
1.在OA和OB上分别截取OD,OE,使OD=OE.
3.作射线OC.
OC就是∠AOB的平分线.
O
B
A
C
E
D
探究新知
先任意画一个角,然后将它四等分.
作法:画出已知角∠AOB .
1.作∠AOB 的平分线OC.
2.分别作∠AOC和∠BOC的平分线OD、OE,即将∠AOB四等分 .
O
B
A
C
E
D
巩固练习
(2020?怀化)在Rt△ABC中,∠B=90°,AD平分∠BAC,
交BC于点D,DE⊥AC,垂足为点E,若BD=3,则DE的长为( )
A.3 B.1.5 C.2 D.6
连接中考
A
1.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
A
B
C
D
3
E
基础巩固题
课堂检测
2.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA C.AAS
D.角平分线上的点到角两
边的距离相等
A
B
M
N
C
O
A
课堂检测
基础巩固题
3. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,S△ABC=7,DE=2,AB=4,则AC的长是( )
A.6 B.5 C.4 D.3
D
B
C
E
A
D
F
解析:过点D作DF⊥AC于F,
因为AD是△ABC的角平分线,
DE⊥AB,
所以DF=DE=2,
解得AC=3.
课堂检测
基础巩固题
4.在Rt△ABC中,BD平分∠ABC,DE⊥AB于E,则:
(1)哪条线段与DE相等?为什么?
(2)若AB=10,BC=8,AC=6,求BE,AE的长和△AED的周长.
解:(1)DC=DE.理由如下:角平分线上的点到角两边的距离相等.
(2)因为BD平分∠ABC ,所以∠ABD= ∠DBC
在△CDB和△EDB中,
DC=DE, ∠BED= ∠DCB , ∠ABD= ∠DBC
所以△CDB≌△EDB(AAS),
所以BE=BC=8.
所以AE=AB-BE=2.
所以△AED的周长=AE+ED+DA=2+6=8.
E
D
C
B
A
8
10
C
D
课堂检测
基础巩固题
如图所示,D是∠ACG的平分线上的一点.DE⊥AC,DF⊥CG,垂足分别为E,F.试说明:CE=CF.
解:因为CD是∠ACG的平分线,DE⊥AC,DF⊥CG,
所以DE=DF, ∠DCE= ∠DCF, ∠DEC= ∠DFC.
所以△CDE≌△CDF(AAS),
所以CE=CF.
课堂检测
能力提升题
如图,已知AD∥BC,P是∠BAD与∠ABC的平分线的交点,PE⊥AB于E,且PE=3,求AD与BC之间的距离.
解:过点P作MN⊥AD于点M,交BC于点N.
因为 AD∥BC,
所以 MN⊥BC,MN的长即为AD与BC之间的距离.
因为AP平分∠BAD, PM⊥AD , PE⊥AB,
所以PM= PE.
同理, PN= PE.
所以PM= PN= PE=3.
所以MN=6.即AD与BC之间的距离为6.
课堂检测
拓广探索题
角平分线
尺规作图
属于基本作图,必须熟练掌握
性质
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
