2020--2021学年北师大版七年级数学下册1.5 平方差公式(第2课时)课件(共20张)
文档属性
| 名称 | 2020--2021学年北师大版七年级数学下册1.5 平方差公式(第2课时)课件(共20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 258.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-08 14:23:18 | ||
图片预览







文档简介
北师大版 数学 七年级 下册
1.5 平方差公式(第2课时)
某同学在计算97×103时将其变成(100-3)(100+3)
并很快得出结果,你知道他运用了什么知识吗?这节
课我们一起来探讨上述计算的规律.
导入新知
1. 灵活地运用平方差公式进行简便计算.
2. 了解平方差公式的几何意义,体会数形结合的思想方法.
素养目标
3. 利用平方差公式解答简单问题.
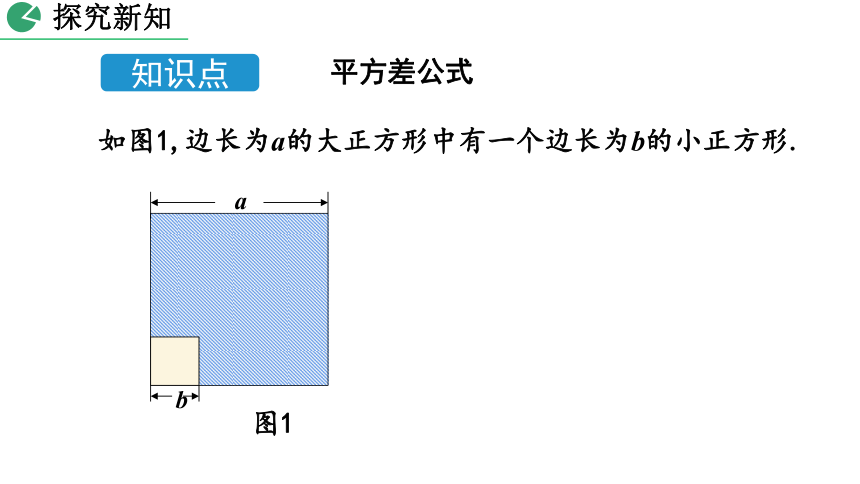
如图1,边长为a的大正方形中有一个边长为b的小正方形.
a
b
探究新知
知识点
平方差公式
图1
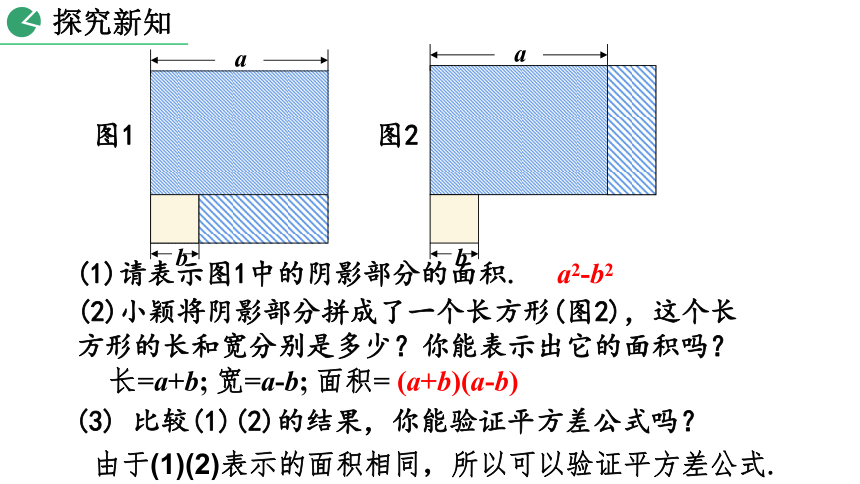
(1)请表示图1中的阴影部分的面积.
(2)小颖将阴影部分拼成了一个长方形(图2),这个长方形的长和宽分别是多少?你能表示出它的面积吗?
a2-b2
长=a+b; 宽=a-b; 面积= (a+b)(a-b)
(3) 比较(1)(2)的结果,你能验证平方差公式吗?
由于(1)(2)表示的面积相同,所以可以验证平方差公式.
探究新知
a
b
a
b
图1
图2
(1)计算下列各组算式,并观察它们的共同特点.
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
63
64
143
144
639
640
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
(a-1) (a+1) = a2 – 1 平方差公式
探究新知
解: (1) 103×97
=(100+3)(100-3)
=1002-32
=9991
(2)118×122
=(120-2)(120+2)
=1202-22
=14396
(1) 103×97; (2)118×122
探究新知
用平方差公式进行计算:
例1
通过合理变形,利用平方差公式,可以简化运算.
素养考点 1
利用平方差公式进行简便运算
解: (1) 102×98
= 1002-22
=10000 – 4
=(100+2)(100-2)
=9996;
计算:
(1) 102×98;
(2) 51×49;
(2) 原式=(50+1)(50-1)
= 502-12
=2500 – 1
=2499;
巩固练习
变式训练
探究新知
计算:
(1)a2 (a+b)(a-b)+a2 b2
(2)(2x-5)(2x+5)-2x(2x-3)
例2
解: (1)a2 (a+b)(a-b)+a2 b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)(2x-5)(2x+5)-2x(2x-3)
=4x2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
素养考点 2
平方差公式在混合运算中的应用
计算:
(1) (3x+4)(3x-4)-(2x+3)(3x-2)
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 原式=(3x)2-42-(6x2+5x-6)
(2)原式= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
巩固练习
变式训练
例3 对于任意的正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n-1)-(3-n)(3+n)的值是10的倍数.
解:原式=9n2-1-(9-n2)
=10n2-10.
因为(10n2-10)÷10=n2-1.
n为正整数,
所以n2-1为整数
探究新知
利用平方差公式进行证明
素养考点 3
方法总结:在探究整除性或倍数问题时,一般先将代数式化为最简,然后根据结果的特征,判断其是否具有整除性或倍数关系.
巩固练习
如果两个连续奇数分别是2n-1,2n+1(其中n为正整数),证明两个连续奇数的平方差是8的倍数.
证明:(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2
=8n
因为8n是8的倍数,所以结论成立.
变式训练
注意:逆用了平方差公式奥!
(2020?郴州)如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A.x2﹣2x+1=(x-1)2 B.x2-1=(x+1)(x-1)
C.x2+2x+1=(x+1)2 D.x2-x=x(x-1)
连接中考
B
1.如图,在边长为a的正方形中裁掉一个边长为b的小正方形(如图1),将剩余部分沿虚线剪开后拼接(如图2),通过计算,用拼接前后两个图形中阴影部分的面积可以验证等式( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a+2b)(a-b)=a2+ab-2b2
D.(a-b)2=a2-2ab+b2
A
基础巩固题
课堂检测
2.计算a2-(a+1)(a-1)的结果是( )
A.1 B.-1 C.2a2+1 D.2a2-1
A
3.计算20202-2019×2021=____.
1
4.已知a-b=1,a+b=2021,则a2-b2的值为_____.
2021
课堂检测
基础巩固题
5.计算: 20152 - 2014×2016.
解:
20152 - 2014×2016
= 20152 - (2015-1)(2015+1)
= 20152
- (20152-12 )
= 20152
- 20152+12
=1
课堂检测
基础巩固题
对于任意一个正整数n,整式A=(4n+1)·(4n-1)-(n+1)·(n-1)能被15整除吗?请说明理由.
解:能.理由如下:
A=(4n)2-1-(n2-1)=16n2-1-n2+1=15n2.
因为n是正整数,所以15n2一定能被15整除.
课堂检测
能力提升题
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
因为a2>a2-16,
解:李大妈吃亏了.
理由:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16,
所以李大妈吃亏了.
课堂检测
拓广探索题
平方差公式的应用及注意事项
两个应用
四点注意
1.利用平方差公式简化一些数字计算.
2.逆用平方差公式进行化简、计算.
1.必须符合平方差公式的结构特征.
2.有些式子虽然不能直接应用公式,但经过适当变形或变换符号后可以运用公式进行化简、计算.
3.计算结果一定要注意字母的系数,指数的变化.
4.在运算过程中,有时可以反复应用公式.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
1.5 平方差公式(第2课时)
某同学在计算97×103时将其变成(100-3)(100+3)
并很快得出结果,你知道他运用了什么知识吗?这节
课我们一起来探讨上述计算的规律.
导入新知
1. 灵活地运用平方差公式进行简便计算.
2. 了解平方差公式的几何意义,体会数形结合的思想方法.
素养目标
3. 利用平方差公式解答简单问题.
如图1,边长为a的大正方形中有一个边长为b的小正方形.
a
b
探究新知
知识点
平方差公式
图1
(1)请表示图1中的阴影部分的面积.
(2)小颖将阴影部分拼成了一个长方形(图2),这个长方形的长和宽分别是多少?你能表示出它的面积吗?
a2-b2
长=a+b; 宽=a-b; 面积= (a+b)(a-b)
(3) 比较(1)(2)的结果,你能验证平方差公式吗?
由于(1)(2)表示的面积相同,所以可以验证平方差公式.
探究新知
a
b
a
b
图1
图2
(1)计算下列各组算式,并观察它们的共同特点.
7×9=
8×8=
11×13=
12×12=
79×81=
80×80=
63
64
143
144
639
640
(2)从以上的过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
(a-1) (a+1) = a2 – 1 平方差公式
探究新知
解: (1) 103×97
=(100+3)(100-3)
=1002-32
=9991
(2)118×122
=(120-2)(120+2)
=1202-22
=14396
(1) 103×97; (2)118×122
探究新知
用平方差公式进行计算:
例1
通过合理变形,利用平方差公式,可以简化运算.
素养考点 1
利用平方差公式进行简便运算
解: (1) 102×98
= 1002-22
=10000 – 4
=(100+2)(100-2)
=9996;
计算:
(1) 102×98;
(2) 51×49;
(2) 原式=(50+1)(50-1)
= 502-12
=2500 – 1
=2499;
巩固练习
变式训练
探究新知
计算:
(1)a2 (a+b)(a-b)+a2 b2
(2)(2x-5)(2x+5)-2x(2x-3)
例2
解: (1)a2 (a+b)(a-b)+a2 b2
=a2(a2-b2)+a2b2
=a4-a2b2+a2b2
=a4
(2)(2x-5)(2x+5)-2x(2x-3)
=4x2-52-(4x2-6x)
=4x2-25-4x2+6x
=6x-25
不符合平方差公式运算条件的乘法,按乘法法则进行运算.
素养考点 2
平方差公式在混合运算中的应用
计算:
(1) (3x+4)(3x-4)-(2x+3)(3x-2)
(2) (y+2) (y-2) – (y-1) (y+5) .
解: (1) 原式=(3x)2-42-(6x2+5x-6)
(2)原式= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
= 9x2-16-6x2-5x+6
= 3x2-5x-10.
巩固练习
变式训练
例3 对于任意的正整数n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是10的整数倍吗?
即(3n+1)(3n-1)-(3-n)(3+n)的值是10的倍数.
解:原式=9n2-1-(9-n2)
=10n2-10.
因为(10n2-10)÷10=n2-1.
n为正整数,
所以n2-1为整数
探究新知
利用平方差公式进行证明
素养考点 3
方法总结:在探究整除性或倍数问题时,一般先将代数式化为最简,然后根据结果的特征,判断其是否具有整除性或倍数关系.
巩固练习
如果两个连续奇数分别是2n-1,2n+1(其中n为正整数),证明两个连续奇数的平方差是8的倍数.
证明:(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=(2n+1+2n-1)(2n+1-2n+1)
=4n×2
=8n
因为8n是8的倍数,所以结论成立.
变式训练
注意:逆用了平方差公式奥!
(2020?郴州)如图1,将边长为x的大正方形剪去一个边长为1的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A.x2﹣2x+1=(x-1)2 B.x2-1=(x+1)(x-1)
C.x2+2x+1=(x+1)2 D.x2-x=x(x-1)
连接中考
B
1.如图,在边长为a的正方形中裁掉一个边长为b的小正方形(如图1),将剩余部分沿虚线剪开后拼接(如图2),通过计算,用拼接前后两个图形中阴影部分的面积可以验证等式( )
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a+2b)(a-b)=a2+ab-2b2
D.(a-b)2=a2-2ab+b2
A
基础巩固题
课堂检测
2.计算a2-(a+1)(a-1)的结果是( )
A.1 B.-1 C.2a2+1 D.2a2-1
A
3.计算20202-2019×2021=____.
1
4.已知a-b=1,a+b=2021,则a2-b2的值为_____.
2021
课堂检测
基础巩固题
5.计算: 20152 - 2014×2016.
解:
20152 - 2014×2016
= 20152 - (2015-1)(2015+1)
= 20152
- (20152-12 )
= 20152
- 20152+12
=1
课堂检测
基础巩固题
对于任意一个正整数n,整式A=(4n+1)·(4n-1)-(n+1)·(n-1)能被15整除吗?请说明理由.
解:能.理由如下:
A=(4n)2-1-(n2-1)=16n2-1-n2+1=15n2.
因为n是正整数,所以15n2一定能被15整除.
课堂检测
能力提升题
王大伯家把一块边长为a米的正方形土地租给了邻居李大妈.今年王大伯对李大妈说:“我把这块地一边减少4米,另外一边增加4米,继续租给你,你看如何?”李大妈一听,就答应了.你认为李大妈吃亏了吗?为什么?
因为a2>a2-16,
解:李大妈吃亏了.
理由:原正方形的面积为a2,
改变边长后面积为(a+4)(a-4)=a2-16,
所以李大妈吃亏了.
课堂检测
拓广探索题
平方差公式的应用及注意事项
两个应用
四点注意
1.利用平方差公式简化一些数字计算.
2.逆用平方差公式进行化简、计算.
1.必须符合平方差公式的结构特征.
2.有些式子虽然不能直接应用公式,但经过适当变形或变换符号后可以运用公式进行化简、计算.
3.计算结果一定要注意字母的系数,指数的变化.
4.在运算过程中,有时可以反复应用公式.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
